阿里天池大赛-工业蒸汽预测
一:赛题理解
1.1:数据说明
数据可以直接在阿里云天池官网下载。其格式如下:

上图所示为训练数据,其中V0-V37共38个特征变量,target字段是目标变量。
1.1:评估指标
预测结果以均方差MSE为评判标准:
from sklearn.metrics import mean_squared_error
mean_squared_error(y_true, y_pred)
1.2:赛题模型
在机器学习中,常用的模型包括回归预测模型和分类预测模型
1.2.1 回归预测模型
回归预测模型的预测结果是一个连续值域上的任意值,回归可以具有实值或者离散的输入变量,通常把多输入变量的回归问题称为多元回归问题,输入变量按时间排序的回归问题称为时间序列预测问题。

如上图所示,空心点为特征数据在空间的分布,其中红色直线为线性回归模型,蓝色折线为多项式回归模型。
1.2.2 分类预测模型
分类模型要求将实例分为多个(包含两个)中的一个,它具有实值或者离散的输入变量。

1.2.3 解题思路
根据提供的V0-V37共38个特征变量来预测蒸汽量的数值,其预测值为连续型数值变量,故可用回归模型求解。
回归预测模型使用的算法包括:线性回归、岭回归、LASSO回归、决策树回归、梯度提升树回归。
二:数据探索
从变量类型、数据类型等方便进行分析,可将变量分为:输入变量与输出变量、字符型数据(如职业、受教育程度)与数值型数据(年龄、每天睡眠时常)、连续型变量(速度)与类别型变量(性别)
2.1变量分析
2.1.1单变量分析
对于连续型变量一般需统计其数据的中心分布趋势和数据的总体分布。
对于类别型变量,一般使用频次或者占比表示每个类别的分布情况,对应的衡量指标分别是类别变量的频次(次数)和频率(占比),可用柱状图可视化。
2.1.2 双变量分析
双变量分析可以发现变量之间的关系,根据其类型的不同可以分为:连续型与连续型、类别型与类别型、类别型与连续型三种双变量分析组合。
1:连续型与连续型:绘制散点图和计算相关性
(a):绘制散点图可以反应变量之间的关系是线性还是非线性
(b):计算相关性可以对变量之间的关系进行量化分析
散点图:

相关性系数公式:
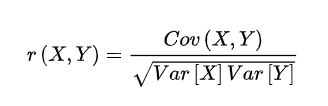
Cov(X,Y)为X与Y的协方差,Var[X]为X的方差,Var[Y]为Y的方差,相关性系数r(X,Y)的取值区间为[-1,1],当相关系数为-1时,表示强负线性相关,当相关性系数为1时,表示强正线性相关,当为0时,表示不相关。
import numpy as np
a=np.array([2,2,8,13,18])
b=np.array([1,2,4,6,10])
print(np.corrcoef(a,b))
=》[[1. 0.98228294]
[0.98228294 1. ]]
一般来说,在取绝对值后,0-0.09为没有相关性,0.1-0.3为弱相关性,0.3-0.5为中等相关,0.5-1.0为强相关,由上r(a,b)=0.98228294可知:a,b强相关
2:类别型与类别型:对于该类型数据一般采用双向表、堆叠柱状图和卡方验证进行分析
(a)双向表:通过建立频次和频率的双向表来分析变量之间的关系,其中行和列分别表示一个变量。
(b)堆叠柱状图:相对比较直观
(c)卡方验证:主要用于两个和两个以上样本率(构成比)及两个二值型离散变量的关联性分析,即比较理论频次和实际频次的吻合程度和拟合优度。
from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
iris=load_iris()
X,Y=iris.data,iris.target
chiValues=chi2(X,Y)
x_new=SelectKBest(chi2,k=2).fit_transform(X,Y)
3:类别型与连续型:在分析类别型和连续型双变量时,可以绘制小提琴图,这样可以分析类别变量在不同类别时另一个连续变量的分布情况,

