吴恩达机器学习课后作业——异常检测和推荐系统(协同过滤算法)
Anomaly detection(异常检测)
一、作业内容
在本练习中,我们将使用高斯模型实现异常检测算法,并将其应用于检测网络上的故障服务器。
在这个练习中,您将实现一个异常检测算法来检测服务器计算机中的异常行为。这些特性测量每个服务器的响应的吞吐量(mb/s)和延迟(ms)。当服务器运行时,您收集了m = 307个关于它们行为的示例,因此有一个未标记的数据集[z(1),.,(m)]。您怀疑这些示例中的绝大多数都是服务器正常运行的“正常”(非异常)示例,但也可能有一些服务器在此数据集中运行异常的示例。
数据集下载位置(包含吴恩达机器学课后作业全部数据集):data
二、作业分析
1、异常检测(anomaly detection):异常检测就是发现与大部分对象不同的对象,其实就是发现离群点。异常检测有时也称偏差检测。异常对象是相对罕见的。用数据集建立概率模型p(x),如果新的测试数据在这个模型上小于某个阈值,则说它极大可能为异常点。
我们通常的做法是构建一个模型,计算p(x),也就是对x的分布概率建模。我们设定一个阈值ε,当p( x t e s t x_{test} xtest)<ε,则判定为异常。当p( x t e s t x_{test} xtest) >= ε时就判定为合格。
2、常见的异常检测的应用:
(1) 欺诈检测:主要通过检测异常行为来检测是否为盗刷他人信用卡。
(2) 入侵检测:检测入侵计算机系统的行为
(3) 医疗领域:检测人的健康是否异常
3、异常检验算法:
(1) 根据训练集数据,计算特征的平均值和方差。
(2) 构建p(x)正态分布函数。
(3) 对交叉检验集,我们尝试使用不同的:值作为阀值,预测数据是否异常,根据F1值或者查准率与查全率的比例来选择t。
(4) 选出ε后,针对测试集进行预测,计算异常检验系统的F1值。
4、检验步骤:
(1) 求均值和方差。
(2) 计算正态分布密度函数。
密度估计(density estimation)使用联合密度函数作为概率模型。
(3) 求阈值ε。
F1的选择基于查准率(Precision),查全率(recall),在验证集上尝试不同的阈值,选择能最大化F1值的阈值。
Step1:求均值和方差
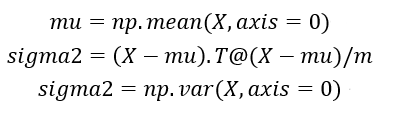
Step2:计算正态分布密度函数p
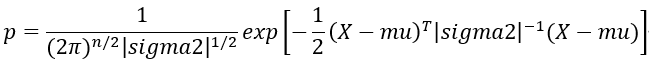
Step3:求阈值ε
TP:预测为1,实际为1,预测正确
FP:预测为1,实际为0,预测错误
TN:预测为0,实际为0,预测正确
FN:预测为0,实际为1,预测错误
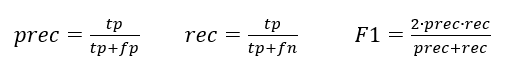
5、高斯分布 (正态分布)
假设x∈实数,且x的均值为u,方差为 σ 2 σ^2 σ2,则用数学符号可以表示为x~N(u, σ 2 σ^2 σ2)
其中u确定了中心位置,σ则确定了山峰的宽度,高斯分布的概率分布函数如下图所示:
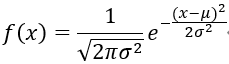
其中:
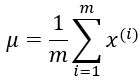
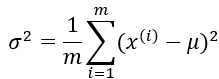
6、多元高斯分布 :特征相关的情况下使用多元高斯分布
(1) 原始模型(一元高斯的乘积):当特征之间存在线性关系时,想通过异常的组合值来捕捉异常样本,必须人工创造新特征捕捉异常。
(2) 计算简单,且较好适应m(训练集数量)小的情况。
(3) 多元高斯模型:自动捕捉特征之间的线性相关(协方差)。
(4) 计算较复杂,必须满足m>n(特征数量),否则协方差矩阵不可逆。且特征间无线性相关。
7、监督学习和异常检测问题的主要区别在以下几个方面:
(1) 在异常检测问题里,大部分都是y=0的样本,很少y=1的样本。而监督学习里会存在大量的y=1的样本。
(2) 因为在异常检测问题里,异常样本很少,所以很难通过有效的学习算法去根据特征判断哪些是异常样本。而在监督学习问题里,我们会有大量的样本去学习特征给正负样本带来的影响。
8、构建多元高斯分布模型:
(1) 准备拟合模型的参数
(2) 引入新的样本,进行异常检测
9、原始模型和多元高斯模型的联系:
(1) 如果多变量高斯模型的协方差矩阵除了对角线之外,全是0。那么多变量高斯模型和原始的模型就是一样的模型。
(2)由于第一点原因,原始的模型的可视化图一定是轴对称的。而多变量高斯模型还可以是y=x对称。因此原始的模型其实是多变量高斯模型的一种特殊情况。
(3)原始的模型,协方差矩阵是对角矩阵,暗示各个特征之间是相互独立的。当使用多变量高斯模型的时候,暗示各个特征之间是有联系的。
10、原始模型和多变量高斯模型的选择:
(1) 原始的模型需要手动建立特征之间的关系,也就是创建新的特征。手动创建的特征,可以使得原始模型运行的更好。
(2) 多变量高斯模型则可以自动捕捉这种不同特征之间的关系。
(3) 原始模型计算成本较低,能够适应更高维的计算。多变量高斯模型要计算逆矩阵,所以计算成本较高。
(4) 对于样本数量m比较小的时候,原始模型也可以计算的很好。但是对于多变量高斯模型,必须使得样本数量m>特征数量n,否则会出现不可逆的情况,比较适合m>=10*n的情况。
注意:
如果在使用多变量高斯模型的时候,发现不可逆了。首先检查m是否大于n,其次检查特征中是否有线性相关的特征,去掉冗余的特征。
三、代码实战
引入所需函数库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat
from scipy import stats
我们的第一个任务是使用高斯模型来检测数据集中未标记的示例是否应被视为异常。
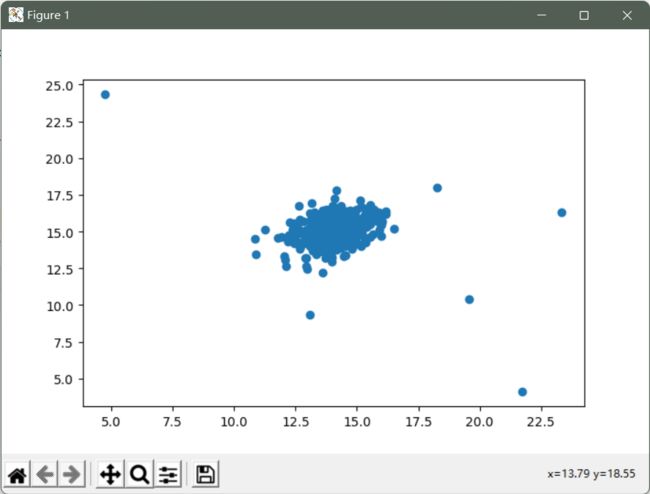
加载数据并且可视化查看数据分布。
# 加载数据
data = loadmat('ex8data1.mat')
X = data['X']
# 绘制散点图查看数据分布
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(X[:,0], X[:,1])
plt.show()
我们正在为数据中的每个特征估计高斯分布。
创建一个返回每个要素的均值和方差的函数。
def estimate_gussian(X):
mu = X.mean(axis=0)
sigma = X.var(axis=0)
return mu, sigma
使用一组标记的验证数据(其中真实异常样本已被标记),并在给出不同阈值的情况下,对模型的性能进行鉴定。
Xval = data['Xval']
yval = data['yval']
计算数据点属于正态分布的概率。
dist = stats.norm(mu[0], sigma[0])
将数组传递给概率密度函数,并获得数据集中每个点的概率密度。
dist.pdf(X[:,0])[0:50]
计算并保存给定上述的高斯模型参数的数据集中每个值的概率密度。
p = np.zeros((X.shape[0], X.shape[1]))
p[:,0] = stats.norm(mu[0], sigma[0]).pdf(X[:,0])
p[:,1] = stats.norm(mu[1], sigma[1]).pdf(X[:,1])
为验证集(使用相同的模型参数)执行此操作。
我们将使用与真实标签组合的这些概率来确定将数据点分配为异常的最佳概率阈值。
pval = np.zeros((Xval.shape[0], Xval.shape[1]))
pval[:,0] = stats.norm(mu[0], sigma[0]).pdf(Xval[:,0])
pval[:,1] = stats.norm(mu[1], sigma[1]).pdf(Xval[:,1])
创建一个函数找到给定概率密度值和真实标签的最佳阈值
我们将为不同的epsilon值计算F1分数。 F1是真阳性,假阳性和假阴性的数量的函数。
def select_threshold(pval, yval):
best_epsilon = 0
best_f1 = 0
f1 = 0
step = (pval.max() - pval.min()) / 1000
for epsilon in np.arange(pval.min(), pval.max(), step):
preds = pval < epsilon
tp = np.sum(np.logical_and(preds == 1, yval == 1)).astype(float)
fp = np.sum(np.logical_and(preds == 1, yval == 0)).astype(float)
fn = np.sum(np.logical_and(preds == 0, yval == 1)).astype(float)
precision = tp / (tp + fp)
recall = tp / (tp + fn)
f1 = (2 * precision * recall) / (precision + recall)
if f1 > best_f1:
best_f1 = f1
best_epsilon = epsilon
return best_epsilon, best_f1
将阈值应用于数据集,并可视化结果
epsilon, f1 = select_threshold(pval, yval)
# 被视为异常值的值的索引
outliers = np.where(p < epsilon)
# 绘图
fig, ax = plt.subplots(figsize=(12,8))
ax.scatter(X[:,0], X[:,1])
ax.scatter(X[outliers[0],0], X[outliers[0],1], s=50, color='r', marker='o')
plt.show()

红点是被标记为异常值的点。 这些看起来很合理。 有一些分离(但没有被标记)的右上角也可能是一个异常值,但是相当接近。
推荐系统(协同过滤算法)
一、作业内容
在本练习中,我们将实现一种称为协作过滤的特定推荐系统算法,并将其应用于 电影评分的数据集。
实现协同过滤算法并将它运用在电影评分的数据集上,最后根据新用户的评分来给新用户推荐10部电影
二、作业分析
1、线性回归的代价函数和梯度
代价函数(正则项):

梯度(正则项):
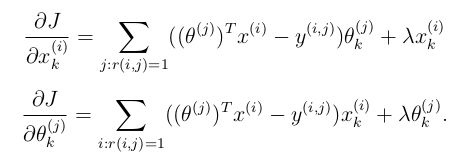
2、协同过滤
根据电影的特征来预测用户参数,再根据得到的用户参数来预测电影特征,循环这个过程

协同过滤算法的流程
(1) 随机初始化参数θ和x
(2) 使用梯度下降优化代价函数,求得最优的θ和x。因为x∈ R n R^n Rn,θ∈ R n R^n Rn,所以正则项不用单独考虑
(3) 给一个用户的θ,可以通过学习到的x,计算θTx来得到用户对于电影的评分。![]()
3、矢量化:低秩矩阵分解
假设我们已经通过协同过滤算法得到了电影的特征x。 x ( i ) x^{(i)} x(i)∈ R n R^n Rn
我们可以通过计算两个电影的特征x之间的距离来找到相似的电影。|| x ( i ) x^{(i)} x(i)- x ( j ) x^{(j)} x(j)||
4、实施细节:均值规范化
Y−μ,可以避免出现因为某用户对所有电影没有评分,而导致该用户所有预测的评分都为零的情况。
预测完之后加回均值μ。相当于预测出的没有评分的用户的评分,为所有用户评分的均值。
三、代码实战
推荐引擎使用基于项目和用户的相似性度量来检查用户的历史偏好,以便为用户可能感兴趣的新“事物”提供建议。在本练习中,我们将实现一种称为协作过滤的特定推荐系统算法,并将其应用于 电影评分的数据集。
引入所需函数库
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sb
from scipy.io import loadmat
from scipy.optimize import minimize
我们首先加载并检查我们将要使用的数据。
data = loadmat('ex8_movies.mat')
print(data)
{'__header__': b'MATLAB 5.0 MAT-file, Platform: GLNXA64, Created on: Thu Dec 1 17:19:26 2011', '__version__': '1.0', '__globals__': [], 'Y': array([[5, 4, 0, ..., 5, 0, 0],
[3, 0, 0, ..., 0, 0, 5],
[4, 0, 0, ..., 0, 0, 0],
...,
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0]], dtype=uint8), 'R': array([[1, 1, 0, ..., 1, 0, 0],
[1, 0, 0, ..., 0, 0, 1],
[1, 0, 0, ..., 0, 0, 0],
...,
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0],
[0, 0, 0, ..., 0, 0, 0]], dtype=uint8)}
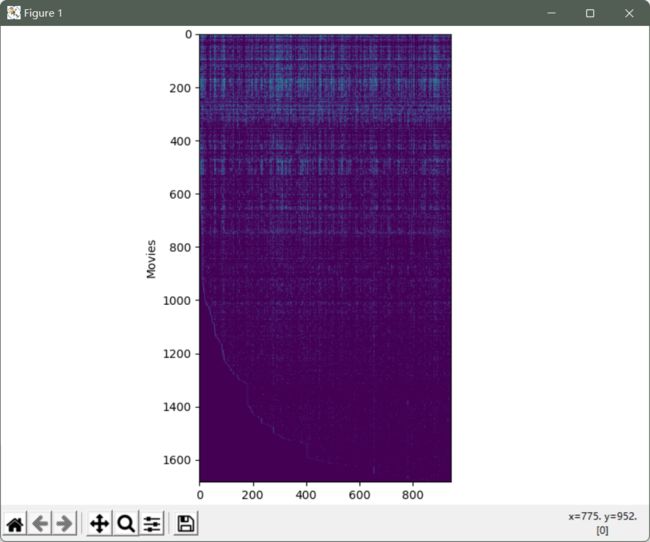
Y是包含从1到5的等级的(数量的电影x数量的用户)数组.R是包含指示用户是否给电影评分的二进制值的“指示符”数组。
将矩阵渲染成图像来“可视化”数据
Y = data['Y']
R = data['R']
# 通过平均排序Y来评估电影的平均评级
Y[1,np.where(R[1,:]==1)[0]].mean()
# 将矩阵渲染成图像
fig, ax = plt.subplots(figsize=(12,12))
ax.imshow(Y)
ax.set_xlabel('Users')
ax.set_ylabel('Movies')
fig.tight_layout()
plt.show()
接下来,我们将实施协同过滤的代价函数。 直觉上,“代价”是指一组电影评级预测偏离真实预测的程度。
它基于文本中称为X和Theta的两组参数矩阵。 这些“展开”到“参数”输入中,以便稍后可以使用SciPy的优化包。
创建协同过滤的代价函数
def cost(params, Y, R, num_features):
Y = np.matrix(Y) # (1682, 943)
R = np.matrix(R) # (1682, 943)
num_movies = Y.shape[0]
num_users = Y.shape[1]
# 将参数数组重塑为参数矩阵
X = np.matrix(np.reshape(params[:num_movies * num_features], (num_movies, num_features))) # (1682, 10)
Theta = np.matrix(np.reshape(params[num_movies * num_features:], (num_users, num_features))) # (943, 10)
# 初始化
J = 0
# 计算代价函数
error = np.multiply((X * Theta.T) - Y, R) # (1682, 943)
squared_error = np.power(error, 2) # (1682, 943)
J = (1. / 2) * np.sum(squared_error)
return J
为了实现梯度计算,我们将扩展代价函数来计算梯度,并在代价和梯度计算中添加正则化
def cost(params, Y, R, num_features, learningRate):
Y = np.matrix(Y) # (1682, 943)
R = np.matrix(R) # (1682, 943)
num_movies = Y.shape[0]
num_users = Y.shape[1]
# 将参数数组重塑为参数矩阵
X = np.matrix(np.reshape(params[:num_movies * num_features], (num_movies, num_features))) # (1682, 10)
Theta = np.matrix(np.reshape(params[num_movies * num_features:], (num_users, num_features))) # (943, 10)
# 初始化
J = 0
X_grad = np.zeros(X.shape) #(1682, 10)
Theta_grad = np.zeros(Theta.shape) #(943, 10)
# 计算代价函数
error = np.multiply((X * Theta.T) - Y, R) # (1682, 943)
squared_error = np.power(error, 2) # (1682, 943)
J = (1. / 2) * np.sum(squared_error)
# 正则化代价函数
J = J + ((learningRate / 2) * np.sum(np.power(Theta, 2)))
J = J + ((learningRate / 2) * np.sum(np.power(X, 2)))
# 使用正则化计算梯度函数
X_grad = (error * Theta) + (learningRate * X)
Theta_grad = (error.T * X) + (learningRate * Theta)
# 将梯度矩阵分解为单个阵列
grad = np.concatenate((np.ravel(X_grad), np.ravel(Theta_grad)))
return J, grad
创建自己的电影评分,以便我们可以使用该模型来生成个性化的推荐。
数据集中我们提供一个连接电影索引到其标题的文件。 接着我们将文件加载到字典中。
# 加载文件并创建自己的电影评分
movie_idx = {}
f = open('data/movie_ids.txt',encoding= 'gbk')
for line in f:
tokens = line.split(' ')
tokens[-1] = tokens[-1][:-1]
movie_idx[int(tokens[0]) - 1] = ' '.join(tokens[1:])
我们将使用练习中提供的评分
# 使用练习中提供的评分
ratings = np.zeros((1682, 1))
ratings[0] = 4
ratings[6] = 3
ratings[11] = 5
ratings[53] = 4
ratings[63] = 5
ratings[65] = 3
ratings[68] = 5
ratings[97] = 2
ratings[182] = 4
ratings[225] = 5
ratings[354] = 5
将评级向量添加到现有数据集中以包含在模型中
R = data['R']
Y = data['Y']
Y = np.append(Y, ratings, axis=1)
R = np.append(R, ratings != 0, axis=1)
定义变量并对评级进行规一化
movies = Y.shape[0] # 1682
users = Y.shape[1] # 944
features = 10
learning_rate = 10.
X = np.random.random(size=(movies, features))
Theta = np.random.random(size=(users, features))
params = np.concatenate((np.ravel(X), np.ravel(Theta)))
for i in range(movies):
idx = np.where(R[i,:] == 1)[0]
Ymean[i] = Y[i,idx].mean()
Ynorm[i,idx] = Y[i,idx] - Ymean[i]
# 进行梯度下降
fmin = minimize(fun=cost, x0=params, args=(Ynorm, R, features, learning_rate), method='CG', jac=True, options={'maxiter': 100})
# 进行解序列化
X = np.matrix(np.reshape(fmin.x[:movies * features], (movies, features)))
Theta = np.matrix(np.reshape(fmin.x[movies * features:], (users, features)))
使用训练好的参数X和Theta,为的用户创建一些建议
predictions = X * Theta.T
my_preds = predictions[:, -1] + Ymean
使用argsort函数来预测评分对应的电影
idx = np.argsort(my_preds, axis=0)[::-1]
print("Top 10 movie predictions:")
for i in range(10):
j = int(idx[i])
print('Predicted rating of {0} for movie {1}.'.format(str(float(my_preds[j])), movie_idx[j]))
结果:
Top 10 movie predictions:
Predicted rating of 5.000083902317881 for movie Star Kid (1997).
Predicted rating of 5.000066301540124 for movie They Made Me a Criminal (1939).
Predicted rating of 5.000063113009334 for movie Entertaining Angels: The Dorothy Day Story (1996).
Predicted rating of 5.000051454276145 for movie Marlene Dietrich: Shadow and Light (1996) .
Predicted rating of 5.000051067514195 for movie Great Day in Harlem, A (1994).
Predicted rating of 5.0000446697609275 for movie Prefontaine (1997).
Predicted rating of 5.000023717974671 for movie Someone Else's America (1995).
Predicted rating of 5.000014156199182 for movie Saint of Fort Washington, The (1993).
Predicted rating of 5.000009635652606 for movie Aiqing wansui (1994).
Predicted rating of 4.999989470189383 for movie Santa with Muscles (1996).
参考链接:https://github.com/fengdu78/Coursera-ML-AndrewNg-Notes
https://blog.csdn.net/weixin_41799019/article/details/118636230?spm=1001.2014.3001.5502