深度学习的Attention机制，看这一篇文章就够了

Attention 机制的由来与发展

看 NLP 方向的论文，几乎每篇都能看到 self-attention、transformer、bert 的出现，如果直接去学习这几个模型的话，很容易迷失在各种矩阵操作中，心里会一直有个疑问，为什么要这么做？但是了解 attention 机制的源头及发展后，心里就慢慢清晰了起来。所以，写这篇文章打算从头梳理一下 attention。

机器翻译理论部分

在 NLP 中给定一个序列，输出另一个序列的任务，称为 seq2seq，也就是序列到序列的任务。也是机器翻译最常用的模型，解决的最大的问题就是输入序列和输出序列的长度不一致问题。

在机器翻译问题中，假设我们有一系列的训练样本 $(x_i,y_i),i=1...n$，其中 $x$ 代表待翻译的句子，$y$ 代表翻译后的句子。
对于每一个训练样本 $(x_i,y_i)$ ，$x,y$ 分别代表两个序列，$x=\left(x^{<1>},x^{<2>},\dots ,x^{<T_x>}\right)$，$y=\left(y^{<1>},y^{<2>},\dots ,y^{<T_y>}\right)$。
例如在中英翻译中，$x=(我，是，中国，人)$ ，$y=(I,am,chinese)$。
根据极大似然估计， 我们的目标函数可以写为最大化:$$P(Y\mid X)=\prod _{i=1}^{n}P\left(Y_i\mid X_i\right)$$
转换成 $\log$ 形式则是最小化:
$$\underset{\theta }{\min }-\frac{1}{N}\sum _{i=1}^N{\log }_{}P\left(Y_i\mid X_i\right)$$
其中$\theta$为模型参数。
现在我们只需要知道$P(Y\mid X)$ 怎么求即可。
首先我们知道：$$P(Y\mid X)=P\left(y^{<1>},y^{<2>},y^{<3>},\dots y^{<T_y>}\mid x^{<1>},x^{<2>},\dots x^{<T_x>}\right)$$
上面这个式子可以用下面的公式转换，由于序列太长，所以只写了一部分举例：
$$P\left(y^{<1>},y^{<2>}\mid x^{<1>},x^{<2>}\right)=P\left(y^{<1>}\mid x^{<1>},x^{<2>}\right)\cdot P\left(y^{<2>}\mid y^{<1>},x^{<1>},x^{<2>}\right)$$
这个式子就是序列模型的原理。下面讲 seq2seq 模型时，就可以对照理解这个式子了。

seq2seq 最初模样

seq2seq 模型被称为条件语言模型（conditional language model）。最早由bengio等人发表在 computer science 上的论文：Learning Phrase Representations using RNN Encoder–Decoder
for Statistical Machine Translation
其结构如下图所示:

Encoder 用 RNN 来构成，每个 time-step 向 Encoder中 输入一个词的向量 $ x^{}$ ，输出为 $h^{<t>}$，直到句子的最后一个单词被输入 $x^{<T_x>}$，得到的输出为句向量 $c=tanh(V{h}^{<T_x>})$。
其中 Encoder 中 RNN 状态更新公式为：
$$h^{<t>}=f\left(h^{<t-1>},x^{<t>}\right),t=1,\dots ,T_x$$
其中 $f$ 代表 RNN，也可以换成 LSTM 或 GRU。
句子向量 $c$ 由 Encoder 最后一刻的输出状态 $h^{<T_x>}$ 变换得到：
$$c=tanh(V{h}^{<T_x>})$$

Decoder 用另一个 RNN 来构成，用来根据之前 Encoder 得到的句向量 $c$ 和前一时刻的结果 $y^{<t-1>}$ 和当前时刻的输出 $h^{<t>}$来得到 $y^{<t>}$，依此类推直到得到结尾输出 EOS。
其中，Decoder 的第一个隐状态 $h^{<0>}$由于没有上一时刻的输出和隐状态输出，$h^{<0>}$的计算公式为:
$$h^{<0>}=\tanh \left(V^{\prime }c\right)$$
其它时刻的$h^{<t>}$计算公式为:
$$h^{<t>}=f\left(h^{<t-1>},y^{<t-1>},c\right),t=1,\dots ,T_x$$
每一时刻的输出 $y^{<t>}$ 计算公式为:
$$P\left(y^{<t>}\mid y^{<t-1>},y^{<t-2>},\dots ,y^{<1>},c\right)=g\left(h^{<t>},y^{<t-1>},c\right)$$
$g$ 函数一般为 softmax。

整个 Decoder 的过程可以理解为：
$$P(y_1,y_2,y_3)=P\left(y_1,c\right)\cdot P\left(y_2\mid y_1,c\right)\cdot P\left(y_3\mid y_1,y_2,c\right)$$

总结：
论文中的给出的这个结构图上显示的相关关系还是非常准确的，每条线都代表着相关关系。
总的来说就是 Encoder 只负责输出一个代表句子的向量 $c$，然后 Decoder 中的每一时刻的 $h^{<t>}$ 计算都与 $c,h^{<t-1>},y^{<t-1>}$ 相关，每一时刻的输出计算都与 $h^{<t>},y^{<t-1>},c$ 相关。

这就延伸出了三个问题：

1. 由于 RNN 长距离梯度消失的问题，句子很长的话，句子向量 $c$ 可能会丢失部分内容的语义信息，并不能很好的代替整个句子的语义。
2. 每次做预测输出或计算，都用到了整个句子的信息 $c$，实际上把 I 翻译 我 并不需要整个句子的信息。
3. 翻译对齐问题，我们在做翻译的时候差不多有个中英对齐的关系，比如 I 翻译成 我，you 翻译成 你。而这个模型里面体现不出来这种对齐关系。

seq2seq的改进模型

改进模型介绍2014年谷歌发表的论文Sequence to Sequence Learning with Neural Networks。
模型如下图:

可以看到，该模型和第一个模型主要的区别在于从输入到输出有一条完整的流：ABC 为 Encoder 的输入，WXYZ 为 Decoder 的输出。将 Encoder 最后得到的隐藏层的状态 ht 输入到 Decoder 的第一个 cell 里，就不用像第一个模型一样，每一个 Decoder 的 cell 都需要 Encoder 中的信息，因此从整体上看，从输入到输出像是一条“线性的数据流”。
同时该论文也提出来，ABC 翻译为 XYZ，输入的时候将 ABC 的变为 CBA 效果更好。论文猜测是因为翻转原句子虽然没有改变 “对应词” 之间的平均距离，但是原句子与目标句子中前几个 “对应词” 之间的距离缩短了，比如 A 和 X 的距离。这样更有利于句子中前几个词的翻译。这从另一方面证明了长序列信息丢失的问题。

“对应词” 在翻译中可以理解为 I 和 我 是一组对应词，you 和 你 是一组对应词。

具体来说，此模型的 Encoder 的过程如下图。这和我们之前的 Encoder 一样。

不同的是 Decoder 的阶段：

这个模型流程比较丝滑，容易理解，就不过多解释了。不过这个模型并没有解决我们一开始说的那三个问题，只不过把 seq2seq 的流程给优化了，更容易理解了。
真正解决问题的是下面要介绍的第一代 attention。

seq2seq with attention

为了解决 seq2seq 中前面说的那三个问题，论文NEURAL MACHINE TRANSLATION BY JOINTLY LEARNING TO ALIGN AND TRANSLATE这时就提出了第一代 attention，即对于 Decoder 中每一个 cell，都检测 Encoder 中每个单词对它重要性。
模型改进的结构如下图：

上图中，Encoder 和 Decoder 都发生了变化。

首先说 Encoder，使用了 双向RNN，解决 RNN 单向性的问题。使用 $ \overrightarrow{h_j} $ 代表 RNN 前向的隐层状态,$\overleftarrow{h_j} $ 代表 RNN 的反向隐层状态，$ h_j$ 的最终状态为将两者连接 concat 起来，即 $h_j=\left[h_j;h_j\right]$

下面说说 Decoder，对于 Decoder 中每时间步的输出公式为:
$$p\left(y_i\mid y_1,\dots ,y_{i-1},\mathbf{x}\right)=g\left(y_{i-1},s_i,c_i\right)$$
即对于时间步 $i$ 的输出 $y_i$，由时间步 $i$ 的隐藏状态 $s_i$，由 attention 计算得到的输入内容 $c_i$ 和上一时间步的输出 $y_{i-1}$ 得到。
其中 $s_i$ 是对于时间步 $i$ 的隐藏状态，计算公式为：
$$s_i=f\left(s_{i-1},y_{i-1},c_i\right)$$

只看公式的话，会发现加入 attention 的 seq2seq 与之前的 seq2seq 只有内容 $c$ 不同，之前的 seq2seq 的 Decoder 中所有的时间步共用一个 $c$ ，而加入了 attention 的 seq2seq 每一个时间步都有一个 $c_i$，那 $c_i$ 是怎么得来的呢？和输入内容以及 attention 有什么关系呢？我们接着看公式:
$$c_i=\sum _{j=1}^{T_x}{\alpha }_{ij}{h}_j$$
即，对于 Decoder 的时间步 $i$ 的内容向量 $c_i$ ，$c_i$ 等于 Encoder 中隐藏状态序 $\left(h_1,\cdots ,h_{T_x}\right)$ 的加权求和，其中每个 $h_j$ 对应的权重 ${\alpha }_{ij}$ 计算公式如下:
$${\alpha }_{ij}=\frac{\exp \left(e_{ij}\right)}{{\sum }_{k=1}^{T_x}\exp \left(e_{ik}\right)}$$
其中 $e_{ij}=a(s_{i-1},h_j)$，$e_{ij}$ 又称 attention score 或 “相似度“ 或 “影响度” 或 “匹配得分”

这里 $a$ 通常是点积计算。这里计算 $e_{ij}$ 写的是原论文公式，用 $s_{t-1}$ 和 $h_i$ 来算，但斯坦福教材上是画的是 $s_t$ 和 $h_i$ 来算，而且后续论文大多是用的这种方式，即当前步的 attention score 用的当前步的隐藏状态 $s_t$ 和 $h_i$ 去算的。

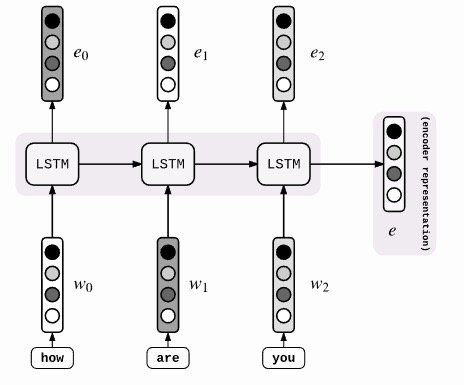
网上找了一个可视化这部分公式计算的图，希望可以帮助大家理解：

最后总结一下该论文：
我们在 Encoder 的过程中得到 双向RNN 单元的隐藏状态序列 $\left(h_1,\cdots ,h_{T_x}\right)$ 。
然后对于 Decoder 中的每一个时间步$i$的隐藏状态 $s_i$，可以通过时间步 $i-1$ 的隐藏状态 $s_{i-1}$、输入内容的编码向量 $c_i$ 和上一个时间步输出 $y_{i-1}$得到。每个时间步的 $c_i$ 都各不相同，$c_i$ 由 attention 机制计算得到，具体步骤见文章。对于每一个时间步 $i$ 的输出 $y_i$，由时间步 $i$ 的隐藏状态 $s_i$，由 attention 计算得到的输入内容 $c_i$ 和上一时间步的输出 $y_{i-1}$ 得到。

attention 通用定义

attention 被提出以来，很快被应用到了各个领域，这里 Stanford 的教授在其教学课件中，给出了一个基本通用的定义：

• 给出一组值向量(values)和一个查询向量(query)，attention是一种根据查询向量(query)计算这组值向量(values)的加权和的方法。

举例： seq2seq 中，哪个是 query，哪个是 values？

• Decoder 中每一个时间步的 $s_t$ 是 query，Encoder 的 hidden states 是 values。

更进一步，这个加权和就是对 values 中的信息的一个有选择性的概要，我们的query 决定了 values 中的哪一部分会被关注，会被着重提取。
同时 attention 也是一种获取一组长度不定的向量(values)依赖于另一个向量(query)的定长表示的方式。

attention 的 q,k,v 定义

在经典论文attention Is All You Need中，给出了 q,k,v 版本的 attention 定义。

An attention function can be described as mapping a query and a set of key-value pairs to an output, where the query, keys, values, and output are all vectors. The output is computed as a weighted sum of the values, where the weight assigned to each value is computed by a compatibility function of the query with the corresponding key.

attention 函数的本质可以被描述为"查询向量（query）"与"键值对(key-value)"这两种不同数据结构的一种运算方式。
举一个非常形象的例子，一听就懂。 attention 的计算过程可以理解为一个和尚去化斋。
现在有一个和尚名字叫 query，要去化斋———化斋可以理解为要饭，饭就是 value。他每天的化斋流程就是，敲开山下每一户人家的门———每一户人家代表一个 key，每一户人家 key 都会根据自家的情况，给和尚 query 不同的饭量 value。比较经典的就是下图，是不是很像和尚敲门化斋。

当然也可以不止有一个和尚，还可以有其它和尚 query2 等等，其它和尚去其它地方化斋，这就是所谓的 multi-head attention。

整个过程可以公式化，流程化成三步如下图：

1. 将 query 和每个 key 进行相似度计算得到权重，常用的相似度函数有点积，拼接，感知机等；
   $$f\left(Q,K_f\right)=\{\begin{array}{ll}{Q}^T{K}_i& \text{ dot product}\\ Q^T{W}_a{K}_i& \text{ general or multiplicative}\\ W_a\left[Q;K_i\right]& \text{ concat }\\ v_a^T\tanh \left(W_{a}Q+U_a{K}_i\right)& \text{ perceptron or addictive}\end{array}$$
2. 一般是使用一个 softmax 函数对这些权重进行归一化；
   $$a_i=\mathrm{soft}\max \left(f\left(Q,K_i\right)\right)=\frac{\exp \left(f\left(Q,K_i\right)\right)}{{\sum }_j\exp \left(f\left(Q,K_j\right)\right)}$$
3. 将权重和相应的键值 value 进行加权求和得到最后的 attention 。目前在 NLP 研究中，key 和 value 常常都是同一个，即 key=value
   $$\text{ attention }(Q,K,V)=\sum _j{a}_i{V}_i$$

attention 的变种

首先从大的概念来讲，针对 attention 的变体主要有两种方式：
1.一种是在 attention 向量的加权求和计算方式上进行创新
2.另一种是在 attention score（匹配度或者叫权值）的计算方式上进行创新
当然还有一种就是把二者都有改变的结合性创新，或者是迁移性创新
attention score 常见的计算方式我们前面已经给出了，所以下面主要介绍向量的加权求和计算方式上进行创新。

self-attention

前面我们介绍了在 seq2seq 模型中的 attention，是 Decoder 中的 query 去和 Encoder 计算 attention score，再后来 NLP 中出来的 attention 多用来在 Encoder 中自己与自己做attention，也就是 self-attention。

比如 Transformer 和 Bert 中，都是在 Encoder 中输入句子或者段落，然后在 Encoder 内完成 attention 的计算。 Encoder 自己与自己算，所以广义上也称为一种 self-attention。

Transformer 中的 slef-attention 李宏毅版本的计算方法如下图:

这里的 q,k,v 都是输入向量 $a$ 通过矩阵变换得到的，不同向量在 Encoder 中与同一时刻输入进来的其它向量做 attention 计算，因为在 Encoder 内部自己与自己计算，所以叫 self-attention。这里主要是强调，self-attention 和 attention 计算理念相同，就是计算对象不同。

追溯原始的话，Self Attention 最早在 2016 年被提出。在文本分类，文本推荐等领域，虽然输入是一个序列（或者说一组向量），但是输出却不是（输出通常为一个值）。我们有 values，但是似乎难以寻找一个额外的 query。例如文本分类中，除了文本本身并没有其他输入。
针对这样的场景，Yang et al.在2016年提出了Self Attention。 顾名思义，self attention 的 query 和 values 都属于同一个序列。

观察到对于一个句子的向量表示，各个词在其中的贡献程度都是不一样的。同样对于一篇文章的向量表示而言，各个句子对其的贡献程度也是不同的。Yang et al. 希望通过 Self attention 机制可以帮助提取出相对更重要的词语或句子。

给出句子层级的 Context 向量 $u_s$，第 $i$ 个句子的 RNN 隐层向量为 $h_i$，求文章的表示向量 $v$，有
$$u_i=\tanh \left(W_s{h}_i+b_s\right)$$
$${\alpha }_i=\frac{\exp \left(u_i^T{u}_s\right)}{{\sum }_i\exp \left(u_i^T{u}_s\right)}$$
$$v=\sum _t{\alpha }_i{h}_i$$

Soft attention、global attention

这两个就是我们上面讲过的那种最常见的 attention，是在求注意力分配概率分布的时候，对于输入句子 X 中所有单词都给出个概率，是个概率分布，换句话说，就是给所有 value 一个权重。如下图：

Hard attention

事实上，attention 输出并不一定要通过 Softmax 和加权和获得。Soft是给每个单词都赋予一个权重(概率)，那么如果不这样做，直接从输入句子里面找到某个特定的单词，然后把目标句子单词和这个单词对齐，而其它输入句子中的单词硬性地认为对齐概率为 0，这就是 Hard Attention Model 的思想。
这种方法虽然快速，其不可导的特性也为模型训练带来了困难，需要引入variance reduction 或者强化学习来帮助学习。

local attention （半软半硬attention）

我们之前介绍的 attention 都是对整组向量进行的 attention 操作，但是当向量数量很多（长句子，图像）时，计算的消耗(Softmax 是一个耗时操作)会很大，这其实也是 Hard Attention 提出的初衷。但是 Hard Attention 不可导的特性也带来了一些困难，有没有既可导又可以减少计算时间的方法呢？ Local Attention 就是这样被提出来的。

相对于 global attention (对整组向量进行 attention 计算), local attention 只对一个窗口内的向量进行 attention 计算。先根据 Decoder 当前时步选择一个 Encoder 对应的位置 $p_t$ 作为基准位置，然后取 $[p_t-D,p_t+D]$ 作为计算窗口，这里的 $D$ 是根据经验取的超参数。之后对窗口内向量计算 attention 输出。

这里对于 $p_t$ 的取法论文给出了两种变体，一种是简单的一一对应。即 $p_t=t$，Decoder 的第一时步即对应 Encoder 的第一个输入位置，第二时步则对应 Encoder 的第二个输入位置，依次类推。此时的 attention 计算也和 global attention 一致，唯一的不同是只对窗口内元素进行计算。

第二种方法是 joint learning 一个预测网络层来预测 $p_t$ 的值。论文中给出的方法是 $$p_t=S\cdot \mathrm{sigmoid}\left(v_p^T\tanh \left(W_p{h}_t\right)\right)$$
这里 $W_p$ 和 $v_p$ 是可学习的模型参数，$S$ 是输入句子的长度，$h_t$ 是 Decoder 在 $t$ 时刻的隐层向量。此时 attention的计算在 softmax 的基础上乘上了一个高斯分布项使得靠近 $p_t$ 的输入能有更高的权重。
$${\alpha }_t(s)=\mathrm{arign}\left(h_t,h_s\right)\exp \left(-\frac{{\left(s-p_t\right)}^2}{2{\sigma }^2}\right)$$
这里 $s$ 是一个位于 $[p_t-D,p_t+D]$ 的整数，表示对应第 $s$ 个 Encoder输入。相应的是 Encoder 第 $s$ 个输入相对于 Decoder 第 $t$ 个输出的 attention 权重，$h_s$ 是第 $s$ 个 Encoder 输入的隐层向量，$h_t$ 是 Decoder 在 $t$ 时刻的隐层向量，$align()$ 是 global attention 中计算 attention 权重的方式，$\sigma =\frac{D}{2}$。

Scaled Dot-Prodcut Attention

这里主要讲 Transformer 模型的 attention 设计。 Transformer 同样采用了 Key-Value Attention 的设计，不过出于性能考虑，它使用的不是 addictive 的形式，而是 dot product 形式:
$$\mathrm{Attention}(Q,K,V)=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

其中
$$Q\in {\mathbf{R}}^{|Q|\times d_k}，K\in {\mathbf{R}}^{|K|\times d_k},V\in {\mathbf{R}}^{|K|\times d_v}$$

$Q$ 是 query 向量构成的矩阵，|Q|是 query 的数量。$K$ 是 Key 向量构成的矩阵，|K| 是 key 的数量，同时也是 key-value 对中的 value 的数量。 $V$ 是 values 向量构成的矩阵。分母 $\sqrt{d_k}$ 是一个数值上的处理，为避免 dot product 过大而引入的缩放项, $d_k$ 是 key 向量维度，也是 query 向量的维度。
也可以把矩阵形式拆开，写为
$$\mathrm{Attention}(q,K,V)=\sum _i\frac{e^{q\cdot k_i}}{{\sum }_j{e}^{q\cdot k_j}}{v}_i$$
注意 $q$ 和 $k$ 的维度都是 $d_k$, 而 $v$ 的维度是 $d_v$ 。

这里要注意一点，虽然 Transformer 也是采用的 Self Attention，但是这里的 Self Attention 不同于我们在之前的 [Yang, Zichao, et al 2016] 中看到的 Self Attention。之前我们看到的 Self Attention 可以理解为把每一个 query 都作为一个同参数向量来 joint learning 的，而这里采用的 query 向量就是这个词语的词向量（在后面提到的 Multi-head 版本中是词向量的降维形式）。他们的 keys 和 values 都是一致的，均为句子中各个词语的词向量。

这里李宏毅版本的 Transformer 见self-attention那一节，里面的 q,k,v 并不是直接用的词向量，和这里说法不一致，我觉得没有谁对谁错，两种应该都可以。

Multi-Head Attention

单层的 attention 涵盖的信息可能不足以支持多种下游任务, Transformer 在前面 attention 的设计之上继续叠加成为了 Multi-Head Attention。

$$\mathrm{MultiHead}(Q,K,V)=\mathrm{Concat}(hea{d}_1,\dots ,head{}_h)W^O$$
其中$$hea{d}_i=\mathrm{Attention}\left(Q{W}_i^Q,K{W}_i^K,V{W}_i^V\right)$$
这里 $W_i^Q\in {\mathbf{R}}^{d_{\text{model }}\times d_k},W_i^K\in {\mathbf{R}}^{d_{\text{model }}\times d_k},W_i^V\in {\mathbf{R}}^{d_{\text{model }}\times d_v},W^O\in {\mathbf{R}}^{h{d}_v\times d_{\text{model }}}$. 其中 $d_{\text{model }}$ 是模型中q, $\mathrm{k}$, v向量的维度, 在 Transformer 模型中输入的单条 query, key, value 向量的维度都是一样的, 这里用 $d_{\text{model }}$ 表示。
$h$ 是 Multi-Head 的 Head 数, 即并行输出的 Attention 层的层数, 是一个超参数, 在模型中取 8。
$d_k,d_v$ 是将高维的 $d_{\text{model }}$ 维度通过相应的 $W$ 矩阵映射后的维度, 在模型中取 $d_k=d_v=d_{\text{model }}/h=64$ 。这里对原向量进行降维，只是一种架构选择。

下面我们结合上式对计算 MultiHead Attention 的过程进行一个描述。

我们首先对输入的高维向量 $Q,K,V$ 通过 $W$ 矩阵进行降维, 然后进行 Scaled Dot-Product Attention 得到我们的 Attention 输出, 再将输出拼接在一起, 通过 $W^O$ 矩阵还原为高维形式。
通过引入 Multi-Head 和相应的降维操作, 我们的计算量实际上和单一层数近似, 同时又获得了更丰富的表征。

总结

attention 机制从解决 Seq2Seq 中信息瓶颈问题而来，用加权和的形式聚合向量，简单而有效。只要我们使用了加权求和，不管你是怎么花式加权，花式求和，只要你是根据了已有信息计算的隐藏状态的加权和求和，那么就是使用了 attention，而所谓的 self-attention 就是仅仅在句子内部做加权求和。而 key-value 其实是对 attention 进行了一个更广泛的定义罢了，我们前面的 attention 都可以套上 q,k,v 的定义，只不过我们很多时候 k = v，做 self-attention 的时候存在 q = k = v 的时候。

当我们在模型中具体运用它时，陶陶君子总结了以下几点可以提供一个设计和思考的方向：

1. 确定场景中的 query 和 values（或者query, key-values）
2. 确定 attention score 计算方法
3. 根据问题考虑是否采用更特殊的 attention 设计
4. 优化 attention 性能

下面针对这几点进行一个更详细的说明。

• 确定场景中的 query 和 values。 例如在 Seq2Seq 中，query 是 Decoder中当前待翻译的词语，values 是 Encoder 中的各个词语的隐向量。在 Self-Attention 中，query 可以用一个待学习的向量代替，也可以用当前词向量（或其映射）做 query ，values 则是整个句子的各个词向量。在 VQA 中，问题文本的一个词是 query，图像的 feature map 是 values，同时图像的一个区域是 query，问题文本的各个词语是 values。其他领域的 query 和 values，以及 query, key-values 也可以类似的确定。

• 确定 Attention Score计算方法。最常用的点乘(Dot product)和加法(Additive)，以及其他各个变种(如乘法(Multiplicative)，拼接(Concat))。可以从query 和 values(keys) 的维度，计算效率，训练难度，还有问题本身的结构和性质等方面考虑。如果 query 和 values(keys) 维度一样，那么可以直接点乘，不一样的话需要考虑用乘法形式，不一样时也可以用拼接或者加法形式。点乘的计算效率比加法高，但是也要注意数值上的突变问题，考虑像 Transformer 一样加入 scala 缓和该问题。如果问题本身有特殊的结构，相似性度量方法，需要根据具体情况选用相应的形式。

• 更特殊的 Attention 设计

  • multi-head 设计。如果有多个下游任务，或者目标任务需要关注的信息较多，那么可以采取多层 attention 设计。是否需要像 Transformer 一样对各层输入进行降维可以根据计算量和模型结构决定。是否需要像 Lin et al.那样在多维模型 [Lin et al. 2017] 中那样加入惩罚项，可以对 attention 权重进行可视化后，判断是否有效的学习到了多种信息后再决定。
  • 层次设计。这个由问题特性决定。例如文章-句子-词语，句子-词语-字等天然具有层次特性。事实上多层次对模型结构本身影响不大，主要是需要避免训练过于困难。
  • Co-Attention 设计。这个也由问题特性决定，问题中如果query和values具有对称性可以考虑。

• 优化Attention性能。 在大规模的应用中，常常会遇到性能瓶颈，这时候可以考虑对 Attention 性能进行进一步的优化。

  • 确定 attention的范围 local attention 还是 global attention，是固定窗口还是通过学习参数矩阵来预测，窗口的方向是双向还是单向。
  • Hard Attention。 Hard Attention带来了一些训练和设计的困难，但是也减少了计算量。
  • 因子分解。可以考虑分解成多个因子，保留最关键的计算部分，如在特定 cv 领域可以删掉计算 query 和 values 内容相关性的部分。

参考链接：
自然语言处理中的Attention机制总结 - csdn
Attention机制的前世今生 - 知乎
seq2seq 与attention机制 - 网易云课堂(免费课程)
Sequence to Sequence模型 - 知乎
深度学习中注意力机制(attention)的真实由来 - b站
seq2seq模型详解 - csdn
从自然语言处理说说Attention机制 - 知乎
台大李宏毅21年机器学习课程 self-attention和transformer - b站