pytorch 实现MNIST手写数字识别

在之前的文章中，我们使用pytorch下载并转换了MNIST的数据集，今天我们实现LeNet-5网络，使用下载的训练集对网络进行训练，然后使用测试集测试最终的效果。
MNIST数据集详解及可视化处理（pytorch）
首先，我们先看一下LeNet-5，LeNet-5是由“深度学习三巨头”之一、图灵奖得主Yann LeCun在一篇名为"Gradient-Based Learning Applied to Document Recognition"的paper（paper下载地址：https://www.researchgate.net/publication/2985446_Gradient-\Based_Learning_Applied_to_Document_Recognition ）中提出的神经网络结构，在手写数字和机器打印字符上十分高效。

LeNet-5共有7层，不包含输入，每层都包含可训练参数；每个层有多个Feature Map，每个FeatureMap通过一种卷积滤波器提取输入的一种特征。
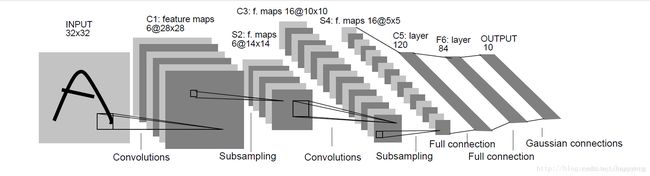它是一个简单的前馈神经网络，它接受一个输入，然后一层接着一层地传递，最后输出计算的结果。

我们可以对LeNet-5的每一层分别做一个分析：

1.首先输入图像是单通道的3232大小的图像，用矩阵表示就是[1,32,32]。
2. c1卷积层，conv1所用的卷积核尺寸为55，滑动步长为1，卷积核数目为6，那么经过该层后图像尺寸变为28，32-5+1=28，输出矩阵为[6,28,28]。
3. s2池化层，pool核尺寸为22，步长2，这是没有重叠的max pooling，池化操作后，图像尺寸减半，变为14×14，输出矩阵为[6,14,14]。
4. c3卷积层，conv2的卷积核尺寸为55，步长1，卷积核数目为16，卷积后图像尺寸变为10,这是因为14-5+1=10，输出矩阵为[16,10,10]。
5. s4池化层，pool核尺寸为22，步长2，这是没有重叠的max pooling，池化操作后，图像尺寸减半，变为5×5，输出矩阵为[16,5,5]。
6. c5卷积层，使用55的卷积核对s4的输出进行卷积，卷积核数目为120，输出图片大小为5-5+1=1，最终输出120个11的特征图。这里实际上是与S4全连接了，但仍将其标为卷积层，原因是如果LeNet-5的输入图片尺寸变大，其他保持不变，那该层特征图的维数也会大于11。
7. F6全连接层，与C5层全连接，神经元个数为84。
8. output输出层，与F6层全连接，输出长度为10的张量，代表所输入的图像属于哪个类别。

现在我们在pytorch框架上实现LeNet-5网络，由于MNIST数据集的图像为28x28单通道，所以我们对LeNet-5网络结构进行了轻微的调整。下面是对修改后的完整代码，请参考。

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
torch.__version__


BATCH_SIZE=512 #大概需要2G的显存
EPOCHS=20 # 总共训练批次
DEVICE = torch.device("cuda" if torch.cuda.is_available() else "cpu") # 让torch判断是否使用GPU，建议使用GPU环境，因为会快很多


#下载训练集
train_loader = torch.utils.data.DataLoader(
        datasets.MNIST('data', train=True, download=True, 
                       transform=transforms.Compose([
                           transforms.ToTensor(),
                           transforms.Normalize((0.1307,), (0.3081,))
                       ])),
        batch_size=BATCH_SIZE, shuffle=True)

#下载测试集
test_loader = torch.utils.data.DataLoader(
        datasets.MNIST('data', train=False, transform=transforms.Compose([
                           transforms.ToTensor(),
                           transforms.Normalize((0.1307,), (0.3081,))
                       ])),
        batch_size=BATCH_SIZE, shuffle=True)

#定义卷积神经网络
class ConvNet(nn.Module):
    def __init__(self):
        super().__init__()
        # batch*1*28*28（每次会送入batch个样本，输入通道数1（黑白图像），图像分辨率是28x28）
        # 下面的卷积层Conv2d的第一个参数指输入通道数，第二个参数指输出通道数，第三个参数指卷积核的大小
        self.conv1 = nn.Conv2d(1, 10, 5) # 输入通道数1，输出通道数10，核的大小5
        self.conv2 = nn.Conv2d(10, 20, 3) # 输入通道数10，输出通道数20，核的大小3
        # 下面的全连接层Linear的第一个参数指输入通道数，第二个参数指输出通道数
        self.fc1 = nn.Linear(20*10*10, 500) # 输入通道数是2000，输出通道数是500
        self.fc2 = nn.Linear(500, 10) # 输入通道数是500，输出通道数是10，即10分类
    def forward(self,x):
        in_size = x.size(0) # 在本例中in_size=512，也就是BATCH_SIZE的值。输入的x可以看成是512*1*28*28的张量。
        out = self.conv1(x) # batch*1*28*28 -> batch*10*24*24（28x28的图像经过一次核为5x5的卷积，输出变为24x24）
        out = F.relu(out) # batch*10*24*24（激活函数ReLU不改变形状））
        out = F.max_pool2d(out, 2, 2) # batch*10*24*24 -> batch*10*12*12（2*2的池化层会减半）
        out = self.conv2(out) # batch*10*12*12 -> batch*20*10*10（再卷积一次，核的大小是3）
        out = F.relu(out) # batch*20*10*10
        out = out.view(in_size, -1) # batch*20*10*10 -> batch*2000（out的第二维是-1，说明是自动推算，本例中第二维是20*10*10）
        out = self.fc1(out) # batch*2000 -> batch*500
        out = F.relu(out) # batch*500
        out = self.fc2(out) # batch*500 -> batch*10
        out = F.log_softmax(out, dim=1) # 计算log(softmax(x))
        return out



#训练
def train(model, device, train_loader, optimizer, epoch):
    model.train()
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = data.to(device), target.to(device)
        optimizer.zero_grad()
        output = model(data)
        loss = F.nll_loss(output, target)
        loss.backward()
        optimizer.step()
        if(batch_idx+1)%30 == 0: 
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                100. * batch_idx / len(train_loader), loss.item()))

#测试
def test(model, device, test_loader):
    model.eval()
    test_loss = 0
    correct = 0
    with torch.no_grad():
        for data, target in test_loader:
            data, target = data.to(device), target.to(device)
            output = model(data)
            test_loss += F.nll_loss(output, target, reduction='sum').item() # 将一批的损失相加
            pred = output.max(1, keepdim=True)[1] # 找到概率最大的下标
            correct += pred.eq(target.view_as(pred)).sum().item()

    test_loss /= len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))


if __name__ == '__main__':
    model = ConvNet().to(DEVICE)
    optimizer = optim.Adam(model.parameters())

    for epoch in range(1, EPOCHS + 1):
        train(model, DEVICE, train_loader, optimizer, epoch)
        test(model, DEVICE, test_loader)

    
    #保存训练完成后的模型
    torch.save(model, './MNIST.pth')

运行上面的代码，我们可以在终端观察训练的进度和损失函数的变化。最终，训练完成的模型对测试集的识别精度达到了99%。

Train Epoch: 20 [14848/60000 (25%)]     Loss: 0.003373
Train Epoch: 20 [30208/60000 (50%)]     Loss: 0.004190
Train Epoch: 20 [45568/60000 (75%)]     Loss: 0.000780

Test set: Average loss: 0.0433, Accuracy: 9904/10000 (99%)

在模型训练完成后，我们调用 torch.save 保存训练好的模型，以便在进行测试和验证时直接加载使用。

下一期我们就从MNIST数据集可视化处理的图片中随机选取几张，输入到本次训练好的模型中进行测试。