基于BP神经网络的人口预测

一、人工神经网络

1.1 人工神经元

人工神经元是对生物神经元的模拟，这种信号传输由输入信号x、突触权重ω、内部阈值θ_j和输出信号y来模拟，如图：

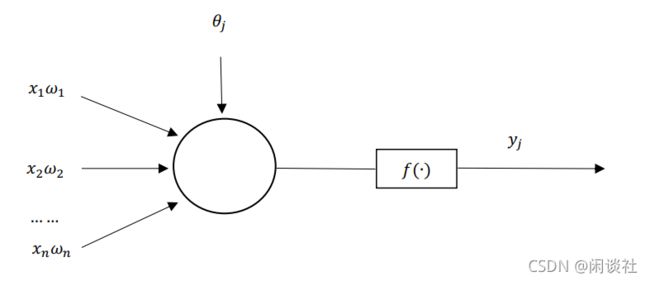
可见，简单神经元的数学表达式为：$y=f({\sum }_{i=1}^n{w}_i.x_i-{\theta }_i)$
1.2 BP人工神经网络（Back Propagation）
BP人工神经网络由输入层、隐含层、输出层三层组成，核心是通过一边向后传递误差，一边修正误差，以此来不断调整网络参数，以实现或逼近所希望输入、输出量之间的映射关系。

二、搭建BP神经网络

2.1 利用MATLAB搭建BP人工神经网络的步骤：

1. 读取数据，并作归一化处理；
2. 划分训练集和测试集；
3. 构建BP神经网络；
4. 网络参数配置；
5. BP神经网络训练；
6. 仿真计算；
7. 计算与测试集之间的误差

2.2 BP人工神经网络人口模型预测

1. 选取1961-2010年人口数据作为训练集，2011-2015年人口数据作为测试集，搭建BP神经网络，并以此预测2016-2020年的人口数据。
2. 隐含层神经元的个数：10，通过经验公式确定： $\sqrt{(}a+b)$，n为输入层层数，m为输出层层数，a∈[0,10] 隐含层
3. 神经元的传输函数：tansig （正切S型传递函数）
4. 输出层的传输函数：purelin（线性传递函数）
5. 反向传播的训练函数：trainlm（Levenberg-Marquardt算法，即非线性最小二乘法）
   

因为BP神经网络训练过程中，是根据每个节点的计算误差不断修正调整连接层的权值ω、阈值θ_j，所以每次计算结果会有偏差。选取拟合结果比较好的两次如下：

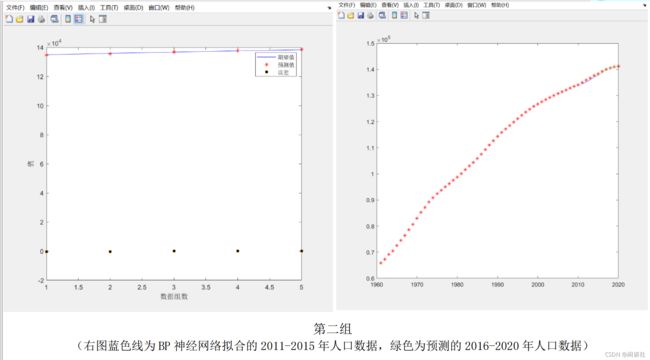
三、数据比较

将BP人工神经算法与改进后的Logistics算法的拟合效果进行对比，拟合误差以均方根误差为比较标准。
模型 2011-2015的拟合误差 2016-2020的预测误差

改进的Logistics算法	306.7126	792.9019
BP神经网络算法（第1组）	106.1849	415.5135
BP神经网络算法（第2组）	277.2575	134.0518

四、MATLAB代码

clear all  
	clc  
	clf  
	
	%% 1，读取1961-2015的人口数据，并做归一化处理  
	input_1=[65859,67296,69172,70499,72538,74542,76368,78534,80671,82992,85229,87177,89211,90859,92420,93717,94974,96259,97542,98705,100072,101654,103008,104357,105851,107507,109300,111026,112704,114333,115823,117171,118517,119850,121121,122389,123626,124761,125786,126743,127627,128453,129227,129988,130756,131448,132129,132802,133450,134091,134916,135922,136726,137646,138326];  
	n=length(input_1);  
	row=4;      %通过前四年数据，预测第五年  
	input=zeros(4,n-row);  
	for i =1:row  
	    input(i,:)=input_1(i:n-row+i-1);  
	end  
	output=input_1(row+1:end);  
	[inputn,inputps]=mapminmax(input);  
	[outputn,outputps]=mapminmax(output);  
	
	%% 2，划分训练集和测试集  
	inputn_train=inputn(:,1:n-row-5);  
	inputn_test=inputn(:,n-row-4:end);  
	outputn_train=outputn(1:n-row-5);  
	outputn_test=outputn(n-row-4:end);  
	
	%% 3，构建BP神经网络  
	hiddennum=10;%隐含层节点数量经验公式p=sqrt(m+n)+a ，故分别取3~13进行试验  
	net=newff(inputn_train,outputn_train,hiddennum,{'tansig','purelin'},'trainlm');     %tansig ：正切S型传递函数。purelin：线性传递函数。trainlm：Levenberg-Marquardt算法   
	
	%% 4，网络参数配置  
	net.trainParam.epochs=1000;  
	net.trainParam.lr=0.2;    
	
	%% 5，BP神经网络训练  
	[net,tr]=train(net,inputn_train,outputn_train);   
	%% 6，仿真计算  
	resultn=sim(net,inputn_test);  
	
	%% 7，计算与测试集之间误差  
	result=mapminmax('reverse',resultn,outputps);  
	output_test=mapminmax('reverse',outputn_test,outputps);  
	error=result-output_test;  
	rmse=sqrt(error*error')/length(error)； 
	figure(1)  
	plot(output_test,'b')  
	hold on  
	plot(result,'r*');  
	hold on  
	plot(error,'s','MarkerFaceColor','k')  
	legend('期望值','预测值','误差')  
	xlabel('数据组数')  
	ylabel('值')  
	
	%% 8，预测未来五年2016-2020的人口数据  
	pn=5;  
	[p_in,ps]=mapminmax(input_1(n-row+1:end));  
	p_in=p_in';  
	p_outn=zeros(1,pn);  
	for i = 1:pn  
	    p_outn(i)=sim(net,p_in);  
	    p_in=[p_in(2:end);p_outn(i)];  
	end  
	p_out=mapminmax('reverse',p_outn,ps)  
	error2=p_out-[139232,140011,140541,141008,141178];  
	rmse2=sqrt(error2*error2')/length(error2)  
	  
	figure(2)  
	plot(1961:2020,[input_1,139232,140011,140541,141008,141178],'r*')  
	hold on  
	plot(2011:2015,result,'b')  
	hold on  
	plot(2015:2020,[result(end),p_out],'g')