gitchat训练营15天共度深度学习入门课程笔记(六)

4.3　数值微分

4.3.1　导数

导数定义公式如下：
$$\frac{df(x)}{dx}=\underset{h\to 0}{\lim }\frac{f(x+h)-f(x)}{h}$$
数值微分方法（用数值方法计算导数）实现：

def numerical_diff(f,x):
	h=10e-50
	return (f(x+h)-f(x))/h

这种方法产生误差原因：

• 这种方式对于特别小的数会出现舍入误差，如float32表示1e-50时，就因为1e-50太小，就直接表示成了0.0。
• h不可能无限小
• 这种方法是数值微分：用数值方法计算导数，而解析性求导得到的是真的导数

所以这里为了进一步减小误差，采取中心差分的方法求导数，而不采用向前差分和向后差分。

def numerical_diff(f,x):
	h=1e-4 #减小舍入误差
	return((f(x+h)-f(x-h))/2*h)

4.3.2　数值微分的例子

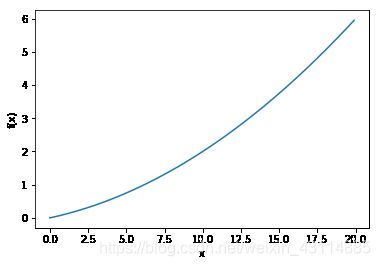
我们下面用python来实现一个函数的导数，函数式如下：
$$y=0.01x^2+0.1x$$

import numpy as np
import matplotlib. pylab as plt
def function_1(x):
    return 0.01*x**2 + 0.1*x
x=np.arange(0.0,20.0,0.1)
y=function_1(x)
plt.xlabel("x")
plt.ylabel("f(x)")
plt.plot(x, y)
plt.show()

绘制出该函数的图像如下：

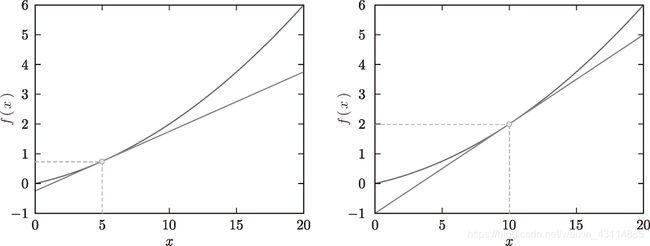
再将带入numerical_diff(f,x)求$x=5$和$x=10$的导数的值

print(numerical_diff(function_1,5))
print(numerical_diff(function_1,10))

运行结果如下：
1.9999999999908982e-09
2.999999999986347e-09

而真的导数为：
$$\frac{df(x)}{dx}=0.02x+0.1$$
在$x=5$和$x=10$处导数的值为0.2和0.3
并且得到的函数切线图像如下，代码在课程的ch04/gradient_1d.py里：

4.3.3　偏导数

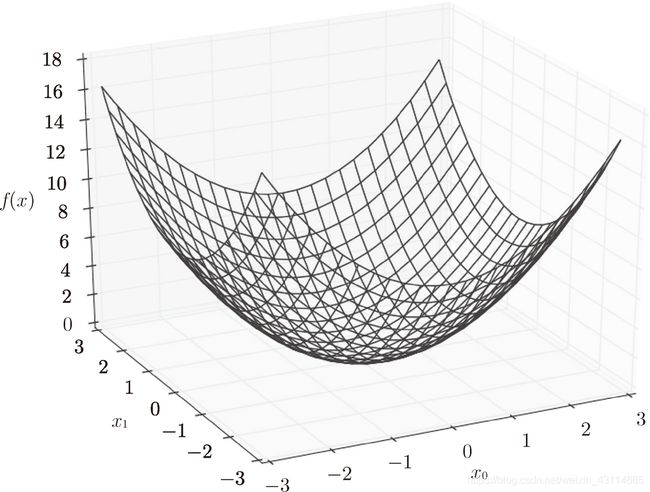
当有两个变量时，表示函数在某处的变化率就需要求偏导了，如函数：
$$f(x_0,x_1)=x_0^2+x_1^2$$
python实现如下：

def function_2(x):
	return np.sum(x**2)

这个函数的图像是三维的：

下面实现求在$x_0=3$和$x_1=4$的情况下的$\frac{\partial y}{\partial x_0}$和$\frac{\partial y}{\partial x_1}$

def function_tmp1(x0):
	return x0*x0+2*4
print(numerical_diff(function_tmp1,3.0))

运行结果如下：
6.000000000003781e-08

def function_tmp1(x1):
	return 2*3+x1*x1
print(numerical_diff(function_tmp1,4.0))

运行结果如下：
7.999999999999119e-08
对于上面的这个例子，简单来说，就是要求哪个变量的偏导，就把另一个变量看作常量就可以了。

4.4　梯度

• 梯度：由全部变量的偏导汇总而成的向量，如($\frac{\partial y}{\partial x_0}$，$\frac{\partial y}{\partial x_1}$)

实现求一个数组的代码如下：

def numerical_gradient(f, x):
    h = 1e-4 # 0.0001
    grad = np.zeros_like(x) # 生成和x形状相同的数组,其中元素全部为0
    for idx in range(x.size): #遍历数组x
        tmp_val = x[idx] #把x的第idx个元素给tmp_val
        # f(x+h)的计算
        x[idx] = tmp_val + h #x[idx]+h放回x数组
        fxh1 = f(x)#把函数的值全计算一遍，x[idx]+h处不同
        # f(x-h)的计算
        x[idx] = tmp_val - h  #x[idx]-h放回x数组
        fxh2 = f(x)#把函数的值全计算一遍，x[idx]-h处不同
        grad[idx] = np.sum((fxh1 - fxh2) / (2*h))#只有idx处的值不同，相减非0，相当于求出了idx处变量的偏导
        x[idx] = tmp_val # 还原值      
    return grad
print(numerical_gradient(function_2, np.array([3.0, 4.0])))
print(numerical_gradient(function_2, np.array([0.0, 2.0])))
print(numerical_gradient(function_2, np.array([3.0, 0.0])))

如果把梯度都花在一幅图上

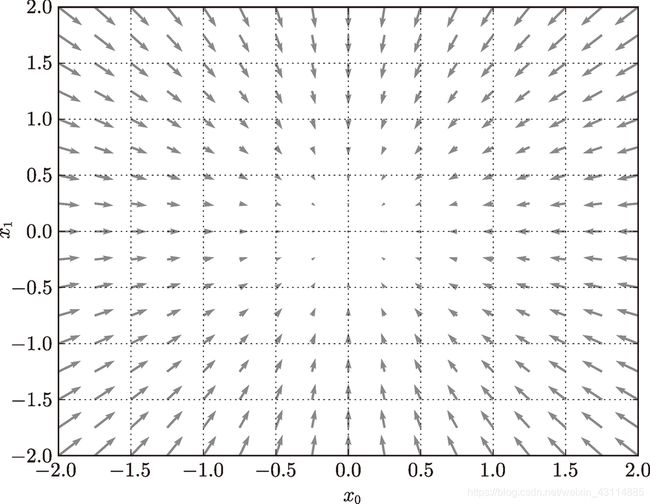
• 梯度指向函数 $f(x_0,x_1)$ 的“最低处”（最小值）
• 离“最低处”越远，箭头越大
• 实际上，梯度会指向各点处的函数值降低的方向。更严格地讲，梯度指示的方向是各点处的函数值减小最多的方向
• 方向导数 = cos(θ) × 梯度，因此，所有的下降方向中，梯度方向下降最多。

方向导数如:$$\frac{\partial y}{\partial l}=\frac{\partial y}{\partial x_0}\cos \alpha +\frac{\partial y}{\partial x_1}\cos \beta$$

4.4.1　梯度法

机器学习和深度学习就是要在学习时找最优参数，而最优参数能使损失函数值最小，所以我们就可以利用梯度。

• 沿着梯度的方向能够最大限度地减小函数的值
• 函数的极小值、最小值以及被称为鞍点（saddle point）的地方，梯度为 0

梯度法：函数的取值从当前位置沿着梯度方向前进一定距离，然后在新的地方重新求梯度，再沿着新梯度方向前进，如此反复，不断地沿梯度方向前进。
梯度法公式：
$$x_0=x_0-\eta \frac{\partial f}{\partial x_0}$$
$$x_1=x_1-\eta \frac{\partial f}{\partial x_1}$$

η 表示更新量，在神经网络的学习中，称为学习率（learning rate）。学习率决定在一次学习中，应该学习多少，以及在多大程度上更新参数，并且要在学习前和学习时不断确定它（人工设定的超参数）。
python实现：

def gradient_descent(f, init_x, lr=0.01, step_num=100): #lr是学习率，step_num是梯度法重复次数
    x = init_x

    for i in range(step_num): 
        grad = numerical_gradient(f, x)
        x -= lr * grad

    return x

使用这个函数可以求函数的极小值，顺利的话，还可以求函数的最小值，如：

def function_2(x): #定义了一个需要两个变量的函数
    return x[0]**2 + x[1]**2

init_x = np.array([-3.0, 4.0])
print(gradient_descent(function_2, init_x=init_x, lr=0.1, step_num=100))

运行结果如下：
[-6.11110793e-10 8.14814391e-10]
非常接近（0，0）

梯度法更新过程，代码在课程的ch04/gradient_method.py里：

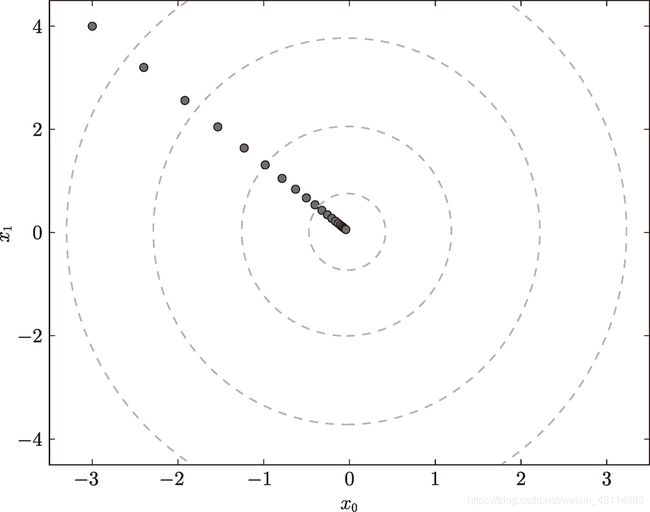
• 学习率过大，每次更新的值会变得很大
• 学习率过小，没怎么更新就结束了

4.4.2　神经网络的梯度

• 损失函数的梯度$\frac{\partial L}{\partial \mathbf{W}}$ 的形状和 权重参数$\mathbf{W}$ 相同

简单神经网络实现梯度：

import sys, os
sys.path.append(os.pardir)
import numpy as np
from common.functions import softmax, cross_entropy_error #引入softmax函数和交叉熵误差函数
from common.gradient import numerical_gradient #引入梯度函数

class simpleNet:
    def __init__(self):
        self.W = np.random.randn(2,3) # 用高斯分布进行权重初始化

	def predict(self, x):
        return np.dot(x, self.W) 

	def loss(self, x, t):
    	z = self.predict(x) #矩阵乘法求加权和到输出层前
		y = softmax(z) #softmax函数输出层激活函数
		loss = cross_entropy_error(y, t) #交叉熵误差函数实现损失函数

		return loss
def f(W):
	return net.loss(x, t)
	
net = simpleNet()
x = np.array([0.6, 0.9])
p = net.predict(x)
t = np.array([0, 0, 1]) # 正确解标签
dW = numerical_gradient(f, net.W)
print(dW)

运行结果如下：
[[ 0.21924763 0.14356247 -0.36281009]
[ 0.32887144 0.2153437 -0.54421514]]

• $\frac{\partial L}{\partial w_{11}}$ 的值大约是 0.2，将 $w_{11}$ 增加 h，那么损失函数的值会增加 0.2h，所以应该向负向更新。
• $\frac{\partial L}{\partial w_{23}}$ 对应的值大约是 -0.5，将 $w_{23}$ 增加 h，损失函数的值将减小 0.5h，所以应该向正向更新，且贡献值比 $w_{11}$ 大。
• lambda表示函数法：

f = lambda w: net.loss(x, t)
dW = numerical_gradient(f, net.W)

4.5　学习算法的实现

本书介绍的神经网络学习步骤：

Created with Raphaël 2.2.0 开始 mini-batch 计算梯度 更新参数 是否达到梯度更新次数？ 结束 yes no

• 对于随机选择的mini batch数据，采用随机梯度下降法（stochastic gradient descent）。在深度学习的很多框架中，随机梯度下降法一般由一个名为 SGD 的函数来实现。

4.5.1　2 层神经网络的类

我们要实现为一个名为 TwoLayerNet 的类,代码在课程的ch04/two_layer_net.py里

import sys, os
sys.path.append(os.pardir)
from common.functions import *
from common.gradient import numerical_gradient

class TwoLayerNet:

    def __init__(self, input_size, hidden_size, output_size,
                 weight_init_std=0.01): #初始化时包含输入层的神经元数、隐藏层的神经元数、输出层的神经元数
        # 初始化权重函数
        self.params = {}
        self.params['W1'] = weight_init_std * \
                            np.random.randn(input_size, hidden_size) #高斯分布的随机数进行权重初始化
        self.params['b1'] = np.zeros(hidden_size)#偏置使用 0 进行初始化
        self.params['W2'] = weight_init_std * \
                            np.random.randn(hidden_size, output_size)
        self.params['b2'] = np.zeros(output_size)

    def predict(self, x): # 神经网络识别函数
        W1, W2 = self.params['W1'], self.params['W2']
        b1, b2 = self.params['b1'], self.params['b2']

        a1 = np.dot(x, W1) + b1
        z1 = sigmoid(a1)
        a2 = np.dot(z1, W2) + b2
        y = softmax(a2)

        return y

    # x:输入数据, t:监督数据
    def loss(self, x, t): #损失函数
        y = self.predict(x)

        return cross_entropy_error(y, t)

    def accuracy(self, x, t): #识别精度函数
        y = self.predict(x)
        y = np.argmax(y, axis=1) #取概率最大值
        t = np.argmax(t, axis=1) #取最大值标签

        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

    # x:输入数据, t:监督数据
    def numerical_gradient(self, x, t): #梯度函数
        loss_W = lambda W: self.loss(x, t)

        grads = {} #grads保存梯度的字典型变量
        grads['W1'] = numerical_gradient(loss_W, self.params['W1'])
        grads['b1'] = numerical_gradient(loss_W, self.params['b1'])
        grads['W2'] = numerical_gradient(loss_W, self.params['W2'])
        grads['b2'] = numerical_gradient(loss_W, self.params['b2'])

        return grads

所有的函数在之前的学习中都已经涉及到了，不再多做赘述。

4.5.2　mini-batch 的实现

使用 MNIST 数据集进行学习，代码在课程的ch04/train_neuralnet.py里

import numpy as np
from dataset.mnist import load_mnist
from two_layer_net import TwoLayerNet

(x_train, t_train), (x_test, t_test) = \ load_mnist(normalize=True, one_hot_
label = True)

train_loss_list = []

# 超参数
iters_num = 10000 #更新的循环次数
train_size = x_train.shape[0] #训练数据大小
batch_size = 100 #要选出的数据大小
learning_rate = 0.1 #学习率

network = TwoLayerNet(input_size=784, hidden_size=50, output_size=10)

for i in range(iters_num):
    # 获取mini-batch
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]

    # 计算梯度
    grad = network.numerical_gradient(x_batch, t_batch)
    # grad = network.gradient(x_batch, t_batch) # 误差反向传播法

    # 更新参数
    for key in ('W1', 'b1', 'W2', 'b2'):
        network.params[key] -= learning_rate * grad[key]

    # 记录学习过程
    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)

我们可以看到损失函数的值在循环中不断更新，越来越小，这是神经网络正在学习的信号，说明神经网络正在向最优参数拟合。

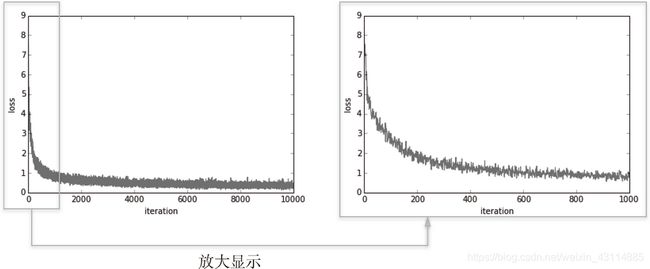
4.5.3　基于测试数据的评价

除了看损失函数的值这一个信号，还不能确定是否会发生过拟合，所以，我们采取的方法是，每经过一个 epoch，记录下训练数据和测试数据的识别精度。

• epoch：学习中所有训练数据均被使用过一次时的更新次数，在mini-batch中，我们抽取了100个数据，100就是一个epoch，10000次重复的更新中，每到100的倍数时就检验一次识别精度

在4.5.2的代码之上，我们增加以下代码：

train_acc_list = [] #训练数据识别精度数组
test_acc_list = [] #测试数据识别精度数组
# 平均每个epoch的重复次数
iter_per_epoch = max(train_size / batch_size, 1) #epoch大小
...
# 计算每个epoch的识别精度
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        test_acc = network.accuracy(x_test, t_test)
        train_acc_list.append(train_acc)#每次的识别精度加入到数组中
        test_acc_list.append(test_acc)
        print("train acc, test acc | " + str(train_acc) + ", " + str(test_acc))

结果得到的训练数据和测试数据的识别精度变化如下：

说明变化参数的过程中，两者识别精度都上升了，而且基本一致，没有发生过拟合现象。

end

• 原书为《深度学习入门 基于Python的理论与实现》作者：斋藤康毅
  人民邮电出版社
• 本文章是gitchat的《陆宇杰的训练营：15天共读深度学习》¹的课程读书笔记
• 本文章大量引用原书中的内容和训练营课程中的内容作为笔记

---

1. 《陆宇杰的训练营：15天共读深度学习》 ↩︎