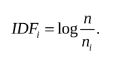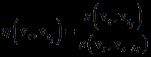回环检测之DBoW2
前面我们已经讲了回环检测中用的一些方法,今天主要介绍一下现在用的最多的词袋模型——DBoW2。这里就不在细讲回环检测的定义,具体可以看看我的前面的博客,而回环检测在SLAM中的作用可以从下面的图片中大致有一个了解。
左图是不存在回环功能的,当我们回到原来的地方的时候,由于累计误差导致了偏差,这在三维重建中特别明显,就是本来是一个矩形的空间建出来的奇形怪状了,当我们有了回环检测功能后,如右图,很大程度上与矩形空间相似。下图也是一样的,效果很明显。
1 词袋模型
现有的ORB-SLAM,VINS-mono等一些流行的slam框架几乎都是用词袋模型,词袋模型是一般采用离线数据集进行训练,然后构建词袋树,而SLAM在启动程序的时候预先加载这些词袋树,通过词袋树的信息,对特征进行匹配,从而得到图像的相似度,确定是否重定位成功或者回环成功。
词袋模型有很多种,一般有DBoW,DBoW2,DBoW3,fBoW,FAB-MAP。
1.1DBoW
DBow库是一个开源C ++库,用于索引图像并将图像转换为词袋表示。它实现了一个分层树,用于近似图像特征空间中的最近邻并创建可视词汇表。DBow还实现了一个基于逆序文件结构的图像数据库,用于索引图像和快速查询。DBow不需要OpenCV(演示应用程序除外),但它们完全兼容。
源码地址:https://github.com/dorian3d/DBow
1.2 DBoW2
DBoW2是DBow库的改进版本,DBoW2实现了具有正序和逆序指向索引图片的的图像数据库,可以实现快速查询和特征比较。与以前的DBow库的主要区别是:
1)DBoW2类是模板化的,因此它可以与任何类型的描述符一起使用。
2)DBoW2将直接文件添加到图像数据库以进行快速功能比较。
3)它使用OpenCV存储系统来保存词汇表和数据库。
4)已经重写了一些代码以优化速度。
DBoW2和DLoopDetector已经在几个真实数据集上进行了测试,执行了3毫秒,可以将图像的简要特征转换为词袋向量量,在5毫秒可以在数据库中查找图像匹配超过19000张图片。
源码地址:https://github.com/dorian3d/DBow2
1.3 DBoW3
DBoW3是DBow2库的改进版本,与以前的DBow2库的主要区别是:
1)DBoW3只需要OpenCV。DLIB的DBoW2依赖性已被删除。
2)DBoW3能够适用二进制和浮点描述符。无需为任何描述符重新实现任何类。
3)已经重写了一些代码以优化速度。
4)使用二进制文件。二进制文件加载/保存比yml快4-5倍。而且,它们可以被压缩。
5)兼容DBoW2的yml文件
源码地址:github.com/rmsalinas/DBoW3
1.4 FBoW
FBOW(Fast Bag of Words)是DBow2 / DBow3库的极端优化版本。该库经过高度优化,可以使用AVX,SSE和MMX指令加速Bag of Words创建。在加载词汇表时,fbow比DBOW2快约80倍(参见tests目录并尝试)。在使用具有AVX指令的机器上将图像转换为词袋时,它的速度提高了约6.4倍。
源码地址:github.com/rmsalinas/fbow
本篇重点介绍DBoW2原理以及代码,先用一幅图了解一下BoW
本文主要基于ORBSLAM2上使用的词袋进行介绍,ORB-SLAM2中的ORBvoc.txt是作者使用非常庞大的图片库生成的,对室内和户外都有很好的效果,有时候自己生成的字典,由于我们采集的图片质量以及数据集没有他们那么庞大,效果不一定会比作者提供的好。先来看一下ORBvoc.txt里面是什么样子的
第一行中10代表词袋树的分支,6代表树的深度,0,代表相似度,0代表权重。
第二行的0代表节点的父节点,第二个0代表是否叶子结点,这里表示非叶子结点,252-43表示特征,最后一个表示权重。
2 DBoW2代码解析和应用
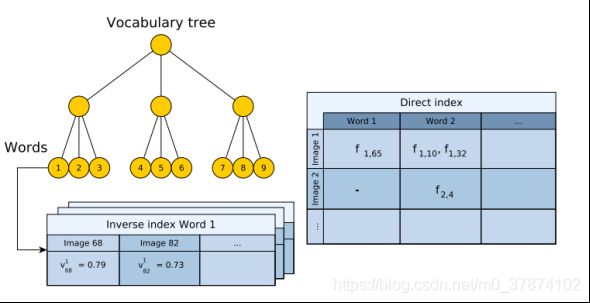
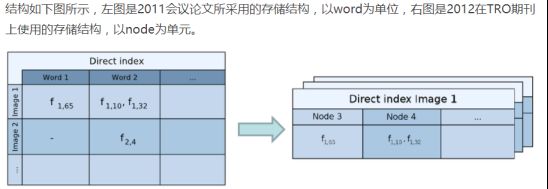
我们先来介绍一下词袋模型中涉及到的数据结构,如下图
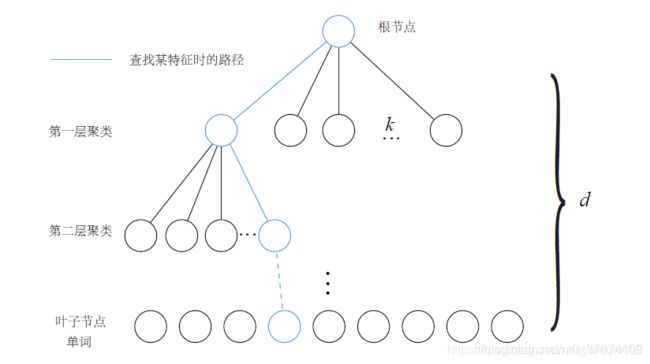
词袋中采用树的结构存储,为了方便回环检测的应用,正向索引和逆向索引两种结构。词袋树的结构下图
其中k为分支个数,d为树的深度。
每个节点的内容如下:
当两幅图像进行特征匹配时,如果极线约束未知,那么只有暴力匹配,复杂度为O(N2),或者先为特征生成k-d树再利用k-d树匹配,复杂度为O(NlogN)。作者提供了一种正向索引用于加速特征匹配。正向索引需要指定词典树中的层数,比如第m层。每幅图像对应一个正向索引,储存该图像生成BoW向量时曾经到达过的第m层上节点的编号,以及路过这个节点的那些特征的编号。正向索引的具体定义为:
// DirectFile为所有图像正向索引的集合
// 每个图像有一个FeatureVector,
typedef std::vector
// DirectFile[entry_id] --> [ node_id, vector
而FeatureVector结构如下:
class FeatureVector: public std::map<NodeId, std::vector<unsigned int> >
继承自std::map,NodeId为node节点的ID,其范围在[0, k^l)内,l表示当前层数(这里以最上层为0层),std::vector
图中的fn,m表示在第n帧图像中的第m个特征点的特征点。
逆向索引主要用来回环检测和重定位减少计算量的,结构示意图如下:
我们可以采用逆向索引,根据当前帧的图像中含有的描述子,去数据库中索引出所有含有该描述子的图片,并且根据权重进行挑选候选帧,从而实现重定位或者回环检测功能。优点在于不用计算数据库中所有图像于当前帧的相似,从而加速计算。其数据结构如下:
// InvertedFile为所有叶节点反向索引的集合
// 每个叶节点(word)有一个反向索引,定义为IFRow
typedef std::vector
// InvertedFile[word_id] --> inverted file of that word
// IFRow定义list,为一系列图像编号的集合
// IFRows根据图像编号的升序排列
typedef std::list
struct IFPair
{
// Entry id,图像编号
EntryId entry_id;
// Word weight in this entry,叶节点权重
WordValue word_weight;
}
基础的数据结构大致介绍完毕,接下来介绍一下DBoW2库
我们先来看一下DBoW2整个框架的流程图。
我们训练词袋模型一般有如下步骤:
1 读取我们采集的图片
2 对读取的所有图片进行描述子提取
3 构建词袋
4 检测词袋效果
代码如下:
int main()
{
vector > features;
//加载图片
string pathTimeStamps = "/home/sources/Examples/Monocular/EuRoC_TimeStamps/MH01.txt";
string pathCam0 = "/home/datasets/EuRoC/MH01/mav0/cam0/data";
vector vstrImageFilenames;
vector vTimestampsCam;
LoadImages(pathCam0, pathTimeStamps, vstrImageFilenames, vTimestampsCam);
NIMAGES = vstrImageFilenames.size();
loadFeatures(features,vstrImageFilenames);
testVocCreation(features);
wait();
testDatabase(features);
return 0;
} 其中LoadImages函数如下:
void LoadImages(const string &strImagePath, const string &strPathTimes,
vector &vstrImages, vector &vTimeStamps)
{
ifstream fTimes;
cout << "path "<< strPathTimes<> t;
vTimeStamps.push_back(t / 1e9);
}
}
} 读取全部图片,进行特征提取。提取函数如下:
void loadFeatures(vector > &features, vector& vstrImageFilenames)
{
// 放置描述子
features.clear();
features.reserve(NIMAGES );
//创建orb
cv::Ptr orb = cv::ORB::create();
cout << "Extracting ORB features..." << endl;
for(int i = 0; i < NIMAGES; ++i)
{
// stringstream ss = vstrImageFilenames[i];
string ss = vstrImageFilenames[i];
cout << " i "< keypoints;
cv::Mat descriptors;
//提取orb特征点以及描述子
orb->detectAndCompute(image, mask, keypoints, descriptors);
features.push_back(vector());
//描述子转换
changeStructure(descriptors, features.back());
}
} 其中,changeStructure函数如下:
void changeStructure(const cv::Mat &plain, vector &out)
{
out.resize(plain.rows);
for (int i = 0; i < plain.rows; ++i)
{
out[i] = plain.row(i);
}
} 创建词袋接口如下:
void testVocCreation(const vector > &features)
{
// branching factor and depth levels
const int k = 10;// kd树的分支
const int L = 5;// kd树的层数
const WeightingType weight = TF_IDF;// 权值计算方式
const ScoringType scoring = L1_NORM;// 计算分数的方法
OrbVocabulary voc(k, L, weight, scoring);//初始化词袋
cout << "Creating a small " << k << "^" << L << " vocabulary..." << endl;
voc.create(features);//将前面提取的全部特征点存入词袋中
cout << "... done!" << endl;
cout << "Vocabulary information: " << endl
<< voc << endl << endl;
// lets do something with this vocabulary
cout << "Matching images against themselves (0 low, 1 high): " << endl;
BowVector v1, v2;
for(int i = 0; i < NIMAGES; i++)
{
voc.transform(features[i], v1);//将图像描述子转成词袋中的数据结构BoW
for(int j = 0; j < NIMAGES; j++)
{
voc.transform(features[j], v2);
double score = voc.score(v1, v2);//计算两帧之间的得分
cout << "Image " << i << " vs Image " << j << ": " << score << endl;
}
}
// save the vocabulary to disk
cout << endl << "Saving vocabulary..." << endl;
// voc.save("small_voc.yml.gz");
voc.saveToTextFile("MyVoc.txt");
voc.saveToBinaryFile("myVoc.bin");
cout << "Done" << endl;
} 上面的代码大致讲述了词袋的形成,但是具体的没有细说,接下来我们讲一下怎么训练出词袋模型。在本文的前面,已经有说过,词袋的数据结构采用树的结构,这里先要说明一下为什么需要用到树的结构,因为,我们训练的数据集大致需要10000以上的图片,每张图片提取的特征点大致有500个,那么至少有5000000个描述子,每个描述子256维,如果你从这么庞大的数据中去一一对比和你相似的描述子,显然不太现实,因此,采用树的结构,减少了大量的查找计算,加快匹配速度。
那么采用什么方法构建词袋树呢?,DBoW2采用Kmeans++聚类方法,也就是最核心的方法。
聚类是机器学习、计算几何的经典问题。而K-Means算法是无监督的聚类算法中的应用比较普遍,它实现起来比较简单,聚类效果也不错,因此应用很广泛。K-Means算法有大量的变体,本文就从最传统的K-Means算法从而引出K-means++算法
k-means算法原理简单、容易实现,计算时间短、速度快,但精度不够高。
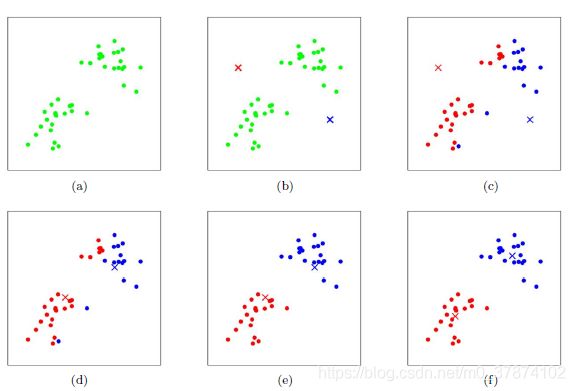
K-Means采用的启发式方式很简单,用下面一组图就可以形象的描述。
上图a表达了初始的数据集,假设k=2。在图b中,我们随机选择了两个k类所对应的类别质心,即图中的红色质心和蓝色质心,然后分别求样本中所有点到这两个质心的距离,并标记每个样本的类别为和该样本距离最小的质心的类别,如图c所示,经过计算样本和红色质心和蓝色质心的距离,我们得到了所有样本点的第一轮迭代后的类别。此时我们对我们当前标记为红色和蓝色的点分别求其新的质心,如图4所示,新的红色质心和蓝色质心的位置已经发生了变动。图e和图f重复了我们在图c和图d的过程,即将所有点的类别标记为距离最近的质心的类别并求新的质心。最终我们得到的两个类别如图f。
由此可得出一般的K-Means算法流程
输入是样本集D={x1,x2,...xm},聚类的簇树k,最大迭代次数N
输出是簇划分C={C1,C2,...Ck}
1) 从数据集D中随机选择k个样本作为初始的k个质心向量: {μ1,μ2,...,μk}
2)对于n=1,2,...,N
a) 将簇划分C初始化为Ct=∅t=1,2...k
b) 对于i=1,2...m,计算样本xi和各个质心向量μj(j=1,2,...k)的距离:dij=||xi−μj||22,将xi标记最小的为dij所对应的类别λi。此时更新Cλi=Cλi∪{xi}
c) 对于j=1,2,...,k,对Cj中所有的样本点重新计算新的质心μj=1|Cj|∑x∈Cjx
e) 如果所有的k个质心向量都没有发生变化,则转到步骤3)
3) 输出簇划分C={C1,C2,...Ck}
k-means算法以欧式距离作为距离或相似度测算,求对应的初始聚类中心数据的最优分类,使得评价结果最小。算法采用误差平方和准则函数作为聚类准则函数。
而什么是K-Means++呢
k个初始化的质心的位置选择对最后的聚类结果和运行时间都有很大的影响,因此需要选择合适的k个质心。如果仅仅是完全随机的选择,有可能导致算法收敛很慢。K-Means++算法就是对K-Means随机初始化质心的方法的优化。
K-Means++的对于初始化质心的优化策略也很简单,如下:
a) 从输入的数据点集合中随机选择一个点作为第一个聚类中心μ1
b) 对于数据集中的每一个点xi,计算它与已选择的聚类中心中最近聚类中心的距离D(xi)=argmin||xi−μr||22r=1,2,...kselected
c) 选择一个新的数据点作为新的聚类中心,选择的原则是:D(x)较大的点,被选取作为聚类中心的概率较大
d) 重复b和c直到选择出k个聚类质心
e) 利用这k个质心来作为初始化质心去运行标准的K-Means算法
k-means++的源码如下:
templatevoid TemplatedVocabulary::HKmeansStep
(
NodeId parent_id, // 父节点id
const std::vector &descriptors, // 该父节点对应的特征描述集合
int current_level // 当前层数
)
{
if (descriptors.empty()) return;
// 用来存储子节点的特征描述 features associated to each cluster
std::vector clusters;
// 用来存储每个子节点对应的特征描述在descriptors向量中的id
std::vector > groups; // groups[i] = [j1, j2, ...]
// j1, j2, ... indices of descriptors associated to cluster i
clusters.reserve(m_k);
groups.reserve(m_k);
// 如果特征描述个数小于m_k,直接分类
if ((int)descriptors.size() <= m_k) {
// trivial case: one cluster per feature
groups.resize(descriptors.size());
for (unsigned int i = 0; i < descriptors.size(); i++) {
groups[i].push_back(i);
clusters.push_back(*descriptors[i]);
}
} else {
// k-means分类
bool first_time = true;
bool goon = true;
// 用于检查迭代过程中前后两次分类结果是否一致,如一致,分类结束
std::vector last_association, current_association;
// 迭代过程
while (goon) {
// 1. 分类
if (first_time) {
// 第一次,初始化分类
initiateClusters(descriptors, clusters);
} else {
// 计算每一类的meanValue
for (unsigned int c = 0; c < clusters.size(); ++c) {
std::vector cluster_descriptors;
cluster_descriptors.reserve(groups[c].size());
// 利用group,读取每一类对应的id
std::vector::const_iterator vit;
for (vit = groups[c].begin(); vit != groups[c].end(); ++vit) {
cluster_descriptors.push_back(descriptors[*vit]);
}
// 计算meanValue
F::meanValue(cluster_descriptors, clusters[c]);
}
} // if(!first_time)
// 2. 利用1计算的中心重新分类
groups.clear();
groups.resize(clusters.size(), std::vector());
current_association.resize(descriptors.size());
typename std::vector::const_iterator fit;
// 对每一个特征,计算它与K个中心特征的距离,标记距离最小的中心特征的id
for (fit = descriptors.begin(); fit != descriptors.end(); ++fit) { //, ++d)
//计算欧式距离
double best_dist = F::distance(*(*fit), clusters[0]);
unsigned int icluster = 0;
for (unsigned int c = 1; c < clusters.size(); ++c) {
double dist = F::distance(*(*fit), clusters[c]);
if (dist < best_dist) {
best_dist = dist;
icluster = c;
}
}
// 记录分类信息
groups[icluster].push_back(fit - descriptors.begin());
current_association[ fit - descriptors.begin() ] = icluster;
}
// kmeans++ ensures all the clusters has any feature associated with them
// 3. 检查前后两次分类结果是否一致,如一致,分类结束
if (first_time) {
first_time = false;
} else {
goon = false;
for (unsigned int i = 0; i < current_association.size(); i++) {
if (current_association[i] != last_association[i]) {
goon = true;
break;
}
}
}
// 如果不一致,存储本次分类信息
if (goon) {
// copy last feature-cluster association
last_association = current_association;
}
} // while(goon)
} // if must run kmeans
// 生成本层的节点,其特征描述为每一类的meanValue
for (unsigned int i = 0; i < clusters.size(); ++i) {
NodeId id = m_nodes.size();
m_nodes.push_back(Node(id));
m_nodes.back().descriptor = clusters[i];
m_nodes.back().parent = parent_id;
m_nodes[parent_id].children.push_back(id);
}
// 如果没有达到L层,继续分类
if (current_level < m_L) {
// iterate again with the resulting clusters
const std::vector &children_ids = m_nodes[parent_id].children;
for (unsigned int i = 0; i < clusters.size(); ++i) {
// 当前层的节点id
NodeId id = children_ids[i];
std::vector child_features;
child_features.reserve(groups[i].size());
std::vector::const_iterator vit;
// 该id对应的特征描述集合
for (vit = groups[i].begin(); vit != groups[i].end(); ++vit) {
child_features.push_back(descriptors[*vit]);
}
// 进入下一层,继续分类
if (child_features.size() > 1) {
HKmeansStep(id, child_features, current_level + 1);
}
}
}
} 可以看出,词典树的所有节点是按照层数来排列的。假设这棵树有K类L层,则树里面总共有1+K+⋯+KL=(KL+1−1)/(K−1)个节点。所有节点在最底层形成了KL个子节点,每一类用该类中所有特征的平均特征(meanValue)作为代表,称为单词(word)。每个叶节点被赋予一个权重。作者提供了TF、IDF、BINARY、TF-IDF等权重作为备选,默认为TF-IDF。
TF-IDF的主要思想是:如果某个词或短语在一篇文章中出现的频率TF高,并且在其他文章中很少出现,则认为此词或者短语具有很好的类别区分能力,适合用来分类。TF-IDF实际上是TF * IDF,TF代表词频(Term Frequency),表示词条在文档d中出现的频率,假设图像M中单词wi出现了ni次,而一共出现的单词次数为n,则TFi计算公式如下:
![]() 转存失败重新上传取消
转存失败重新上传取消![]() 转存失败重新上传取消
转存失败重新上传取消
由以上公式也可看出,某单词在一幅图像中经常出现,它的区分度就越高。
IDF代表逆向文件频率(Inverse Document Frequency)。我们统计某个叶子节点wi中的特征数量相对于所有特征数量的比例作为IDF部分。假设所有特征数量为n,wi数量为ni,那么该单词的IDFi为:
![]() 转存失败重新上传取消
转存失败重新上传取消![]() 转存失败重新上传取消
转存失败重新上传取消
若IDFi=0,则表示该word的权重为0,即每张图片上都有该word。若IDFi≠0,则我们希望该word在当前图像中出现的概率越高越好,那样就会有更好地区分度。
于是,单词wi的权重weightingType等于TF乘IDF之积
TF-IDFi=TFi∗IDFi
在训练中只计算和保存单词的IDF值,即单词在众多图像中的区分度。TF则是从实际图像中计算得到各个单词的频率。单词的TF越高,说明单词在这幅图像中出现的越多;单词的IDF越高,说明单词本身具有高区分度。二者结合起来,即可得到这幅图像的BoW描述。
生成词典的代码如下:
templatevoid TemplatedVocabulary::create(
const std::vector > &training_features, // 图像特征集合
int k, // 每层的类的个数
int L, // 树的层数
WeightingType weighting, // 权重的类型,默认为TF-IDF
ScoringType scoring) // 得分的类型,默认为L1-norm
{
m_nodes.clear();
m_words.clear();
// 节点数 = Sum_{i=0..L} ( k^i )
int expected_nodes = (int)((pow((double)m_k, (double)m_L + 1) - 1)/(m_k - 1));
m_nodes.reserve(expected_nodes); // avoid allocations when creating the tree
// 将所有特征描述集合到一个vector
std::vector features;
getFeatures(training_features, features);
// 生成根节点
m_nodes.push_back(Node(0)); // root
// k-means++(内有递归)
HKmeansStep(0, features, 1);
// 建立一个只有叶节点的序列m_words
createWords();
// 为每个叶节点生成权重,此处计算IDF部分,如果不用IDF,则设为1
setNodeWeights(training_features);
} 生成词典的目的在于用这个先验信息在线的进行图像识别或者场景识别。当进来一帧时,怎么判断这帧图像和历史图像相似呢?一般分为两个步骤:
第一步:为图像生成一个表征向量v1×W。图像中的每个特征都在词典中搜索其最近邻的叶节点。所有叶节点上的权重集合构成了BoW向量v。
第二步:根据BoW向量,计算当前图像和其它图像之间的距离s(v1,v2)
注:L1-score指的是一范数得分,后面的绝对值也指的是求取一范数,最后得到的是一个标量。
s即为得分,差异越大得分越小趋近于0;相似则趋近于1 。这里只选用一种计算得分方法,实际上有很多种,具体可以看一下代码。通过判断得分来决定是否启动回环检测计算。为了保证回环检测的准确性,这里还需要加上很多约束,例如:组匹配,连续一致性,几何一致性等等,这个后面在涉及。
这里大概先讲一下如何检测相似图片,这里类似orbslam2。
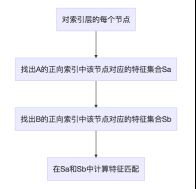
假设两幅图像为A和B,下图说明如何利用正向索引来加速特征匹配的计算。
注意到,正向索引的层数如果选择第0层(根节点),那么时间复杂度和暴力搜索一样。如果是叶节点层,则搜索范围有可能太小,错失正确的特征点匹配。作者一般选择第二层或者第三层作为父节点(L=6)。正向索引的复杂度约为O(N2/Km)。
图像转化为BoW向量(包含正向索引)
templatevoid TemplatedVocabulary::transform
(
const std::vector &features, // 图像特征集合
BowVector &v, // bow向量,std::map
FeatureVector &fv, // 正向索引向量,std::map
int levelsup // 正向索引的层数=L-levelsup
) const
{
// ignore some unimportant code here
// whether a vector must be normalized before scoring according
// to the scoring scheme
LNorm norm;
bool must = m_scoring_object->mustNormalize(norm);
typename std::vector::const_iterator fit;
// 依据权重类型,bow向量加入权重的方式有所不同
if (m_weighting == TF || m_weighting == TF_IDF) {
unsigned int i_feature = 0;
for (fit = features.begin(); fit < features.end(); ++fit, ++i_feature) {
WordId id;
NodeId nid;
WordValue w;
// 如果权重类型为TF-IDF,w为IDF。如为TF,w为1
transform(*fit, id, w, &nid, levelsup);
// 加入权重
if (w > 0) { // not stopped
// 累积该叶节点的idf权重,v(id).weight += w
// 最后v(id).weight实际上等于M*idf,M为插入该叶节点的特征描述的个数
v.addWeight(id, w);
// 插入
fv.addFeature(nid, i_feature);
}
}
if (!v.empty() && !must) {
// unnecessary when normalizing
const double nd = v.size();
// 只有SCORING_CLASS=DotProductScoring时
for (BowVector::iterator vit = v.begin(); vit != v.end(); vit++)
vit->second /= nd;
}
} else { // IDF || BINARY
unsigned int i_feature = 0;
for (fit = features.begin(); fit < features.end(); ++fit, ++i_feature) {
WordId id;
NodeId nid;
WordValue w;
// 如果权重类型为IDF,w为IDF。如为BINARY,w为1
transform(*fit, id, w, &nid, levelsup);
if (w > 0) { // not stopped
// 插入该叶节点的权重,v.insert(id,w)
v.addIfNotExist(id, w);
// 插入
fv.addFeature(nid, i_feature);
}
}
} // if m_weighting == ...
// 归一化bow向量,v=v/|v|
// 因为要归一化,所以之前计算的TF-IDF并没有除以TF的分母(特征的总数,对于bow向量中的所有项都相等)
if (must) v.normalize(norm);
} 单个图像特征寻找叶节点
templatevoid TemplatedVocabulary::transform
(
const TDescriptor &feature, // 当前带插入的特征描述
WordId &word_id, // 待取出的叶节点id(叶节点序列中的id,非树中的id)
WordValue &weight, // 待取出的权重
NodeId *nid, // 该特征描述对应的正向索引(树中某一层的父节点id)
int levelsup // 正向索引在第(L-levelsup)层上
) const
{
// 将当前特征描述插入词典树的叶节点层
std::vector nodes;
typename std::vector::const_iterator nit;
// 如果nid不为空,则nid储存该特征在第(L-levelsup)层上的父节点
// 用于正向指标
const int nid_level = m_L - levelsup;
if (nid_level <= 0 && nid != NULL) *nid = 0; // root
NodeId final_id = 0; // root
int current_level = 0;
// 逐层插入,直到叶节点层
do {
++current_level;
nodes = m_nodes[final_id].children;
final_id = nodes[0];
// 计算该特征与本层节点的距离,选取距离最小的节点
double best_d = F::distance(feature, m_nodes[final_id].descriptor);
for (nit = nodes.begin() + 1; nit != nodes.end(); ++nit) {
NodeId id = *nit;
double d = F::distance(feature, m_nodes[id].descriptor);
if (d < best_d) {
best_d = d;
final_id = id;
}
}
// 存储正向索引nid
if (nid != NULL && current_level == nid_level)
*nid = final_id;
} while ( !m_nodes[final_id].isLeaf() );
// 取出叶节点对应的word id(所有叶节点集合内的编号)和权重
word_id = m_nodes[final_id].word_id;
weight = m_nodes[final_id].weight;
}
权重更新过程
// 每幅图像有一个BoWVector// TF-IDF或者TF采用这个函数// 累积节点权重,bow向量是一个按WordId排序的有序序列void BowVector::addWeight(WordId id, WordValue v){
// 找到第一个大于等于id的节点
BowVector::iterator vit = this->lower_bound(id);
// 找到了输入id对应的节点
// 权重+=v
if(vit != this->end() && !(this->key_comp()(id, vit->first)))
{
vit->second += v;
}
// 没有找到输入id,插入
// vit==end()(id比现有WordId都大)
// 或者vit的id不等于输入的id
else
{
this->insert(vit, BowVector::value_type(id, v));
}
}// IDF或者BINARY采用这个函数// 当id不存在时,插入// 因为不考虑词频,所以每个叶节点只需要插入第一个到达此节点的权重值void BowVector::addIfNotExist(WordId id, WordValue v){
BowVector::iterator vit = this->lower_bound(id);
if(vit == this->end() || (this->key_comp()(id, vit->first)))
{
this->insert(vit, BowVector::value_type(id, v));
}
} FeatureVector更新过程
// 储存所有到达过某个node_id的feature_id(正向索引)// 每幅图像有一个FeatureVectorvoid FeatureVector::addFeature(NodeId id, unsigned int i_feature){
// 找到第一个key大于等于node_id的项
FeatureVector::iterator vit = this->lower_bound(id);
// 如果key==node_id,push_back
if(vit != this->end() && vit->first == id)
{
vit->second.push_back(i_feature);
}
// 如果id还没有出现,插入
else
{
vit = this->insert(vit, FeatureVector::value_type(id,
std::vector() ));
vit->second.push_back(i_feature);
}
} 前面部分已经大致讲述了SLAM中回环检测检测相似图像的基本原理,接下来讲述一下确定回环的基本原理,由于回环在SLAM中是非常重要的,如果检测到回环能够较小累计误差,如果检测到错误的回环,那么整个SLAM将是灾难性的错误。
根据之前的描述,两幅图像会根据特征点的描述子,转化成词袋中的数据结构,再利用这里结构进行计算分数:
但是这个分数可能因为特征点的位置不同,导致了同一张图片特征点不同,计算出来的分数也不一样,这种情况下,为了保证鲁棒性又添加了几个约束。
通过逆向索引,将上面得到的得分进一步归一化:
其中s(vt,vt−δt)为t时刻图像与t−Δt时刻图像的得分。当相机旋转很快时,分母会偏小,η会偏大,因此还要规定一个最小的s(vt,vt−Δt),默认值为0.005。另外,η也需要达到一个最小值,默认值为0.3。这里采用逆向索引的目的是只匹配包含相同单词的个别图像信息, 加快检索过程。
这里我们会过滤掉一部分的候选回环帧。(orbslam2采用的是另一种方法)保留符合要求的候选图像进入组匹配进行校验。
由于相邻两幅候选图像与当前图像的得分会很接近。为了选取更具代表性的图像,作者根据图像id(即时间顺序)对候选图像进行分组,计算和比较组间的得分,从而避免在小时间段内重复选取。定义一组(island)的得分为:
当图像 It,It′,表示了一个真正的回环,则It 同样也和It±Δt,It±2Δt 有着较高的相似性,定义相似得分和函数如下:
其中VTi 表示候选图像所在集合从Vtni 到 Vtmi
1、防止连续图像在数据库查询时存在的竞争关系,但是不会考虑同一地点,不同时间的关键帧。
2、防止误匹配
当一个真正的回环出现时,回环附近的图像与当前图像的相似度都会比较高,因此计算累积得分能更好地区分出回环图像。最后,选取得分最高的分组VT′。
找到最好的分组后,还要检查在一定时间内回环是否稳定存在。假设t时刻出现一个真正的回环,那么在接下来的一定时间内,回环应当是稳定存在的。因此,回环应该在时间上具有一致性。具体而言,vt+kδt时刻应该也检测出一个回环VT′k,并且和VT′很接近(指组内的图像序列编号),k=1,⋯,K。如果回环在K个时刻都满足一致性,那么认为这是一个好的回环检测。默认参数K=3。
选定了回环图像后,作者还检查了两幅图像之间的几何一致性。通过计算两幅图像之间的基本矩阵(fundamental matrix),判断其内点数是否足够(作者选择的阈值是12)。如果不够,说明两幅图像之间的特征匹配并不可靠,予以拒绝。
至此,整个回环检测的流程已经结束了 。
这里推荐开源代码DLoopDetector亲自验证一下。