深度学习笔记（1）（CNN）

1.Loss损失函数的作用

• 损失函数用来评价模型的预测值和真实值不一样的程度，深度学习训练模型的时候就是通过计算损失函数，更新模型参数，从而减小优化误差，直到损失函数值下降到目标值 或者 达到了训练次数。
• 均方误差mean squareerror（MSE）：MSE表示了预测值与目标值之间差值的平方和然后求平均。每个样本的平均平方损失。MSE的计算方法是平方损失除以样本数。
• 一种衡量指标，用于衡量模型的预测偏离其标签程度。要确定此值，模型需要定义损失函数。例如：线性回归模型参与均方误差MSE损失函数，分类模型采用交叉熵损失函数。

 

• L2范数：L2损失表示了预测值与目标值之间差值的平方和然后开更方，L2表示的是欧几里得距离。

 

• 平均绝对误差meanabsolute error(MAE )：MAE表示了预测值与目标值之间差值的绝对值然后求平均

 

反向传播算法（backpropagation）

该算法会先按前向传播方式计算（并缓存）每个节点的输出值，然后再按反向传播遍历图的方式计算损失函数值相对于每个参数的偏导数。

批次（batch）

模型训练的一次迭代（一次梯度更新）中使用的样本集。

批次大小（batch size）

一个批次中的样本数。比如，在随机梯度下降SGD算法中，批次大小为1；在梯度下降算法中，批次大小为整个训练集；

批量梯度下降算中，批次大小可以自定义的，通常取值范围是10到1000之间。比如：训练集为40000个样本，设置批次大小为32，训练一次模型，使用到32个样本。

随机梯度下降（SGD）

梯度下降法在大数据集，会出现费时、价值不高等情况。如果我们可以通过更少的计算量得出正确的平均梯度，效果更好。通过从数据集中随机选择样本，来估算出较大的平均值。

原理  它每次迭代只使用一个样本（批量大小为1）。

如果进行足够的迭代，SGD也可以发挥作用，但过程会非常杂乱。“随机”这一术语表示构成各个批量的一个样本都是随机选择的。
 

批量梯度下降法（BGD）

它是介于全批量迭代与随机选择一个迭代的折中方案。全批量迭代（梯度下降法）；随机选择一个迭代（随机梯度下降）。

原理  它从数据集随机选取一部分样本，形成小批量样本，进行迭代。小批量通常包含10-1000个随机选择的样本。BGD可以减少SGD中的杂乱样本数量，但仍然波全批量更高效。
 

检查gpu：

torch.cuda.device_count() 

卷积神经网络CNN

https://andyguo.blog.csdn.net/article/details/120710054

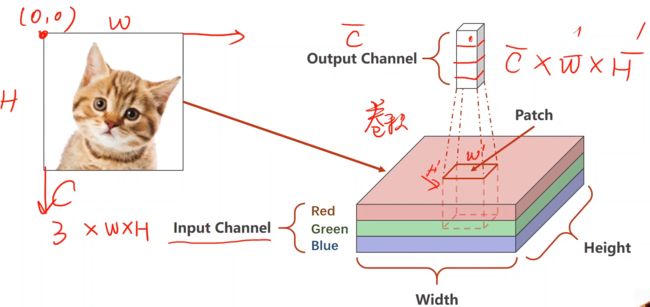
明确输入的张量维度和输出的张量维度，设计维度上的变化，最终映射到我们想要的空间上。

卷积层每次需要拿出一块像素块进行操作

 定义一个卷积层：输入通道数、输出通道数、卷积核的大小（长和宽）。

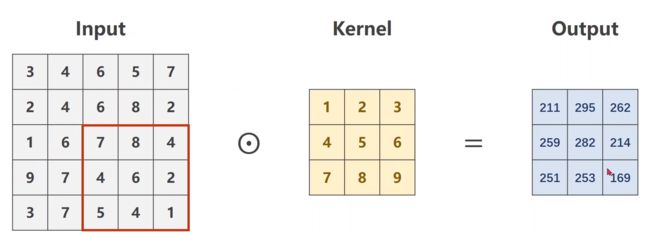
2.1 单通道卷积运算

 2.1 单通道卷积运算

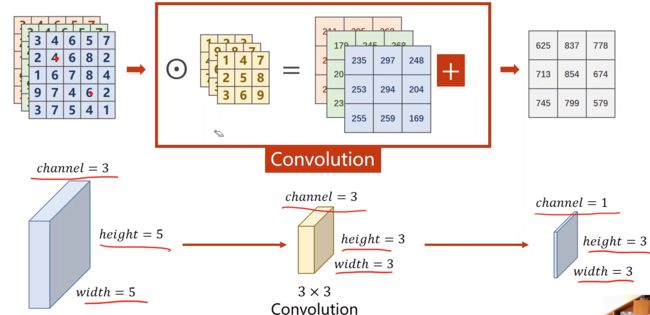
 一开始input的彩色图像的通道是3，到中间的网络可能有几百个通道数，下面以三通道卷积为例，注意卷积核数 = 通道数。

 

如果输入是n个通道：

 如果要有m个输出channel，就要使用m个卷积核：

（1）每个卷积核的通道数要求和输入通道相同；
（2）卷积核的组数是和输出的通道数相同；
（3）卷积核的大小由自己来定，和图像的大小无关，一般设置为正方形，边长为奇数（其实设置为长方形也是可以的）。

 2.3 卷积层

 中间红色字体即每个卷积核的size

# -*- coding: utf-8 -*-
"""
Created on Tue Oct 12 09:07:16 2021

@author: 86493
"""
import torch
in_channels, out_channels = 5, 10
width, height = 100, 100
kernel_size = 3 # 3×3的卷积核
batch_size = 1

# 定义了input张量的维度，但具体的值randn(标准均匀分布)
input = torch.randn(batch_size,
                    in_channels,
                    width,
                    height)

conv_layer = torch.nn.Conv2d(in_channels,
                             out_channels, 
                             kernel_size = kernel_size)

output = conv_layer(input)

print(input.shape)
# 打印出torch.Size([1, 5, 100, 100])
# 即5个通道，100×100图像
print(output.shape)
# 打印出torch.Size([1, 10, 98, 98])
# 输出为10个通道，98×98图像，100-2（3-1=2）
print(conv_layer.weight.shape)
# torch.Size([10, 5, 3, 3])
# 卷积层权重的形状，输出的通道为10，输入的通道为5，
# 卷积核大小为3×3

卷积层和池化层对【输入图像的维度大小】没有要求（对输入的通道数有要求，如上面输入的channel为6则出错），最后的分类器最在乎。

 因为最后要用交叉熵损失，所有最后一层是不用激活的。

三、重要参数介绍

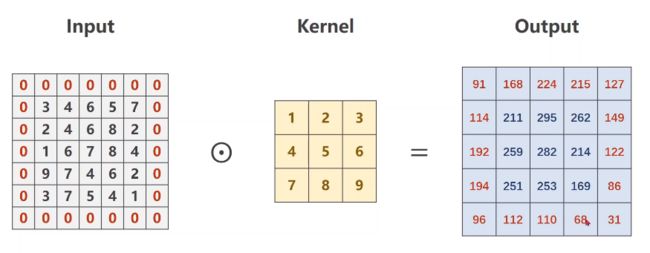
3.1 padding详解

做padding时，如果卷积核是3×3就填充1圈，如果是5×5就填充2圈（圈数也可按下图绿色框规律，即做整除）。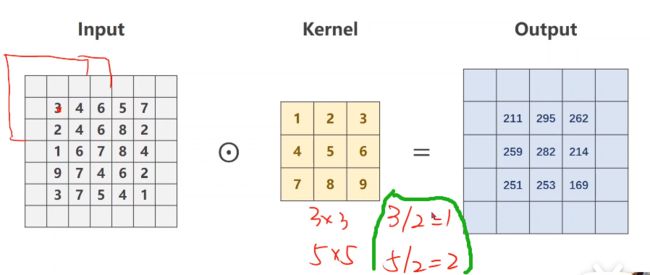

 我们在原始的input外面一层填充0后，做卷积后的结果：

# -*- coding: utf-8 -*-
"""
Created on Tue Oct 12 09:52:08 2021

@author: 86493
"""
import torch

input = [3, 4, 6, 5, 7,
         2, 4, 6, 8, 2,
         1, 6, 7, 8, 4,
         9, 7, 4, 6, 2,
         3, 7, 5, 4, 1]
input = torch.Tensor(input).view(1, 1, 5, 5)
# batch=1,channel=1,size=5×5

# 输入通道为1，输出通道为1
conv_layer = torch.nn.Conv2d(1, 1, 
                             kernel_size = 3,
                             padding = 1,
                             bias = False)
# 不给通道量加bias，所以设置为false

# 输出通道数=1，输入通道数=1
kernel = torch.Tensor([1, 2, 3, 4, 5, 6, 7, 8,
                       9]).view(1, 1, 3, 3)

conv_layer.weight.data = kernel.data
# 赋值给卷积层的权重

output = conv_layer(input)
print(output)

3.2 stride详解

修改步长stride，可以有效地降低图像宽度和高度，如我们直接修改上面3.1代码（增加stride=1）

# -*- coding: utf-8 -*-
"""
Created on Tue Oct 12 09:52:08 2021

@author: 86493
"""
import torch

input = [3, 4, 6, 5, 7,
         2, 4, 6, 8, 2,
         1, 6, 7, 8, 4,
         9, 7, 4, 6, 2,
         3, 7, 5, 4, 1]
input = torch.Tensor(input).view(1, 1, 5, 5)
# batch=1,channel=1,size=5×5

# 输入通道为1，输出通道为1
conv_layer = torch.nn.Conv2d(1, 1, 
                             kernel_size = 3,
                             stride = 2,
                             bias = False)
# 不给通道量加bias，所以设置为false

# 输出通道数=1，输入通道数=1
kernel = torch.Tensor([1, 2, 3, 4, 5, 6, 7, 8,
                       9]).view(1, 1, 3, 3)

conv_layer.weight.data = kernel.data
# 赋值给卷积层的权重

output = conv_layer(input)
print(output)
# tensor([[[[211., 262.],
#          [251., 169.]]]], grad_fn=)

3.3 nn.Conv2d详解

这块主要将CNN的通道channel。

1）pytorch的二维卷积方法nn.Conv2d用于二维图像。

class torch.nn.Conv2d(in_channels,
	out_channels, kernel_size, stride=1, padding=0, dilation=1, groups=1,
	bias=True)

dilation:控制 kernel 点之间的空间距离

groups:分组卷积

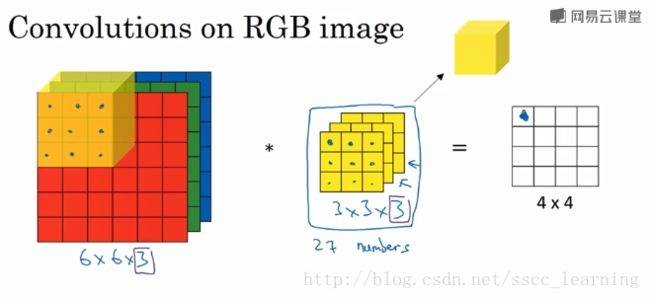
如下图，假设现有一个为 6×6×3 的图片样本，使用 3×3×3 的卷积核（filter）进行卷积操作。此时输入图片的 channels 为 3 ，而卷积核中的 in_channels 与 需要进行卷积操作的数据的 channels 一致（这里就是图片样本，为3）。

 接下来，进行卷积操作，卷积核中的27个数字与分别与样本对应相乘后，再进行求和，得到第一个结果。依次进行，最终得到 4×4 的结果。

 上面步骤完成后，由于只有一个卷积核，所以最终得到的结果为 4×4×1 ， out_channels 为 1 。

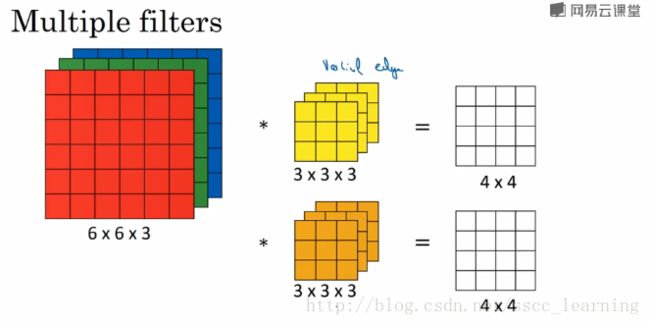
在实际应用中，都会使用多个卷积核。这里如果再加一个卷积核，就会得到 4×4×2 的结果。

• 最初输入的图片样本的 channels ，取决于图片类型，比如RGB；

• 卷积操作完成后输出的 out_channels ，取决于卷积核的数量。此时的 out_channels 也会作为下一次卷积时的卷积核的 in_channels；
• 卷积核中的 in_channels ，刚刚2中已经说了，就是上一次卷积的 out_channels ，如果是第一次做卷积，就是1中样本图片的 channels 。

四、池化层

4.1 最大池化

通道数不变，图像大小缩小，pytorch中用的是MaxPool2d。

 五 完整cnn例子

# -*- coding: utf-8 -*-
"""
Created on Tue Oct 19 15:02:11 2021

@author: 86493
"""
import torch 
import torch.nn as nn
from torchvision import transforms
from torchvision import datasets 
from torch.utils.data import DataLoader
import torch.nn.functional as F
import torch.optim as optim 
import matplotlib.pyplot as plt 

# 准备数据
batch_size = 64
transform = transforms.Compose([transforms.ToTensor(),
                                transforms.Normalize((0.1307,), (0.3081))])
train_dataset = datasets.MNIST(root = '../dataset/mnist/', 
                               train = True,
                               download = True,
                               transform = transform)
train_loader = DataLoader(train_dataset,
                          shuffle = True,
                          batch_size = batch_size)
test_dataset = datasets.MNIST(root = '../dataset/mnist/',
                              train = False,
                              download = True,
                              transform = transform)
test_loader = DataLoader(test_dataset,
                         shuffle = False,
                         batch_size = batch_size)

# CNN网络
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 10, kernel_size = 5)
        self.conv2 = nn.Conv2d(10, 20, kernel_size = 5)
        self.pooling = nn.MaxPool2d(2)
        self.fc = nn.Linear(320, 10)
        
    def forward(self, x):
        # Flatten data from (n, 1, 28, 28)to(n, 784)
        batch_size = x.size(0)
        x = F.relu(self.pooling(self.conv1(x)))
        x = F.relu(self.pooling(self.conv2(x)))
        # flatten
        x = x.view(batch_size, -1)
        # print("x.shape", x.shape)
        x = self.fc(x)
        return x
    
model = Net()
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# 有多个显卡时则可以填其他cuda号
model.to(device)
# 把模型的参数等放到显卡中

# 设计损失函数和优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(model.parameters(),
                      lr = 0.01,
                      momentum = 0.5)

def train(epoch):
    running_loss = 0.0 
    for batch_idx, data in enumerate(train_loader, 0):
        # 1.准备数据
        inputs, target = data 
        # 迁移到GPU，注意迁移的device要和模型的device在同一块显卡
        inputs, target = inputs.to(device), target.to(device)
        # 2.前向传递
        outputs = model(inputs)
        loss = criterion(outputs, target)
        # 3.反向传播
        optimizer.zero_grad()
        loss.backward()
        # 4.更新参数
        optimizer.step()
        
        running_loss += loss.item()
        if batch_idx % 300 == 299:
            print('[%d, %5d] loss:%.3f'%
                  (epoch + 1,
                   batch_idx + 1,
                   running_loss / 300))
            running_loss = 0.0
            

def test():
    correct = 0
    total = 0
    with torch.no_grad():
        for data in test_loader:
            images, labels = data
            images, labels = images.to(device), labels.to(device)
            outputs = model(images)
            # 求出每一行(样本)的最大值的下标,dim = 1即行的维度
            # 返回最大值和最大值所在的下标
            _, predicted = torch.max(outputs.data, dim = 1)
            # label矩阵为N × 1
            total += labels.size(0)
            correct += (predicted == labels).sum().item()
        print('accuracy on test set :%d %% ' % (100 * correct / total))
        return correct / total


if __name__ == '__main__':
    epoch_list = []
    acc_list = []
    
    for epoch in range(10):
        train(epoch)
        acc = test()
        epoch_list.append(epoch)
        acc_list.append(acc)
        
    plt.plot(epoch_list, acc_list)
    plt.ylabel('accuracy')
    plt.xlabel('epoch')
    plt.show()

[1,   300] loss:0.675
[1,   600] loss:0.180
[1,   900] loss:0.131
accuracy on test set :96 % 
[2,   300] loss:0.103
[2,   600] loss:0.093
[2,   900] loss:0.082
accuracy on test set :97 % 
[3,   300] loss:0.075
[3,   600] loss:0.070
[3,   900] loss:0.069
accuracy on test set :98 % 
[4,   300] loss:0.058
[4,   600] loss:0.059
[4,   900] loss:0.061
accuracy on test set :98 % 
[5,   300] loss:0.050
[5,   600] loss:0.055
[5,   900] loss:0.051
accuracy on test set :98 % 
[6,   300] loss:0.048
[6,   600] loss:0.050
[6,   900] loss:0.043
accuracy on test set :98 % 
[7,   300] loss:0.038
[7,   600] loss:0.042
[7,   900] loss:0.047
accuracy on test set :98 % 
[8,   300] loss:0.038
[8,   600] loss:0.039
[8,   900] loss:0.041
accuracy on test set :98 % 
[9,   300] loss:0.039
[9,   600] loss:0.035
[9,   900] loss:0.037
accuracy on test set :98 % 
[10,   300] loss:0.035
[10,   600] loss:0.035
[10,   900] loss:0.034
accuracy on test set :98 %