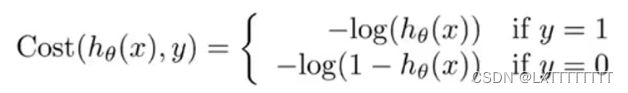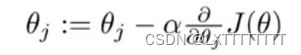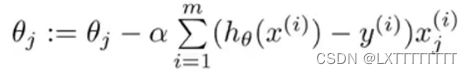机器学习002---Logistic回归

目录

问题的引入

Sigmoid函数(Logistic函数)

梯度下降(Gradient Decent)

正则化(Regularization)

多元分类(Mult-class Classification)

总结

---

问题的引入

        上文(线性回归)中我们讲到线性回归对于离散点的拟合较好，但是对于二分类任务，其y的取值非0(Negative)即1(Positive)，线性回归并不能合理地对数据进行描述。

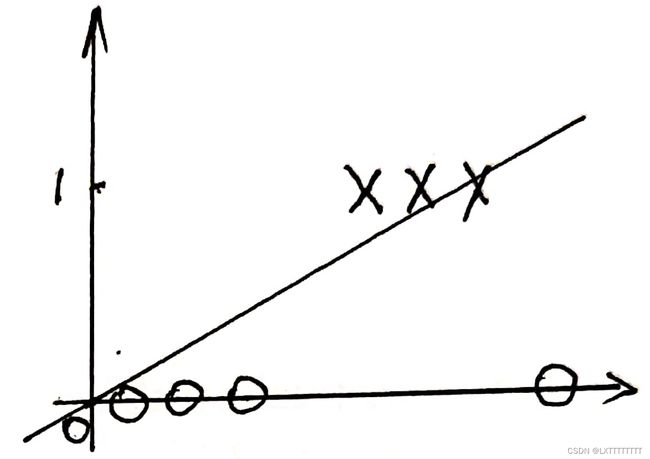线性回归描述二分类任务 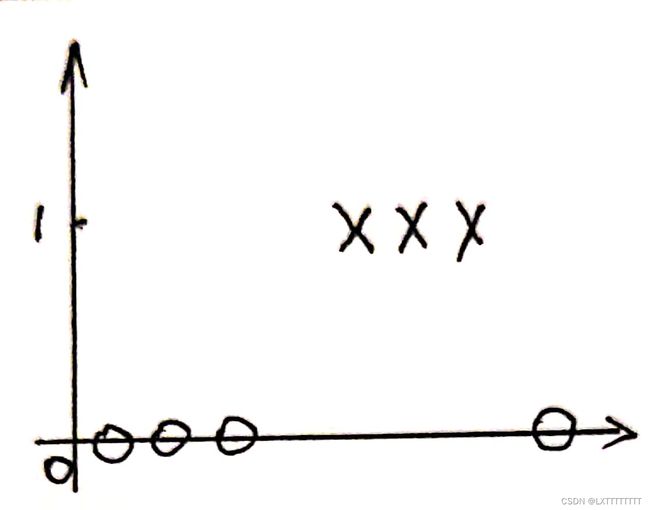二分类任务

、

Sigmoid函数(Logistic函数)

       对于上述问题，我们引入Sigmoid函数(Logistic函数)来描述此类问题。

       Sigmoid函数表达式及图像如下：

 

        注意：Sigmoid函数的值表示在对应的x取值情况下，y为1(Positive)的概率，此项与线性回归不同。同样的，与X代表n + 1维向量，也就是说

          下为Octave/Matlab描述：

function g = sigmoid(z)

g = zeros(size(z));
g = 1 ./ (1 + exp(-z));

end

梯度下降(Gradient Decent)

        同样的当我们使用Logistic回归来解决问题时同样需要描述代价函数，其定义与线性回归相似

(线性回归代价函数详见此文) ，但是由于此二者定义的差距以及二分类任务的特性，对于Logistic回归的代价函数定义如下：

        由于y取值的二元性，可简化如下：       

          下为Octave/Matlab描述：

function [J, grad] = costFunction(theta, X, y)

m = length(y);
J = 0;
grad = zeros(size(theta));

X_ori = X;
X = sigmoid(X * theta);

J = (y' * log(X) + (ones(size(y)) - y)' * log(ones(size(X)) - X)) / (-m);
grad = (X_ori' * (X - y)) / m;

end

        所以同样有梯度下降法来降低代价函数：

        其中为步长。

        注意：此处下降时对所有维度的要同时下降，否则会影响下降结果。 

        对偏导数求值化简得：

        将所得代回Sigmoid函数表达式中所得即为y = 1(Positive)的概率。

        此处采用函数fminunc进行梯度下降，下为Octave/Matlab描述： 

options = optimset('GradObj', 'on', 'MaxIter', 400);

[theta, cost] = fminunc(@(t)(costFunction(t, X, y)), initial_theta, options);

正则化(Regularization)

        正则化是为了避免过拟合的问题，为了解决这个问题我们对代价函数进行部分修正，在原函数的结尾加上惩罚项，公式如下：

         可以看出，公式的前半部分就是之前所提到的公式，后面加上的则是惩罚项，为惩罚的强度，若过小则会出现惩罚不足的情况，所以通常设为1。

        同样的，我们对梯度下降法进行同样的修正：

         下为Octave/Matlab描述： 

function [J, grad] = costFunctionReg(theta, X, y, lambda)

m = length(y);

J = 0;
grad = zeros(size(theta));

X_ori = X;
X = sigmoid(X * theta);
theta1 = [0;theta(2:end)]; 

J = (-1) / m * sum(y .* log(X) + (1 - y) .* log(1 - X)) + lambda / (2 * m) * theta1' * theta1;

grad = 1 / m * X_ori' * (X - y) + lambda / m * theta1;

end

正则化前 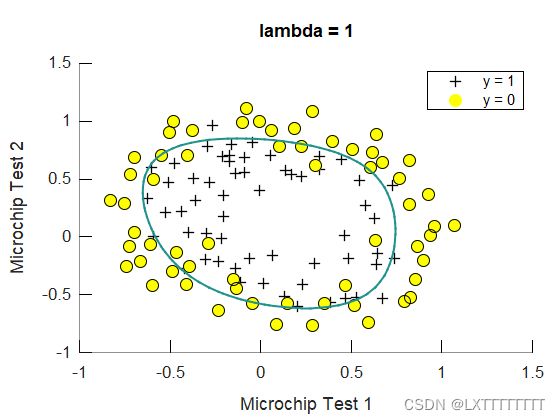正则化后

 

 

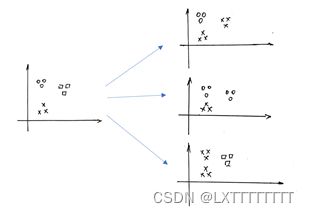
多元分类(Mult-class Classification)

        当数据集y的取值不只0/1两种，而是有n情况时，我们将其分为n个二分类问题，如图：

        计算每个二分类情况的，同时要记住每个抽象出来的二分类问题中0/1所对应的是多元分类中的哪种情况。

        在预测时，对每个x取值都应该有n种代表不同情况的值，取最高的。此时，该所对应的多元分类中情况即是多元分类问题Logistic回归的预测值。

总结

        Logistic回归所用的思想与线性回归大致相似，只是将线性回归中的线性函数替换为了Logistic函数，较为易于理解，对于二分类问题有较好的处理效果。