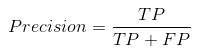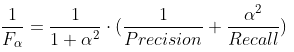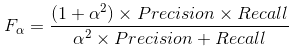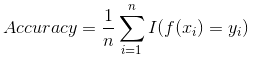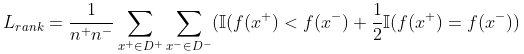【机器学习】分类指标 完全解读
目录
一、评估指标
1.1 分类指标
1.1.1 Precision、Recall、Accuracy、ErrorRate 与 PR
1.1.2 TruePositiveRate、FalsePositiveRate、ROC 与 AUC
1.1.3 Logloss
一、评估指标
评估指标用于反映模型效果。在预测问题中,要评估模型效果,就要将模型预测值 ![]() 与样本的真实值
与样本的真实值 ![]() (Ground-Truth / Label) 进行比较,而评估指标 / 评价得分 (Evaluation Score) 即为
(Ground-Truth / Label) 进行比较,而评估指标 / 评价得分 (Evaluation Score) 即为 ![]() 和
和 ![]() 的函数:
的函数:
![]()
通常,线下使用机器学习评估指标,线上使用业务指标。若线下指标和线上指标不同,则可能出现线下指标变好而线上指标变差的现象 (线下线上不一致)。为此,在一个新问题的开始阶段,都会进行多轮模型迭代,来 探索和线上业务指标一致的线下指标,尽可能使线下指标的变化趋势和线上指标一致。
1.1 分类指标
1.1.1 Precision、Recall、Accuracy、ErrorRate 与 PR
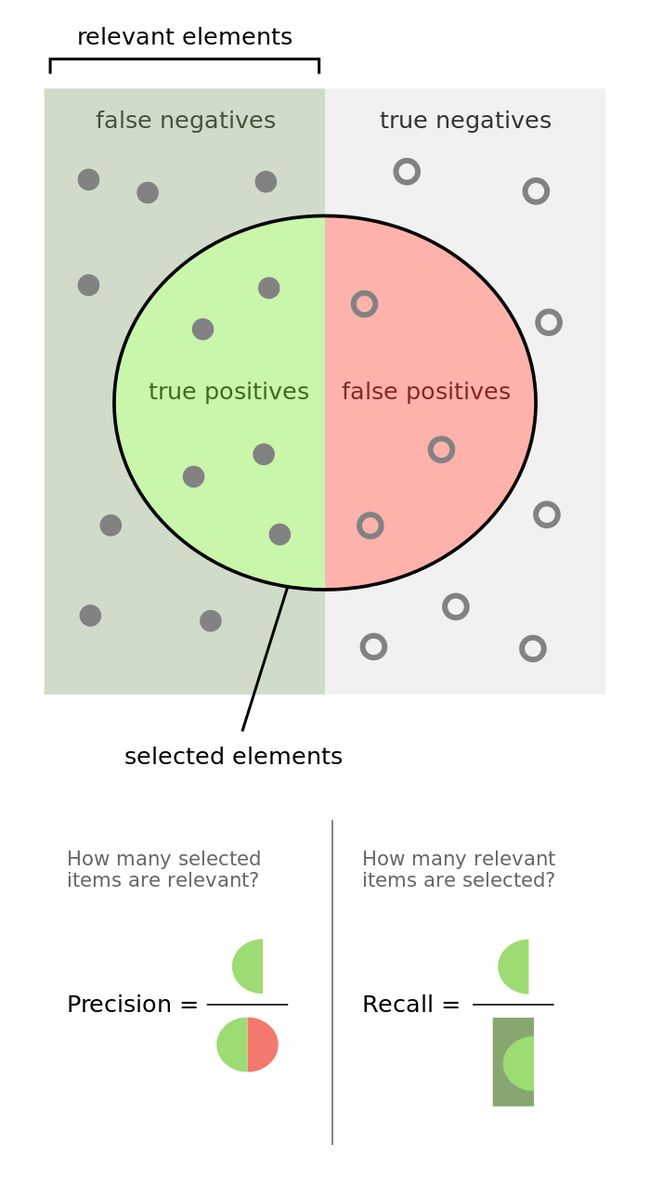
精确率和召回率主要用于 二分类 问题。结合 混淆矩阵 (confusion matrix) 如下所示:
其中,各标识含义为 (注:以下 “正样本”、“正例”、“正类” 等混用):
- TP (真正,True Positive):把 正样本 (P) 正确地 分类为 正类 (P)。换言之,预测的正样本确为 真 的 正 样本
- TN (真负,True Negative):把 负样本 (N) 正确地 分类为 负类 (T)。换言之,预测的负样本确为 真 的 负 样本
- FP (假正,False Positive):把 负样本 (N) 错误地 分类为 正类 (P)。换言之,预测的正样本惜为 假 的 正 样本 —— 实际是 负 样本 (I 类错误)
- FN (假负,False Negative):把 正样本(P) 错误地 分类为 负类 (T)。换言之,预测的负样本惜为 假 的 负 样本 —— 实际是 正 样本 (II 类错误)
可见,样本总数 = TP + TN + FP + FN。
现在,不妨以医院检测为例,设阴性样本 (正常) 为正例 (P),阳性样本 (有疾) 为负例 (N)。TP 和 TN 表示检测试剂准确,将阴性样本正确检测为阴性 (TP),将阳性样本正确检测为阴性 (TP);FP 和 FN 则说明检测试剂有误,把病人检测为正常人 (FP),把正常人检测成病人 (FN)。显然,在医疗检测的场景当中,假阳 (FN) 尚可以接受,假阴 (FP) 则绝对不允许。因为假阳 (FN) 还可以再检测,以确认是真阳 (TN) 还是假阳 (FN);但如果是假阴 (FP),则不但会放过真正的病例 (N),还可能对他人造成危害。因此,医疗检测试剂会比一般标准更加敏感,以提高 ![]() ,避免出现漏网之鱼。
,避免出现漏网之鱼。
- 精确率 / 查准率 (Precision, P):分类正确的正样本数 (TP) 占 预测为正样本的总样本数 (TP + FP) 的比例,其定义为:
可见, ![]() 反映了 所有分类器判断为正例的样本 (TP + FP) 中,真的正样本 (TP) 所占的比例。
反映了 所有分类器判断为正例的样本 (TP + FP) 中,真的正样本 (TP) 所占的比例。
- 召回率 / 查全率 (Recall, R):分类正确的正样本数 (TP) 占 实际的正样本总数 (TP + FN) 的比例,其定义为:
可见, ![]() 反映了 所有实际的正样本 (TP + FN) 中,真的正样本 (TP) 所占的比例。
反映了 所有实际的正样本 (TP + FN) 中,真的正样本 (TP) 所占的比例。
理想时,![]() 和
和 ![]() 二者都越高越好。然而,二者实际是一对 矛盾 的度量:
二者都越高越好。然而,二者实际是一对 矛盾 的度量:![]() 高时,
高时,![]() 低;
低;![]() 低时,
低时,![]() 高。一个原因是 样本存在误差,尤其是临界边缘的数据由于存在误差,导致互相渗透;另一个原因是 模型拟合能力有限,非线性模型以超平面划分样本,若扩大召回,可能导致混入更多错误样本,若提升精度,必然召回会下降。例如,若某模型很贪婪,想要预测尽可能多的样本,那么犯错的概率就会随样本数增加而提升,此时会得到更高的
高。一个原因是 样本存在误差,尤其是临界边缘的数据由于存在误差,导致互相渗透;另一个原因是 模型拟合能力有限,非线性模型以超平面划分样本,若扩大召回,可能导致混入更多错误样本,若提升精度,必然召回会下降。例如,若某模型很贪婪,想要预测尽可能多的样本,那么犯错的概率就会随样本数增加而提升,此时会得到更高的 ![]() 和较低的
和较低的 ![]() ;相反,若某模型很保守,会尽量在 “更有把握” 时才把样本预测为正样本,但会因过于保守而漏掉很多 “没有把握” 的正样本,导致 Recall 值降低,此时会得到更高的
;相反,若某模型很保守,会尽量在 “更有把握” 时才把样本预测为正样本,但会因过于保守而漏掉很多 “没有把握” 的正样本,导致 Recall 值降低,此时会得到更高的 ![]() 和较低的
和较低的 ![]() 。通常,只有某些简单任务才会二者都高。因此,在不同场合需根据实际需求判断哪个指标更紧要,以便于 trade-off。
。通常,只有某些简单任务才会二者都高。因此,在不同场合需根据实际需求判断哪个指标更紧要,以便于 trade-off。
在很多情形下,可根据学习器/模型的预测结果对样例进行排序:排在前面的是学习器/模型认为 “最有可能” 是正例的样本,排在最后的则是学习器/模型认为 “最不可能” 是正例的样本。按此顺序逐个把样本作为正例进行预测。这样,二分类过程就相当于在此排序中以某个 “截断点 (cut point)” 或 “阈值 (threshold)” 将样本分为两份,前半部分判作正例,后半部分判作反例。此时,可计算出各截断点位置上的 ![]() 和
和 ![]() 。若更重视
。若更重视 ![]() ,则设截断点 靠前;若更重视
,则设截断点 靠前;若更重视 ![]() ,则设截断点 靠后。
,则设截断点 靠后。
例如,在排序问题 (Ranking) 中,通常没有一个确定的分类阈值把预测结果直接判定为正样本或负样本,而是采用 Top-N 返回结果的 ![]() 和
和 ![]() 来衡量排序模型的性能。换言之,以 N 为截断点位置/长度或者说分类阈值,则认为模型返回的 Top-N 的结果就是模型判定的正样本,然后分别计算前 N 个位置上的
来衡量排序模型的性能。换言之,以 N 为截断点位置/长度或者说分类阈值,则认为模型返回的 Top-N 的结果就是模型判定的正样本,然后分别计算前 N 个位置上的 ![]() 和
和 ![]() 。然而,为综合评估一个排序模型的好坏,不仅要看模型在不同 Top-N 下的
。然而,为综合评估一个排序模型的好坏,不仅要看模型在不同 Top-N 下的 ![]() 和
和 ![]() ,而且最好绘制出模型的
,而且最好绘制出模型的 ![]() 曲线。
曲线。
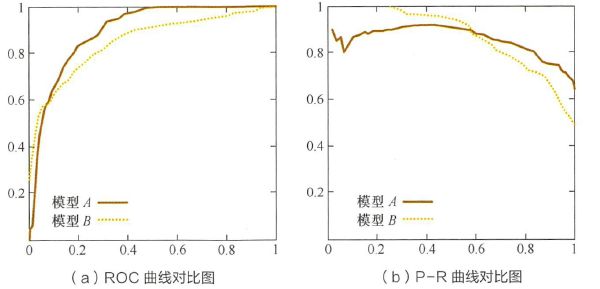
事实上,以 ![]() 为横轴、
为横轴、![]() 为纵轴,描点连线作图,就可以得到 Precision-Recall 曲线 (P-R 曲线),例如:
为纵轴,描点连线作图,就可以得到 Precision-Recall 曲线 (P-R 曲线),例如:
![]()
对于排序模型而言,其 ![]() 曲线上的一个点代表着在某一阈值 N 下,模型将大于该阈值的结果判定为正样本、小于该阈值的结果判定为负样本,此时返回结果对应的
曲线上的一个点代表着在某一阈值 N 下,模型将大于该阈值的结果判定为正样本、小于该阈值的结果判定为负样本,此时返回结果对应的![]() 和
和 ![]() 。整条
。整条 ![]() 曲线是通过将阈值 N 依次从高到调到低而生成的。
曲线是通过将阈值 N 依次从高到调到低而生成的。
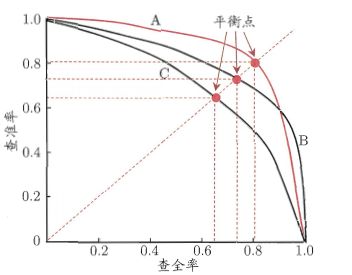
由图上可见,原点附近代表当阈值 N 最大时 (对判定为正例的预测值得分要求最高) 模型的 ![]() 和
和 ![]() 。此时,
。此时,![]() 接近于 0,各模型的
接近于 0,各模型的 ![]() 最高。
最高。![]() 的例子 (如模型 A、B、C) 说明,模型预测值得分排前几位的样本全是真的正样本 (TP) 而没有 “夹杂/混入” 任何假的/错误预测的正样本 (FP = 0);而
的例子 (如模型 A、B、C) 说明,模型预测值得分排前几位的样本全是真的正样本 (TP) 而没有 “夹杂/混入” 任何假的/错误预测的正样本 (FP = 0);而 ![]() 接近 1 但不为 1 的例子 (如算法 1) 表明,即使是预测值得分最高的前几个样本,也包含了错误预测为正样本的情况 (FP ≠ 0)。并且,随着
接近 1 但不为 1 的例子 (如算法 1) 表明,即使是预测值得分最高的前几个样本,也包含了错误预测为正样本的情况 (FP ≠ 0)。并且,随着 ![]() 的增加,
的增加,![]() 整体呈下降趋势。但是,当
整体呈下降趋势。但是,当 ![]() 时,模型 B 的
时,模型 B 的 ![]() 反而超过了模型 A。这充分说明,只用某个点对应的
反而超过了模型 A。这充分说明,只用某个点对应的 ![]() 和
和 ![]() 无法全面地衡量模型的性能,只有通过
无法全面地衡量模型的性能,只有通过 ![]() 曲线整体的表现,才能更全面地评估模型。
曲线整体的表现,才能更全面地评估模型。
比较性能时,若一个模型的 ![]() 曲线被另一者 完全 “包住/覆盖”,则可断言后者优于前者,如模型 A 和 模型 B 总是优于模型 C;若
曲线被另一者 完全 “包住/覆盖”,则可断言后者优于前者,如模型 A 和 模型 B 总是优于模型 C;若 ![]() 曲线 交叉,则难以一般性断言孰优孰劣,只能在具体的
曲线 交叉,则难以一般性断言孰优孰劣,只能在具体的 ![]() 或
或 ![]() 条件下比较,模型 A 和 模型 B 无法肯定地断言孰优孰劣。
条件下比较,模型 A 和 模型 B 无法肯定地断言孰优孰劣。
一方面,可比较 ![]() 与
与 ![]() 的 折中 (trade off) —— 平衡点 (Break-Event Point, BEP),它是
的 折中 (trade off) —— 平衡点 (Break-Event Point, BEP),它是 ![]() 时的取值,如上图红点所示。可见,
时的取值,如上图红点所示。可见,![]() 曲线越靠近右上角的平衡点,则学习器/模型性能越好。
曲线越靠近右上角的平衡点,则学习器/模型性能越好。
另一方面,可比较 ![]() 曲线下的面积大小 —— AP 分数 (Average Precision Score, APS),它在一定程度上表征了学习器/模型在
曲线下的面积大小 —— AP 分数 (Average Precision Score, APS),它在一定程度上表征了学习器/模型在 ![]() 和
和 ![]() 上取得相对 “双高” 的比例。但该值不便计算。为此,存在多种综合考虑
上取得相对 “双高” 的比例。但该值不便计算。为此,存在多种综合考虑 ![]() 与
与 ![]() 的指标/度量,例如:
的指标/度量,例如:
- F1 值 (F1-score):
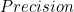 和
和 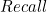 的 调和平均值 (harmonic mean),其定义为 (两种表示):
的 调和平均值 (harmonic mean),其定义为 (两种表示):
![]()
在一些应用中,对 ![]() 和
和 ![]() 的重视程度有所不同。例如,在推荐系统中,目标为尽可能少打扰用户时,更希望推荐内容确是用户感兴趣的,此时
的重视程度有所不同。例如,在推荐系统中,目标为尽可能少打扰用户时,更希望推荐内容确是用户感兴趣的,此时 ![]() 更重要 (精准推荐,宁缺毋滥);而在检验检疫时,为尽可能少漏掉有疫病的样本,更希望找出尽可能多的有嫌疑样本,此时
更重要 (精准推荐,宁缺毋滥);而在检验检疫时,为尽可能少漏掉有疫病的样本,更希望找出尽可能多的有嫌疑样本,此时 ![]() 更重要 (宁可抓错一千,不可放过一个)。
更重要 (宁可抓错一千,不可放过一个)。
- F 值 (F-score):
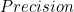 和
和 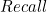 的 加权调和平均 (weighted harmonic mean),其定义为 (两种表示):
的 加权调和平均 (weighted harmonic mean),其定义为 (两种表示):
在 ![]() 的一般泛化形式
的一般泛化形式 ![]() 中,
中,![]() 度量了
度量了 ![]() 对
对 ![]() 的相对重要性,相当于 赋予不同权重以表达出对二者的不同偏好。
的相对重要性,相当于 赋予不同权重以表达出对二者的不同偏好。![]() 时退化为标准
时退化为标准 ![]() ;
;![]() 时
时 ![]() 相对影响更大;
相对影响更大;![]() 时
时 ![]() 相对影响更大。
相对影响更大。
注意,与算术平均 ![]() 和几何平均
和几何平均 ![]() 相比,调和平均更重视较小值。为权衡不同类型错误所造成的不同损失,可为错误赋予 “非均等代价 (unequal cost)”。在非均等代价下,我们所希望的不再是简单地最小化错误次数,而是希望最小化 “总体代价 (total cost)” 。
相比,调和平均更重视较小值。为权衡不同类型错误所造成的不同损失,可为错误赋予 “非均等代价 (unequal cost)”。在非均等代价下,我们所希望的不再是简单地最小化错误次数,而是希望最小化 “总体代价 (total cost)” 。
对于 多分类, F1-score 的两种常用计算方式为 Micro 和 Macro,其中:
- Micro 和二分类计算方式类似,先计算各类别的 TP、FP、FN、TN 并 求和 构成新的 TP、FP、FN、TN,再计算
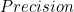 和
和 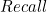 得到 Micro-F1。换言之,统计出各类别的混淆矩阵 并 “相加” 得到一个多类别的混淆矩阵,再计算 F1-score。
得到 Micro-F1。换言之,统计出各类别的混淆矩阵 并 “相加” 得到一个多类别的混淆矩阵,再计算 F1-score。 - Macro 则先计算出各类别的 TP、FP、FN、TN,再分别计算各类别的
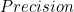 和
和 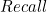 得到各类别的 F1-score,然后再取 算术平均 (各类别权重均等) 得到 Macro-F1。
得到各类别的 F1-score,然后再取 算术平均 (各类别权重均等) 得到 Macro-F1。
可见,二者的区别源于组合先后顺序的差异,但 实际中 Macro 更常用。
在 sklearn 中,F1-score 计算的 API —— fl_score 方法的形参 'average' 是 多类别/多标签 目标函数所必须的,其可选参数包括 None, 'binary' (default), 'micro', 'macro', 'samples', 'weighted',其中:
- None:返回各类别的 F1-score
- binary:仅适用于二分类,当 pos_label 为 1 时,返回类别 1 的 F1-score
- micro:通过先计算总体的 TP、FN 和 FP 的数量,再全局计算 F1-score
- macro:宏 F1,分别计算每个类别的 F1-score,然后取算术平均 (各类别权重均等) —— 视各类别重要性一致 (对占少数类的样本影响较大)
- weighted:作为取算术平均的 macro 算法的改良版,weighted 算法取加权平均 (各类别权重取决于该类样本在总样本数中的占比)
- samples:计算每个实例的度量,并找到它们的平均值
关于更详细的内容,可见:
- fl_score:https://scikit-learn.org/stable/modules/generated/sklearn.metrics.f1_score.html?highlight=f1#sklearn.metrics.f1_score
- Matrics and Scoring:https://scikit-learn.org/stable/modules/model_evaluation.html#precision-recall-f-measure-metrics
此外,更多常用的评估指标:
- 准确率 (Accuracy):分类正确的总样本数 (TP + TN) 占 总样本数 (TP + TN + FP + FN) 的比例,其定义为:
此外,相比于总为 二分类 指标的 ![]() ,
,![]() 能从二分类推广和应用到 多分类,即:
能从二分类推广和应用到 多分类,即:
其实,![]() 是分类问题中最简单和直观的评价指标,但 缺陷 也很明显。比如,当负样本占 99% 时,若分类器把所有样本都预测为负样本 (TN) 也可以获得 99% 的
是分类问题中最简单和直观的评价指标,但 缺陷 也很明显。比如,当负样本占 99% 时,若分类器把所有样本都预测为负样本 (TN) 也可以获得 99% 的 ![]() 。所以,当不同类别的样本比例非常不均衡时,占比大的类别往往成为影响准确率的最主要因素。 为此,可使用更为有效的
。所以,当不同类别的样本比例非常不均衡时,占比大的类别往往成为影响准确率的最主要因素。 为此,可使用更为有效的 ![]() (每个类别下的样本
(每个类别下的样本 ![]() 的算术平均) 作为模型评估的指标。
的算术平均) 作为模型评估的指标。
- 错误率 (Error Rate):分类错误的总样本数 (FP + FN) 占 总样本数 (TP + TN + FP + FN) 的比例,其定义为:
1.1.2 TruePositiveRate、FalsePositiveRate、ROC 与 AUC
很多学习器/模型输出的是预测概率值,而使用 ![]() 和
和 ![]() 这类指标评估模型时,还需对预测概率值设 分类阈值 (threshold)。这使得学习器/模型多了一个 超参数,且此超参数会影响模型的泛化能力。比如,对预测概率值从大到小正序排序,预测概率值大于阈值的前半部分视为正样本,反之视为负样本 —— 相当于前述的 截断点 (cut point) —— 若更重视
这类指标评估模型时,还需对预测概率值设 分类阈值 (threshold)。这使得学习器/模型多了一个 超参数,且此超参数会影响模型的泛化能力。比如,对预测概率值从大到小正序排序,预测概率值大于阈值的前半部分视为正样本,反之视为负样本 —— 相当于前述的 截断点 (cut point) —— 若更重视 ![]() ,则设截断点靠前;若更重视
,则设截断点靠前;若更重视 ![]() ,则设截断点靠后。因此,排序本身的质量好坏,体现了综合考虑学习器/模型 “在不同任务下的期望泛化性能” 的好坏,或者说 “在一般情况下” 泛化性能的好坏。
,则设截断点靠后。因此,排序本身的质量好坏,体现了综合考虑学习器/模型 “在不同任务下的期望泛化性能” 的好坏,或者说 “在一般情况下” 泛化性能的好坏。![]() 曲线正是从这个角度出发来研究学习器/模型泛化性能的有力工具。
曲线正是从这个角度出发来研究学习器/模型泛化性能的有力工具。
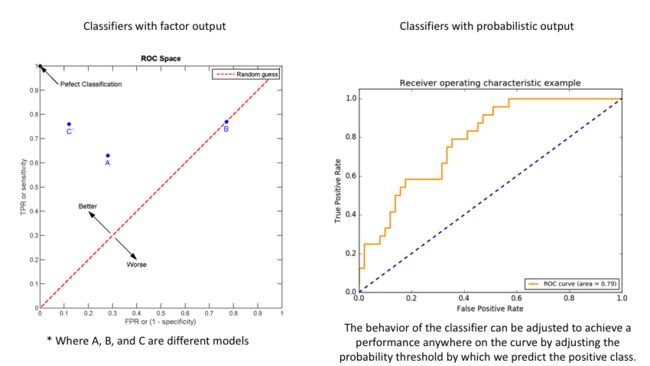
接受者操作特征 / 受试者工作特征 (Receiver Operating Characteristic, ROC) 曲线与 ![]() 曲线类似,根据预测结果对所有样本排序,按此顺序逐个把样本作为正例进行预测 (换言之,以每条样本的预测概率作为分类阈值 / 正负样本分割点)。但区别在于,每次分割后,要计算的是
曲线类似,根据预测结果对所有样本排序,按此顺序逐个把样本作为正例进行预测 (换言之,以每条样本的预测概率作为分类阈值 / 正负样本分割点)。但区别在于,每次分割后,要计算的是 ![]() 和
和 ![]() ,并分别以它们为 横、纵坐标 描点连线作
,并分别以它们为 横、纵坐标 描点连线作 ![]() 曲线图。如下所示:
曲线图。如下所示:
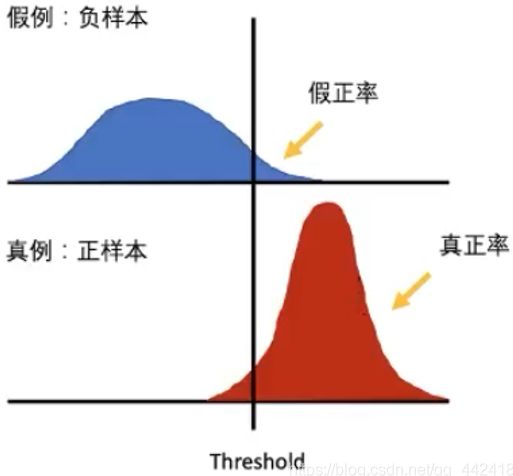
- 真正率 (True Positive Rate, TPR):预测正确的正样本数 (TP) 占 实际的正样本总数 (TP + FN) 的比例,其定义为:
- 假正率 (False Positive Rate, FPR):预测错误的正样本数 (FP) 占 实际的负样本总数 (FP + TN) 的比例,其定义为:
![]() 与
与 ![]() 示意图:
示意图:
![]()
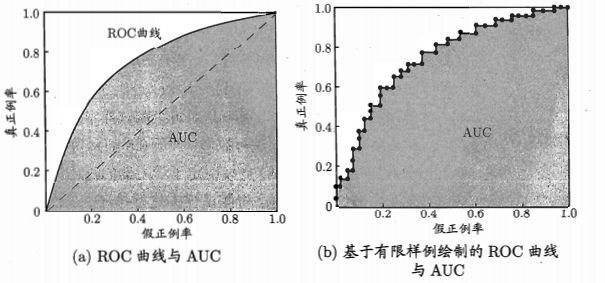
对于 ![]() 曲线图的 各点含义:点 (0, 0) 相当于 根据学习器/模型预测结果对所有样本排序,然后把分类阈值设为最大 (把所有样本均预测为反例,此时,总样本数 = TN + FN,TP = FP = 0),此时
曲线图的 各点含义:点 (0, 0) 相当于 根据学习器/模型预测结果对所有样本排序,然后把分类阈值设为最大 (把所有样本均预测为反例,此时,总样本数 = TN + FN,TP = FP = 0),此时 ![]() 且
且 ![]() 。若进一步 放宽阈值,可以提升
。若进一步 放宽阈值,可以提升 ![]() 和
和 ![]() ,但与此同时
,但与此同时 ![]() 也会提升,此时
也会提升,此时 ![]() 曲线将 从左下角到右上角方向开始 “延伸” (单调递增)。注意,当样本数较少时,
曲线将 从左下角到右上角方向开始 “延伸” (单调递增)。注意,当样本数较少时,![]() 曲线可能呈 锯齿状;但当样本数足够多后,锯齿会变得 光滑。到了 点 (1, 1) 时,
曲线可能呈 锯齿状;但当样本数足够多后,锯齿会变得 光滑。到了 点 (1, 1) 时,![]() 且
且 ![]() ,表明所有的样本都被不加区分地预测成了正例,此时所有正样本都正确预测为真正例 (FN = 0:没有将任何正样本错误预测为负例),但所有负样本也都相应地被错误预测为正例,即假正例 (TN = 0,没有样本被预测为负例)。此外,对于不属于
,表明所有的样本都被不加区分地预测成了正例,此时所有正样本都正确预测为真正例 (FN = 0:没有将任何正样本错误预测为负例),但所有负样本也都相应地被错误预测为正例,即假正例 (TN = 0,没有样本被预测为负例)。此外,对于不属于 ![]() 曲线的 点 (0, 1) 即
曲线的 点 (0, 1) 即 ![]() 且
且 ![]() ,对应于 将所有正样本都正确预测为真正例 (FN = 0:没有将任何正样本错误预测为负例)、所有负样本都正确预测为真反例 (FP = 0:没有将任何负样本错误预测为正例) 的 “理想模型”。最后,对角线 对应于 “随机猜想模型” (概率五五开的瞎猜),是最差的情况。
,对应于 将所有正样本都正确预测为真正例 (FN = 0:没有将任何正样本错误预测为负例)、所有负样本都正确预测为真反例 (FP = 0:没有将任何负样本错误预测为正例) 的 “理想模型”。最后,对角线 对应于 “随机猜想模型” (概率五五开的瞎猜),是最差的情况。
进行学习器/模型比较时,与 ![]() 曲线类似:若一个学习器/模型的
曲线类似:若一个学习器/模型的 ![]() 曲线被另一者 完全 “包住/覆盖”,则可断言后者优于前者,因为在任意
曲线被另一者 完全 “包住/覆盖”,则可断言后者优于前者,因为在任意 ![]() 下,
下,![]() 越大说明 模型可以在分错同样数量负样本的情况下正确预测更多的正样本,这代表了模型区分正负样本的能力更优。若
越大说明 模型可以在分错同样数量负样本的情况下正确预测更多的正样本,这代表了模型区分正负样本的能力更优。若 ![]() 曲线 交叉,则难以一般性断言孰优孰劣,只能在具体的
曲线 交叉,则难以一般性断言孰优孰劣,只能在具体的 ![]() 或
或 ![]() 条件下比较。
条件下比较。
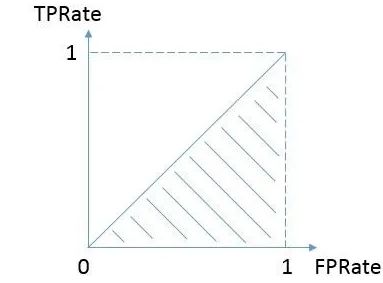
通常,比较 ![]() 曲线下的面积大小 —— AUC (Aera Under ROC Curve),它通过对
曲线下的面积大小 —— AUC (Aera Under ROC Curve),它通过对 ![]() 曲线下各部分面积求和得到。取值越大,说明学习器/模型越可能将正样本排在负样本前面。从物理意义出发,设
曲线下各部分面积求和得到。取值越大,说明学习器/模型越可能将正样本排在负样本前面。从物理意义出发,设 ![]() 曲线是由坐标为
曲线是由坐标为 ![]() 的点 (其实际意义是 (
的点 (其实际意义是 (![]() ,
, ![]() )) 按序连接而形成的
)) 按序连接而形成的 ![]() ,则
,则 ![]() 可按 “直角梯形面积求和公式 (口诀:上底加下底的和乘高除以二)” 估算为:
可按 “直角梯形面积求和公式 (口诀:上底加下底的和乘高除以二)” 估算为:
从概率意义上看,![]() 考虑的是样本预测的排序质量,因此它与排序误差紧密相关。相比于
考虑的是样本预测的排序质量,因此它与排序误差紧密相关。相比于 ![]() 线下面积解释,
线下面积解释,![]() 的排序能力解释为:
的排序能力解释为:![]() 等于随机挑选一个正样本 (P) 和负样本 (N) 时,分类器将正样本排在负样本前面的概率。例如,
等于随机挑选一个正样本 (P) 和负样本 (N) 时,分类器将正样本排在负样本前面的概率。例如,![]() 时,其含义可大致理解为:给定一个正样本和一个负样本,在 60% 的情况下,模型对正样本的打分高于对负样本的打分。可见在该解释下,关心的只有正负样本间的相对分数高低,而具体的分值则无关紧要。注意,
时,其含义可大致理解为:给定一个正样本和一个负样本,在 60% 的情况下,模型对正样本的打分高于对负样本的打分。可见在该解释下,关心的只有正负样本间的相对分数高低,而具体的分值则无关紧要。注意,![]() 最坏的情况是值为 0.5 而非 0,因为若是随机猜测正、负例,那么猜测正确的正例数量将永远占当前猜测数量的 0.5,此时总有
最坏的情况是值为 0.5 而非 0,因为若是随机猜测正、负例,那么猜测正确的正例数量将永远占当前猜测数量的 0.5,此时总有 ![]() ,对应着前面提到的 “随机猜想模型” 的
,对应着前面提到的 “随机猜想模型” 的 ![]() 对角线,如下所示:
对角线,如下所示:
此外,若计算出的 ![]() 小于 0.5,则说明模型可能学习到了样本和特征之间 负相关 的关系,可以试着 调换一下 0 和 1 两个类别,算出来的
小于 0.5,则说明模型可能学习到了样本和特征之间 负相关 的关系,可以试着 调换一下 0 和 1 两个类别,算出来的 ![]() 应该能变成 0.5 以上。
应该能变成 0.5 以上。
更一般地,相比于 ![]() 、
、![]() 等指标,
等指标,![]() 与预测值无关/对预测值不敏感,只关注排序效果/只对排序敏感,因此特别适合 排序业务 (Ranking)。假设采用
与预测值无关/对预测值不敏感,只关注排序效果/只对排序敏感,因此特别适合 排序业务 (Ranking)。假设采用 ![]() 、
、![]() 等指标,而学习器/模型预测的是概率值,就必须选择分类阈值来决定哪些样本预测是正样本 (如 1) 哪些是负样本 (如 0),不同的阈值选择会导致
等指标,而学习器/模型预测的是概率值,就必须选择分类阈值来决定哪些样本预测是正样本 (如 1) 哪些是负样本 (如 0),不同的阈值选择会导致 ![]() 、
、![]() 等指标值不同;而
等指标值不同;而 ![]() 可以直接使用预测概率值本身,参考的是相对顺序,更加好用。结果就是当正、负样本分布发生变化时,
可以直接使用预测概率值本身,参考的是相对顺序,更加好用。结果就是当正、负样本分布发生变化时,![]() 曲线的形状将基本保持不变,而
曲线的形状将基本保持不变,而![]() 曲线的形状通常将发生剧烈的变化。如下图所示,(c) 和 (d) 是将测试集中负样本数量增加 10 倍后的曲线图,可见
曲线的形状通常将发生剧烈的变化。如下图所示,(c) 和 (d) 是将测试集中负样本数量增加 10 倍后的曲线图,可见 ![]() 曲线形状基本不变,这使得
曲线形状基本不变,这使得 ![]() 曲线能够降低不同测试集所带来的干扰,客观衡量模型本身性能,不受正、负样本不均匀的影响。
曲线能够降低不同测试集所带来的干扰,客观衡量模型本身性能,不受正、负样本不均匀的影响。
由于 ![]() 对预测值本身不敏感,常见的正、负样本采样并不会导致
对预测值本身不敏感,常见的正、负样本采样并不会导致 ![]() 的变化。比如在 CTR 预估中,出于计算资源的考虑,有时会对负样本做负采样。由于采样后并不影响正、负样本的顺序分布,
的变化。比如在 CTR 预估中,出于计算资源的考虑,有时会对负样本做负采样。由于采样后并不影响正、负样本的顺序分布,![]() 并不会改变。但若采样并非均匀的,如采用 word2vec 的 negative sampling,其负样本更偏向于从热门样本中采样,则会
并不会改变。但若采样并非均匀的,如采用 word2vec 的 negative sampling,其负样本更偏向于从热门样本中采样,则会 ![]() 将剧烈变化。
将剧烈变化。
此时,给定 ![]() 个正例和
个正例和 ![]() 个负例,令
个负例,令 ![]() 和
和 ![]() 分别表示正、负例集合,则 排序损失 (Ranking Loss) 定义为:
分别表示正、负例集合,则 排序损失 (Ranking Loss) 定义为:
即考虑每一对正、负例,若正例的预测值小于负例,则记一个 “罚分”;若相等,则记 0.5 个 “罚分”。可见,![]() 对应的是
对应的是 ![]() 曲线上分的面积:若一个 正例 在
曲线上分的面积:若一个 正例 在 ![]() 曲线上对应标记点的坐标为
曲线上对应标记点的坐标为 ![]() ,则
,则 ![]() 恰是排序在其之前的负例所占的比例,即
恰是排序在其之前的负例所占的比例,即 ![]() 。从而有:
。从而有:
![]()
此外,关于 ![]() 还有更多的统计意义,如:
还有更多的统计意义,如:![]() 和
和 ![]() 等价;
等价;![]() 与 基尼系数
与 基尼系数 ![]() 满足
满足 ![]() 。
。
其实,关于 ![]() 值本身的意义,在实际业务中,常常会发现点击率模型的
值本身的意义,在实际业务中,常常会发现点击率模型的 ![]() 要低于购买转化率模型的
要低于购买转化率模型的 ![]() 。正如前文所述,
。正如前文所述,![]() 代表模型预估样本间的排序关系,即正、负样本间预测的 gap 越大,
代表模型预估样本间的排序关系,即正、负样本间预测的 gap 越大,![]() 越大。通常,点击行为的成本要低于购买行为,从业务上理解,点击率模型中正、负样本的差别要小于购买力模型,即购买转化模型的正样本通常更容易被预测准。
越大。通常,点击行为的成本要低于购买行为,从业务上理解,点击率模型中正、负样本的差别要小于购买力模型,即购买转化模型的正样本通常更容易被预测准。
![]() 毕竟 是线下离线评估指标,与线上真实业务指标有差别,但差别越小则
毕竟 是线下离线评估指标,与线上真实业务指标有差别,但差别越小则 ![]() 的参考性越高。比如,对于点击率模型和购买转化率模型,虽然购买转化率模型的
的参考性越高。比如,对于点击率模型和购买转化率模型,虽然购买转化率模型的 ![]() 会高于点击率模型,但往往是点击率模型更容易做且线上效果更好。因为,购买决策比点击决策过程长、成本重,且用户购买决策受很多场外因素影响,如预算不够、在别的平台找到更便宜的了、知乎上看了评测觉得不好等,而这部分信息无法收集到,所以最终将导致样本的信息缺失程度高,模型的离线
会高于点击率模型,但往往是点击率模型更容易做且线上效果更好。因为,购买决策比点击决策过程长、成本重,且用户购买决策受很多场外因素影响,如预算不够、在别的平台找到更便宜的了、知乎上看了评测觉得不好等,而这部分信息无法收集到,所以最终将导致样本的信息缺失程度高,模型的离线 ![]() 与线上业务指标差异变大。总之,样本数据包含的信息越接近线上,则离线指标与线上指标 gap 越小。而决策链路越长,信息丢失就越多,则更难做到线下线上一致。好在实际的工作中,常常是模型迭代的
与线上业务指标差异变大。总之,样本数据包含的信息越接近线上,则离线指标与线上指标 gap 越小。而决策链路越长,信息丢失就越多,则更难做到线下线上一致。好在实际的工作中,常常是模型迭代的 ![]() 比较,即新模型比旧模型
比较,即新模型比旧模型 ![]() 高,代表新模型对正、负样本的排序能力优于旧模型。理论上,这个时候上线 AB-test,应该能看到 CTR 之类的线上指标增长。但实际中仍可能发生不一致,首要要做的就是一些低级错误:1) 排除 bug,线上线下模型预测的结果要符合预期;2) 谨防样本穿越,如样本中有时间序列特征,但 train、test 的数据切分未考虑时间因子,则容易造成穿越。
高,代表新模型对正、负样本的排序能力优于旧模型。理论上,这个时候上线 AB-test,应该能看到 CTR 之类的线上指标增长。但实际中仍可能发生不一致,首要要做的就是一些低级错误:1) 排除 bug,线上线下模型预测的结果要符合预期;2) 谨防样本穿越,如样本中有时间序列特征,但 train、test 的数据切分未考虑时间因子,则容易造成穿越。
总而言之,在机器学习的使用场景当中,往往更加看重正例。比如广告的点击率预测、搜索排序、推荐等场景下,更加关注用户点击行为的发生和预测准确情况,而不太关心没有点击是否预测准确。在这些场景中,衡量精确度或者是召回其实不是特别重要,尤其这种涉及排序、摆放位置调整的场景,更加在意模型是否能够把高质量的内容给出一个高的预测分,让它能够排在前面,让用户优先看到,此时 ![]() 往往更能说明模型的能力。因此,相比于
往往更能说明模型的能力。因此,相比于 ![]() ,
,![]() 和
和 ![]() ,在实际的工业应用场景中,可能 使用
,在实际的工业应用场景中,可能 使用 ![]() 更多一些。当然,并非说其他概念不重要,主要还是应用场景决定的。既然应用场景决定了使用
更多一些。当然,并非说其他概念不重要,主要还是应用场景决定的。既然应用场景决定了使用 ![]() 的范围很广,那么当应聘岗位时,问到
的范围很广,那么当应聘岗位时,问到 ![]() 的可能性就很高,尤其是考察候选人基础能力时。如果被问到,光理解
的可能性就很高,尤其是考察候选人基础能力时。如果被问到,光理解 ![]() 是什么意思是不够的,还需要掌握它的应用场景,前因后果,甚至能够进行发散思考一些之前没有想过的问题。
是什么意思是不够的,还需要掌握它的应用场景,前因后果,甚至能够进行发散思考一些之前没有想过的问题。
1.1.3 Logloss
对数损失 (Logistic Loss, logloss) 是对预测概率的 似然估计 (Likelihood Estimation),其标准形式为:
![]()
对数损失最小化本质上是:利用样本中的已知分布,求解导致这种分布的最佳模型参数,使这种分布出现概率最大。
二分类对数损失 :
![]()
其中,![]() 为样本类别标签 (正:1,负:0),
为样本类别标签 (正:1,负:0),![]() 是模型预测第
是模型预测第 ![]() 个样本预测为正类的概率。
个样本预测为正类的概率。
多分类对数损失 :
其中,![]() 为样本总数,
为样本总数,![]() 为类别总数,
为类别总数,![]() 表示第
表示第 ![]() 个样本的类别标签为
个样本的类别标签为 ![]() ,
,![]() 是模型预测第
是模型预测第 ![]() 个样本为类别
个样本为类别 ![]() 的概率。
的概率。
在逻辑回归 (Logistic Regression, LR) 中,损失函数即为对数损失。
而平方损失则很直观,直接度量了真实回归模型与预测回归模型间的差异;而对数损失 则度量了真实条件概率分布与预测条件概率分布间的差异,值越小越好,而这里的差异度量用的是 KL 散度。有别于 ![]() ,
,![]() 对预测概率是敏感的。
对预测概率是敏感的。
参考资料:
《西瓜书》(《机器学习》)
《南瓜书》
《统计学习方法》
《百面机器学习》
《美团机器学习算法实践》
乱弹机器学习评估指标AUC
召回、精确、准确,这些让人头大的概念一文全都讲清楚
你了解如何评估模型吗?
混淆矩阵、AUC、ROC,傻傻分不清楚?来看这篇就对了