王道数据结构笔记01-二叉排序树/二叉查找树/BST

一、二叉排序树的定义

二叉排序树，又称二叉查找树（BST，Binary Search Tree）
一棵二叉树或者是空二叉树，或者是具有如下性质的二叉树：
左子树上所有结点的关键字均小于根节点的关键字；
右子树上所有结点的关键字均大于根节点的关键字。
左子树和右子树又各是一棵二叉排序树。
即：
左子树结点值<根节点值<右子树结点值，默认不允许两个结点的关键字相同。
所以：
进行中序遍历，可以得到一个递增的有序序列；
如下图：

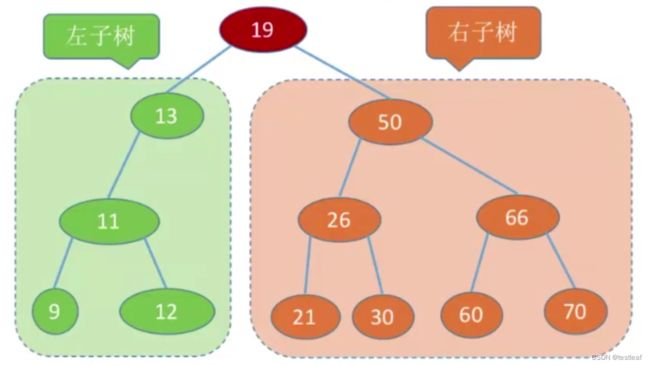
把上图中的右子树提取出来再看，依然满足构成二叉排序树的条件：

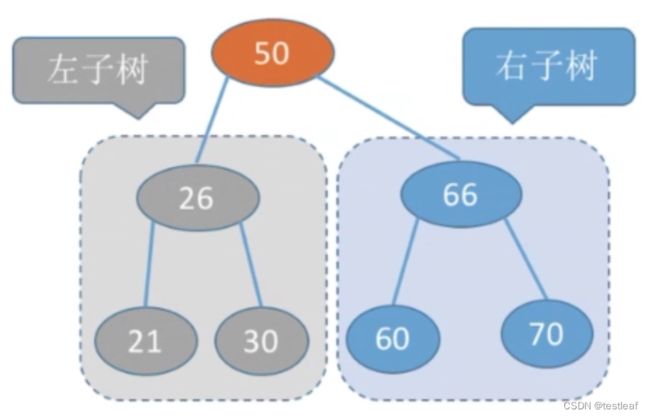
因此：

二叉排序树可用于元素的有序组织、搜索

二叉排序树结点（C语言算法实现）：

typedef struct BSTNode {
	int key;
	struct BSTNode* lchild, * rchild;
}BSTNode, * BSTree;

二、二叉排序树的查找

演示1：查找关键字为9的结点：

若树非空，目标值与根节点的值比较：
若相等，则查找成功；
若小于根节点，则在左子树上查找，否则在右子树上查找。
查找成功，返回结点指针；查找失败，返回NULL；

在二叉排序树中查找值为k的结点（非递归实现）（C/C++算法实现）：
最坏空间复杂度：$O(1)$

BSTNode* BST_Search(BSTree T, int k) {
	while (T != NULL && k != T->key) {	//若树或子树为空，或待查找的值等于根节点值，则结束循环
		if (k < T->key) T = T->lchild;	//小于，则在左子树上查找
		else T = T->rchild;			//大于，则在右子树上查找
	}
	return T;
}

在二叉排序树中查找值为$k$的结点（递归实现）（C/C++算法实现）：
最坏空间复杂度：$O(h)$

BSTNode* BST_Search(BSTree T, int k) {
	if (T == NULL)
		return NULL;	//查找失败
	if (k == T->key)
		return T;		//查找成功
	else if (k < T->key)
		return BST_Search(T->lchild, k);	//在左子树中找
	else
		return BST_Search(T->rchild, k);	//在右子树中找
}

三、二叉排序树的插入

演示2：插入关键字为61的结点：

若原二叉排序树为空，则直接插入结点；
否则，若关键字k小于根节点值，则插入到左子树，
若关键字k大于根节点值，则插入到右子树；

新插入的结点一定是叶子结点

在二叉排序树中插入关键字为$k$的新结点（非递归实现）（C/C++算法实现）：
最坏空间复杂度：$O(1)$

int BST_Insert(BSTree& T, int k) {
	BSTree p = T, parent = NULL;
	char childflag = 0;
	while (p != NULL && k != p->key) {	//若树或子树为空，或待查找的值等于根节点值，则结束循环
		parent = p;
		if (k < p->key) {
			p = p->lchild;		//小于，则在左子树上查找
			childflag = 0;
		}
		else {
			p = p->rchild;		//大于，则在右子树上查找
			childflag = 1;
		}
	}
	if (T == NULL || p == NULL) {
		BSTree t = (BSTree)malloc(sizeof(BSTNode));
		t->key = k;
		t->lchild = t->rchild = NULL;
		if (T == NULL) {			//原树为空，则新插入的结点为根节点
			T = t;
		}
		else if (p == NULL) {
			if (childflag == 0) {
				parent->lchild = t;	//插入到parent的左子树
			}
			else {
				parent->rchild = t;	//插入到parent的右子树
			}
		}
		return 1;				//返回1，插入成功
	}
	else if (k == p->key) {			//树中存在相同关键字的结点，插入失败
		return 0;
	}
}

在二叉排序树中插入关键字为$k$的新结点（递归实现）（C/C++算法实现）：
最坏空间复杂度：$O(h)$

int BST_Insert(BSTree& T, int k) {
	if (T == NULL) {	//原树或子树为空，新插入的结点为根节点
		T = (BSTree)malloc(sizeof(BSTNode));
		T->key = k;
		T->lchild = T->rchild = NULL;
		return 1;	//返回1，插入成功
	}
	else if (k == T->key)	//树中存在相同关键字的结点，插入失败
		return 0;
	else if (k < T->key)	//插入到T的左子树
		return BST_Insert(T->lchild, k);
	else				//插入到T的右子树
		return BST_Insert(T->rchild, k);
}

四、二叉排序树的构造

演示3：按照序列str={57,55,3,94,67,8,4,48,61,75}建立BST：

不同的关键字序列可能得到同款二叉排序树，也可能得到不同款二叉排序树；
如：
str1={50,66,60,26,21,30,70,68}
str2={50,26,21,30,66,60,70,68}
str3={26,21,30,50,60,66,68,70}

按照str[]中的关键字序列建立二叉排序树（C/C++算法实现）：
依次将每个关键字插入到二叉排序树中

void Create_BST(BSTree& T, int str[], int n) {
	T = NULL;	//初始时T为空树
	int i = 0;
	while (i < n) {	//依次将每个关键字插入到二叉排序树中
		BST_Insert(T, str[i]);
		i++;
	}
}

五、二叉排序树的删除

演示4：【情况1-被删除结点是叶节点】删除关键字为32的结点：

演示5：【情况2-被删除结点只有一颗左子树或右子树】删除关键字为29的结点：

演示6：【情况3-被删除结点有左、右两棵子树】删除关键字为65的结点（作为叶子节点的直接后继67进行替代）：

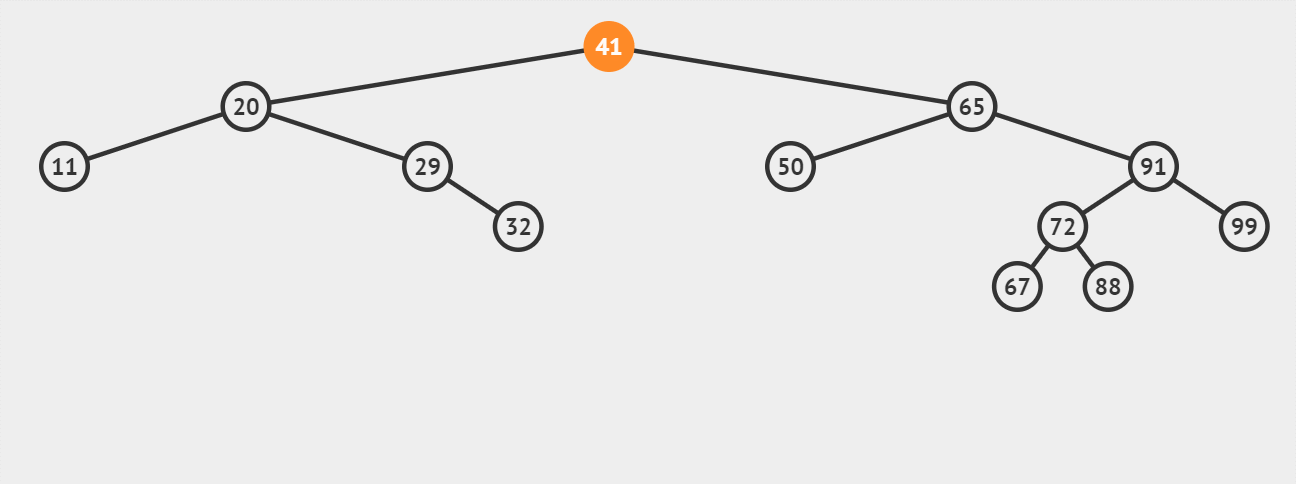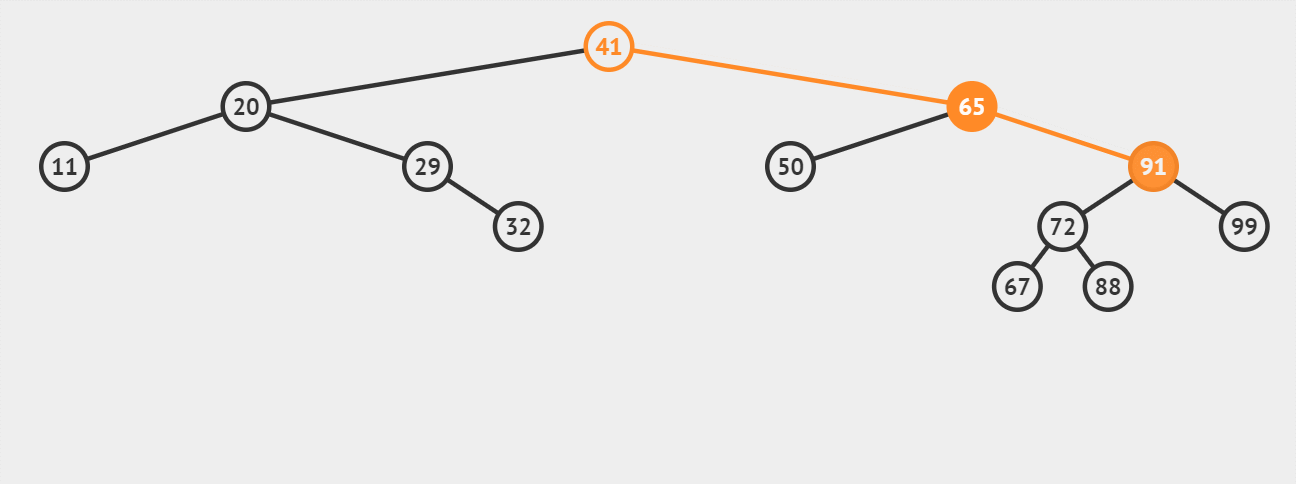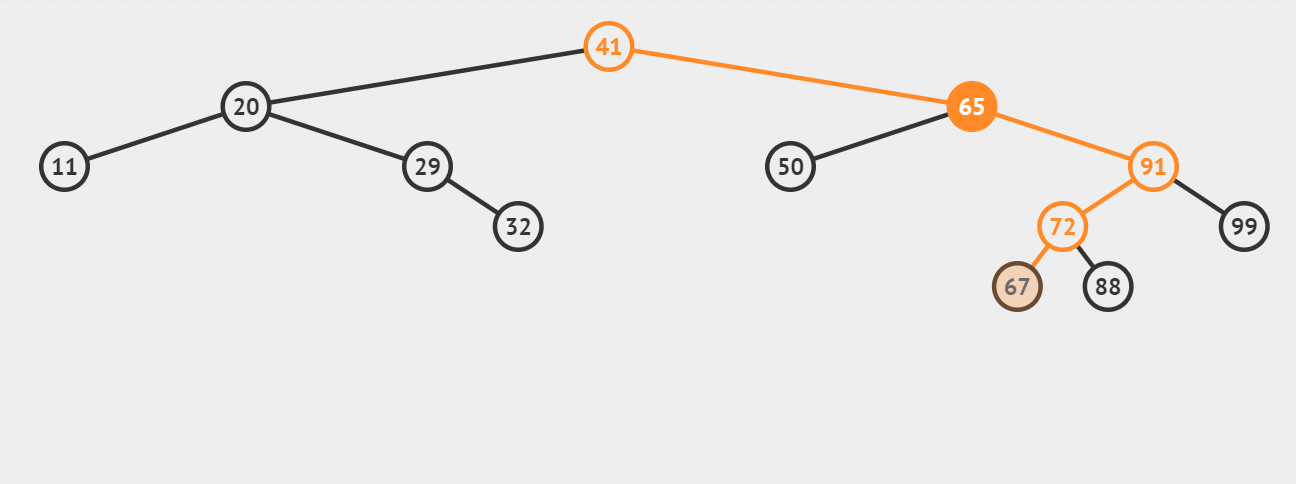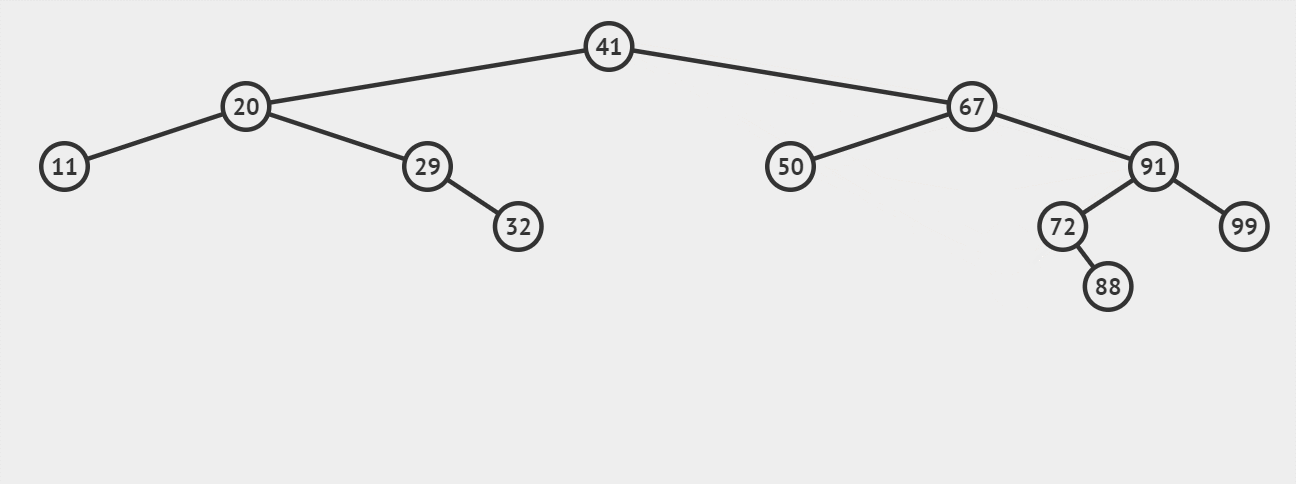
演示7：【情况3-被删除结点有左、右两棵子树】删除关键字为65的结点（不作为叶子节点的直接后继67进行替代）：

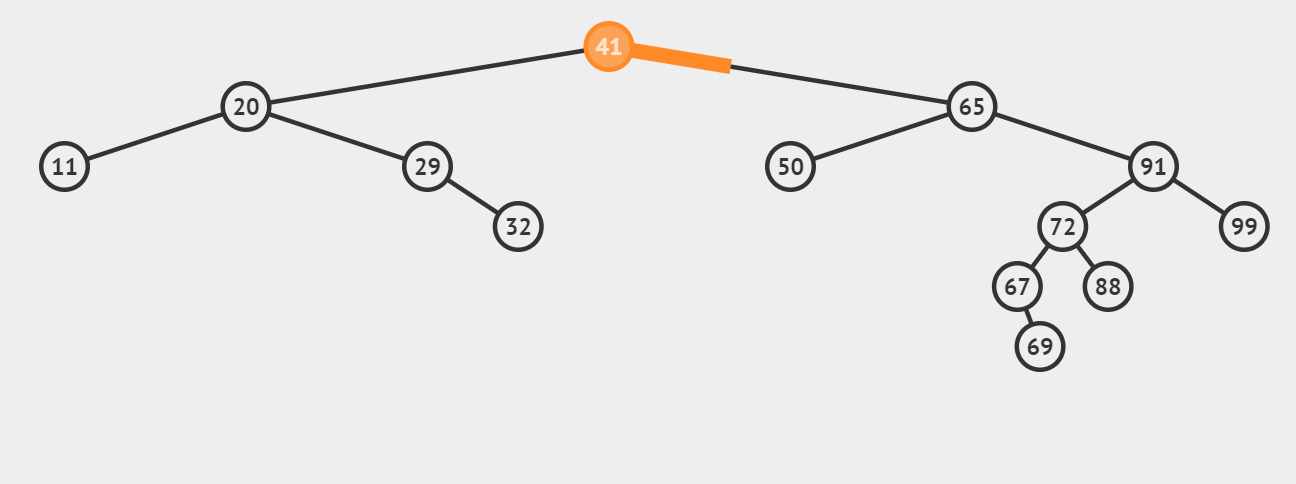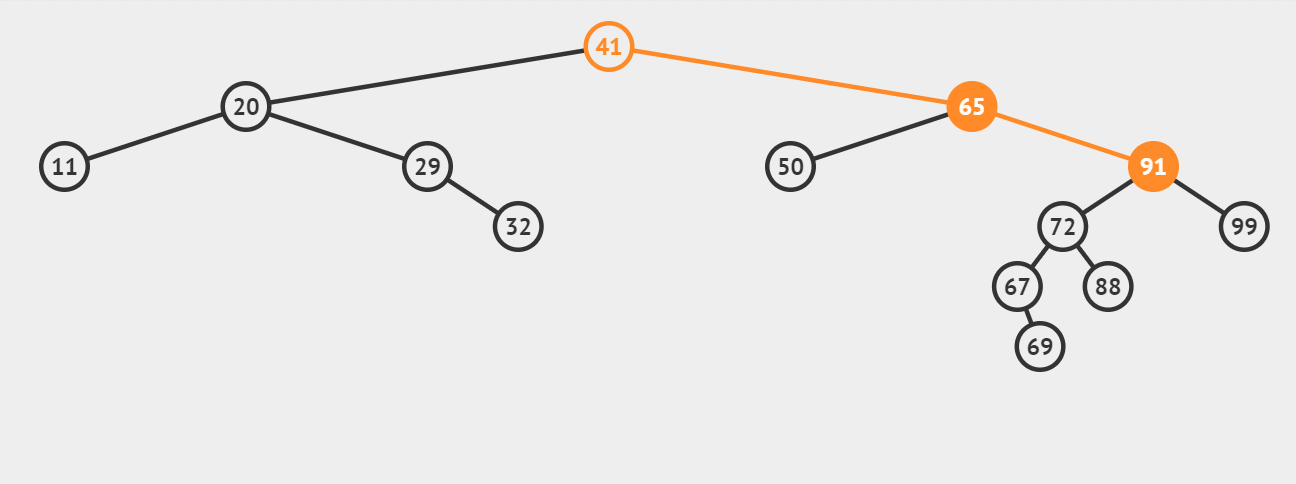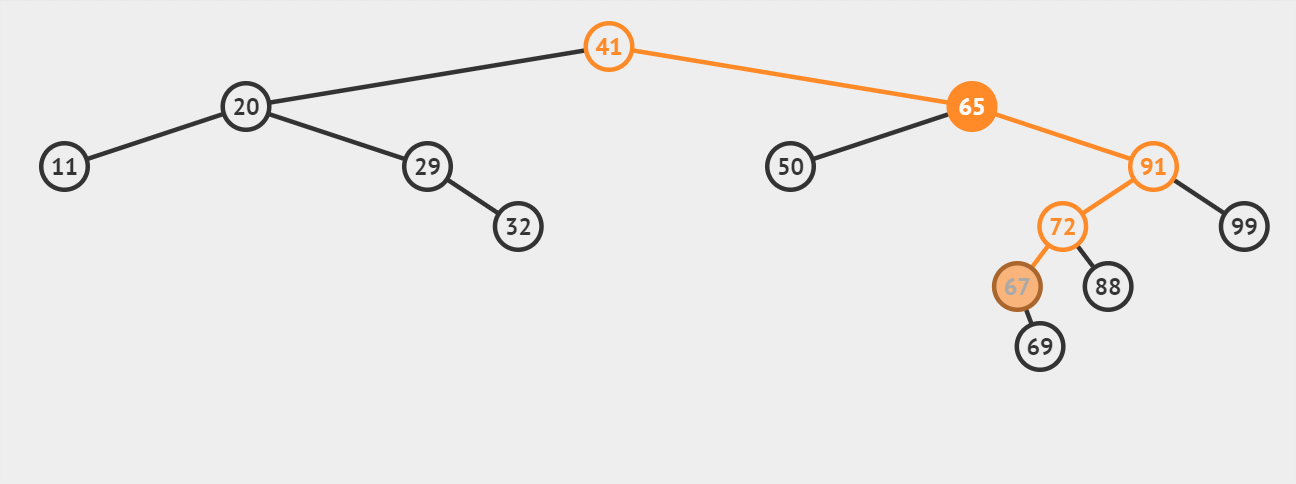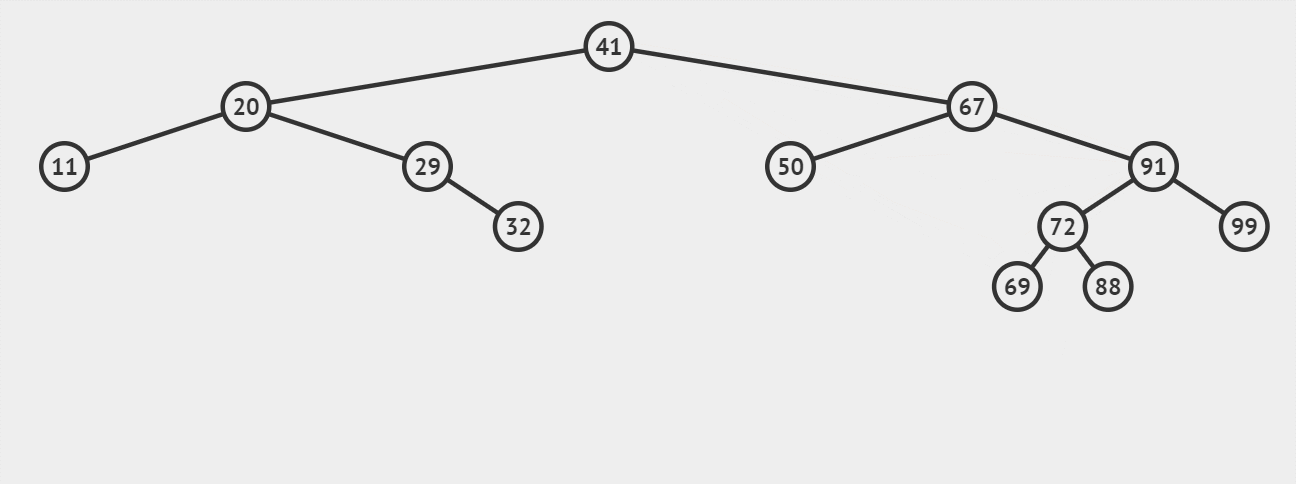
先搜索找到目标结点：
1、若被删除结点z是叶节点，则直接删除，不会破坏二叉排序树的性质（左子树结点值<根节点值<右子树结点值）。
2、若结点z只有一颗左子树或右子树，则让z的子树成为z父节点的子树，替代z的位置。
3、若结点z有左、右两棵子树，则令z的直接后继（或直接前驱）替代z，然后从二叉排序树中删去这个直接后继（或直接前驱），这样就转换成了第一或第二种情况。
注：
由于，二叉排序树的性质：左子树结点值<根节点值<右子树结点值；
所以，对二叉排序树进行中序遍历，可以得到一个递增的有序序列；
z的直接后继：z的右子树中最左下结点（该节点一定没有左子树）；
z的直接前驱：z的左子树中最右下结点（该节点一定没有右子树）；

六、查找效率分析

查找长度：在查找运算中，需要对比关键字的次数称为查找长度，反映了查找操作的时间复杂度。

计算1：查找成功的平均查找长度ASL（Average Search Length）：

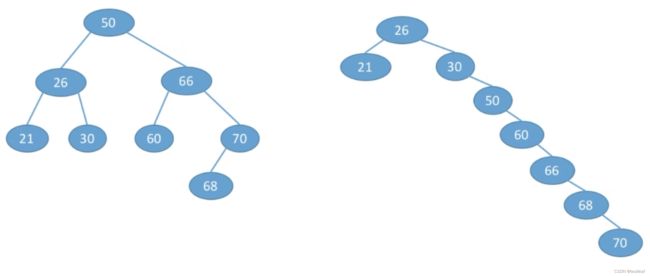
左图：ASL=(1*1+2*2+3*4+4*1)/8=2.625
右图：ASL=(1*1+2*2+3*1+4*1+5*1+6*1+7*1)/8=3.75

若树高$h$，找到最下层的一个结点需要对比$h$次；

最好情况：$n$个结点的二叉树最小高度为$\lfloor lo{g}_{2}n\rfloor +1$，平均查找长度ASL=$O(lo{g}_{2}n)$；
最坏情况：每个结点只有一个分支，树高$h$=结点数$n$。平均查找长度ASL=$O(n)$；

所以，发明了平衡二叉树，树上任一结点的左子树和右子树的深度之差不超过1。

计算2：查找失败的平均查找长度ASL（Average Search Length），需补充失败结点：

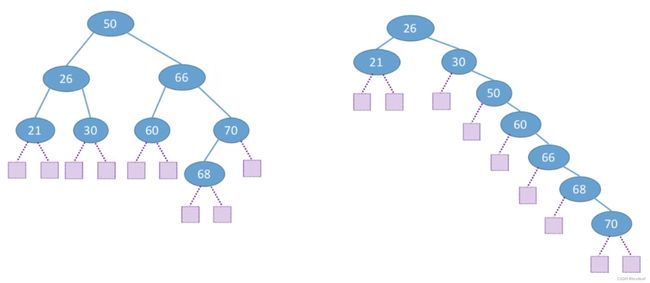
左图：ASL=(3*7+4*2)/9=3.22
右图：ASL=(2*3+3+4+5+6+7*2)/9=4.22

七、C/C++编码实践

为了验证上述C/C++算法代码的准确性，本文采用VS2022进行调试；
1、添加头文件：

#include
#include

2、定义数组大小：

#define MaxSize 50

3、引入二叉树中序遍历的函数：

void visit(BSTree T) {
	printf("%d\t", T->key);
}

void InOrder(BSTree T) {
	if (T != NULL) {
		InOrder(T->lchild);	//递归遍历左子树 
		visit(T);			//访问根节点 
		InOrder(T->rchild);	//递归遍历右子树 
	}
}

4、计算数组实际元素个数的函数：

int getStrCount(int str[]) {
	int i = 0;
	while (str[i] != 0)i++;
	return i;
}

5、把上述二叉排序树的定义、查找、插入、构造算法代码加入，递归和非递归算法选择一种即可；

6、编写main函数进行函数调用并调试：

int main(void)
{
	BSTree tree_p;	//初始化二叉排序树根节点的指针tree_p 
	int tree_str[MaxSize] = { 50,66,66,60,26,21,30,70,68 };	//定义要插入的数据元素数组 
	int tree_count = getStrCount(tree_str);	//获取到数据元素的个数 
	Create_BST(tree_p, tree_str, tree_count);	//创建二叉排序树，将数组里面的数据依次插入并将根节点指针赋值给tree_p  
	InOrder(tree_p);	//根据根节点指针tree_p中序遍历该二叉排序树 
	printf("\n查找元素21，并输出其地址：%p", BST_Search(tree_p, 21));	//调用二叉排序树的查找算法，验证其正确性 
}

免责声明：
1.编写此文是为了更好地学习数据结构，如果损害了有关人的利益，请联系删除；
2.如果文中描述欠妥，请在评论中进行指正；
3.文字编写不易，若感觉有用，点赞收藏关注会让博主很开心哦；
4.此外，本文支持任何形式的转载，转载请注明出处，非常感谢！！！
本文源自：https://blog.csdn.net/testleaf/article/details/125920156
参考：
https://visualgo.net/zh/bst
https://blog.csdn.net/qq_38326829/article/details/122016067
https://blog.csdn.net/qq_30310145/article/details/117333664
https://blog.csdn.net/Peter_tang6/article/details/76832757