CRITIC法之matlab
目录
1.简介
2.原理解析
2.1 指标正向化及标准化
2.2 计算信息承载量
2.3 计算权重和评分
3.实例分析
3.1 读取数据
3.2 指标正向化及标准化
3.3 计算对比度
3.4 矛盾性
3.5 计算信息载量
3.6 计算权重
3.7 计算得分
完整代码
1.简介
CRITIC是Diakoulaki(1995)提出一种评价指标客观赋权方法。该方法在对指标进行权重计算时围绕两个方面进行:对比度和矛盾(冲突)性。
它的基本思路是确定指标的客观权数以两个基本概念为基础。一是对比度,它表示同一指标各个评价方案取值差距的大小,以标准差的形式来表现,即标准化差的大小表明了在同一指标内各方案的取值差距的大小,标准差越大各方案的取值差距越大。二是评价指标之间的冲突性,指标之间的冲突性是以指标之间的相关性为基础,如两个指标之间具有较强的正相关,说明两个指标冲突性较低。
2.原理解析
2.1 指标正向化及标准化
设有m个待评对象,n个评价指标,可以构成数据矩阵X=(xij)m*n,设数据矩阵内元素,经过指标正向化处理过后的元素为xij'
- 若xj为负向指标(越小越优型指标)
![]()
- 若xj为正向指标(越大越优型指标)
![]()
2.2 计算信息承载量
-
对比性
用标准差表示第j 项指标的对比性
![]()
-
矛盾性
矛盾性反映的是不同指标之间的相关程度,若呈现显著正相关性,则矛盾性数值越小。设指标与其余指标矛盾性大小为fj
![]()
rij表示指标i 与指标j 之间的相关系数,在此使用的是皮尔逊相关系数,此为线性相关系数。
-
信息承载量
设指标与信息承载量为Cj
![]()
2.3 计算权重和评分
计算权重:
![]()
信息承载量越大可认为权重越大
计算得分:
![]()
3.实例分析
| 银行 | 资产收益率 | 费用利润率 | 逾期贷款率 | 资产使用 | 自有资本率 |
| 中信 | 0.483 | 13.2682 | 0 | 4.3646 | 5.107 |
| 光大 | 0.4035 | 13.4909 | 39.0131 | 3.6151 | 5.5005 |
| 浦发 | 0.8979 | 25.7776 | 9.0513 | 4.892 | 7.5342 |
| 招商 | 0.5927 | 16.0245 | 13.2935 | 4.4529 | 6.5913 |
3.1 读取数据
data=xlsread('D:\桌面\CRITIC.xlsx')返回:
3.2 指标正向化及标准化
本实例中逾期贷款率为负向指标数据
因此负向指标标准化:
%%负向指标准化处理,
index=[3]; %第三个指标为负向指标
for i=1:length(index)
data1(:,index(i))=(max(data(:,index(i)))-data(:,index(i)))/(max(data(:,index(i)))-min(data(:,index(i))));
end
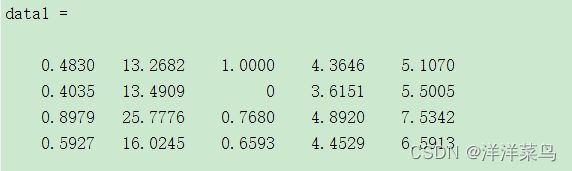
data1返回:
在对剩余数据进行正向指标标准化:
%%正向指标准化处理
index_all=1:size(data1,2);
index_all(index)=[]; % 除负向指标外其余所有指标
index=index_all;
for i=1:length(index)
data1(:,index(i))=(data(:,index(i))-min(data(:,index(i))))/(max(data(:,index(i)))-min(data(:,index(i))));
end
data1返回:
3.3 计算对比度
%%对比性
the=std(data1)返回:
3.4 矛盾性
%%矛盾性
r=corr(data1);%计算指标间的相关系数
f=sum(1-r)返回:
3.5 计算信息载量
%%信息承载量
c=the.*f返回:
3.6 计算权重
%计算权重
w=c/sum(c)返回:
3.7 计算得分
%计算得分
s=data1*w';
Score=100*s/max(s);
yin={'中信','光大','浦发','招商'};
for i=1:length(Score)
fprintf('%s银行百分制评分为:%4.2f\n',yin{1,i},Score(i));
end返回:
完整代码
% CRITIC法分析
clc;clear;
%读取数据
data=xlsread('D:\桌面\CRITIC.xlsx');
%指标正向化和标准化处理后数据为data1
data1=data;
%%负向指标准化处理,
index=[3]; %第三个指标为负向指标
for i=1:length(index)
data1(:,index(i))=(max(data(:,index(i)))-data(:,index(i)))/(max(data(:,index(i)))-min(data(:,index(i))));
end
%%正向指标准化处理
index_all=1:size(data1,2);
index_all(index)=[]; % 除负向指标外其余所有指标
index=index_all;
for i=1:length(index)
data1(:,index(i))=(data(:,index(i))-min(data(:,index(i))))/(max(data(:,index(i)))-min(data(:,index(i))));
end
%%对比性
the=std(data1);
%%矛盾性
r=corr(data1);%计算指标间的相关系数
f=sum(1-r);
%%信息承载量
c=the.*f;
%计算权重
w=c/sum(c);
%计算得分
s=data1*w';
Score=100*s/max(s);
yin={'中信','光大','浦发','招商'};
for i=1:length(Score)
fprintf('%s银行百分制评分为:%4.2f\n',yin{1,i},Score(i));
end