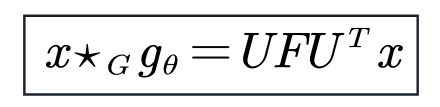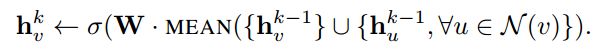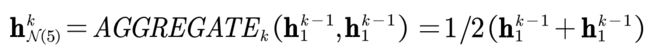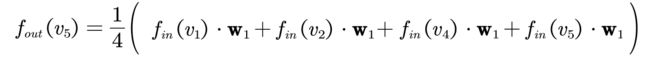【图卷积网络】03-空域卷积介绍 (一)

注：本文为3.1-3.2 空域卷积视频笔记，仅供个人学习使用

---

1、谱域图卷积

1.1 回顾

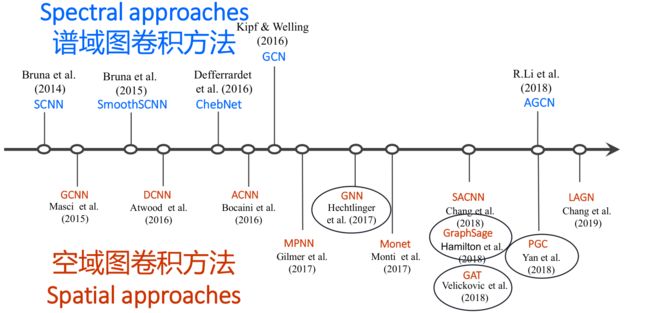
上篇博客【图卷积神经网络】02-谱域图卷积介绍讲到了三个经典的谱域图卷积：

• SCNN用可学习的对角矩阵来代替谱域的卷积核。
  

• ChebNet采用Chebyshev多项式代替谱域的卷积核
  

• GCN可以视为ChebNet的进一步简化。仅考虑1阶切比雪夫多项式，且每个卷积核仅只有一个参数
  
  它们三个的共同特点是：均基于卷积定理和图傅里叶变换。

---

1.2 谱域图卷积的缺陷

1. 谱域图卷积不适用于有向图
   • 图傅里叶变换的应用是有限制的，仅限于在无向图。
   • 谱域图卷积的第一步是要将空域信号转换到谱域，当图傅里叶变换无法使用时，谱域图卷积也就无法进行下去。
   • 在大量的实际场景中，W_ij ≠ W_ji。
2. 谱域图卷积假定固定的图结构
   
   • 模型训练期间，图结构不能变化(不能改变节点之间的权重，不能增删节点)。
   • 在某些场景下，图结构可能会变化（如社交网络数据、交通数据）。
3. 模型复杂度问题
   • SCNN需要进行拉普拉斯矩阵的谱分解，计算耗时，复杂度为 。
   • ChebNet和GCN不需要进行谱分解。但是其可学习的参数过于简化。降低模型复杂度的同时也限制了模型的性能。

---

能否绕开图谱理论，重新定义图上的卷积？本文介绍四种空域图卷积模型，每一个模型可以视为对于上述问题的四个不同的回
答

1. GNN
2. GraphSAGE
3. GAT
4. PGC
   

2、四个空域卷积模型

---

2.1 GNN

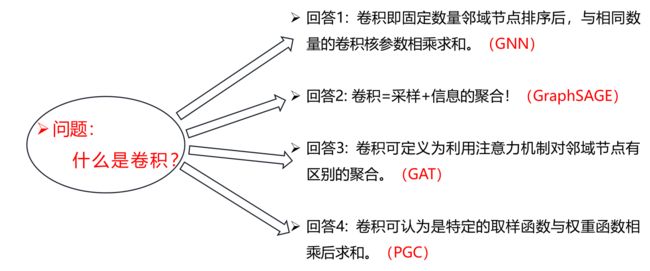
2.1.1 问题：什么是卷积？

论文：GNN Hechtlinger Y, Chakravarti P, Qin J, et al. A Generalization of Convolutional Neural Networks to Graph-Structured Data.[J]. arXiv: Machine Learning, 2017

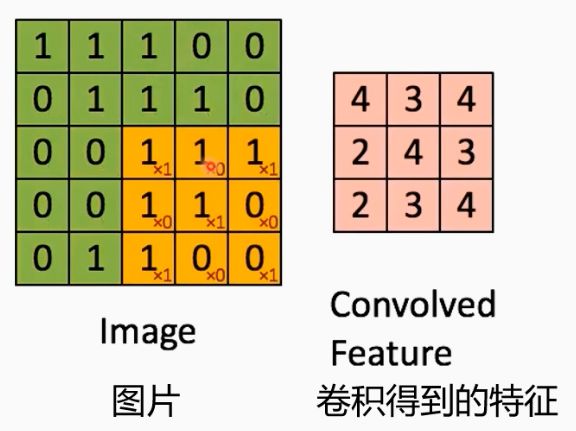
回答1：== 卷积即固定数量邻域节点排序后，与相同数量的卷积核参数相乘求和==。传统卷积的有着固定的邻域大小（如3X3的卷积核即为八邻域），同时有着固定的顺序（一般为左上角到右下角）。

2.1.2 核心思想

卷积的操作可以分为两步

1. 构建邻域。
   • 找到固定数量的邻居节点。
   • 对找到的邻居节点进行排序。
2. 对邻域的点与卷积核参数内积

对于图结构数据而言，构建邻域存在一些困难：

1. 不存在固定八邻域结构。每个节点的邻域大小是变化的。
2. 同一邻域内的节点不存在顺序
   

2.1.3 解决思路

1. 使用==随机游走(random walk)==的方法，根据被选中的概率期望大小选择固定数量的邻居节点。
2. 然后根据节点被选择的概率期望来对邻域进行排序。

符号标记

1. 为图上的随机游走转移矩阵，其中 P_ij 表示由 i 节点到 j 节点的转移概率。

2. 相似度矩阵（similarity matrix）为 S。文中的相似度矩阵可以理解为邻接矩阵W。

3. D 为度矩阵， 。

2.1.4 具体步骤

• GNN假设存在图转移矩阵 。假如图结构是已知的，那么 和 即为已知。随机游走概率转移矩阵定义如下：P = D^-1S。
• 使用归一化的邻接矩阵来作为转移矩阵！
• 多步的转移期望定义为：
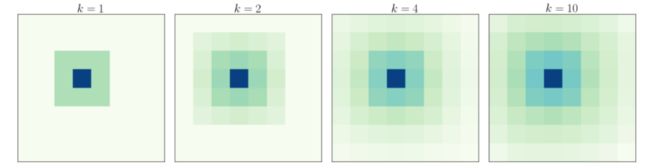
• 根据期望大小来选择邻域，Π_i^(k)表示节点的序号。该节点为（k步内）由i节点出发的访问期望数第c大的节点。那么有：
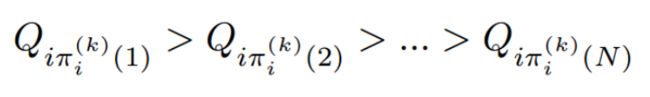
• 执行1D卷积（内积）
  

---

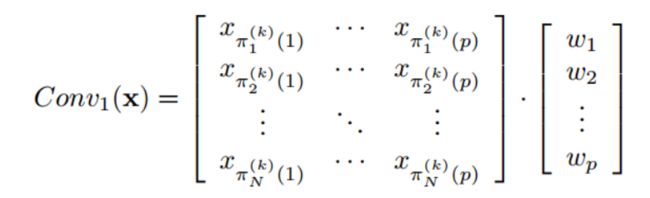
2.1.5 CNN卷积操作示例

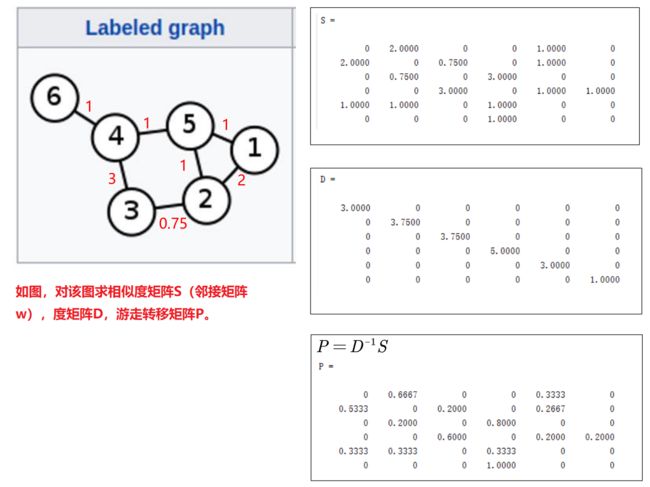
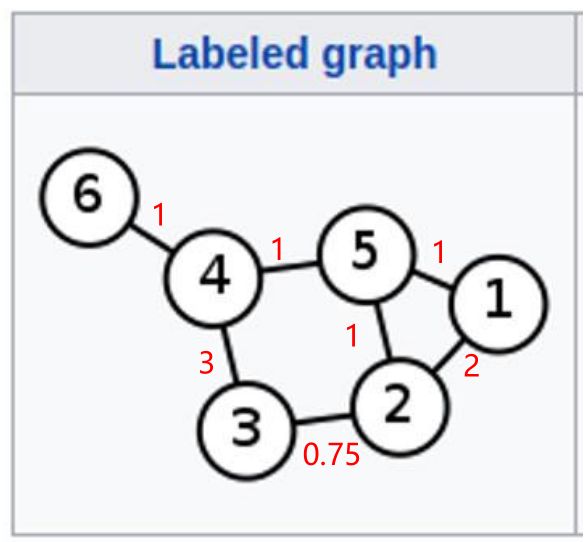
Pⁿ 这个矩阵的元素 Pⁿ_ij 的意义是：从 i 节点出发走 n 步 到 j 节点的概率。实际上是对相似度矩阵S（邻接矩阵D）做了归一化，使得每一行加起来是1，可以表示概率。

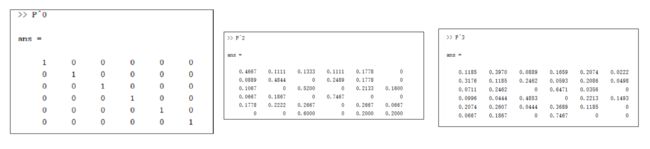
计算期望Q，假设最大走3步，即k=3.
根据Q，选择p个节点作为邻域。假设p=3.

执行1D卷积.对于5号节点而言，其卷积操作如下：
其中 x^c₅ 为第c层 的5号节点上的信号。注意 x₅ ，x₂ ，x₁ 的顺序不能变，是根据期望大小排列的。

---

2.1.6 实验结果

论文：GNN Hechtlinger Y, Chakravarti P, Qin J, et al. A Generalization of Convolutional Neural Networks to Graph-Structured Data.[J]. arXiv: Machine Learning, 2017

分子活性检测和在MNIST数据集上的实验。
这个方法优于传统的全连接层（ Fully connectedNN ）和随机森林（ Random Forest ）。

---

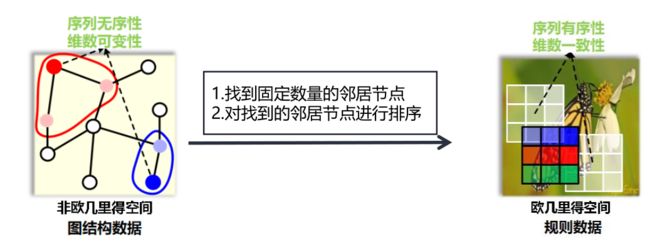
对GNN的再思考：本质上，GNN的做法是强制将一个图结构数据变化为了一个类似规则数据。从而可以被1D卷积所处理。

---

2.2 GraphSAGE

2.2.1 问题：什么是卷积？

论文：Inductive representation learning on large graphs, in Proc. of NIPS, 2017

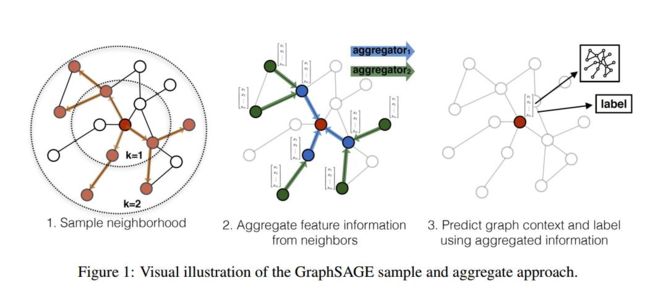
回答2: 卷积=采样+信息的聚合！

2.2.2 核心思想

• 将卷积分为采样和聚合两步。
• SAGE 的简写为： Sample and AggreGatE
• 聚合函数必须与输入顺序无关。 即作者认为邻域的节点不需要进行排序。

2.2.3 实现过程

1. 通过采样，得到邻域节点。
2. 使用聚合函数来聚合邻居节点的信息，获得目标节点的embedding；
3. 利用节点上聚合得到的信息，来预测节点/图的label;
   卷积=采样+信息的聚合！

• 采样
  • GraphSAGE采用均匀采用法(Uniform Sampling)来采样固定的邻域节点。即对于某一节点，在其一阶相连的节点上均匀采样以构建一个固定节点数量的邻域。对同一节结点在不同批次迭代中采样的结点可能是不同的。
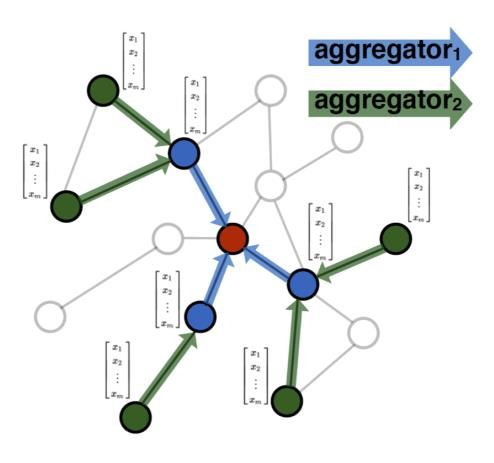
• 聚合

  • Mean aggregator
    

  • LSTM（长短期记忆递归神经网络，是一种特殊的递归神经网络） aggregator。使用LSTM来encode邻居的特征。这里忽略掉邻居之间的顺序，即随机打乱，输入到LSTM中.

• Pooling aggregator.
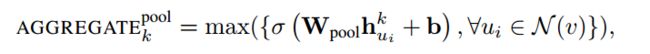
• 前向计算流程

与GNN的不同之处

• 在GNN（以及传统CNN）中需要确定邻域节点的顺序。但是，GraphSAGE的作者认为图卷积邻域的节点不需要进行排序。
• 在GNN中邻域里的每个节点拥有不同的卷积核参数。在GraphSAGE中邻域里的所有节点共享同样的卷积核参数。
• 在邻域选择方法上，GNN通过随机游走的概率大小来构建邻域，GraphSAGE通过均匀采样构建邻域。

---

2.2.4 GraphSAGE卷积操作示例

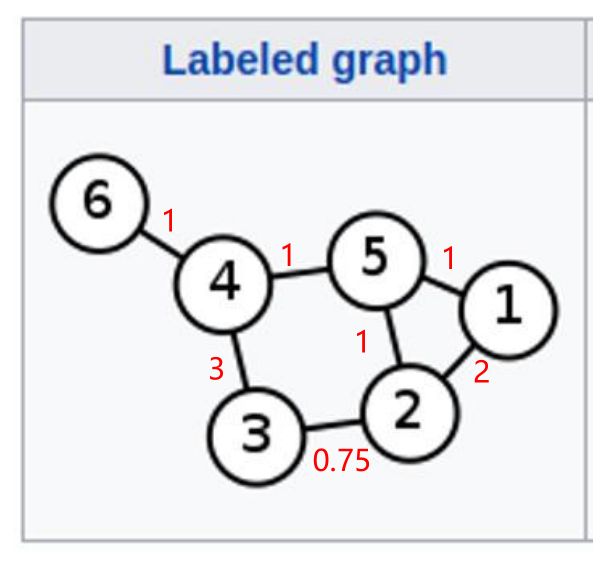
对于5号节点， 有1号、2号、4号三个一阶相邻的节点。这三个节点是候选节点，从这三个节点中采样，来构建5号节点的邻域。

• 假设取均值聚合函数。假设现在正处于第k层。
• 假设需要采样2个节点（有放回的采样）。对5号节点的邻域的的某一次采样的结果为：1号节点和4号节点。
• 在第一步，聚合邻域节点的结果为：
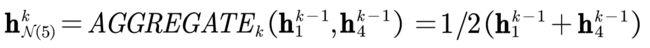
• 在第二步，结合中心节点信息的结果为：
  h^k₅即第k层的输出。

---

在另一次迭代采样时，对5号节点的邻域的的某一次采样的结果为：1号节点和1号节点（由于是有放回的采样，这是有可能的）。

• 在第一步，聚合邻域节点的结果为：
• 第二步是一样的
  
  h^k₅即第k层的输出。

---

2.2.5 实验结果

论文：Inductive representation learning on large graphs, in Proc. of NIPS, 2017

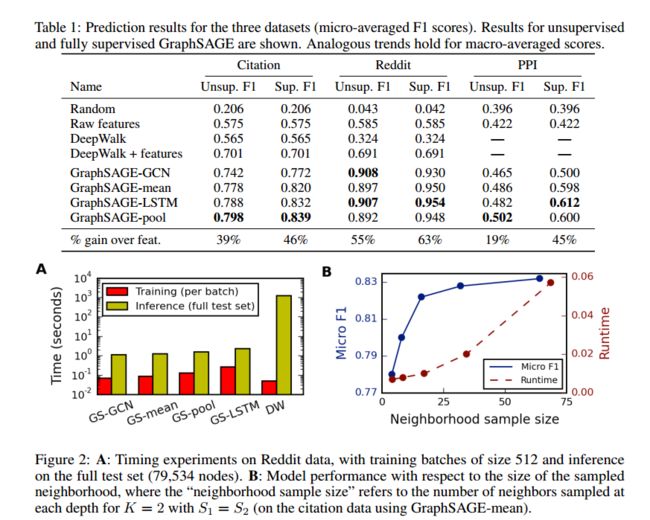
• 效果上 GraphSAGE优于DeepWalk等传统方法。
• 计算时间上， GraphSAGE 中 LSTM 训练速度最慢，但相比DeepWalk， GraphSAGE 预测时间减少 100-500 倍。
• 此外对GraphSAGE而言，（图 B 中表示）随着邻居采样数量递增， F1 增大，计算时间也变大。
• “unsup F1”和“sup F1”分别指在无监督学习和监督学习下的结果。

---

2.3 GAT

2.3.1 问题：什么是卷积？

论文：GRAPH ATTENTION NETWORKS ICLR 2018

回答3: 卷积可定义为利用注意力机制（attention）对邻域节点有区别的聚合。

什么是attention?

注意力机制是一种能让模型对重要信息重点关注并充分学习吸收的技术。它模仿了人类观察物品的方式。核心逻辑就是「从关注全部到关注重点」

2.3.2 核心思想

• GAT即 GRAPH ATTENTION NETWORKS，其核心思想为将attention引入到图卷积模型中。
• 作者认为邻域中所有的节点共享相同卷积核参数会限制模型的能力。因为邻域内的每一个节点和中心节点的关联度都是不同的，在卷积聚合邻域节点信息时需要对邻域中的不同的节点区别对待。
• 利用attention机制来建模邻域节点与中心节点的关联度。

2.3.3 具体步骤

1. 使用注意力机制计算节点之间的关联度

   • 计算关联度
     

   • softmax归一化。为了使不同节点之间的注意力系数易于比较，作者使用softmax函数对每个节点的注意力系数进行归一化。
     

2. 利用注意力系数对邻域节点进行有区别的信息聚合，完成图卷积操作。

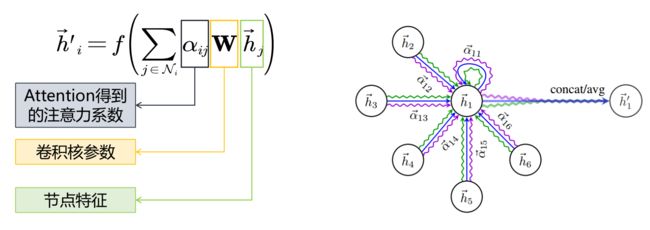
2.3.4 GAT卷积操作示例

1. 对于5号节点， 有1号、2号、4号三个一阶相邻的节点。这三个节点是GAT的邻域。
2. 使用注意力机制计算节点之间的关联度。比如5号节点和1号节点的关联度如下：
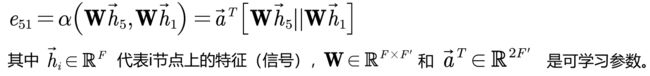
3. softmax归一化
   
4. 利用注意力系数对邻域节点进行有区别的信息聚合，完成图卷积操作。
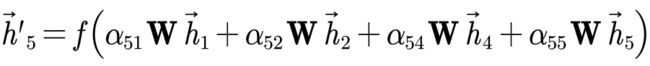
   注意，4个邻域节点的W是通用的。

2.3.5 实验结果

论文：GRAPH ATTENTION NETWORKS ICLR 2018。

2.3.6 与其他图卷积的比较

1. 在邻域节点构建上，不同于GNN（随机游走）、GraphSAGE（采样），GAT直接选用一阶相邻节点作为邻域节点（和GCN类似）。
2. 在节点排序上，GAT中的邻域的所有节点无需排序并且共享卷积核参数（和GraphSAGE类似）。
3. 由于GAT引入了Attention机制，可以构建相邻节点的关系，是对邻域节点的有区别的聚合。若将 α_ij 和 W 结合起来看做一个系数，实际上GAT对邻域的每个节点隐式地（implicitly）分配了不同的卷积核参数。

2.3.7 对GAT的再思考

1. GAT可以认为是对局部图结构的一种学习。现有的图卷积方法常常更关注节点特征(feature) 而忽视了图结构 (structure)。
   
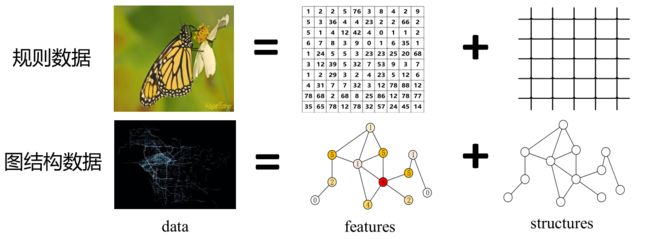
2. Attention机制可认为是一个中带有可学习参数的可学习函数。利用Attention机制，GAT通过构建一个可学习的函数来得到相邻节点之间的关系，即局部图结构。

2.4 PGC

2.4.1 问题：什么是卷积？

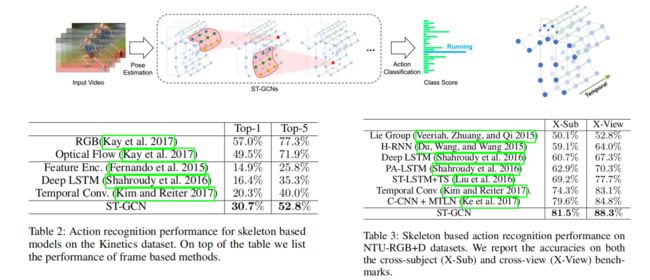
论文：Spatial Temporal Graph Convolutional Networks for Skeleton-Based Action. AAAI. 2018.

回答4: 卷积可认为是特定的取样函数（sample function）与特定的权重函数（weight function）相乘后求和。

从经典卷积出发，K x K 的卷积核可以写成下式：

K是卷积核大小（常见为3） 。P （ ）为一个取样函数. 即在邻域内依次取出节点，来参与卷积计算。w（）为权重函数，对取出来的来的节点分配卷积核参数。 这整个式子实际上就是节点特征与卷积核参数 的内积。

2.4.2 核心思想

将卷积从规则数据扩展到图结构数据的过程中，选择合适的取样函数和权重函数

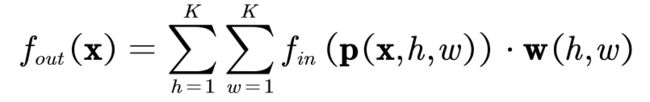
取样函数

• 取样函数即在邻域内依次取出节点。重点在于如何构建节点的邻域，也就是说取样函数在哪里取样。
• 在图结构数据上，PGC可以定义取样函数在D阶近邻的节点上 。即
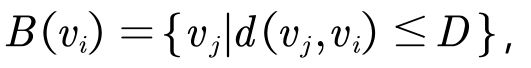
  其中 d(v_j, v_i) 表示从i节点到j节点的最短距离。
• 在实验中取D=1，且在1阶邻域中挨个取样。但是也可以设置成其他的邻域。

权重函数

• 首先将邻域内的点分为K个不同的类。
  
  由于分类操作，因此本方法被称之为Partition Graph Convolution (PGC)。
• 每一类共享一个卷积核参数。不同类之间卷积核参数不同。
  

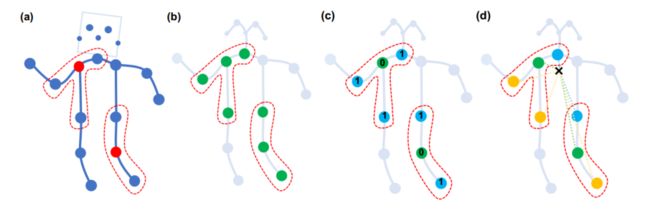
权重函数的分类策略

• Uni-labeling （图b）。邻域里的所有节点一视同仁。只有一个类别。所以全部划分为一个颜色。
• Distance partitioning（图c）。根据阶数不同来确定不同类别。零阶就是自己，是一个类，一阶是另一个类，全部是蓝色。
• Spatial configuration partitioning （图d）、根据与人体骨架中心的距离来分类。有三个类别。距中心距离小于中心结点的为一个类（蓝色），大于的是一类（黄色）。
  

PGC定义在图上的卷积公式最终如下：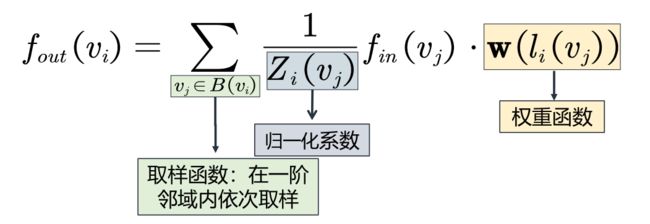
Z_i (v_j) 的意义为（在i节点的邻域中的）j 节点所处类的节点数量。归一化系数是为了平衡邻域中每一类节点的贡献。

2.4.3 PGC卷积操作示例

• 对于5号节点， 有1号、2号、4号三个一阶相邻的节点。这三个节点是PGC的邻域。取样函数依
  次从1号、2号 、4号、5号节点中取样。顺序无所谓，因为每一个节点对应的参数是通过权重函
  数指派的。

• 假设权重函数分类时，将5号节点分为 第1类，1号和2号节点分为第二类，4号节点是第三类。

• 假设权重函数分类时，将四个节点分为一类。

• 假设权重函数分类时，四个节点分为不同的四类，每一个类别一个节点。

2.4.4 实验结果

2.4.5 与其他图卷积的关系

• 相比于GraphSAGE使用均值采样确定邻域，PGC将邻域构建定义为一个取样函数，更加有泛化性。
• GNN需要确定邻域顺序，GraphSAGE邻域的点不需要排序。 PGC采用了更加泛化的做法—定义权重函数。GNN/GraphSAGE的对邻域节点做法可以看做PGC的两个极端—各不相同/一视同仁。

---

3、小结

3.1 空域卷积本质

不同的空域图卷积方法本质上对应着对卷积的不同理解。

3.2 空域图卷积的特点

• 绕开了图谱理论，无需将信号在空域和谱域之间转换。
• 直接在空域上定义卷积操作，更加直观。
• 没有图谱理论的束缚，定义更加灵活，方法更加多样。
• 和谱域图卷积相比，缺少数学理论支撑 。

3.3 四种空域图卷积对比

卷积方法	对卷积定义	邻域节点选择方法	邻域节点是否需要排序	同一邻域内，卷积核参数是否共享
GNN	固定数量邻域节点排序后，与相同数量的卷积核参数相乘求和	随机游走	需要排序	不共享
GraphSAGE	采样+信息的聚合	均匀采样	不需要排序	共享
GAT	利用注意力机制对邻域节点有区别的聚合	直接使用一阶近邻节点	不需要排序	共享。但通过注意力机制修正后每个节点实际上分配到了不同的卷积核参数
PGC	特定的取样函数与特定的权重函数相乘后求和	由特定的取样函数决定	由特定的权重函数决定	由特定的权重函数决定

3.4 对图结构的要求

• GNN、GraphSAGE和GAT不要求固定的图结构，即训练集和测试集的图结构可以不相同。
• PGC文中没有讨论这个问题。他们的实验也均作用于固定结构的图数据。
• 但是作为一个泛化性较强的框架，上述三种卷积都可看做为PGC的特例，可以认为PGC并不要求图结构必须固定。
• 本质上是由于空域图卷积没有使用图傅里叶变换，不需要考虑拉普拉斯矩阵L变化后基函数（拉普拉斯矩阵的特征向量U）改变的问题。