QDROP: RANDOMLY DROPPING QUANTIZATION FOR EXTREMELY LOW-BIT POST-TRAINING QUANTIZATION

QDROP：用于极低比特训练后量化的随机丢弃量化

Xiuying Wei 1, 2 ∗ , Ruihao Gong 1, 2 ∗ , Yuhang Li 2 , Xianglong Liu 1 , Fengwei Yu 2 1 State Key Lab of Software Development Environment, Beihang University, 2 SenseTime Research { weixiuying,gongruihao,liyuhang1 } @sensetime.com,[email protected]

摘要

    最近，训练后量化（PTQ）引起了人们的广泛关注，以产生无需长时间再训练的高效神经网络。尽管成本低，但当前的PTQ工作在极低的位设置下往往会失败。在本研究中，我们率先证实，将激活量化适当纳入PTQ重建有利于最终精度。为了深入理解其内在原因，建立了一个理论框架，表明优化的低位模型在校准和测试数据上的平坦度至关重要。基于这一结论，提出了一种简单而有效的方法，称为QDROP，该方法在PTQ期间随机丢弃激活的量化。在计算机视觉（图像分类、目标检测）和自然语言处理（文本分类和问答）等各种任务上的大量实验证明了其优越性。使用QDROP，首次将PTQ的极限推到2位激活，精度提升可达51.49%。
    QDROP为PTQ建立了一个新的技术水平，没有任何花哨。我们的代码位于https://github.com/wimh966/QDrop并已集成到MQBench（https://github.com/ModelTC/MQBench ).

1引言

    近年来，深度学习已应用于各行各业，为人们的生产和活动提供了极大的便利。在深度神经网络的表现不断提高的同时，内存和计算成本也快速增加，给边缘设备带来了新的挑战。模型压缩技术，如网络剪枝（Han等人，2015）、蒸馏（Hinton等人，2015）、网络量化（Jacob等人，2018）和神经架构搜索（Zoph&Le，2016）等，致力于减少计算和存储开销。在本文中，我们研究了量化，它采用低比特表示权重和激活，以实现定点计算和更少的内存空间。
    根据量化算法的成本，研究人员通常将量化工作分为两类：（1）量化感知训练（QAT）和（2）训练后量化（PTQ）。
    QAT通过利用整个数据集和GPU工作来微调预训练的模型。相反，由于PTQ不需要端到端的训练，因此获得量化模型所需的计算量要少得多。因此，由于PTQ在实践中的低成本和易于使用的特点，近年来，PTQ（Cai等人，2020；Wang等人，2020；Hubara等人，2021；Banner等人，2019；Nahshan等人，2019；Zhang等人，2021a；Li等人，2021c）受到了注意力。
    传统上，PTQ通过执行舍入到最近运算来追求精度，其重点是最小化参数空间中与全精度（FP）模型的距离。在最近的进展中，Nagel等人（2020年）；李等人（2021a）考虑了最小化模型空间中的距离，即最终损失目标。他们使用泰勒展开来分析损耗值的变化，并推导出一种通过学习舍入方案来重构预训练模型特征的方法。
    这种方法在4位量化中是有效的，甚至可以将权重量化的限制推到2位。然而，极低比特激活量化面临更多挑战，仍然无法实现令人满意的精度。我们认为，一个关键原因是现有的理论只将权重量化作为扰动进行模型，而忽略了激活。
    这将导致相同的优化模型，无论激活使用哪一位，这显然违反直觉，从而导致次优解。
    本文首次深入研究了PTQ中激活量化的影响。
    我们经验地观察到，感知激活量化有利于极低比特PTQ重建，并且令人惊讶地发现，只有部分激活量化更可取。
    直观的理解是，合并激活将导致不同的优化权重。
    受此启发，我们对激活量化如何影响权重调整进行了理论研究，得出的结论是，将激活量化纳入重建有助于模型在校准数据上的平坦度，而减少部分量化有助于测试数据上的平坦度。基于经验和理论发现，我们提出了在PTQ重建过程中随机丢弃量化的QDROP，以从一般角度追求平坦度。通过这种简单有效的方法，我们在各种任务上建立了最先进的PTQ，包括图像分类、计算机视觉的目标检测以及自然语言处理的文本分类和问答。
    为此，本文做出以下贡献：1。我们前所未有地证实了在PTQ重建中涉及激活量化的好处，并意外地观察到部分参与激活量化的性能优于整体。
    2.建立了一个理论框架，深入分析了将激活量化纳入权重调整的影响。利用该框架，我们得出结论，校准数据和测试数据上优化的低位模型的平坦度对最终精度至关重要。
    3.在实证和理论分析的基础上，我们提出了一种简单而有效的方法QDROP，从总体上实现了平面度。QDROP易于实现，并且可以作为各种神经网络的即插即用模块，持续增强现有方法，包括诸如ResNets的CNN和诸如BERT的Transformers。
    4、在大量任务和模型上的大量实验证明，我们的方法为PTQ建立了新的技术水平。使用QDROP，2位训练后量化第一次成为可能。

2准备工作

    基本符号。在本文中，矩阵（或张量）标记为X，而向量表示为X。有时我们用w表示权重矩阵w的展平版本。运算符·标记为标量乘法，标记为矩阵或向量的元素乘法。对于矩阵乘法，我们将W x表示为矩阵向量乘法，或将W x表示为矩阵矩阵乘法。
    对于具有激活函数的前馈神经网络，我们将其表示为G（w，x），损失函数表示为L（w，x），其中x和w分别表示网络输入和权重。注意，我们假设x是从训练数据集D t中采样的，因此最终损失由网络正向函数的表示，我们可以将其写成：

，其中W i，j表示连接第j个激活神经元和第i个输出的权重。括号上标（）是层索引。f（·）表示激活功能。
    训练后量化。均匀量化器映射连续值x∈ R转化为不动点整数。例如，激活量化函数可以写成，其中b·e表示舍入到最近的算子，s是两个后续量化级别之间的步长。虽然四舍五入到最近操作使x̂和x之间的均方误差最小化，但参数空间的最小化肯定不能等于最终任务损失的最小化（李等人，2021a），即。然而，在训练后设置中，我们只有一个很小的子集，它只包含1k个图像。因此，在数据有限的情况下，很难最小化最终损失目标。
    最近，一系列工作（Nagel等人，2020；Li等人，2021a）学习向上或向下取整，并将新的取整机制视为权重扰动，即ŵ=w+∆ w以预先训练的网络气体为例，他们利用泰勒展开来分析目标，这揭示了权重之间的量化相互作用：

，其中

是预期的二阶导数。上述目标可以转化为输出黑森加权的输出变化。

。
    关于上述最小化，他们仅通过重构每个块/层输出来微调权重（参见图1中的情况1）。但他们没有研究输出重建期间的激活量化，仅将权重量化建模为噪声。激活量化的步长在重构阶段之后确定。
    直观地说，当将全精度模型的激活量化为2位或3位时，应该有不同的合适权重。然而，由于忽略激活量化，现有工作导致相同的优化权重。因此，我们认为在量化神经网络时，激活量化引起的噪声应与权重一致考虑。

3方法

    在本节中，为了揭示在输出重构之前引入激活量化的影响，我们首先进行了实证实验，并提出了两个观察结果。然后建立了一个理论框架来研究激活量化如何影响优化权重。最后，结合分析结论，提出了一种简单而有效的QD-ROP方法。

图1：优化第k个块的权重舍入时涉及激活量化的3种情况。激活在蓝色块内量化，在橙色块内不量化。

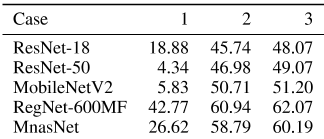
表1:ImageNet数据集在不同情况和不同模型下的2位或3位训练后量化精度。

3.1经验观察

    为了研究重建层/块输出时激活量化的影响，我们在ImageNet（Russakovsky等人，2015）数据集上进行了初步实验。我们的实验基于开源代码李等人（2021a），但我们将引入从1到k的激活量化− 第k个块重建前1个块。我们在图1中给出了一个简单的可视化，显示了将激活量化置于不同阶段的3种情况。情况1意味着在重构块输出期间，所有激活都保持在32位全精度，这也被纳格尔等人（2020）的现有工作所采用；李等人（2021a）。情况2和情况3用于将激活量化合并到重构阶段。然而，情况3将省略当前块的量化，而情况2将不会。表1列出了这三种情况的详细结果（为了在2位上获得崩溃结果，对ResNet-18、ResNet-50和W3A3的2位（W2A2）量化进行了比较）将该算法放在算法2中。
    根据比较，我们可以得到两个观察结果：1。对于极低比特量化（例如W2A2），当在权重调整期间考虑激活量化时，将有巨大的精度提高。通过与案例1和案例2的比较，这一点得到了证实。我们发现情况1几乎不收敛，而情况2达到了良好的精度。这表明，单独优化权重和激活无法找到最优解。
    引入激活量化后，权重将学习减少激活量化的影响。
    2.部分引入分块激活量化优于引入整体激活量化。情况3没有量化当前调谐块内的激活，但实现了比情况2更好的结果。这启发我们，我们为权重调整引入多少激活量化将影响最终精度。

3.2激活量化如何影响权重调整

    经验观察突出了PTQ管道期间激活量化的重要性。为了进一步探索激活量化将如何影响权重调整，我们构建了一个理论框架，在权重和激活都被量化的情况下分析最终损失目标，这为极低比特训练后量化提供了高精度的线索。
    传统上，激活量化可以建模为注入施加在全精度对应物上的某种形式的噪声，定义为e=（â− a）。为了消除激活范围1的影响，我们将噪声转换为乘法形式，即â=a·（1+u），其中u的范围受位宽度和舍入误差的影响。新形式噪声的详细说明见附录A。
    这里，采用1+u（x）表示激活噪声，因为它与特定的输入数据点x有关。有了噪声，我们在计算损耗函数时添加了另一个参数，并在PTQ中定义了我们的优化目标：

我们在此使用一种可以吸收激活时的噪声并转移到权重的变换，其中权重的扰动表示为1+v（x）（v（x）在矩阵乘法格式中使用）。
    考虑一个简单的矩阵向量乘法，通过向前传递，我们得到了由

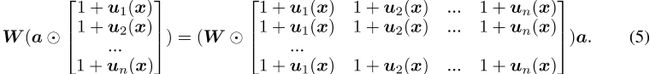
通过取得出的 ，激活向量上的量化噪声可以移植到权重扰动（1+v（x））。注意，对于特定的输入数据点x，有两个不同的。Sec提供证据。B、 1。
    还要注意，对于卷积层，我们不能应用这种变换，因为卷积的输入是一个矩阵，将导致不同的V。尽管如此，我们可以给出一个吸收u（x）并保持相应v（x）的形式引理（严格证明见附录B.2节）：引理1。对于量化（卷积）神经网络，激活量化对训练后量化中最终损失目标的影响可以转化为权重扰动。

。
    通过将插值到引理1中，我们可以得到最终定理：定理1。对于具有量化权重ŵ和激活扰动1+u（x）的神经网络G，我们有：

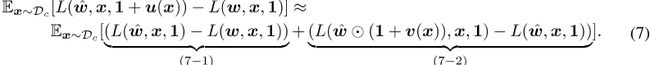
在这里，定理1将优化目标分为两项。项（7-1）与（Nagel等人，2020；Li等人，2021a）中探索的等式（2）相同，揭示了重量量化如何与损失函数相互作用。项（7-2）是通过引入激活量化的额外损耗变化。
    在解释等式（7）的另一种方式中，项（7-2）表示权重量化网络G（ŵ，x）上具有抖动的损耗变化。这种噪声与某些鲁棒性相关。
    正如一些关于泛化和平坦性的著作（Dinh等人，2017；Hochreiter&Schmid-huber，1997）所述，直观地说，平坦最小值意味着在参数扰动下损失变化相对较小，否则，最小值是尖锐的。在本文中，我们遵循（Neyshabur等人，2017）中定义的平坦度概念，该概念从统计期望的角度考虑了损失变化。正如（Neyshabur等人，2017年）和（姜等人，2019年）所述，我们考虑相对于参数幅度的扰动幅度，并将公式视为

，其中vis的每个元素是从噪声分布D和L中采样的随机变量，代表训练集上的优化目标。从这个角度来看，项（7-2）可以解释为具有与输入数据相关的扰动的平面度，因此我们可以实现以下推论。
    推论1。在校准数据x上，在激活量化噪声u（x）的情况下，存在相应的权重摄动v（x），其满足训练的量化模型在摄动v（x）下更平坦。
    第2节讨论了推论1、情况2和3。3.1享受更平坦的损失景观，受益于感知激活量化。这解释了它们与案例1相比的优越性。图2中校准数据（左部分）的锐度测量进一步验证了这一点。在扰动幅值相似的情况下，情况2和3的损耗衰减比情况1小。

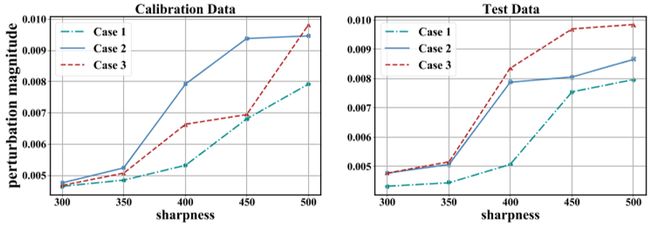
图2：测量三种情况下不同数据分布的锐度。我们采用（Keskar等人，2016）中定义的测量。在损失变化率相同的情况下，那些能够承受较大扰动幅度的人可以享受更平坦的损失景观。

3.3 QDROP

    如上所述，理论证明引入激活量化可以产生比现有工作更平坦的模型，平坦度的方向取决于数据分布。由于PTQ对校准数据特别敏感（Yu等人，2021），我们需要在Sec中传输调查。3.2将校准数据输入测试设置中，以便彻底了解。具体来说，我们在测试集上考虑等式（7），并在下面分别检查两项。基于这些分析，我们将推导出QDROP方法，以在测试数据上追求卓越的表现。
    测试集上的项（7-1）。如第。3.2通过量化激活和权重，我们还优化了表示校准数据平坦度的项（7-2）。这一术语将鼓励量化模型学习平坦的最小值。因此，AdaRound的传统目标（项（7-1））自然可以更好地概括测试数据（即测试集上的

项（7-2））。此外，我们还应该关注测试数据中的项（7-2），即第2.2节中揭示的

。3.2，术语（7-2）表示利用其在校准数据上的情况的平面度。在这里，我们进一步研究了测试样本的平面度。注意，v（x）从u（x）转换而来，并且该激活量化噪声随输入数据而变化。图2显示了这3种情况的平面度的测试数据和校准数据之间存在差距。根据推论1，这3种情况实际上在数学上引入了不同的u，因此将导致不同的平面度方向，由

给出。对于情况1，在不考虑平面度的情况下，校准期间没有激活量化。
    案例2表明激活扰动完全存在，因此在校准数据上具有良好的平坦性。然而，由于校准数据和测试数据不匹配，情况2极有可能导致过度拟合（更多细节见表8）。情况3，实际上通过降低一些激活量化以及稍微不同的权重扰动来实现最佳表现，并且可能不限于校准数据的平坦度（更多证据可在表9中找到）。这激励我们从一般角度追求一个平坦的最小值，即仅优化校准集上的目标是次优测试集。
    QDROP。受此启发，我们提出QDROP，以进一步增加尽可能多的方向上的平面度。特别是，我们随机禁用并启用每个正向传递的激活量化：

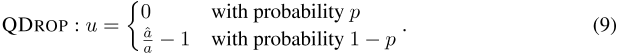
我们将其命名为QDROP，因为它随机丢弃激活量化。理论上，通过随机掩码一些u（x），QDROP可以具有更多样的v（x）并覆盖更多平面度方向，从而使测试样本更平坦，这有助于实现最终的高精度。图3支持我们的分析，其中QDROP比案例3具有更平滑的损失情况，在测试数据的3个案例中获胜。同时，它确实是案例3的细粒度版本，因为案例3以块方式丢弃量化，而我们的QDROP以元素方式操作。
    讨论。QD-ROP可以被视为现有方案的一种广义形式。情况1和2分别对应于p=1和p=0的下降概率。情况3相当于以丢弃概率p=1设置正在优化的块，并且保持其他部分的量化。注意，p服从伯努利分布，因此最大熵可以设为0.5（秦等人，2020），这有助于在各个方向上实现平坦度。
    QDROP易于实现各种神经网络，包括CNN和Transformers，且即插即用，额外的计算复杂度很小。使用QDROP，选择优化顺序的复杂问题，即Sec中的不同情况。3.1，可以避免。


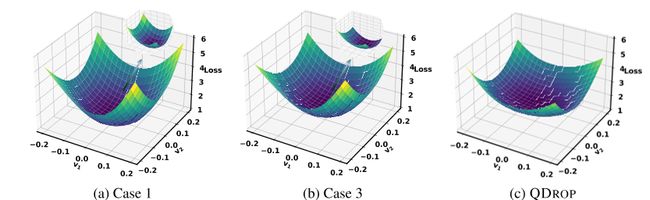
图3:QDROP的量化重量损失面，测试数据和ResNet-18 W3A3的情况1和3。为了更好地区分情况1和3，我们放大了局部损耗面，扰动v 1和v 2幅值为[-0.025,0.025]。

表2:QDROP的影响。

4个实验

    在本节中，我们进行了两组实验来验证QDROP的有效性。以秒为单位。4.1，我们首先对有无下降量化的影响进行消融研究，并分析不同下降率的选择。以秒为单位。4.2，我们将我们的方法与其他现有的视觉和语言任务方法进行了比较，包括ImageNet上的图像分类、MS COCO上的目标检测以及GLUE benchmark和SQuAD上的自然语言处理。
    实施细节。我们的代码基于PyTorch-Paszke等人（2019）。我们将默认丢弃概率设为0.5，除非我们明确提到它。权重调整方法与Nagel等人（2020）相同；李等人（2021a）。每一个块或层输出被重构20k次迭代。对于ImageNet数据集，我们采样1024个图像作为校准集，而COCO使用256个图像。在自然语言处理中，我们采样了1024个示例。除非线性规划任务外，我们还将第一层和最后一层层保留在8位，并采用每通道权重量化。我们使用W4A4表示4位权重和激活量化。更多模型选择和其他设置见附录E。
    但需要注意的是，规则的第一和最后一个层8位意味着8位权重和第一和最后一个层的输入，而B RECQ使用另一个设置，该设置不仅保持第一个层的输入8位，而且还保持第一个层的输出（第二个层的输入）。这确实比常规方法性能更好，只需再保留一个层的8位输入，但在硬件上可能不实用。因此，我们将其与B RECQ的设置进行了比较，以显示我们的方法的优越性，并通过实验提供了一个实用的基线。符号†用于标记B RECQ的设置。

4.1 BLAIN研究

    QDROP的影响。我们提出了QDROP，在这里我们想测试有或没有QDROP的PTQ的效果。我们使用ImageNet分类基准，将权重参数量化为2位，将激活量化为2/4位。如表2所示，QDROP提高了针对ImageNet上6个模型评估的所有位设置的准确性。此外，将QDROP应用于轻型网络架构时，收益更为明显：在W2A4下，MNasNet的增量为2.36%，在W2A2下，RegNet-3.2GF的增量为12.6%。
    下降概率的影响。我们还探讨了PTQ中的丢弃概率。我们在[0,0.25,0.5,0.75,1]中选择p，并在MobileNetV2和RegNet-600MF上进行测试。结果如图5所示。我们发现0.5通常在5个候选者中表现最好。虽然每个ar体系结构都可能有一个细粒度的最佳解决方案，但我们将避免繁琐的超参数搜索，并继续使用0.5。

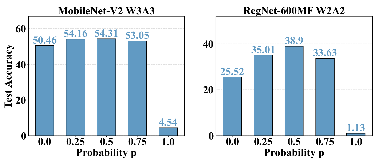
图5：丢弃概率对ImageNet的影响。

4.2文献比较

    ImageNet。我们选择了ResNet-18和-50（He等人，2016年）、MobileNet V2（Sandler等人，2018年）、搜索MNasNet（Tan等人，2019年）和RegNet（Radosavovic等人，2020年）。我们在表3中总结了结果。首先，研究了W4A4量化。可以观察到，QDROP提供0∼ 与包括AdaRound、BRECQ在内的强基线相比，精度提高了3%。
    至于我们的方法与W4A4上的AdaQuant之间的差距，我们认为在量化节点的位置等设置上存在一些离散性，并将这种解释放在第二节中。C、 3。通过W2A4量化，QDROP可以将ResNet-50和RegNet-3.2GF的精度分别提高0.5%和4.6%。此外，为了充分利用QDROP的限制，我们使用2/3位权重和激活进行了更具挑战性的案例。根据表3的最后两行，我们提出的QDROP始终取得了良好的结果，而现有方法的精度下降不可忽略。
    对于W3A3，在MobileNetV2上的差异更大，我们的方法达到了58%的准确性，而B RECQ仅得到23%。在W2A2设置中，PTQ变得更加困难。QDROP在很大程度上超越了竞争方法：ResNet-18上升了12.18%，ResNet-50上升了29.66%，RegNet-3.2GF上升了51.49%。
    可可女士。在这一部分中，我们使用MS COCO数据集验证了QDROP在目标检测任务上的表现。我们使用两阶段更快的RCNN（Ren等人，2015）和一阶段RetinaNet（Lin等人，2017）模型。主干网选自ResNet-18、ResNet-50和MobileNet V2。注意，我们将第一个层和最后一个层设置为8位，并且不量化模型的头部，但是，颈部（FPN）是量化的。实验表明，使用QDROP的W4A4量化几乎不会影响更快的RCNN映射。对于RethinaNet，我们的方法在MobileNetV2主干上有5个映射改进。在低比特设置W2A4中，我们的方法在更快的RCNN和视网膜网络上都有很大的改进，最高可达6.5 mAP。
    GLUE benchmark和SQuAD。我们在自然语言处理任务中测试QDROP，包括GLUE基准和SQuAD1.1。它们都是在典型的非线性规划模型上进行的，即BERT（Devlin等人，2018）。
    与QAT方法（Bai等人，2020）相比，QAT方法通常采用数据增强技巧来实现原始数据的几十倍，我们仅随机提取1024个示例，而无需任何额外的数据处理。除了AdaQuant和B RECQ的精度大大降低外，我们的QDROP在QNLI（8.7%）、QQP（4.6%）和RTE（7.2%）方面优于所有任务。
    至于SST-2，尽管下降量化几乎没有增强，但它确实在4.4%内接近FP32值。对于STS-B，我们认为原始微调模型是用有限的数据进行训练的的，这可能不是很有代表性。
    4.3 R QDROP的稳健性在这一部分中，我们讨论了QDROP在更具挑战性的情况下的有效性，包括更少的数据和跨域情况。关于校准数据的大小，我们考虑了另外4种选择。可以观察到，在每种设置下，减少一些量化表现更好，甚至与没有减少一半原始校准数据相当。受Yu等人（2021）的启发，我们还通过1024个例子从域外数据重构块输出，即CIFAR100（Krizhevsky等人，2009）、MS COCO和ImageNet上的测试。结果见表6，其中我们的QDROP仍然稳定工作。

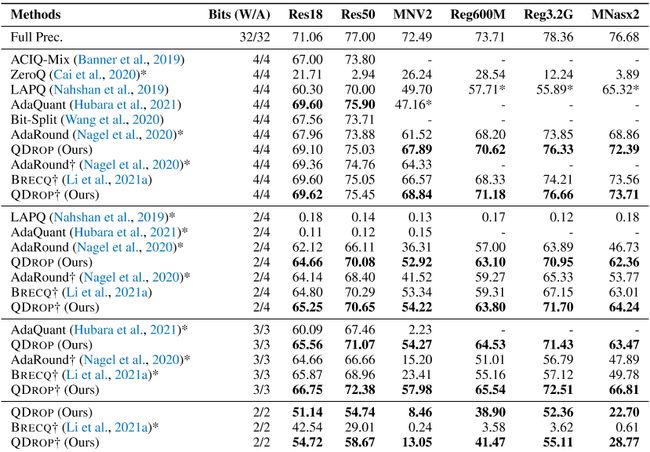
表3:ImageNet上具有低比特激活的不同训练后量化策略的准确性比较。*表示我们根据开源代码实现的†意味着使用B RECQ的第一和最后一个层8位设置，除了第一和最后一个层中的输入和权重外，还保留第一个层的输出8位。

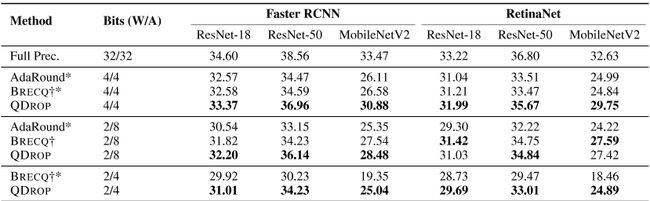
表4:MS COCO上典型训练后量化策略的mAP比较。请注意，对于B RECQ，我们没有对头部进行量化，并将主干中的第一和最后一个层保持为8位。其他符号与表3一致。

表5:NLP任务与E8W4A4上其他方法的表现比较。在这里，我们使用符号EeWwAa额外表示嵌入位，并在GLUE和SQuAD1.1上进行实验。

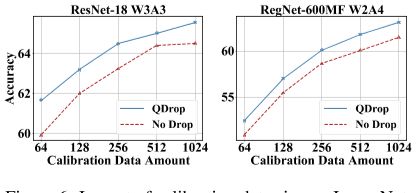
图6：校准数据大小对ImageNet的影响。

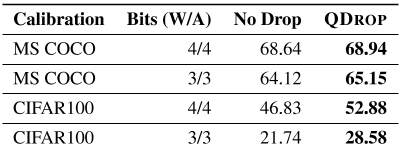
表6：跨域数据。

5结论

    在本文中，我们介绍了QDROP，一种新的训练后量化机制。QDrop旨在通过一个微小的校准集实现良好的测试精度。这是通过朝着平坦的极小值进行优化来实现的。我们将PTQ目标从理论上分解为平面度问题，并从一般角度改进平面度。我们全面验证了QDROP在各种任务上的有效性。它可以实现几乎无损的4位量化网络，并可以显著改善2位量化结果。

致谢

    我们衷心感谢匿名评论者的认真评论和宝贵建议，以使这一点更好。我们感谢张和陈对这项工作的帮助。
    这项工作得到了国家自然科学基金62022009和61872021的部分资助，青年学者感觉时间研究基金，以及北京Nova科技计划Z19110000119050的部分资助。

参考文献

Haoli Bai, Wei Zhang, Lu Hou, Lifeng Shang, Jing Jin, Xin Jiang, Qun Liu, Michael Lyu, and Irwin King. Binarybert: Pushing the limit of bert quantization. arXiv preprint arXiv:2012.15701 , 2020.

Ron Banner, Yury Nahshan, and Daniel Soudry. Post training 4-bit quantization of convolutional networks for rapid-deployment. In Advances in Neural Information Processing Systems , 2019.

Yaohui Cai, Zhewei Yao, Zhen Dong, Amir Gholami, Michael W Mahoney, and Kurt Keutzer. Zeroq: A novel zero shot quantization framework. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition , pp. 13169–13178, 2020.

Yoni Choukroun, Eli Kravchik, Fan Yang, and Pavel Kisilev. Low-bit quantization of neural net- works for efficient inference. In ICCV Workshops , pp. 3009–3018, 2019.

Jacob Devlin, Ming-Wei Chang, Kenton Lee, and Kristina Toutanova. Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint arXiv:1810.04805 , 2018.

Laurent Dinh, Razvan Pascanu, Samy Bengio, and Yoshua Bengio. Sharp minima can generalize for deep nets, 2017.

Zhen Dong, Zhewei Yao, Yaohui Cai, Daiyaan Arfeen, Amir Gholami, Michael W Mahoney, and Kurt Keutzer. Hawq-v2: Hessian aware trace-weighted quantization of neural networks. arXiv preprint arXiv:1911.03852 , 2019.

Steven K Esser, Jeffrey L McKinstry, Deepika Bablani, Rathinakumar Appuswamy, and Dharmen- dra S Modha. Learned step size quantization. arXiv preprint arXiv:1902.08153 , 2019.

Angela Fan, Pierre Stock, Benjamin Graham, Edouard Grave, Rémi Gribonval, Herve Jegou, and Armand Joulin. Training with quantization noise for extreme model compression. arXiv preprint arXiv:2004.07320 , 2020.

Pierre Foret, Ariel Kleiner, Hossein Mobahi, and Behnam Neyshabur. Sharpness-aware minimiza- tion for efficiently improving generalization. arXiv preprint arXiv:2010.01412 , 2020.

Yonggan Fu, Qixuan Yu, Meng Li, Vikas Chandra, and Yingyan Lin. Double-win quant: Aggres- sively winning robustness of quantized deep neural networks via random precision training and inference. In International Conference on Machine Learning , pp. 3492–3504. PMLR, 2021.

Song Han, Huizi Mao, and William J Dally. Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding. arXiv preprint arXiv:1510.00149 , 2015.

Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recog- nition. In Proceedings of the IEEE conference on computer vision and pattern recognition , pp. 770–778, 2016.

Geoffrey Hinton, Oriol Vinyals, and Jeff Dean. Distilling the knowledge in a neural network. arXiv preprint arXiv:1503.02531 , 2015.

Sepp Hochreiter and Jürgen Schmidhuber. Flat minima. Neural computation , 9(1):1–42, 1997.

Itay Hubara, Yury Nahshan, Yair Hanani, Ron Banner, and Daniel Soudry. Accurate post training quantization with small calibration sets. In International Conference on Machine Learning , pp. 4466–4475. PMLR, 2021.

Pavel Izmailov, Dmitrii Podoprikhin, Timur Garipov, Dmitry Vetrov, and Andrew Gordon Wil- son. Averaging weights leads to wider optima and better generalization. arXiv preprint arXiv:1803.05407 , 2018.

Benoit Jacob, Skirmantas Kligys, Bo Chen, Menglong Zhu, Matthew Tang, Andrew Howard, Hartwig Adam, and Dmitry Kalenichenko. Quantization and training of neural networks for efficient integer-arithmetic-only inference. In Proceedings of the IEEE conference on computer vision and pattern recognition , pp. 2704–2713, 2018.

Yiding Jiang, Behnam Neyshabur, Hossein Mobahi, Dilip Krishnan, and Samy Bengio. Fantastic generalization measures and where to find them. arXiv preprint arXiv:1912.02178 , 2019.

Prad Kadambi, Karthikeyan Natesan Ramamurthy, and Visar Berisha. Comparing fisher information regularization with distillation for dnn quantization. 2020.

Nitish Shirish Keskar, Dheevatsa Mudigere, Jorge Nocedal, Mikhail Smelyanskiy, and Ping Tak peter Tang. On large-batch training for deep learning: Generalization gap and sharp minima. arXiv preprint arXiv:1609.04836 , 2016.

Alex Krizhevsky, Geoffrey Hinton, et al. Learning multiple layers of features from tiny images. 2009.

Yuhang Li, Xin Dong, and Wei Wang. Additive powers-of-two quantization: An efficient non- uniform discretization for neural networks. arXiv preprint arXiv:1909.13144 , 2019.

Yuhang Li, Ruihao Gong, Xu Tan, Yang Yang, Peng Hu, Qi Zhang, Fengwei Yu, Wei Wang, and Shi Gu. Brecq: Pushing the limit of post-training quantization by block reconstruction. arXiv preprint arXiv:2102.05426 , 2021a.

Yuhang Li, Mingzhu Shen, Jian Ma, Yan Ren, Mingxin Zhao, Qi Zhang, Ruihao Gong, Fengwei Yu, and Junjie Yan. MQBench: Towards reproducible and deployable model quantization benchmark. In Thirty-fifth Conference on Neural Information Processing Systems Datasets and Benchmarks Track (Round 1) , 2021b. URL https://openreview.net/forum?id=TUplOmF8DsM .

Yuhang Li, Feng Zhu, Ruihao Gong, Mingzhu Shen, Xin Dong, Fengwei Yu, Shaoqing Lu, and Shi Gu. Mixmix: All you need for data-free compression are feature and data mixing. In Proceedings of the IEEE/CVF International Conference on Computer Vision , pp. 4410–4419, 2021c.

Tsung-Yi Lin, Priya Goyal, Ross Girshick, Kaiming He, and Piotr Dollár. Focal loss for dense object detection. In Proceedings of the IEEE international conference on computer vision , pp. 2980–2988, 2017.

Markus Nagel, Mart van Baalen, Tijmen Blankevoort, and Max Welling. Data-free quantization through weight equalization and bias correction. In Proceedings of the IEEE/CVF International Conference on Computer Vision , pp. 1325–1334, 2019.

Markus Nagel, Rana Ali Amjad, Mart Van Baalen, Christos Louizos, and Tijmen Blankevoort. Up or down? adaptive rounding for post-training quantization. In International Conference on Machine Learning , pp. 7197–7206. PMLR, 2020.

Yury Nahshan, Brian Chmiel, Chaim Baskin, Evgenii Zheltonozhskii, Ron Banner, Alex M Bronstein, and Avi Mendelson. Loss aware post-training quantization. arXiv preprint arXiv:1911.07190 , 2019.

Behnam Neyshabur, Srinadh Bhojanapalli, David McAllester, and Nathan Srebro. Exploring generalization in deep learning, 2017.

Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, et al. Pytorch: An imperative style, high-performance deep learning library. Advances in neural information processing systems , 32: 8026–8037, 2019.

Haotong Qin, Ruihao Gong, Xianglong Liu, Mingzhu Shen, Ziran Wei, Fengwei Yu, and Jingkuan Song. Forward and backward information retention for accurate binary neural networks. In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) , June 2020.

Ilija Radosavovic, Raj Prateek Kosaraju, Ross Girshick, Kaiming He, and Piotr Dollár. Designing network design spaces. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition , pp. 10428–10436, 2020.

Shaoqing Ren, Kaiming He, Ross Girshick, and Jian Sun. Faster r-cnn: Towards real-time object detection with region proposal networks. In Advances in neural information processing systems , pp. 91–99, 2015.

Olga Russakovsky, Jia Deng, Hao Su, Jonathan Krause, Sanjeev Satheesh, Sean Ma, Zhiheng Huang, Andrej Karpathy, Aditya Khosla, Michael Bernstein, Alexander C. Berg, and Li Fei-Fei. ImageNet Large Scale Visual Recognition Challenge. International Journal of Computer Vision (IJCV) , 115(3):211–252, 2015. doi: 10.1007/s11263-015-0816-y.

Mark Sandler, Andrew Howard, Menglong Zhu, Andrey Zhmoginov, and Liang-Chieh Chen. Mo- bilenetv2: Inverted residuals and linear bottlenecks. In Proceedings of the IEEE conference on computer vision and pattern recognition , pp. 4510–4520, 2018.

Mingzhu Shen, Feng Liang, Ruihao Gong, Yuhang Li, Chuming Li, Chen Lin, Fengwei Yu, Junjie Yan, and Wanli Ouyang. Once quantization-aware training: High performance extremely low- bit architecture search. In Proceedings of the IEEE/CVF International Conference on Computer Vision , pp. 5340–5349, 2021.

Mingxing Tan, Bo Chen, Ruoming Pang, Vijay Vasudevan, Mark Sandler, Andrew Howard, and Quoc V Le. Mnasnet: Platform-aware neural architecture search for mobile. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition , pp. 2820–2828, 2019.

Peisong Wang, Qiang Chen, Xiangyu He, and Jian Cheng. Towards accurate post-training network quantization via bit-split and stitching. In Proc. 37nd Int. Conf. Mach. Learn.(ICML) , 2020.

Dongxian Wu, Shu-Tao Xia, and Yisen Wang. Adversarial weight perturbation helps robust gener- alization. arXiv preprint arXiv:2004.05884 , 2020.

Guandao Yang, Tianyi Zhang, Polina Kirichenko, Junwen Bai, Andrew Gordon Wilson, and Chris De Sa. Swalp: Stochastic weight averaging in low precision training. In International Conference on Machine Learning , pp. 7015–7024. PMLR, 2019.

Haichao Yu, Linjie Yang, and Humphrey Shi. Is in-domain data really needed? a pilot study on cross-domain calibration for network quantization. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR) Workshops , pp. 3043–3052, June 2021.

Xiangguo Zhang, Haotong Qin, Yifu Ding, Ruihao Gong, Qinghua Yan, Renshuai Tao, Yuhang Li, Fengwei Yu, and Xianglong Liu. Diversifying sample generation for accurate data-free quan- tization. In The IEEE Conference on Computer Vision and Pattern Recognition (CVPR) , June 2021a.

Xiangguo Zhang, Haotong Qin, Yifu Ding, Ruihao Gong, Qinghua Yan, Renshuai Tao, Yuhang Li, Fengwei Yu, and Xianglong Liu. Diversifying sample generation for accurate data-free quantiza- tion. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition , pp. 15658–15667, 2021b.

Yaowei Zheng, Richong Zhang, and Yongyi Mao. Regularizing neural networks via adversarial model perturbation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition , pp. 8156–8165, 2021.

Barret Zoph and Quoc V Le. Neural architecture search with reinforcement learning. arXiv preprint arXiv:1611.01578 , 2016.