软件工程 黄金点游戏

这个故事最初出现在 《移山之道》中，我经常拿来做和创新的时机相关课堂练习和讨论，效果很好。我把这个练习和它的一些延伸话题都搬到这个新博客里。

黄金点游戏

N个同学（N通常大于10），每人写一个 0~100之间的有理数 (不包括0或100)，例如：10.5， 75， 等，交给裁判。 裁判算出所有数字的平均值，然后乘以 0.618（所谓黄金分割常数），得到黄金点 （Golden Number）的值。提交的数字最靠近Golden Number - G（取绝对值）的同学得到 N 分，离 G最远的同学得到－2分，其他同学得 0 分。

玩了几次以后，大家发现了一些很有意思的现象，比如黄金点在逐渐地往下移动。

如果你和其他20 个和你智力水平类似的人玩这个游戏, 你会选择什么数字呢？

[现在请记下你的数字, 以后不能改]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
【上面有意留下空白，让你思考】

你会想, 如果大家随机报数的话, 0-100 的平均数是50, 50 * 0.618 = 31. 那我就来个 31。

但是其他人也不是傻子, 他们肯定也想到了这一点。如果大家都选 31 附近的数, 那我得选 31*0.618 = 19;

但是这些人肯定也想到了这一点, 那我要选 19 * 0.618 = 12… 然后 12 * 0.618 = 8 … 然后一直向下发展 …

最后干脆选 0.0001 好了！

0.0001 是正确答案么? 这取决于参与游戏的所有成员。大家想得这么远么，想得远，能做到么？

来源

这个游戏不是我发明的, 有记录的最早的实践是经济学家 Richard Thaler 在1997年通过英国《金融时报》给读者出的一道题目（见下图）。当时没有用黄金点，而是 2/3 这个分数。 2017 年， Thaler 教授因为在行为经济学方面的研究而获得诺贝尔经济学奖。

我第一次玩这个游戏是 2006 年和华宏伟老师，黄雪斌老师在清华软件学院的一个软件工程的（MS^2）培训班上。我觉得很有意思，后来这个游戏就成了我 “现代软件工程” 课的固定节目, 在不少大学的计算机系都玩过。有一年春节我们研究院一个叫 nullgate 的同事抽中夏威夷旅游大奖，但是他决定让出, 我们部门也使用这个办法来决定幸运者。

根据我多次观察（在几十所高校和几十次聚会上玩过）, 第一次游戏的获胜数字和大家的聪明程度有关，越聪明，第一轮的数字就越低。在中国一流高校，第一轮获胜的数字一般在下面这个数字附近:

17

从17 这个数字我们可以推出，游戏者们进行了两次迭代 （50 * 0.618 * 0.618 = 19.096）。如果继续玩下去, 这个数字会变么? 虽然说两次游戏之间没有任何联系, 是概率中的独立事件, 但是前一次游戏的 G-number 给了所有参与者一个强大的暗示， 以后游戏的G-number 一定会向下走。 下面是清华姚班 2008 年秋季学期一个叫 “贝爷” 的 TA 给连续12次游戏做的记录，从趋势看, 数值会逼近0, 但是变化也不是一帆风顺的, 每次触底之后, 就会小小反弹一下。

感想

赢者通吃

参加游戏的人都是在top N 的大学生, 或者IT 从业人员, 数学足够好, 都是聪明人。我把题目公布之后, 一些人马上就说– 这肯定收敛到0啦！ 他们交上来一个 (0.00001 ) 的答案 (提交的数字必须大于 0 )。遗憾的是, 一起玩游戏的人其他人不这么想。 一个小团体, 或者一个小社会的社会共识 (consensus) 从来不是最激进的, 每个个体发出自己看似随机的声音, 它的进步是缓慢的, 有时还倒退一下。 如果只看微博上的发言, 你会觉得德先生和赛先生早已是国人的共识; 如果只参加最前沿的科技沙龙, 你会觉得明天大家都会用人体嵌入AI智能芯片同时会同步电子书邮件微博微信SNS再加GPS再有云计算，你如果不推出相应产品就会被淘汰… 但是社会作为一个整体还没有进步得这么快。

那些成功的企业只是比大众的平均值先走了一小步（平均值 * 0.618）, 就是这一小步, 让大部分人看到了产品的“相对优势”从而接受产品。关于技术创新, 一些趋势（例如社会网络），大家早就看到了, 也有一些产品推出, 但是往往最后成功的产品成功在时机上。 一本很有名的书 - Cross The Chasm 描述了大众对新技术接受的曲线, 曲线下面的面积大致对应人数。大众平均值的0.618 就在 “Early Adopter” 那里, 有时一个崭新的技术, 推出的时机太早 (它的值比G-number 小一点), 它就跨不过那道沟 (Chasm).

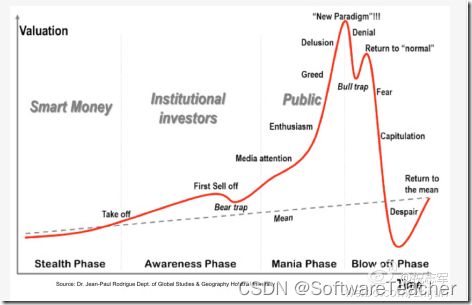
Technology Hype Cycle

说到时机, 任何新技术都有一个自身发展的规律，Gartner 的Jackie Fenn 写了一个很有意思的报告, 提到了Technology Hype Cycle。

随着一个新技术经历不同的阶段, 公众对它的期望值, 炒作值也有很大的差别.

1）技术触发期 （技术走出实验室, 天使投资, 第一轮产品出现, 尝鲜者试用）

2）期望膨胀期（博客/微博/媒体炒作, 泡沫达到最大, 大众开始跟进, 负面报道出现）

3）迷茫期 (开始整合, 第二/三轮融资, 但是只有5% 的目标用户正式使用产品，第二版产品出现)

4）低调发展期 （漫长的低调发展, 最佳的方法和实践开始出现, 第三代产品出现, 易用性, 和其他产品的整合更好）

5）主流发展期 (成为成熟的技术, 市场以20-30% 的速度成长)

很多大家正在使用的“新颖“产品, 往往是经历了迷茫期之后的二代产品, 那些在泡沫最大的时候匆忙出现的第一代的产品大多数都没有等到这一天 (电子书, 平板电脑，社会网络等)。

现在技术圈子里大家都在吹的那些技术 SoLoMo，Cloud，AI等等, 它们处于哪一个阶段? 你应该贸然出手么？

和上图相对应的是一个高科技公司股价变化图, 炒股票在短期内是一个群体在估计下一个数字的游戏。 从图表中你可以看到sell off, media, enthusiasm，greed, fear， dispair 等种种因素在起作用, 耳语效应， 从众效应都在推波助澜，根据这个表, 你心仪的公司处于哪一个阶段? 你要买入还是抛售?

Interpersonal Awareness & Social Awareness

说着说着就扯远了, 进入了我不熟悉的领域，大家姑妄听之。。。

科学家认为，俺们人类有别于其他动物的最大特点是俺们大脑里有发达的部分，处理“别人在做什么“ 和 ”未来会发生什么“这些事情。能摆脱 [自我/当下] 而考虑到[别人/将来], 从而主动地为群体和将来行动， 这是人和其他动物不同的地方（来源: http://www.pbs.org/wnet/humanspark/）。能在一个群体中审时度势, 拉帮结派，尔虞我诈，选择时机出手, 俺们人类的确太擅长了。

在一些大型的软件跨国企业, “Interpersonal Awareness” 是员工素质的一个重要部分, 把它放到“黄金点游戏“这个场景中, 你得了解一屋子的同学大概是在想什么，你如何影响他们, 你才能有获胜的希望。每个人独立埋头推导公式, 是得不出获胜的数字的。

国外还有 Social awareness + emotional skills = successful kids 的说法, 据说此类教育在小孩到了高中甚至成年都有积极的影响。有意思的是，他们没有提到“奥数“ 对小孩将来的影响。

反过来看, 天朝的同学们从小就被灌输“搞好自己的学习就可以了“， ”把考试考好, 以后就好了“– 但是从来没有让同学们考虑目前的死记硬背和将来是什么关系。

一个软件团队, 如果大家都不考虑“别人“, “未来”， 光是每个人独立地搞自己眼前的一摊事, 是不行的, 把自己的代码重构出花来也不行，把SCRUM （史克朗姆）玩到极限也不行。 这也是我觉得聪明的同学们欠缺较多的地方。 所以《现代软件工程》课包括了很多”两人合作”, ”黄金点游戏“, 还有”估算工作量“等练习。

作业

这个游戏可以变成一个持续发展的团队项目：

1. 在课堂上玩这个黄金点游戏，用Excel 纪录成绩。过渡到做成简单的单机版游戏，锻炼基本的编程能力

2. 两人合作，做成简单的 client/server App，用户从网页/手机上输入数字，并算出获胜者。 技术讨论的议题有：
   前面写的模块有多少是可以重用的？ 为何不能重用？
   研讨 client/server 的API 应该怎么设计，如何认证用户？
   如何开发client App
   为了保证游戏按时完成，如何在服务器/客户端做时钟同步？
   如果获得第一名的多个用户的数字相同，如何排定次序？(提示：可以考虑提交时间，历史成绩)

3. 如何设计测试用例， 保证server 的正确性， 效率， 压力测试 (如何模拟上千个客户端，从不同的端口，提交不同的数字？)

4. 原来我们是让用户从客户端输入数字， 看到结果之后，再玩下一轮。用户玩这个游戏是有一定的策略的， 我们如何能把这个策略变成程序，成为人工智能呢？ 能否利用 AI 算法提交数据？
   　client 程序能访问所有以前的历史记录， 它再推测下一个数字是多少， 然后提交。

这里面也有很多问题要克服，例如，如果数字很小 0.00000000000000000001, 下溢了， 怎么办？
应该提交的是 double, float, 还是 string 类型？

5. 全班同学每人写一个程序， 玩一万轮， 服务器要能快速处理。
   　　挑战：
   　　如何在服务器和客户端都做到高效， 能多少秒钟就比完一轮， 并把数据传给所有客户端？ 客户端是通过什么接口来接受比赛数据，或者从某个公共来源去读取数据？
6. 修改规则， 每个用户每次可以提交两个数字， 其他规则一样，再玩一万轮。

挑战：这个时候，有程序会不会提交一个大的数字，来保证自己的另一个数字比较接近 golden number? 你的AI 程序如何在这个新规则下占得先机？
7) 让互联网的用户可以通过网站注册， 然后用某种 Domain Specified Language 写这个AI 的规则， 然后他们也可以通过网站玩这个游戏。
　　挑战： 设计这种 DSL，并解释执行。

例如， DSL 可以支持下面的规则：

① 我每一轮都提交上一轮所有数字的平均值 * 0.618 * 0.618

② 如果我上一轮的提交的数值小于当轮的 golden number，那我的下一个数字要是上个数字的两倍

8. 扩展到全球，服务器能 24/7 不断主持游戏，并记录成绩。 同时，全球用户的数据都可以开放下载，供人工或者是 AI 做研究和训练。
   　　挑战：这个过程就能练很多技能和软工设计的功夫， 同时可以让各个开发人员的AI 上台来比拼。

（原文：https://www.cnblogs.com/xinz/archive/2011/08/08/2130505.html）