图深度学习_谱图论和图上的信号处理

谱图论和图上的信号处理

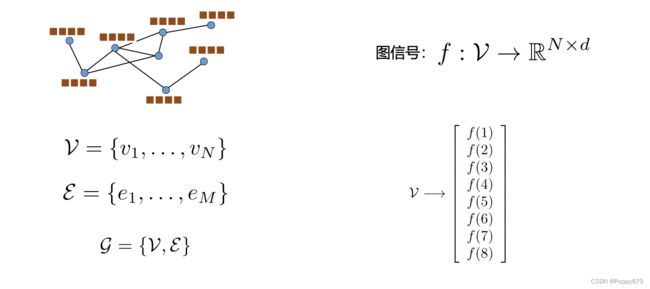
图信号，即图数据结构中存在的与节点相关联的特征或属性，它捕获结构信息（或节点之间的连接）和数据（或节点上的属性）。
当图中节点是一维信号时，对这样的图处理是直接将节点映射到向量，$f_1$是节点1的信号，$f_n$是节点n的信号，那么就可以通过$f$来把一维信号拓展到多维。

图最常见的表示方式：邻接矩阵
此外还有度矩阵：一个对角矩阵，所有其他节点都为0，只有对角线上为非0。对角线上的元素对应相对应节点的度
度矩阵表示：$\mathbf{D}=\mathrm{diag}($ degree $\left(v_1\right),\dots ,\mathrm{degree}\left(v_N\right))$

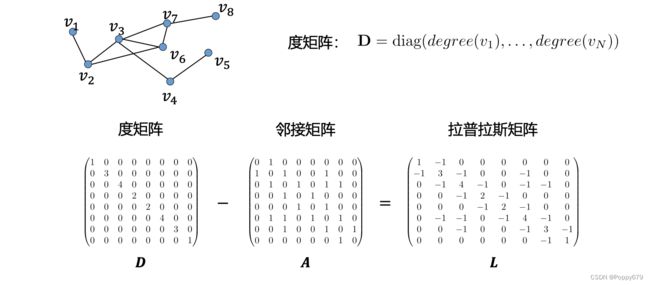
拉普拉斯矩阵是谱图论的重要表示方式
拉普拉斯矩阵可以作为一个差分算子：测量当前节点$i$信号和节点$j$信号差别的和，$j$是$i$的邻居。

$\mathbf{h}=\mathbf{L}\mathbf{f}=(\mathbf{D}-\mathbf{A})\mathbf{f}=\mathbf{D}\mathbf{f}-\mathbf{A}\mathbf{f}$
$\mathbf{h}(i)={\sum }_{v_j\in \mathcal{N}\left(v_i\right)}(\mathbf{f}(i)-\mathbf{f}(j))$

但是信号之间的差距是有正有负，存在正负抵消的情况。所以常用拉普拉斯二次型：用于衡量所有节点对之间的信号差别。

${\mathbf{f}}^T\mathbf{L}\mathbf{f}=\frac{1}{2}{\sum }_{i,j=1}^N\mathbf{A}[i,j](\mathbf{f}(i)-\mathbf{f}(j){)}^2$

拉普拉斯二次型整体衡量的就是$f$在图信号上的光滑度或频率。相邻节点差距很小，那么频率就很低；相邻节点差距很大，那么频率就很高。（频率就是相似性的意思？）
在上述公式中，$f$是一个向量，$f$非0，那么等式右边一定大于0。因此可以得到拉普拉斯二次型是一个半正定矩阵。

半正定矩阵：对于任何非0向量，使用二次型得到的值都是非负的话，称这个矩阵是半正定矩阵.

对于半正定矩阵，可以进行矩阵分解。半正定矩阵事一个n维的方阵的话，那么就有n个特征向量，对应n个特征值。

拉普拉斯矩阵的特征分解
拉普拉斯矩阵有一套完整的标准正交的特征向量。
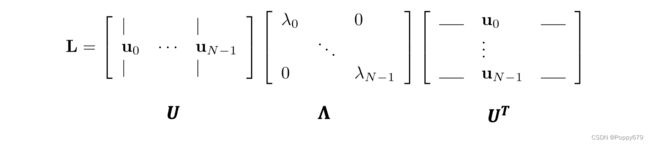通常将这些特征向量按照特征值从小到大排列

$0={\lambda }_0<{\lambda }_1\le \cdots {\lambda }_{N-1}$

矩阵$U$是一个正交矩阵，是特征向量作为列向量的特征矩阵, $\mathbf{\Lambda }$是一个对角矩阵，是所有特征值组成的对角矩阵。因为每个特征向量是n维的，可以把每个特征向量看成是图上的信号。信号的特点：

频率：${\mathbf{u}}_i^T\mathbf{L}{\mathbf{u}}_i={\mathbf{u}}_i^T{\lambda }_i{\mathbf{u}}_i={\lambda }_i$

频率对应特征值，那么如果把特征向量看作图上的一个一维信号，信号的光滑程度就可以用信号的特征值来衡量。

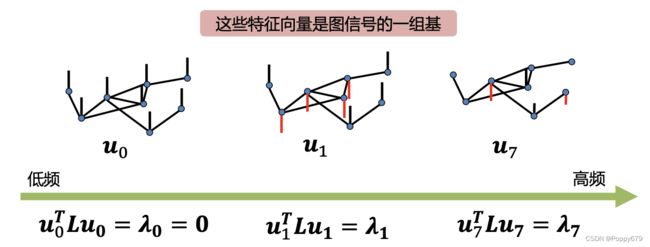
特征向量是正交的，那么可以组成一个n维的空间。

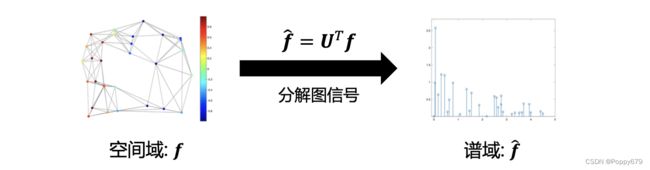
图傅立叶变换（GFT）

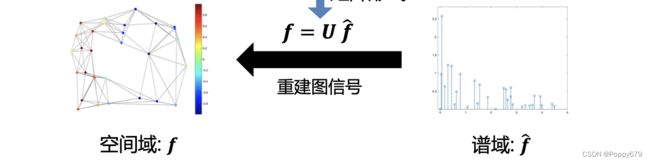
任意的图信号$f$可以用图傅立叶级数表示

$\mathbf{f}={\sum }_{i=0}^{N-1}{\hat{f}}_i\cdot {\mathbf{u}}_i$

${\hat{f}}_i={\mathbf{f}}^{\top }{\mathbf{u}}_i$

${\mathbf{u}}_i$是基，即特征向量， ${\lambda }_i$是基的频率，即特征值， ${\hat{f}}_i$ 是傅立叶系数。

空间域–傅立叶变换–>谱域

空间域：图的拓扑结构
谱域：空间对应的傅立叶系数
空间域<–傅立叶逆变换–谱域