第十九周工作进展报告 Local Differential Privacy for Deep Learning

第十九周工作进展报告

本周主要是学习联邦学习与隐私保护中的一种用于深度学习框架下的本地差分隐私方法以及一种SGD-DP（stochastic gradient descent differential privacy）算法。

“Local Differential Privacy for Deep Learning”文中预备知识介绍：

1）隐私预算（privacy budget）/隐私损失（privacy loss）：ε

2）错误概率（probability of error）/失败概率（probability of fail）：δ是说明可能导致高隐私损失的“不良事件”的参数。为了将隐私损失降低，必须保持在较低的值。例如：当时，发生不良事件的概率为1%。

3）差分隐私的定义：

4）本地差分隐私的定义[10]：

5）随机响应（randomized response）：随机想用通过随机化结果“是”或“否”的回答来消除逃避型的答案偏差。丢硬币的例子：当第一次硬币朝上（正面）时，回答真实答案，当第一次硬币反面时，扔第二次硬币，当第二次硬币朝上（正面）时，回答“是”，当第二次硬币反面时，回答“否”。假设使用了偏置硬币（a biased coin），回答真实答案的概率为p，回答错误答案的概率为(1-p)。则当时，提供ε-DP。

6）灵敏度(sensitivity)：定义为单个个体对数值查询结果的最大影响。。

7）RAPPOR(randomized aggregatable privacy-preserving ordinal response)：谷歌提出的LDP算法。在全局灵敏度定义中，x和y为相邻输入，在RAPPOR算法中，任何输入vi都被编码成d比特的向量，每个d比特向量都包含d-1个0和1个1，所以Δf的最大值为2比特。换句话说，RAPPOR的灵敏度f为2。当在随机化中保留原始特别的真实值的概率p如下时，RAPPOR是一种LDP算法：

8）z-score标准化为：经过处理的数据符合标准正态分布，即均值为0，标准差为1。其转化函数为x*=x-μσ，其中μ为所有样本数据的均值，σ为所有样本数据的标准差。Z-score标准化方法适用于属性A的最大值和最小值未知的情况，或有超出取值范围的离群数据的情况。该标准化方法要求原始数据的分布可以近似为高斯分布，否则效果会变得很糟糕。

 

在“Local Differential Privacy for Deep Learning”一文中指出，传统差分隐私一般都是GDP（global differential privacy），而GDP需要一个可信任的管理者对真实结果加噪声然后返回给请求者，其常用的是拉普拉斯机制和高斯机制，但这两种机制对于DL（deep learning）来说可能是复杂的，不确定的，并产生不太准确的结果或带来更高程度的隐私泄露。所以，文中给出一种本地差分隐私LDP的方法（local differential privacy），并称其为LATENT算法，LATENT运用在卷积神经网络中，在数据离开设备之前添加随机化层的结构，无需一个可信任的第三方，而且其中的随机化层中采用了一种新的LDP协议，与现有的LDP协议相比，它允许潜在用户保持较高的效用。该算法在低隐私预算的情况下（ε=0.5），具有较高的模型精度，GDP和LDP的区别如图1所示。

 

图1 GDP和LDP的区别

 

常见的CNN模型结构如下图2，卷积层（convolution）和池化层（pooling layers）用于降低维度，池化层后的是一个Flattening层，用于将数据展平成一个相当大的1维向量，利用这个向量，输入全连接人工神经网络中（ANN），即全连接层。

 

图2 通用CNN网络模型结构

 

而文中所提算法的网络模型结构如下图3所示，将差分隐私作为中间层，放入CNN网络中。即在卷积模块（CNM）和FC模型（FCN）之间插入一个LATENT随机化模块。初始时，使用卷积层和池化层对输入特征进行降维处理，最终池化层的输出是一个单1维向量。

在随机化前，LATENT将输入值转换为二级制值。输入值可能有不同范围，转换大的值或小的值为二进制可能设计大量的位，这可能对算法引入不同的复杂性，为了避免这种复杂性，文中对1维向量进行z-score标准化处理。

 

图3 文中所提算法网络模型结构

 

特定的输入需对上界和下界进行初步估计。下图4显示z-score标准化输入的二进制转换的位的排列。二进制字符串有三个主要段。第一位表示输入的符号（1表示负，0表示正），另两位分别是整数部分和小数部分。选择整数位取决于整数的最大值，由于z-score标准化，表示整数所需的比特位很小；表示小数位的比特数取决于精度，为了获取更高的精度，小数部分需要使用更多的位。

 

图4 浮点数或证整数到二级制数的直接映射

 

二进制表示也可以根据以下公式生成，n代表整数部分的二进制位数，m代表小数部分的二进制位数，x为原始输入，g(i)表示二进制字符串的ith位（第i位），当k=-m时，表示最低有效位。

同时，文中提出合并二进制字符串以减少隐私损失，如果分别对每个二进制字符串做随机化的话，将增加所有随机化步骤的隐私预算。如果我们对r个二进制字符串分别进行随机化，将会产生r×ε隐私损失。

文中具体实验中，选用的数据集为MNIST和CIFAR-10。对于MNIST数据集的实验，epoch为12，batchsize为128，训练集准确率99.25%，测试集准确率98.16%，在LATENT层中，使用10位（bits），4位整数，5位小数，1位符号数；对于CIFAR-10数据集的实验，epoch为100，batchsize为32，训练集准确率73.32%，测试集准确率78.75%，在LATENT层中，使用10位（bits），2位整数，7位小数，1位符号数（我的理解：这个数据集和网络模型更复杂，需要更高的精度，所以小数位数更多）。

文中提出的具体网络模型结构如图5所示，绿色箭头表示使用相同的配置，黄色部分为文中所提的LATENT随机化模块。文中所提算法与现有算法的性能对比如表1所示。

图5 左边为在MNIST数据集中的模型结构（包括有使用差分隐私和不使用差分隐私），右边为在CIFAR-10数据集中的模型结构

 

 

表1 LATENT算法与现有算法的性能对比

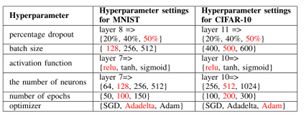
另外，文中提出提高模型精度的超参数调整方法，需要调整的参数为：不同的百分比的dropouts，不同的batchsize、激活函数、神经元个数、优化器、epoch数，参数的具体数值选择图表2所示，红色标识的为最佳参数值。同时，文中提出提高模型精度的图像增强的方法，对图像0.1%的总宽度随机平移、0.1%的总高度随机垂直移动、10度的随机旋转、随机水平翻转。

 

表2 超参数调整的具体数值

 

小结：调查降低敏感度的可能性将是一个很好的研究途径，低敏感度将允许选择合适领域要求的适当ε值。而文中所提方法是将整个完整的CNN网络拆开，再添加新的随机化模块，但若想完整训练模型，则需要本地端和服务器端都保证完成训练工作，一旦中途出现断连情况，网络训练无法进行。另外，当本地参与者的数量增加时，网络的训练参数量就会变得非常大。此外，在一些没有全连接层的网络中，这个方法就不适用了，有一定的局限性，相比之下，联邦学习能解决上述问题。但文中提出的一些增加灵敏度的方法适合用于提升其他差分隐私方法的精度，例如：将输入值转换为二级制值以及合并二进制字符串等方法。

 

在“Deep Learning with Differential Privacy”一文中，提出了结合差分隐私的深度学习算法，并在差分隐私的框架内对隐私成本进行了精细分析，实现在适度的隐私预算下，以可控的软件复杂性、训练效率和模型质量成本下，训练具有非凸目标的深度神经网络。

文中提出独立训练样本计算梯度的高效算法，将任务分成小堆，输入层使用差分隐私策略投影。该方法有三个主要步骤：一个差分隐私随机梯度下降（SGD）算法，the moment accountant和超参数调整。

其中差分隐私随机梯度下降（SGD）算法步骤为：（1）输入：，损失函数：，参数：学习率，噪声等级（界限）σ，组大小（group size）L，梯度范数界限（gradient norm bound）C；（2）初始化：（随机初始化）；（3）循环执行（）：①随机抽样，抽样概率为，②计算梯度：对于每一个计算其梯度，；③剪切梯度：（其中梯度裁剪是解决梯度爆炸的一种技术）；④添加噪声：；⑤梯度更新：。（4）输出：θT和计算所有的隐私成本（privacy cost ）。

其中算法中将任务分成小堆称为Lots：分组，像普通的SGD算法一样，文中的算法通过计算一组例子的梯度并取平均估算L的梯度。这个平均值提供了一个无偏差的估算值，它的变化随着数据量的增加迅速减少。称这个组合为lot，与通常的计算组合batch区别开。为了限制内存消耗，设置batch的容量远小于lot，batch是算法的参量。对batch进行计算，然后将batch放在一个lot中为了添加噪声。（我的理解是一个batch添加一次噪声）

另外，Moments accountant：其跟踪隐私损失随机变量，概括了追踪(ε,δ)的传统方法和使用强组合理论直接从它组合可能导致结果是松的。我们转而计算隐私损失随机变量时刻的对数矩（log），这些是线性组合的。之后，使用the moment bound和马尔代夫不等式（Markov inequality）来获得尾部边界，那就是差分隐私上的隐私丢失。

隐私损失定义为：

而对于特定噪声分布下的隐私损失以及隐私损失的构成进行了大量的研究，产生最佳整体限制的结果是强组合理论，然而强组合理论可能是不准确的，无法将特殊噪声分布纳入考虑。文中所提方法相较于强组合理论，σ能节省。（目前理解是σ的节省，能带来更大的ε，隐私保护强度可以做到更高，所以文中的方法更有效）

此外，文中提出可以调节的超参数，从而平衡隐私、准确性和性能。发现对于神经网络模型结构的准确性对训练参数更敏感，比如batch的大小、噪声水平。而凸目标函数的差分隐私优化是使用小到1的批处理大小（batch size）来最佳实现的，非凸学习本身固有的稳定性较差，这受益于聚集成较大的Batch。当模型收敛到局部最优时，非差分隐私训练中的学习率通常会向下调整。而我们永远不需要把学习率降低到一个很小的值，因为从本质上讲，差分隐私训练永远不会达到一个需要被判断的领域。（另外，文中的定理1证明了batchsize过大会增加隐私成本）

具体实验有两个步骤：①sanitzer：对梯度预处理以保护隐私；②privacy-accountant：跟踪训练过程中的隐私成本。如下图6所示，强合成定理与文中方法的对比，证明文中方法需要的ε更低，即可提供更高的隐私保护。同时，如图7所示，文中实验比较了不同的ε和δ对准确率的影响。

 

图6 强合成定理与文中方法的比较

图7 不同的ε和δ对准确率的影响