求一个整数的划分

所谓整数拆分即把整数分解成若干整数的和（相当于把n个无区别的球放到n个无标志的盒子，盒子允许空，也允许放多于一个球）。
整数拆分成若干整数的和，办法不一，不同拆分法的总数叫做拆分数。

母函数法求一个整数的拆分：

 

#include <iostream>  //母函数法求一个整数的划分

using namespace std;

int c2[1000],c1[1000];

int main()

{

    int n;

    while(1)

    {

        cin>>n;

        int i,j,k;

        for(i=0;i<=n;i++)

        {

            c2[i]=0;

            c1[i]=1;

        }

        for(i=2;i<=n;i++)

        {

            for(j=0;j<=n;j++)

                for(k=0;j+k<=n;k+=i)

                c2[j+k]+=c1[j];

            for(j=0;j<=n;j++)

            {

                c1[j]=c2[j];

                c2[j]=0;

            }    

        }

        cout<<c1[n]<<endl;

    }

    

    return 0;

}

 递归法求整数拆分

解法 ：
在正整数n的所有不同划分中，将最大加数n1不大于m的化划分个数记为q(n,m);
(1) n>=1 q(n,1)=1 当最大加数n1不大于1时任何正整数n只有一种划分的形式。
(2) m>=n q(n,m)=q(n,n) 最大加数不能大于n
(3) m=n q(n,n)=1+q(n,n-1)正整数n的划分由n1=n的划分和n1≤n-1的划分组成。
(4) n>m>1 q(n,m)=q(n,m-1)+q(n-m,m);
正整数n的最大加数n1不大于m的划分由n1=m的划分和n1≤m-1 的划分组成
归纳如下：

 

 

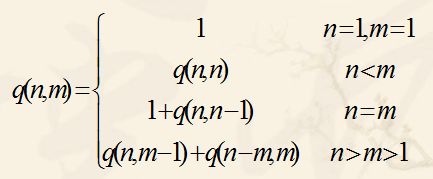
不过时间上要比母函数的时间长很多。

代码如下：

#include<iostream>//递归法求整数划分

using namespace std;

int q(int n,int m)

{

    if(n<1||m<1)return 0;

    if(n==1||m==1)return 1;

    if(n<m)return q(n,n);

    if(n==m)return 1+q(n,m-1);

    return q(n,m-1)+q(n-m,m);

}

int main()

{

    int n;

    while(1)

    {

    cin>>n;

    cout<<q(n,n)<<endl;

    }

    return 0;

}

建议用母函数法。