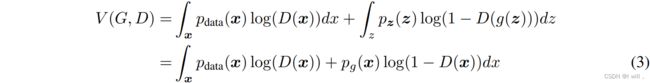Generative Adversarial Nets 论文翻译

论文原文：	https://dl.acm.org/doi/pdf/10.1145/3422622
代码：	GitHub - goodfeli/adversarial: Code and hyperparameters for the paper "Generative Adversarial Networks"

标记意义
test	个人的理解
test	不太懂的翻译
test	重点关注文本

目录

Generative Adversarial Nets

Abstract

1 Introduction

2 Related work

3 Adversarial nets

 4 Theoretical Results

4.1 pg = pdata 的全局最优性

 4.2 算法1的收敛

5 实验

6 优缺点

7 结论和未来工作

致谢

References

---

Generative Adversarial Nets

作者：Ian J. Goodfellow∗ , Jean Pouget-Abadiey , Mehdi Mirza, Bing Xu, David Warde-Farley,
Sherjil Ozairz , Aaron Courville, Yoshua Bengiox
Departement d’informatique et de recherche op ´ erationnelle ´
Universite de Montr ´ eal ´
Montreal, QC H3C 3J7

译者：I will，Sichuan University

Abstract

       我们提出了一个新的框架，通过一个对抗的过程来估计生成模型，其中我们同时训练两个模型:一个生成模型G 捕捉数据分布，以及一个判别模型D用来估计样本来自训练数据而不是来自G的概率【实际上，判别模型D就是尽可能让生成模型G犯错）】。这个框架相当于一个极大极小双人博弈游戏。在任意函数G和D的空间中，存在唯一解，其中G恢复训练数据分布，D处处等于1/2【这里的1/2现在看不懂没关系，文章会解释】。在G和D被定义的情况下，整个系统就可以通过多层感知器用反向传播来训练。在样本的训练或生成过程中，不需要任何马尔可夫链或展开的近似推理网络。实验通过对生成的样本进行定性和定量评估证明了该框架的潜力。

1 Introduction

       深度学习的前景是探究丰富的、有层次的模型，这种模型用来计算在人工智能应用程序中遇到的各种数据的概率分布。例如自然自然语言语料库中的图像、包含语音的音频波形和符号数据(简单介绍领域)。到目前为止，深度学习领域最成功的成果大都涉及辨别模型，辨别模型通常是将那些高维度、丰富的感官输入信息映射到类别标签的模型。这些惊人的成果主要是基于反向传播和dropout算法，使用了具有特别良好梯度的分段线性单位。深度生成模型的影响较小，这是由于难以逼近在最大似然估计和相关策略中出现的许多难以处理的概率计算，并且由于难以在生成环境中利用分段线性单元的优势(研究的现状，即优缺点)。我们提出了一个新的生成模型避开这些困难的估计程序(自己的工作)。

       在提出的对抗网络框架中，生成模型与判别模型进行对抗。判别模型用来学习确定样本是来自模型分布还是数据分布。生成模型可以被认为类似于一群造假者，他们试图制造假币并在不被发现的情况下使用它，而判别模型则类似于警察，试图检测假币。这个游戏中的竞争促使两个团队不断改进他们的方法，直到假货和正品无法区分为止【生成模型G胜利】。

       该框架可以为多种模型和优化算法提供特定的训练算法。在本文中，我们探讨了生成模型通过将随机噪声传递给多层感知器来生成样本的特殊情况，当然判别模型也是一个多层感知器。我们把这种特殊情况称为对抗网。在这种情况下，我们可以只使用非常成功的反向传播和dropout算法训练两个模型，并只使用前向传播从生成模型中取样。近似推论或马尔可夫链并不是必要的。

2 Related work

       暂时略过，写的是前人的工作

3 Adversarial nets

       当模型都是多层感知器时，对抗性建模框架最容易应用。为了了解生成器在数据x上的分布，我们定义了一个先验输入噪声变量，然后表示噪声变量到数据空间的映射，这个是一个可微函数，由参数为的多层感知器表示。我们还定义了第二个多层感知器来输出单个标量。表示来自真实数据而不是生成器输入变量的概率。我们训练D以最大化 将正确标签分配给训练样本和来自G的样本的概率【意思是，尽量让D可以分辨出某个样本是来自训练样本，还是来自于G生成的样本，来自训练样本时D(x)=1，来自生成样本时D(x)=0】。我们同时训练G最小化。换句话说，D和G使用值函数V(G,D)进行如下的二人极小极大博弈：

在下一节中，我们提出了对抗网络的理论分析，本质上表明，训练准则允许在G和D被给予足够的容量且没有参数限制时，恢复数据生成分布。请参见图1，以获得对该方法的不太正式、更具有教学意义的解释。在实践中，我们必须使用迭代的数值方法来实现游戏。在训练的内环中，优化D以完成在计算是被禁止的，并且在有限的数据集上将导致过拟合。相反，我们在交替进行k个优化D的步骤和1个优化G的步骤。这导致D保持在其最优解附近，只要G更新的足够缓慢。该过程在Algorithm 1中正式给出。

       在实际应用中，方程1可能无法提供足够的梯度让G学习得更好。在学习早期，当G较差时，D可以高置信度地拒绝样本，因为它们与训练数据明显不同。在这种情况下，饱和【恒为0】。那么，在学习早期，我们将训练G以最小化log(1 - D(G(z))更改为训练G以最大化log D(G(z))。这个目标函数导致G和D的动力学不动点相同，但是在学习早期提供更强的梯度。
 

 4 Theoretical Results

       生成器G隐式地定义一个概率分布作为样本的分布G(z) = z ~ pz。因此，如果有足够的容量和训练时间，我们希望算法1收敛到一个好的估计器。本节的结果是在没有限制的情况下完成的，例如，我们通过研究概率密度函数空间中的收敛性来表示一个具有无限容量的模型。我们将在4.1节中说明，这个极大极小博弈游戏，具有全局最优解对于 =。然后，我们将在4.2节中展示算法1优化Eq1，从而获得所期望的结果。

Figure 1: 生成式对抗网络被训练时，同时更新判别分布(D，蓝色，虚线)，以便区分来自数据生成分布(黑色，虚线)和生成分布 (G，绿色，实线)的样本。下面的水平线是 z 被采样的区域，在这种情况下是均匀的。上面的水平线是定义域 x 的一部分。向上的箭头表示映射x = G(z)如何对转换后的样本施加非均匀分布。在的高密度区域收缩，在的低密度区域膨胀。   (a) 考虑一个接近收敛的对抗对：和相似, 是一个部分准确的分类器。 (b) 在算法的内循环中训练D，从数据中区分样本，收敛到。 (c) G更新后，D的梯度引导G(z)流向更有可能被归类为数据的区域。 (d)经过几个步骤的训练，如果G和d有足够的能力，它们会达到一个都不能提高的点，因为= 。鉴别器无法区分两个分布，即D(x) = 1 / 2。

Algorithm 1 生成式对抗网络的小批量随机梯度下降训练。应用于鉴别器的步数k是一个超参数。我们在实验中使用k = 1，这是最便宜的选项。【k是一个超参数，适当的k应该使得G和D在进步过程中，进步程度相同。】

for 训练迭代次数 do         for k步骤 do                 (-) 来自于噪声先验的m个噪声样本的小批量样本。                 (-) 来自于数据生成分布G的m个样本的小批量样本。                 (-) 通过提升鉴别器的随机梯度来更新鉴别器:         end for         来自于噪声先验的m个噪声样本的小批量样本。         通过降低随机梯度来更新生成器: end for 基于梯度的更新可以使用任何标准的基于梯度的学习规则。我们在实验中使用了动量。

4.1 pg = pdata 的全局最优性

我们首先考虑任意给定发生器G的最佳鉴别器D。

命题1. 当G固定时，最佳鉴别器D为：

证明： 对于任何生成器G，判别器D的训练准则是使最大。

       对于任何，函数【这个函数是一个凸函数，存在最大值。其中，D(x)=1-y】在[0,1]内取到的最大值都是【可以对上面函数两边对y求导，导数=0求出】。鉴别器不需要定义在外部，也不需要在外部被证明。
      注意，D的训练目标可以解释为最大化对数似然函数，这个似然函数是用于估计条件概率的，其中Y表示x是否来自(y = 1)或从 (y = 0)。方程1中的极大极小博弈现在可以重新表述为:

定理1：当且仅当pg = pdata时，实现了虚拟训练准则C(G)的全局最小值。此时C(G)的值最小且为−log 4。
证明：对于pg = pdata时, (考虑式2)。因此，通过将带入公式4，我们发现C(G) = log (1/2) + log (1/2) = −log 4。要看到这是C(G)的最佳可能值，仅在pg = pdata时达到，请观察下式：

补充一个知识点先：【KL散度：log(p/g)用来衡量两个分布p和g的相似度。为了使上式中Pdata(x) + Pg(x)的期望为1，即是一个分布，写为下式，这样就构造出了KL散度】

那么，从中减去-log4后，我们得到C(G)的新表达式【含KL散度】：

其中KL是Kullback-Leibler散度。我们在前面的表达式中认识到模型分布与数据生成过程之间的詹森香农散度:

由于两个分布之间的Jensen-Shannon散度总是非负的，如果两个分布相等则散度为零，我们证明了 是C(G)的全局最小值。唯一的解是pg = pdata，即生成模型完美地复制了数据分布。
 

 4.2 算法1的收敛

       命题2：如果G和D有足够的容量，并且在算法1的每一步，都允许鉴别器在给定生成器G的情况下达到最优，并更新pg，以改进下面的标准：

然后，pg逐渐收敛到pdata。

       证明：正如上述准则所做的那样，考虑V(G;D) = U(pg;D)作为pg的函数。注意U(pg;D) 在函数空间pg上是凸函数。凸函数的极值的子导数包括该函数在得到极值处的导数。换句话说，如果【sup在数学上表示求最小上界，一个极值】，并且对于每一个α在x上是凸的，那么在时，有。这相当于在给定相应G的最佳D下，去通过梯度下降来更新pg。在pg中是凸的，具有唯一的全局最优值，如thm1所证明的，因此pg更新足够小，pg会收敛到px，证明结束。

        在实践中，对抗网通过函数G(z;θg)代表pg发行版的有限系列，敌对网络通过函数G(z；θg)，并且我们优化了θg而不是pg本身，所以证明并不适用。然而，多层感知器在实践中的出色表现表明，尽管缺乏理论保证，但它们是一个合理的模型。

表1: 基于Parzen窗口的对数似然估计。MNIST报告的数字是测试集上样本的平均对数似然，是用跨实例计算的平均值的标准误差。在TFD上，我们计算了数据集的多个折叠的标准误差，使用每个折叠的验证集选择不同的σ。在TFD上，对每条折叠数据集进行交叉验证，并计算每条折叠的平均对数似然。对于MNIST，我们将其与数据集的实值(而不是二进制)版本的其他模型进行比较。

5 实验

        我们用一系列数据集训练对抗网络，包括MNIST[21]，多伦多人脸数据库(TFD) [27]， CIFAR-10[19]。生成网络使用修正的线性激活函数和[17，8]和sigmoid激活混合激活，而鉴别器网络使用maxout[9]激活函数。采用Dropout[16]训练鉴别器网络。虽然我们的理论框架允许在生成器的中间层使用dropout和其他噪声，但我们只使用噪声作为生成器网络最底层的输入。

       我们通过将高斯Parzen窗口拟合到G生成的样本中，估计了pg下测试集数据的概率，并且报告这个分布下的对数似然。在验证集上进行交叉验证，得到高斯函数的σ参数。该过程在Breuleux等人的[7]中被引入，并用于各种确切似然是不可处理的生成模型[24,3,4]。结果如表1所示。这种估计可能性的方法方差有点大，并且它在高维空间中表现不佳但它是我们所知的最好的方法。生成模型的进步可以尝试，但不能估计将来研究的可能性，比如激励进一步研究如何评估这些模型。在图2和图3中，我们展示了训练后从生成器网络中提取的样本。虽然我们并没有声称这些样本比现有方法生成的样本更好，但我们相信这些样本至少与文献中最好的生成模型具有竞争力，并突出了对抗框架的潜力。
 

6 优缺点

       这个新框架相对于以前的建模框架有优点也有缺点。缺点主要是没有显式表示pg(x)，并且D在训练时必须与G很好地同步（特别是G在没有更新D的情况下一定不能训练太多，以避免“Helvetica场景”，这时G会将太多的z值映射到相同的x值，从而有足够的多样性来建模pdata），就像玻尔兹曼机器的负链必须在学习步骤之间保持更新一样。优点是不需要马尔可夫链，只使用backprop来获得梯度，在学习过程中不需要推理，并且可以将各种各样的函数纳入模型。表2总结了生成对抗网络与其他生成建模方法的比较。

       前面提到的优势主要是计算方面的。对抗模型也可能获得一些统计优势，因为生成器网络不直接使用数据示例更新，而只使用流经鉴别器的梯度。这意味着输入的组件不会直接复制到生成器的参数中。对抗网络的另一个优点是，它们可以表示非常尖锐，甚至退化的分布。而基于马尔可夫链的方法要求分布具有模糊性，以便链能够在模式之间混合。

7 结论和未来工作

       这个框架允许许多简单的扩展：

图2: 模型样本的可视化。最右边一列显示了邻近样本中最近的训练示例，以证明模型没有记住训练集。样本是随机抽取的，不是精心挑选的。与大多数其他深度生成模型的可视化不同，这些图像显示了来自模型分布的实际样本，而不是给定隐藏单元的条件样本。此外，这些样本是不相关的，因为采样过程不依赖于马尔可夫链混合。a) MNIST；b) TFD；c) CIFAR-10(全连接模型)；d) CIFAR-10(卷积判别器和“反卷积”生成器)

图3：全模型z空间坐标间线性插值得到的数字

       1. 通过在G和D中添加c作为输入，可以得到一个条件生成模型 p(x / c)
       2. 学习的近似推理可以通过训练辅助网络来预测给定x的z。这类似于清醒-睡眠算法[15]训练的
           推理网络，但优点是在生成网络训练完成后，推理网络可以训练为特定的生成网络。
       3. 我们可以对所有条件进行近似建模，其中S是x指标的子集，方法是训练一组共享
           参数的条件模型。
       4. 半监督学习:来自鉴别器或推断网的特征可以在有限的标记数据可用时提高分类器的性能。
       5. 效率提高:通过设计更好的方法来协调G和D，或者在训练期间确定更好的样本z分布，可以
           大大加速训练。
       本文证明了对抗建模框架的可行性，表明这些研究方向可能是有用的。

	深度有向图形模型	深度无向图形模型	生成式自动编码器	对抗模型
训练	训练期间需要的推理	培训期间需要推理。 MCMC需要近似配分函数梯度。	混合和重建生成器之间的强制权衡	使鉴别器与生成器同步。Helvetica.
推理	学习的近似推理	变分推理	基于MCMC的推理	学习的近似推理
采样	没有困难	需要马尔科夫链	需要马尔科夫链	没有困难
评价 p(x)	棘手，可以近似于AIS	棘手，可以近似于AIS	不能明确表示，可近似用帕岑密度估计	不能明确表示，可近似用帕岑密度估计
模型设计	模型需要设计成与期望的推断方案一起工作-一些推理方案支持类似GANs的模型族	精心的设计需要确保多种属性	任何可微函数理论上都是允许的	任何可微函数理论上都是允许的
表2：生成式建模中的挑战：对涉及模型的每个主要操作的不同深度生成建模方法所遇到的困难的总结。

致谢

       我们要感谢Patrice Marcotte, Olivier Delalleau, Kyunghyun Cho, Guillaume、Alain 和 Jason Yosinski进行有益的讨论。Yann Dauphin与我们分享了他的Parzen窗口计算代码。我们要感谢Pylearn2[11]和Theano[6,1]的开发人员，特别是Fred´eric Bastien，他为这个项目特别推出了Theano特性。Araud Bergeron在LATEX排版方面提供了急需的支持。我们也要感谢CIFAR，加拿大研究主席提供资金，加拿大计算中心和魁北克计算中心提供计算资源。伊恩·古德费罗获得2013年谷歌奖学金的支持深度学习。最后，我们要感谢《三个铜手》激发了我们的创造力。

References

1. Bastien, F., Lamblin, P., Pascanu, R., Bergstra, J., Goodfellow, I. J., Bergeron, A., Bouchard,   N., and Bengio, Y. (2012). Theano: new features and speed improvements. Deep Learning and Unsupervised Feature Learning NIPS 2012 Workshop.
2. Bengio, Y. (2009). Learning deep architectures for AI. Now Publishers.
3. Bengio, Y., Mesnil, G., Dauphin, Y., and Rifai, S. (2013). Better mixing via deep representations. In ICML’13.
4. Bengio, Y., Thibodeau-Laufer, E., and Yosinski, J. (2014a). Deep generative stochastic networks trainableby backprop. In ICML’14.
5. Bengio, Y., Thibodeau-Laufer, E., Alain, G., and Yosinski, J. (2014b). Deep generative stochastic networks trainable by backprop. In Proceedings of the 30th International Conference on Machine Learning(ICML’14).
6. Bergstra, J., Breuleux, O., Bastien, F., Lamblin, P., Pascanu, R., Desjardins, G., Turian, J., Warde-Farley,D., and Bengio, Y. (2010). Theano: a CPU and GPU math expression compiler. In Proceedings of the Python for Scientific Computing Conference (SciPy). Oral Presentation.
7. Breuleux, O., Bengio, Y., and Vincent, P. (2011). Quickly generating representative samples from an RBM-derived process. Neural Computation, 23(8), 2053–2073.
8. Glorot, X., Bordes, A., and Bengio, Y. (2011). Deep sparse rectifier neural networks. In AISTATS’2011.8
9. Goodfellow, I. J., Warde-Farley, D., Mirza, M., Courville, A., and Bengio, Y. (2013a). Maxout networks.In ICML’2013.
10. Goodfellow, I. J., Mirza, M., Courville, A., and Bengio, Y. (2013b). Multi-prediction deep Boltzmann machines. In NIPS’2013.
11. Goodfellow, I. J., Warde-Farley, D., Lamblin, P., Dumoulin, V., Mirza, M., Pascanu, R., Bergstra,J., Bastien, F., and Bengio, Y. (2013c). Pylearn2: a machine learning research library. arXiv preprint arXiv:1308.4214.
12. Gregor, K., Danihelka, I., Mnih, A., Blundell, C., and Wierstra, D. (2014). Deep autoregressive networks. In ICML’2014.
13. Gutmann, M. and Hyvarinen, A. (2010). Noise-contrastive estimation: A new estimation principle for unnormalized statistical models. In Proceedings of The Thirteenth International Conference on Artificial Intelligence and Statistics (AISTATS’10).
14. Hinton, G., Deng, L., Dahl, G. E., Mohamed, A., Jaitly, N., Senior, A., Vanhoucke, V., Nguyen, P.,Sainath, T., and Kingsbury, B. (2012a). Deep neural networks for acoustic modeling in speech recognition.IEEE Signal Processing Magazine, 29(6), 82–97.
15. Hinton, G. E., Dayan, P., Frey, B. J., and Neal, R. M. (1995). The wake-sleep algorithm for unsupervised neural networks. Science, 268, 1558–1161.
16. Hinton, G. E., Srivastava, N., Krizhevsky, A., Sutskever, I., and Salakhutdinov, R. (2012b). Improving neural networks by preventing co-adaptation of feature detectors. Technical report, arXiv:1207.0580.
17. Jarrett, K., Kavukcuoglu, K., Ranzato, M., and LeCun, Y. (2009). What is the best multi-stage architecture for object recognition? In Proc. International Conference on Computer Vision (ICCV’09), pages 2146–2153.IEEE.
18. Kingma, D. P. and Welling, M. (2014). Auto-encoding variational bayes. In Proceedings of the International Conference on Learning Representations (ICLR).
19. Krizhevsky, A. and Hinton, G. (2009). Learning multiple layers of features from tiny images. Technical report, University of Toronto.
20. Krizhevsky, A., Sutskever, I., and Hinton, G. (2012). ImageNet classification with deep convolutional neural networks. In NIPS’2012.
21. LeCun, Y., Bottou, L., Bengio, Y., and Haffner, P. (1998). Gradient-based learning applied to document recognition. Proceedings of the IEEE, 86(11), 2278–2324.
22. Mnih, A. and Gregor, K. (2014). Neural variational inference and learning in belief networks. Technical report, arXiv preprint arXiv:1402.0030.
23. Rezende, D. J., Mohamed, S., and Wierstra, D. (2014). Stochastic backpropagation and approximate inference in deep generative models. Technical report, arXiv:1401.4082.
24. Rifai, S., Bengio, Y., Dauphin, Y., and Vincent, P. (2012). A generative process for sampling contractive auto-encoders. In ICML’12.
25. Salakhutdinov, R. and Hinton, G. E. (2009). Deep Boltzmann machines. In AISTATS’2009, pages 448–455.
26. Schmidhuber, J. (1992). Learning factorial codes by predictability minimization. Neural Computation,4(6), 863–879.
27. Susskind, J., Anderson, A., and Hinton, G. E. (2010). The Toronto face dataset. Technical Report UTMLTR 2010-001, U. Toronto.
28. Szegedy, C., Zaremba, W., Sutskever, I., Bruna, J., Erhan, D., Goodfellow, I. J., and Fergus, R. (2014).Intriguing properties of neural networks. ICLR, abs/1312.6199.
29. Tu, Z. (2007). Learning generative models via discriminative approaches. In Computer Vision and Pattern Recognition, 2007. CVPR’07. IEEE Conference on, pages 1–8. IEEE.