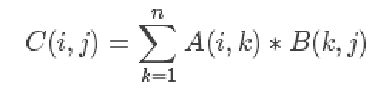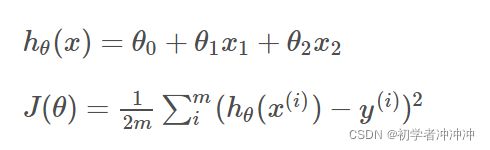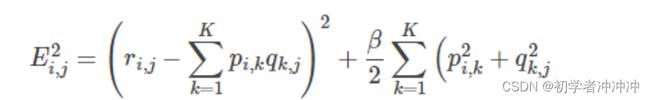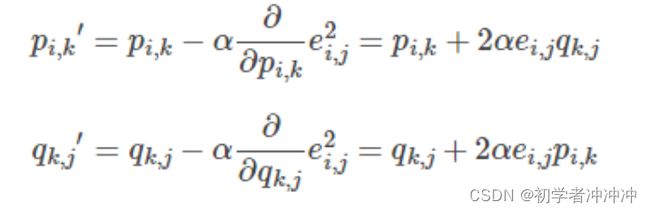矩阵分解与梯度下降 1月九日学习笔记

1.矩阵的乘法与分解

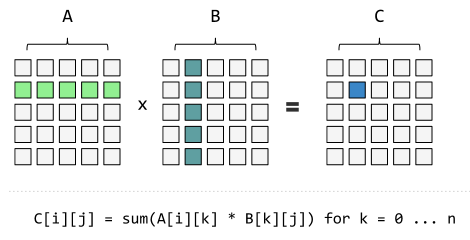
矩阵乘法的原理示意图：

矩阵乘法的公式：

矩阵乘法的具体例子：

同样的利用矩阵的乘法的原理我们同样可以一个矩阵分解为两个矩阵。

 例如一个4*5的矩阵可以分解为一个4*K与K*5的矩阵。

2.损失函数：

损失函数用来评价模型的预测值和真实值不一样的程度，损失函数越小，通常模型的性能越好。不同的模型用的损失函数一般也不一样

通俗来讲就是，用数据的真实值去减去采用函数模型得到的预测值，计算的是一个样本的误差。它是用来估量你模型的预测值 f(x)与真实值 Y的不一致程度。 

公式为 LOSS=真实值-预测值

我们当前主要常用的是：均方差损失函数

采用矩阵形式的损失函数：

我们构造好了损失函数，自然希望能够得到一个是误差尽可能小的 函数模型，也就是找到这个损失函数取最小值时的参数，而方法就用到梯度下降的方法来得到目标函数。 

3.梯度下降与偏导：

 梯度下降（gradient descent）在机器学习中应用十分的广泛，不论是在线性回归还是Logistic回归中，它的主要目的是通过迭代找到目标函数的最小值，或者收敛到最小值。

   3.1偏导：

在一元函数中，导数就是函数的变化率。对于二元函数的“变化率”，由于自变量多了一个，情况就要复杂的多。

在 xOy 平面内，当动点由 P(x0,y0) 沿不同方向变化时，函数 f(x,y) 的变化快慢一般来说是不同的，因此就需要研究 f(x,y) 在 (x0,y0) 点处沿不同方向的变化率。

在这里我们只学习函数 f(x,y) 沿着平行于 x 轴和平行于 y 轴两个特殊方位变动时， f(x,y) 的变化率。

偏导数的表示符号为:∂。偏导数反映的是函数沿各个坐标轴正方向的变化率。梯度的最大方向就是方向导数方向也就是数值变化最快的方向。

3.2梯度下降；

我们可以用下山作为例子：（这里引用别人所举出的例子）

假设这样一个场景：一个人被困在山上，需要从山上下来(找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低；因此，下山的路径就无法确定，必须利用自己周围的信息一步一步地找到下山的路。这个时候，便可利用梯度下降算法来帮助自己下山。怎么做呢，首先以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前位置为基准，再找最陡峭的地方，再走直到最后到达最低处；

总之：通俗来讲就是利用当前位置的信息，一步一步迭代，找到最小值所在位置。

通过我们所学的高数知识知道，沿导数方向就是数值变化的最大方向。所以求导是必不可少的，就如同下山一样，我们有了下山方向就要考虑自己的下山所迈出的步伐，步长也是梯度下降中的一个重要参数，有了下山的方向也有了自己下山的步长，我们就可以一步一步进行一直到山底，也就是我们想要求出的函数中最小值点的参数。

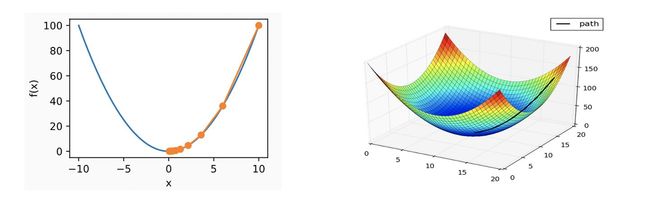
下面是一维以及多维的示意图：。

参数更新的主要步骤：

1.随机初始化一组参数θ

2.将目标函数J(θ)J(θ)分别对每个参数θ求偏导，（也可以理解为每个当前位置下山的最快方向）

3.用旧的值减去旧的值的导数乘于步长得到新的值。

θnew=θold-a *f'（θold）

a 为学习效率（也可以理解为下山的步伐）

b为每次迭代X的变化量  b=θold-θnew。

4.迭代次数一般通过2个参数控制

         初设的循环次数  或者 当b 也就是变化量小于一个特定的值。注意：a可以自己设定不易过大或过小，过大容易造成不准确，过小容易造成迭代次数过多。

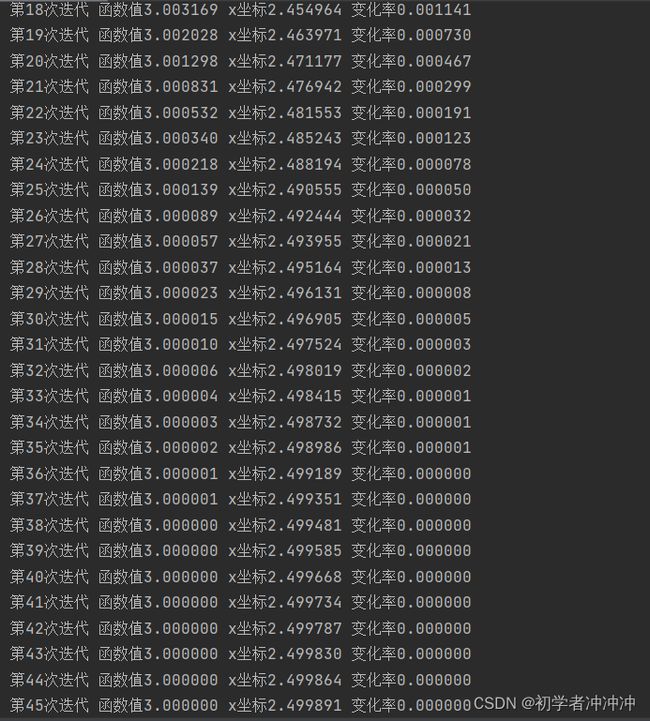
 下面看一个具体例子：（利用梯度下降求损失函数最小值点参数）

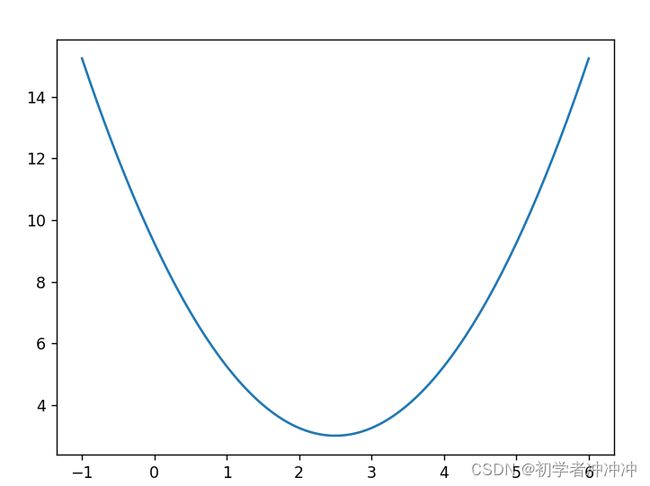
另一个y=(x-2.5)**2+3为例：（求函数最小值点对应的横坐标）

 

 

 可以看到所求梯度下降得到最低点已经十分逼近函数真实最低点2.5了

部分代码实现

def dJ(x):
    return 2*(x-2.5)

###定义一个求函数值的函数J
def J(x):
    try:
        return (x-2.5)**2+3
    except:
        return float('inf')
x=0.0							#随机选取一个起始点
eta=0.1		#学习率
i=0
epsilon=1e-8				    #用来判断是否到达二次函数的最小值点的条件
history_x=[x]                   #用来记录使用梯度下降法走过的点的X坐标
while True:
    i=i+1
    d=(x-2.5)**2+3
    gradient=dJ(x)				#梯度（导数）
    last_x=x
    x=x-eta*gradient
    print("第%d次迭代 函数值%f x坐标%f 变化率%f"%(i,J(last_x),x,abs(J(last_x)-J(x))))
    history_x.append(x)
    if (abs(J(last_x)-J(x)) 

 4.正则化：（这个也不太明白）

 我们一般为了防止过拟合，在损失函数中增加正则化项

以矩阵为例：

也即是：

 有了上面的基础知识我们来看看关于矩阵分解的例子

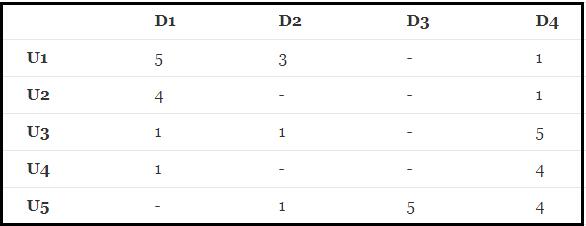
 我们可以看U代表user及也就是用户，D表示数据也就是data（代表评分）。

图中有未评分的项目，我们要利用其他数据来预估这些评分。

 首先我们可以将矩阵拆分为2个矩阵的相乘。

R（m,n）为原始矩阵，Q（m,k）和P(k,n)为分解矩阵。

此时R1=Q*P。R1为预估矩阵。使R近似等于R1

1.我们要构建损失函数：

 2.对其求偏导：

 3.更新参数：

 4.接下来就是不断的迭代了。（一般要加入正则化这里也不要太明白就不加了）

下面是借鉴的别人的代码（自己初学还写不出来），看一下利用python的代码实现

# from pylab import *
import matplotlib.pyplot as plt
from math import pow
import numpy


def matrix_factorization(R,P,Q,K,steps=5000,alpha=0.0002,beta=0.02):
    Q=Q.T  # .T操作表示矩阵的转置
    result=[]
    for step in range(steps):
        for i in range(len(R)):
            for j in range(len(R[i])):
                if R[i][j]>0:
                    eij=R[i][j]-numpy.dot(P[i,:],Q[:,j]) # .dot(P,Q) 表示矩阵内积
                    for k in range(K):
                        P[i][k]=P[i][k]+alpha*(2*eij*Q[k][j]-beta*P[i][k])
                        Q[k][j]=Q[k][j]+alpha*(2*eij*P[i][k]-beta*Q[k][j])
        eR=numpy.dot(P,Q)
        e=0
        for i in range(len(R)):
            for j in range(len(R[i])):
                if R[i][j]>0:
                    e=e+pow(R[i][j]-numpy.dot(P[i,:],Q[:,j]),2)
                    for k in range(K):
                        e=e+(beta/2)*(pow(P[i][k],2)+pow(Q[k][j],2))
        result.append(e)
        if e<0.001:
            break
    return P,Q.T,result

if __name__ == '__main__':
    R=[
        [5,3,0,1],
        [4,0,0,1],
        [1,1,0,5],
        [1,0,0,4],
        [0,1,5,4]
    ]

    R=numpy.array(R)

    N=len(R)
    M=len(R[0])
    K=2

    P=numpy.random.rand(N,K) #随机生成一个 N行 K列的矩阵
    Q=numpy.random.rand(M,K) #随机生成一个 M行 K列的矩阵

    nP,nQ,result=matrix_factorization(R,P,Q,K)
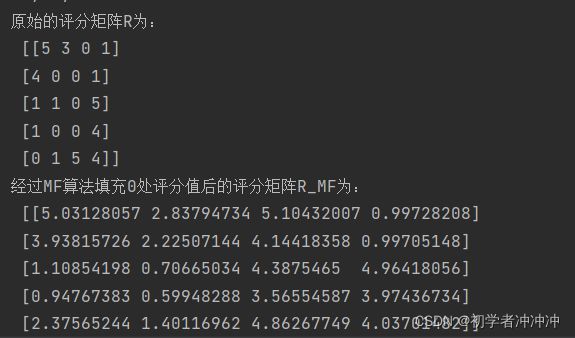
    print("原始的评分矩阵R为：\n",R)
    R_MF=numpy.dot(nP,nQ.T)
    print("经过MF算法填充0处评分值后的评分矩阵R_MF为：\n",R_MF)

 5总结：

主要学习矩阵的乘法与分解，以及什么是损失函数，然后就是利用梯度下降法去求得损失函数的最小值，这里也要清楚高等数学中的偏导概念，最后一般防止过度拟合要加入正则化（这个目前自己还不是特别清楚），其中还加了一些pytohn代码的实现，自己确实有很多地方不太清楚，刚开始写这些，也借鉴了许多别人的文章，那些人文章写的非常好，自己以后也会进步的。