知识图谱学习笔记(二)——机器学习基础
机器学习基础
1. 机器学习基础理论与概念
1.1 机器学习概要
机器学习专门研究计算机怎样模拟或实现人类的学习行为,以获取新的知识或技能,重新组织已有的知识结构使之不断改善自身的性能。它是人工智能的核心,是使计算机具有智能的根本途径,其应用遍及人工智能的各个领域,它主要使用归纳、综合而不是演绎。
机器学习主要是研究如何使计算机从给定的数据中学习规律,从观测数据(样本)中寻找规律,并利用学习到的规律(模型)对未知或无法观测的数据进行预测。
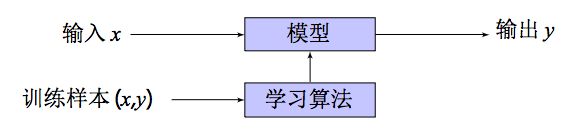
训练数据: ( x i , y i ) , 1 ≤ i ≤ m (x_i, y_i), 1 \leq i \leq m (xi,yi),1≤i≤m
模型:
线 性 方 法 : y = f ( x ) = w T x + b 线性方法:y = f(x) = w^Tx + b 线性方法:y=f(x)=wTx+b
非 线 性 方 法 : 神 经 网 络 非线性方法:神经网络 非线性方法:神经网络
优化:
损 失 函 数 : L ( y , f ( x ) ) 损失函数:L(y, f(x)) 损失函数:L(y,f(x))
经 验 风 险 最 小 化 : Q ( θ ) = 1 m ∑ i = 1 m L ( y i , f ( x i , θ ) ) 经验风险最小化:Q(\theta) = \frac{1}{m}\sum_{i=1}^mL(y_i, f(x_i, \theta)) 经验风险最小化:Q(θ)=m1i=1∑mL(yi,f(xi,θ))
正 则 化 : ∣ ∣ θ ∣ ∣ 2 正则化:||\theta||^2 正则化:∣∣θ∣∣2
优化目标函数:
Q ( θ ) + λ ∣ ∣ θ ∣ ∣ 2 Q(\theta) + \lambda||\theta||^2 Q(θ)+λ∣∣θ∣∣2
1.2 机器学习问题类型
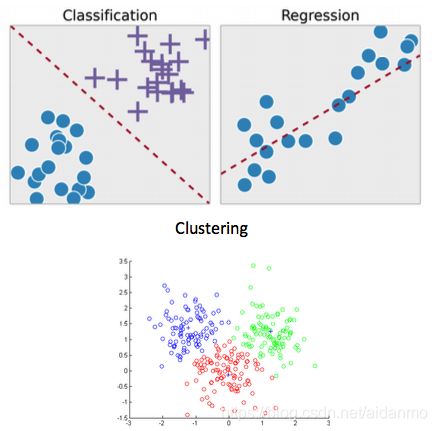
- 回归(Regression):y是连续值, f ( x ) f(x) f(x)的输出也是连续值。这种类型的问题就是回归问题。对于所有已知或未知的(x, y),使得 f ( x , θ ) f(x, \theta) f(x,θ)和y尽可能地一致。损函数通常定义为平方误差。
- 分类(Classification):y是离散的类别标记(符号),就是分类问题。损失函数一般用0-1损失函数或负对数似然函数等。在分类问题中,通过学习得到的决策函数 f ( x , θ ) f(x,\theta) f(x,θ)也叫分类器。
1.3 机器学习算法类型
- 有监督学习:利用一组已知输入x和输出y的数据来学习模型的参数,使得模型预测的输出标记和真实标记尽可能一致。
- 半监督学习:利用少量已知输入x和输出y的数据以及未标注的样本,来学习模型的参数。
- 无监督学习:用来学习的数据不包含标注信息,需要学习算法自动学习到一些有价值的信息,例如聚类(clustering)
2. 深度学习和神经网络基础
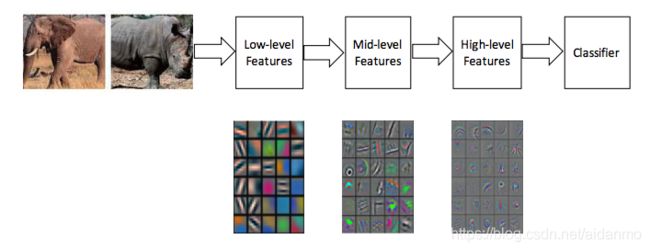
传统的机器学习:人工特征工程+分类器

深度学习:自动学习多尺度的特征表示
2.1 感知机 Perceptron
感知机是对生物神经细胞的简单数学模拟,是最简单的人工神经网络,只有一个神经元。
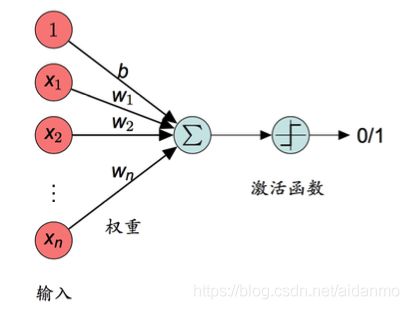
o u t p u t = { 0 i f ∑ j w j x j ≤ t h r e s h o l d 1 i f ∑ j w j x j < t h r e s h o l d output= \left\{ \begin{matrix} 0 & if \sum_j w_j x_j \leq threshold\\ 1 & if \sum_j w_j x_j < threshold\\ \end{matrix} \right. output={01if∑jwjxj≤thresholdif∑jwjxj<threshold
感知机参数学习:
L ( w , b ) = 1 2 ∑ x i ϵ M ( y i − ( w x i + b ) ) 2 y i ~ = w x i + b L(w, b) = \frac{1}{2} \sum_{x_i \epsilon M}{(y_i - (wx_i + b))^2} \quad\quad\quad \widetilde{y_i} = wx_i + b L(w,b)=21xiϵM∑(yi−(wxi+b))2yi =wxi+b
∂ L ( w , b ) ∂ w = − ∑ x i ϵ M ( y i − y i ~ ) x i ∂ L ( w , b ) ∂ b = − ∑ x i ϵ M ( y i − y i ~ ) \frac{\partial L(w, b)}{\partial w} = - \sum_{x_i \epsilon M}{(y_i - \widetilde{y_i})x_i}\quad\quad\quad \frac{\partial L(w, b)}{\partial b} = - \sum_{x_i \epsilon M}{(y_i - \widetilde{y_i})} ∂w∂L(w,b)=−xiϵM∑(yi−yi )xi∂b∂L(w,b)=−xiϵM∑(yi−yi )
w ← w + λ ∑ x i ϵ M ( y i − y i ~ ) x i b ← b + λ ∑ x i ϵ M ( y i − y i ~ ) w \leftarrow w + \lambda \sum_{x_i \epsilon M}{(y_i - \widetilde{y_i})x_i}\quad\quad\quad b \leftarrow b + \lambda \sum_{x_i \epsilon M}{(y_i - \widetilde{y_i})} w←w+λxiϵM∑(yi−yi )xib←b+λxiϵM∑(yi−yi )
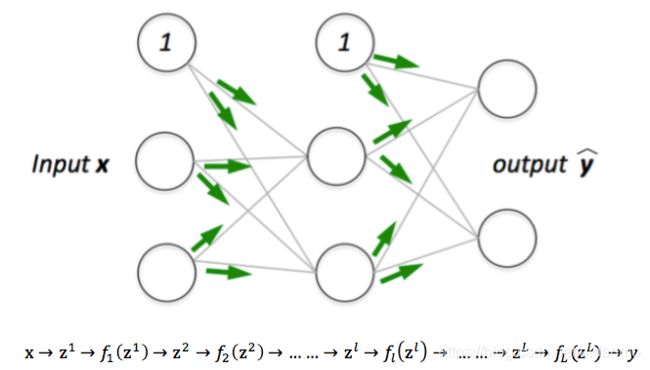
2.2 前馈神经网络 Feed Forward Neural Networks
- L 表 示 神 经 网 络 的 层 数 L表示神经网络的层数 L表示神经网络的层数
- n l 表 示 第 l 层 神 经 元 的 个 数 n^l表示第l层神经元的个数 nl表示第l层神经元的个数
- f l ( z ) 表 示 第 l 层 的 激 活 函 数 f_l(z)表示第l层的激活函数 fl(z)表示第l层的激活函数
- w l 表 示 第 l 层 的 权 重 w^l表示第l层的权重 wl表示第l层的权重
- b l 表 示 第 l 层 神 经 元 的 偏 置 b^l表示第l层神经元的偏置 bl表示第l层神经元的偏置
- z l 表 示 第 l 层 神 经 元 的 状 态 z^l表示第l层神经元的状态 zl表示第l层神经元的状态
- y l 表 示 第 l 层 神 经 元 的 输 出 y^l表示第l层神经元的输出 yl表示第l层神经元的输出
z l = w l y l − 1 + b l z^l = w^l y^{l-1} + b^l zl=wlyl−1+bl
y l = f l ( z l ) y^l = f_l(z^l) yl=fl(zl)
z l = w l f l ( z l − 1 ) + b l z^l = w^l f_l(z^{l-1}) + b^l zl=wlfl(zl−1)+bl
2.3 卷积神经网络 Convolutional Neural Network
卷积神经网络是一种前馈神经网络。局部链接,权值共享,采样。具有平移、缩放和扭曲不变形的特点。
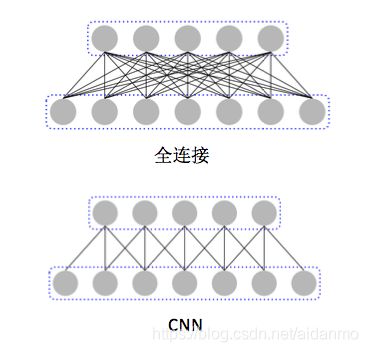
全连接存在的问题:权重矩阵参数非常多,训练效率低下。数据不足时,欠学习。
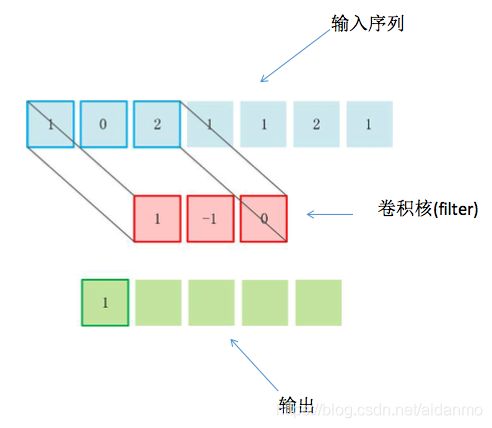
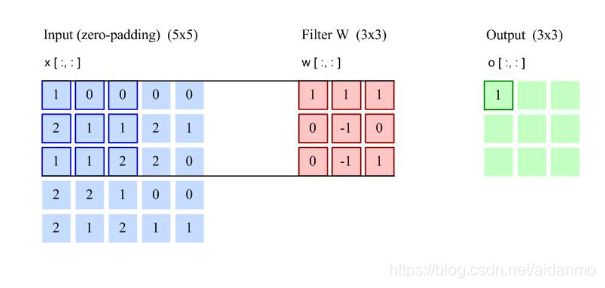
为了增强卷几层的表示能力,可以使用K个不同的滤波器来得到K组输出。每一组输出都共享一个滤波器。如果我们把滤波器看成一个特征提取器,每一组输出都可以看成是输入图像经过一个特征抽取后得到的特征。因此,在卷积神经网络中每一组输出也叫做一组特征映射。
关于CNN的具体讲解,推荐学习一下这篇博文一文让你彻底了解卷积神经网络里面的基础知识讲解的还是蛮细致的,就是反向传播的过程讲的有些突兀。
下面通过一个例子来了解一下CNN在图像处理中的应用。
LeNet-5提出时间比较早,是一个非常成功的神经网络模型。基于LeNet-5的手写数字识别系统在90年代被美国很多银行使用。该网络一共有7层。
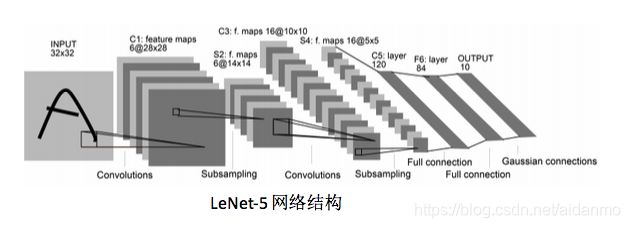
- 输入层:输入图像大小为32 X 32 = 1024.
- C1层:这一层是卷积层。滤波器的大小是55=25,共有6个滤波器,不使用全0填充,步长为1。得到6组大小为2828=784的特征映射。因此,C1层的神经元个数为6784=4704.可训练参数个数为625+6=156(其中包括6个偏置bias)。连接数为156*784=122304。
- S2层:这一层为子采样层,也称为池化层。由C1层每组特征映射中的22邻域点次采样为1个点(4个数的平均值),长和宽的步长均为2,所以本层的输出矩阵大小为1414*6。
- C3层:这一层为卷积层。使用16组,共60个滤波器,打下为55=25。滤波器与S2层特征的映射连接关系如下表所示:
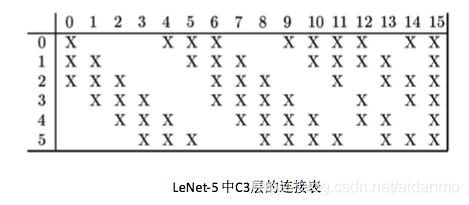
本层不使用全0填充,步长为1,得到16组大小为1010=100的特征映射,输出矩阵为161010。可训练参数个数为6025+16 = 1516。连接数为1516100 = 151600。 - S4层:这一层是子采样层,由22邻域点次采样为1个点,步长为2.本层的输出矩阵大小为55*16。
- C5层:这是一个卷积层,得到120组大小为11的特征映射。每个特征映射与S4层的全部特征映射相连。有12016=1920个滤波器,大小为55=25,C5层的神经元个数为120,可训练参数个数为192025+120=48120。
- F6层:全连接层,有84个神经元,可训练参数个数为84*(120+1)=10164个。
- 输出层:全连接层,输出层由10个欧式径向基函数组成。
2.4 循环神经网络 Recurrent Neural Network
前馈神经网络和CNN存在如下问题:
1.连接存在于层与层之间,每层的节点之间是无连接的。
2.输入和输出的维数是固定的,不能任意改变。无法处理变长的序列数据。
3.假设每次输入都是独立的,也就是说每次网络的输出只依赖于当前的输入。
循环神经网络通过使用自带反馈的神经元,能够处理任意长度的序列。
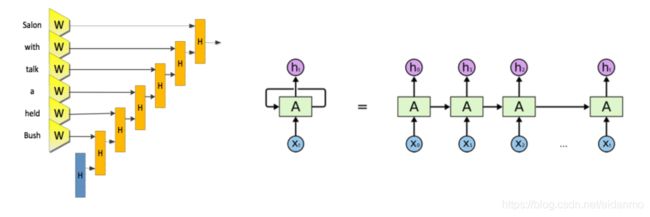
循环神经网络一个非常重要的概念就是时刻。其会对每一个时刻的输入结合当前模型的状态给出一个输出。
在RNN中,每一个时刻会有一个输入 X t X_t Xt,然后根据RNN当前的状态 A t A_t At提供一个输出 h t h_t ht。而RNN当前的状态 A t A_t At是根据上一个时刻的状态 A t − 1 A_{t-1} At−1和当前的输入 X t X_t Xt共同决定的。RNN最擅长解决的问题是与时间序列相关的。RNN要求每一个时刻都有一个输入,但是不一定每个时刻都需要有输出。
更直观的,我们可以得到如下图所示的循环神经网络:
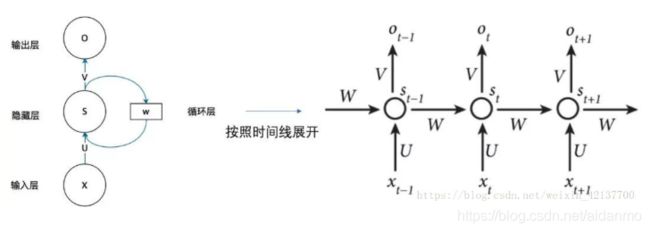
RNN包括了输入层、隐藏层和输出层。假设时刻t时,输入为 x t x_t xt,隐层状态为 s t s_t st。 s t s_t st不仅和当前时刻的输入相关,也喝上一个时刻的隐层状态 s t − 1 s_{t-1} st−1相关。一般可以使用如下函数:
s t = f ( W s t − 1 + U x t + b ) s_t = f(Ws_{t-1} + Ux_t + b) st=f(Wst−1+Uxt+b)
o t = s o f t m a x ( V s t ) o_t = softmax(Vs_t) ot=softmax(Vst)
这里, f f f是非线性函数,可以为sigmod函数或者tanh函数。
长短时记忆神经网络:LSTM :Long Short-Term Memory Neural Network
LSTM是RNN的一个变体,可以有效解决简单循环神经网络的梯度爆炸或消失问题。LSTM的关键是引入了一组记忆单元,允许网络可以学习何时遗忘历史信息,何时用新信息更新记忆单元。在时刻t时,记忆单元 c t c_t ct记录了当前时刻为止的所有历史信息,并受三个“门”控制:输入门 i t i_t it,遗忘门 f t f_t ft和输出门 o t o_t ot。三个门的元素的值在[0,1]之间。
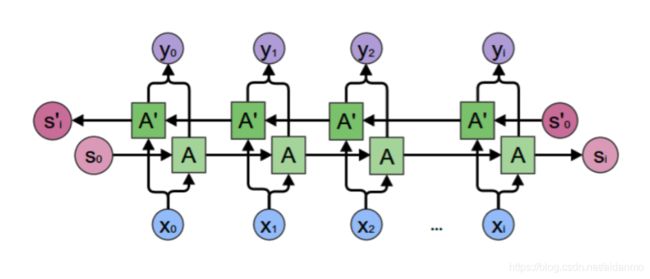
下图本别是RNN和LSTM的示意图:
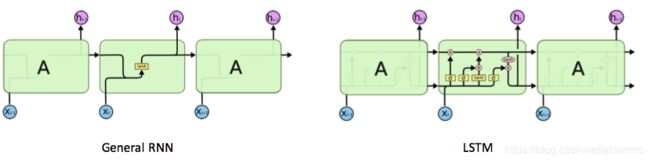
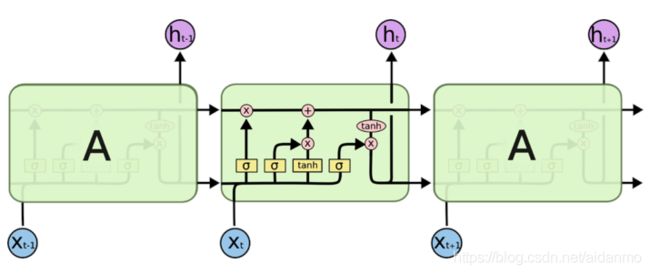
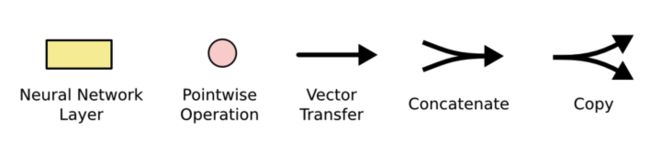
粉色的圈表示逐点(pointwise)操作,例如向量的和,黄色的矩阵表示学习到的神经网络层。
LSTM核心思想
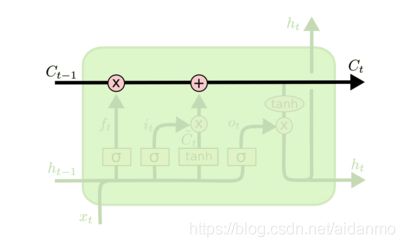
c t c_t ct表示细胞的在时刻t的状态,水平线则表示细胞的状态信息,它类似于一条传送带,直接在整个链上运行,只有一些少量的线性交互。信息在上面流转保持不变会很容易。
若只有上面的那条水平线是无法实现添加或者删除信息的。
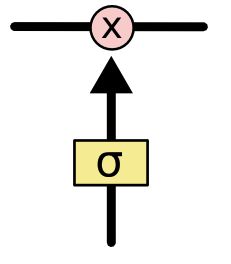
LSTM中的门可以选择性的控制信息的流动,通常由一个sigmoid神经网络层和一个point wise(或者叫element wise)的乘法操作组成。sigmoid层输出(一个向量)的每个元素都是一个0和1之间的实数,表示让对应信息通过的权重。
LSTM中主要包含三种门:遗忘门、输入门和输出门。
遗忘门
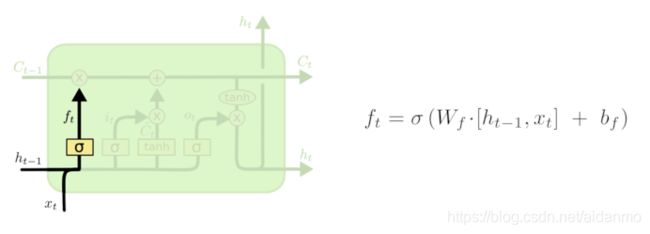
遗忘门的作用是让LSTM忘记之前没有用的信息。该结构会根据当前的输入 x t x_t xt、上一时刻的状态 c t − 1 c_{t-1} ct−1和上一时刻的输出 h t − 1 h_{t-1} ht−1共同决定哪一部分记忆需要被遗忘, σ \sigma σ表示sigmoid函数。
输入门
在LSTM忘记了部分之前的状态后,它还需要从当前的输入补充最新的记忆,这个过程就是输入门完成的。实现这个需要两个步骤:首先,一个叫做“input gate layer”的sigmoid层决定哪些信息需要更新;一个tanh层生成一个向量,也就是备选的用来更新的内容 C t ~ \widetilde{C_t} Ct 。
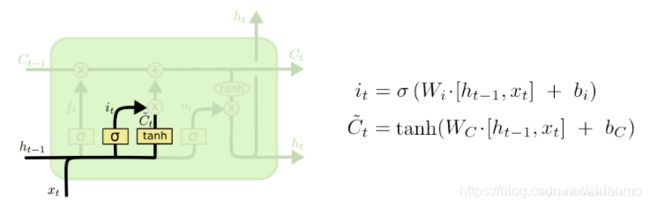
把遗忘门和输入门的结果进行整合,对cell的状态进行更新,可以得到当前时刻的状态 C t C_t Ct。
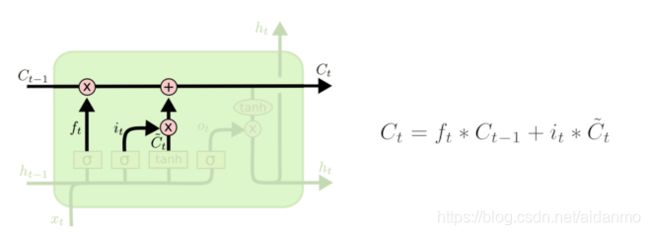
输出门
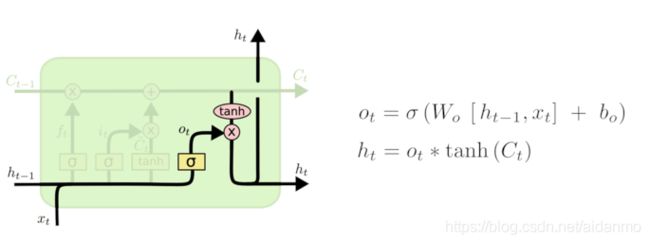
最终,我们需要确定输出什么值。首先,通过sigmoid层来确定细胞状态的哪个部分输出出去。接着,我们把cell状态通过tanh进行处理(得到一个-1到1之间的值)并将它和sigmoid门的输出相乘,输出结果。
LSTM的变种
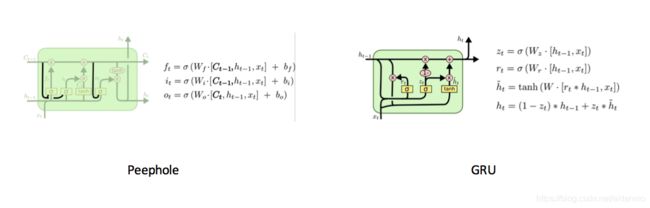
GRU(Gated Recurrent Unit)门限循环单元。是LSTM的简化版本,只有两个门:重置门和更新门。在这个结构中,把细胞状态(记忆单元 c t c_t ct)和隐藏状态(神经元活性 h t h_t ht)进行了合并。
更新门z:用来控制当前的状态需要遗忘多少信息和接受多少新信息。
重置门r:用来控制候选状态中有多少信息是从历史信息中得到的