Drailife

手动以及使用torch.nn实现前馈神经网络实验

其他文章

文章目录

一、任务1-手动实现前馈神经网络
- 1.1 任务内容
- 1.2 任务思路及代码
- - 1.2.0数据集定义
  - 1.2.1 手动实现前馈网络-回归任务
  - 1.2.2 手动前馈网络-二分类任务
  - 1.2.3 手动实现前馈神经网络-多分类
- 1.3 实验结果分析
二、任务2-利用torch.nn实现前馈神经网络
- 2.1 任务内容
- 2.2 任务思路及代码
- - 2.2.1 torch.nn实现前馈神经网络-回归任务
  - 2.2.2 torch.nn实现前馈神经网络-二分类
  - 2.2.3 torch.nn实现前馈神经网络-多分类任务
- 2.3 实验结果分析
三、任务3-在多分类任务中使用至少三种不同的激活函数
- 3.1 任务内容
- 3.2 任务思路及代码
- - 3.2.1画图函数
  - 3.2.1 使用Tanh激活函数
  - 3.2.2 使用Sigmoid激活函数
  - 3.2.3 使用ELU激活函数
- 3.3实验结果分析
三、任务4-对多分类任务中的模型评估隐藏层层数和隐藏单元个数对实验结果的影响
- 4.1 任务内容
- 4.2 任务思路及代码
- - 4.2.1一个隐藏层，神经元个数为[128]
  - 4.2.2 两个隐藏层，神经元个数分别为[512,256]
  - 4.2.3 四个隐藏层，神经元个数分别为[512,256,128,64]
- 4.3 实验结果分析
A1 实验心得

一、任务1-手动实现前馈神经网络

1.1 任务内容

任务具体要求
手动实现前馈神经网络解决上述回归、二分类、多分类任务
任务目的
学习前馈神经网络在回归、二分类和多分类任务上的应用
任务算法或原理介绍
前馈神经网络组成
任务所用数据集
回归任务数据集：
- 数据集的大小为10000且训练集大小为7000，测试集大小为3000，数据集的样本特征维度p为500，且服从如下的高维线性函数： $\sum_{i=1}^{p}0.0056x_i + \epsilon$
二分类数据集：
- 两个数据集的大小均为10000且训练集大小为7000，测试集大小为3000。
- 两个数据集的样本特征x的维度均为200，且分别服从均值互为相反数且方差相同的正态分布。
- 两个数据集的样本标签分别为0和1。
MNIST手写体数据集:
- 该数据集包含60,000个用于训练的图像样本和10,000个用于测试的图像样本。
- 图像是固定大小(28x28像素)，其值为0到1。为每个图像都被平展并转换为784

1.2 任务思路及代码

构建数据集
构建前馈神经网络，损失函数，优化函数
使用网络预测结果，得到损失值
进行反向传播，和梯度更新
对loss、acc等指标进行分析

1.2.0数据集定义

import time
import matplotlib.pyplot as plt
import numpy as np
import torch
import torch.nn as nn
import torchvision
from torch.nn.functional import cross_entropy, binary_cross_entropy
from torch.nn import CrossEntropyLoss
from torchvision import transforms
from sklearn import  metrics
device = torch.device("cuda" if torch.cuda.is_available() else "cpu") # 如果有gpu则在gpu上计算 加快计算速度
print(f'当前使用的device为{device}')
# 数据集定义
# 构建回归数据集合 - traindataloader1, testdataloader1
data_num, train_num, test_num = 10000, 7000, 3000 # 分别为样本总数量，训练集样本数量和测试集样本数量
true_w, true_b = 0.0056 * torch.ones(500,1), 0.028 
features = torch.randn(10000, 500)
labels = torch.matmul(features,true_w) + true_b # 按高斯分布
labels += torch.tensor(np.random.normal(0,0.01,size=labels.size()),dtype=torch.float32)
# 划分训练集和测试集
train_features, test_features = features[:train_num,:], features[train_num:,:]
train_labels, test_labels = labels[:train_num], labels[train_num:]
batch_size = 128
traindataset1 = torch.utils.data.TensorDataset(train_features,train_labels)
testdataset1 = torch.utils.data.TensorDataset(test_features, test_labels)
traindataloader1 = torch.utils.data.DataLoader(dataset=traindataset1,batch_size=batch_size,shuffle=True)
testdataloader1 = torch.utils.data.DataLoader(dataset=testdataset1,batch_size=batch_size,shuffle=True)

# 构二分类数据集合
data_num, train_num, test_num = 10000, 7000, 3000  # 分别为样本总数量，训练集样本数量和测试集样本数量
# 第一个数据集 符合均值为 0.5 标准差为1 得分布
features1 = torch.normal(mean=0.2, std=2, size=(data_num, 200), dtype=torch.float32)
labels1 = torch.ones(data_num)
# 第二个数据集 符合均值为 -0.5 标准差为1的分布
features2 = torch.normal(mean=-0.2, std=2, size=(data_num, 200), dtype=torch.float32)
labels2 = torch.zeros(data_num)

# 构建训练数据集
train_features2 = torch.cat((features1[:train_num], features2[:train_num]), dim=0)  # size torch.Size([14000, 200])
train_labels2 = torch.cat((labels1[:train_num], labels2[:train_num]), dim=-1)  # size  torch.Size([6000, 200])
# 构建测试数据集
test_features2 = torch.cat((features1[train_num:], features2[train_num:]), dim=0)  # torch.Size([14000])
test_labels2 = torch.cat((labels1[train_num:], labels2[train_num:]), dim=-1)  # torch.Size([6000])
batch_size = 128
# Build the training and testing dataset
traindataset2 = torch.utils.data.TensorDataset(train_features2, train_labels2)
testdataset2 = torch.utils.data.TensorDataset(test_features2, test_labels2)
traindataloader2 = torch.utils.data.DataLoader(dataset=traindataset2,batch_size=batch_size,shuffle=True)
testdataloader2 = torch.utils.data.DataLoader(dataset=testdataset2,batch_size=batch_size,shuffle=True)

# 定义多分类数据集 - train_dataloader - test_dataloader
batch_size = 128
# Build the training and testing dataset
traindataset3 = torchvision.datasets.FashionMNIST(root='E:\\DataSet\\FashionMNIST\\Train',
                                                  train=True,
                                                  download=True,
                                                  transform=transforms.ToTensor())
testdataset3 = torchvision.datasets.FashionMNIST(root='E:\\DataSet\\FashionMNIST\\Test',
                                                 train=False,
                                                 download=True,
                                                 transform=transforms.ToTensor())
traindataloader3 = torch.utils.data.DataLoader(traindataset3, batch_size=batch_size, shuffle=True)
testdataloader3 = torch.utils.data.DataLoader(testdataset3, batch_size=batch_size, shuffle=False)
# 绘制图像的代码
def picture(name, trainl, testl, type='Loss'):
    plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
    plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题
    plt.title(name) # 命名
    plt.plot(trainl, c='g', label='Train '+ type)
    plt.plot(testl, c='r', label='Test '+type)
    plt.xlabel('Epoch')
    plt.ylabel('Loss')
    plt.legend()
    plt.grid(True)
print(f'回归数据集   样本总数量{len(traindataset1) + len(testdataset1)},训练样本数量{len(traindataset1)},测试样本数量{len(testdataset1)}')
print(f'二分类数据集 样本总数量{len(traindataset2) + len(testdataset2)},训练样本数量{len(traindataset2)},测试样本数量{len(testdataset2)}')
print(f'多分类数据集 样本总数量{len(traindataset3) + len(testdataset3)},训练样本数量{len(traindataset3)},测试样本数量{len(testdataset3)}')

当前使用的device为cuda
回归数据集   样本总数量10000,训练样本数量7000,测试样本数量3000
二分类数据集 样本总数量20000,训练样本数量14000,测试样本数量6000
多分类数据集 样本总数量70000,训练样本数量60000,测试样本数量10000

1.2.1 手动实现前馈网络-回归任务

# 定义自己的前馈神经网络
class MyNet1():
    def __init__(self):
        # 设置隐藏层和输出层的节点数
        num_inputs, num_hiddens, num_outputs = 500, 256, 1
        w_1 = torch.tensor(np.random.normal(0,0.01,(num_hiddens,num_inputs)),dtype=torch.float32,requires_grad=True)
        b_1 = torch.zeros(num_hiddens, dtype=torch.float32,requires_grad=True)
        w_2 = torch.tensor(np.random.normal(0, 0.01,(num_outputs, num_hiddens)),dtype=torch.float32,requires_grad=True)
        b_2 = torch.zeros(num_outputs,dtype=torch.float32, requires_grad=True)
        self.params = [w_1, b_1, w_2, b_2]

        # 定义模型结构
        self.input_layer = lambda x: x.view(x.shape[0],-1)
        self.hidden_layer = lambda x: self.my_relu(torch.matmul(x,w_1.t())+b_1)
        self.output_layer = lambda x: torch.matmul(x,w_2.t()) + b_2

    def my_relu(self, x):
        return torch.max(input=x,other=torch.tensor(0.0))

    def forward(self,x):
        x = self.input_layer(x)
        x = self.my_relu(self.hidden_layer(x))
        x = self.output_layer(x)
        return x
def mySGD(params, lr, batchsize):
    for param in params:
        param.data -= lr*param.grad / batchsize

def mse(pred, true):
    ans = torch.sum((true-pred)**2) / len(pred)
    # print(ans)
    return ans

# 训练
model1 = MyNet1()  # logistics模型
criterion = CrossEntropyLoss()   # 损失函数
lr = 0.05   # 学习率
batchsize = 128 
epochs = 40 #训练轮数
train_all_loss1 = [] # 记录训练集上得loss变化
test_all_loss1 = [] #记录测试集上的loss变化
begintime1 = time.time()
for epoch in range(epochs):
    train_l = 0
    for data, labels in traindataloader1:
        pred = model1.forward(data)
        train_each_loss = mse(pred.view(-1,1), labels.view(-1,1)) #计算每次的损失值
        train_each_loss.backward() # 反向传播
        mySGD(model1.params, lr, batchsize) # 使用小批量随机梯度下降迭代模型参数
        # 梯度清零
        train_l += train_each_loss.item()
        for param in model1.params:
            param.grad.data.zero_()
        # print(train_each_loss)
    train_all_loss1.append(train_l) # 添加损失值到列表中
    with torch.no_grad():
        test_loss = 0
        for data, labels in traindataloader1:
            pred = model1.forward(data)
            test_each_loss = mse(pred, labels)
            test_loss += test_each_loss.item()
        test_all_loss1.append(test_loss)
    if epoch==0 or (epoch+1) % 4 == 0:
        print('epoch: %d | train loss:%.5f | test loss:%.5f'%(epoch+1,train_all_loss1[-1],test_all_loss1[-1]))
endtime1 = time.time()
print("手动实现前馈网络-回归实验 %d轮 总用时: %.3fs"%(epochs,endtime1-begintime1))

epoch: 1 | train loss:0.93475 | test loss:0.92674
epoch: 4 | train loss:0.90341 | test loss:0.89801
epoch: 8 | train loss:0.88224 | test loss:0.88125
epoch: 12 | train loss:0.87340 | test loss:0.87269
epoch: 16 | train loss:0.86727 | test loss:0.86776
epoch: 20 | train loss:0.86387 | test loss:0.86064
epoch: 24 | train loss:0.85918 | test loss:0.85865
epoch: 28 | train loss:0.85352 | test loss:0.85443
epoch: 32 | train loss:0.85082 | test loss:0.84960
epoch: 36 | train loss:0.84841 | test loss:0.84680
epoch: 40 | train loss:0.84312 | test loss:0.84205
手动实现前馈网络-回归实验 40轮 总用时: 9.466s

1.2.2 手动前馈网络-二分类任务

# 定义自己的前馈神经网络
class MyNet2():
    def __init__(self):
        # 设置隐藏层和输出层的节点数
        num_inputs, num_hiddens, num_outputs = 200, 256, 1
        w_1 = torch.tensor(np.random.normal(0, 0.01, (num_hiddens, num_inputs)), dtype=torch.float32,
                           requires_grad=True)
        b_1 = torch.zeros(num_hiddens, dtype=torch.float32, requires_grad=True)
        w_2 = torch.tensor(np.random.normal(0, 0.01, (num_outputs, num_hiddens)), dtype=torch.float32,
                           requires_grad=True)
        b_2 = torch.zeros(num_outputs, dtype=torch.float32, requires_grad=True)
        self.params = [w_1, b_1, w_2, b_2]

        # 定义模型结构
        self.input_layer = lambda x: x.view(x.shape[0], -1)
        self.hidden_layer = lambda x: self.my_relu(torch.matmul(x, w_1.t()) + b_1)
        self.output_layer = lambda x: torch.matmul(x, w_2.t()) + b_2
        self.fn_logistic = self.logistic

    def my_relu(self, x):
        return torch.max(input=x, other=torch.tensor(0.0))

    def logistic(self, x):  # 定义logistic函数
        x = 1.0 / (1.0 + torch.exp(-x))
        return x

    # 定义前向传播
    def forward(self, x):
        x = self.input_layer(x)
        x = self.my_relu(self.hidden_layer(x))
        x = self.fn_logistic(self.output_layer(x))
        return x


def mySGD(params, lr):
    for param in params:
        param.data -= lr * param.grad

# 训练
model2 = MyNet2()
lr = 0.01  # 学习率
epochs = 40  # 训练轮数
train_all_loss2 = []  # 记录训练集上得loss变化
test_all_loss2 = []  # 记录测试集上的loss变化
train_Acc12, test_Acc12 = [], []
begintime2 = time.time()
for epoch in range(epochs):
    train_l, train_epoch_count = 0, 0
    for data, labels in traindataloader2:
        pred = model2.forward(data)
        train_each_loss = binary_cross_entropy(pred.view(-1), labels.view(-1))  # 计算每次的损失值
        train_l += train_each_loss.item()
        train_each_loss.backward()  # 反向传播
        mySGD(model2.params, lr)  # 使用随机梯度下降迭代模型参数
        # 梯度清零
        for param in model2.params:
            param.grad.data.zero_()
        # print(train_each_loss)
        train_epoch_count += (torch.tensor(np.where(pred > 0.5, 1, 0)).view(-1) == labels).sum()
    train_Acc12.append((train_epoch_count/len(traindataset2)).item())
    train_all_loss2.append(train_l)  # 添加损失值到列表中
    with torch.no_grad():
        test_l, test_epoch_count = 0, 0
        for data, labels in testdataloader2:
            pred = model2.forward(data)
            test_each_loss = binary_cross_entropy(pred.view(-1), labels.view(-1))
            test_l += test_each_loss.item()
            test_epoch_count += (torch.tensor(np.where(pred > 0.5, 1, 0)).view(-1) == labels.view(-1)).sum()
        test_Acc12.append((test_epoch_count/len(testdataset2)).item())
        test_all_loss2.append(test_l)
    if epoch == 0 or (epoch + 1) % 4 == 0:
        print('epoch: %d | train loss:%.5f | test loss:%.5f | train acc:%.5f | test acc:%.5f'  % (epoch + 1, train_all_loss2[-1], test_all_loss2[-1], train_Acc12[-1], test_Acc12[-1]))
endtime2 = time.time()
print("手动实现前馈网络-二分类实验 %d轮 总用时: %.3f" % (epochs, endtime2 - begintime2))

epoch: 1 | train loss:74.73962 | test loss:30.99814 | train acc:0.73736 | test acc:0.87167
epoch: 4 | train loss:38.78090 | test loss:14.13814 | train acc:0.91657 | test acc:0.92167
epoch: 8 | train loss:22.69315 | test loss:9.54545 | train acc:0.92279 | test acc:0.92450
epoch: 12 | train loss:20.70577 | test loss:9.12440 | train acc:0.92700 | test acc:0.92333
epoch: 16 | train loss:19.60378 | test loss:9.08764 | train acc:0.92971 | test acc:0.92317
epoch: 20 | train loss:18.85067 | test loss:9.12393 | train acc:0.93321 | test acc:0.92167
epoch: 24 | train loss:18.14947 | test loss:9.16395 | train acc:0.93586 | test acc:0.92183
epoch: 28 | train loss:17.56800 | test loss:9.18966 | train acc:0.93864 | test acc:0.92183
epoch: 32 | train loss:16.92899 | test loss:9.21986 | train acc:0.94200 | test acc:0.92217
epoch: 36 | train loss:16.28683 | test loss:9.25284 | train acc:0.94493 | test acc:0.92267
epoch: 40 | train loss:15.61791 | test loss:9.29863 | train acc:0.94836 | test acc:0.92200
手动实现前馈网络-二分类实验 40轮 总用时: 12.668

1.2.3 手动实现前馈神经网络-多分类

# 定义自己的前馈神经网络
class MyNet3():
    def __init__(self):
        # 设置隐藏层和输出层的节点数
        num_inputs, num_hiddens, num_outputs = 28 * 28, 256, 10  # 十分类问题
        w_1 = torch.tensor(np.random.normal(0, 0.01, (num_hiddens, num_inputs)), dtype=torch.float32,
                           requires_grad=True)
        b_1 = torch.zeros(num_hiddens, dtype=torch.float32, requires_grad=True)
        w_2 = torch.tensor(np.random.normal(0, 0.01, (num_outputs, num_hiddens)), dtype=torch.float32,
                           requires_grad=True)
        b_2 = torch.zeros(num_outputs, dtype=torch.float32, requires_grad=True)
        self.params = [w_1, b_1, w_2, b_2]

        # 定义模型结构
        self.input_layer = lambda x: x.view(x.shape[0], -1)
        self.hidden_layer = lambda x: self.my_relu(torch.matmul(x, w_1.t()) + b_1)
        self.output_layer = lambda x: torch.matmul(x, w_2.t()) + b_2

    def my_relu(self, x):
        return torch.max(input=x, other=torch.tensor(0.0))

    # 定义前向传播
    def forward(self, x):
        x = self.input_layer(x)
        x = self.hidden_layer(x)
        x = self.output_layer(x)
        return x


def mySGD(params, lr, batchsize):
    for param in params:
        param.data -= lr * param.grad / batchsize

# 训练
model3 = MyNet3()  # logistics模型
criterion = cross_entropy  # 损失函数
lr = 0.15  # 学习率
epochs = 40  # 训练轮数
train_all_loss3 = []  # 记录训练集上得loss变化
test_all_loss3 = []  # 记录测试集上的loss变化
train_ACC13, test_ACC13 = [], [] # 记录正确的个数
begintime3 = time.time()
for epoch in range(epochs):
    train_l,train_acc_num = 0, 0
    for data, labels in traindataloader3:
        pred = model3.forward(data)
        train_each_loss = criterion(pred, labels)  # 计算每次的损失值
        train_l += train_each_loss.item()
        train_each_loss.backward()  # 反向传播
        mySGD(model3.params, lr, 128)  # 使用小批量随机梯度下降迭代模型参数
        # 梯度清零
        train_acc_num += (pred.argmax(dim=1)==labels).sum().item()
        for param in model3.params:
            param.grad.data.zero_()
        # print(train_each_loss)
    train_all_loss3.append(train_l)  # 添加损失值到列表中
    train_ACC13.append(train_acc_num / len(traindataset3)) # 添加准确率到列表中
    with torch.no_grad():
        test_l, test_acc_num = 0, 0
        for data, labels in testdataloader3:
            pred = model3.forward(data)
            test_each_loss = criterion(pred, labels)
            test_l += test_each_loss.item()
            test_acc_num += (pred.argmax(dim=1)==labels).sum().item()
        test_all_loss3.append(test_l)
        test_ACC13.append(test_acc_num / len(testdataset3))   # # 添加准确率到列表中
    if epoch == 0 or (epoch + 1) % 4 == 0:
        print('epoch: %d | train loss:%.5f | test loss:%.5f | train acc: %.2f | test acc: %.2f'
              % (epoch + 1, train_l, test_l, train_ACC13[-1],test_ACC13[-1]))
endtime3 = time.time()
print("手动实现前馈网络-多分类实验 %d轮 总用时: %.3f" % (epochs, endtime3 - begintime3))

epoch: 1 | train loss:1072.38118 | test loss:178.98460 | train acc: 0.16 | test acc: 0.23
epoch: 4 | train loss:937.98462 | test loss:151.17164 | train acc: 0.45 | test acc: 0.45
epoch: 8 | train loss:642.72610 | test loss:104.61924 | train acc: 0.61 | test acc: 0.61
epoch: 12 | train loss:500.75464 | test loss:83.06618 | train acc: 0.65 | test acc: 0.64
epoch: 16 | train loss:429.94874 | test loss:72.26618 | train acc: 0.67 | test acc: 0.67
epoch: 20 | train loss:390.61571 | test loss:66.21291 | train acc: 0.69 | test acc: 0.68
epoch: 24 | train loss:365.24224 | test loss:62.19734 | train acc: 0.71 | test acc: 0.70
epoch: 28 | train loss:346.34411 | test loss:59.15829 | train acc: 0.73 | test acc: 0.72
epoch: 32 | train loss:330.86975 | test loss:56.63529 | train acc: 0.75 | test acc: 0.74
epoch: 36 | train loss:317.64237 | test loss:54.49284 | train acc: 0.76 | test acc: 0.75
epoch: 40 | train loss:306.07250 | test loss:52.63789 | train acc: 0.77 | test acc: 0.77
手动实现前馈网络-多分类实验 40轮 总用时: 285.410

1.3 实验结果分析

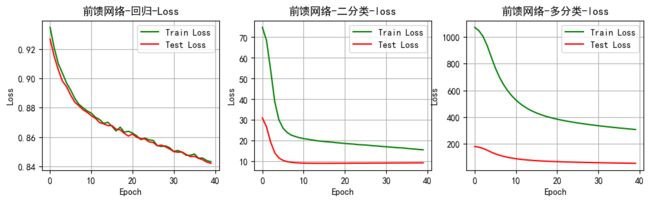
将上述前馈网络回归任务每一轮得训练和测试得损失值绘制成图表，如下图：

plt.figure(figsize=(12,3))
plt.title('Loss')
plt.subplot(131)
picture('前馈网络-回归-Loss',train_all_loss1,test_all_loss1)
plt.subplot(132)
picture('前馈网络-二分类-loss',train_all_loss2,test_all_loss2)
plt.subplot(133)
picture('前馈网络-多分类-loss',train_all_loss3,test_all_loss3)
plt.show()

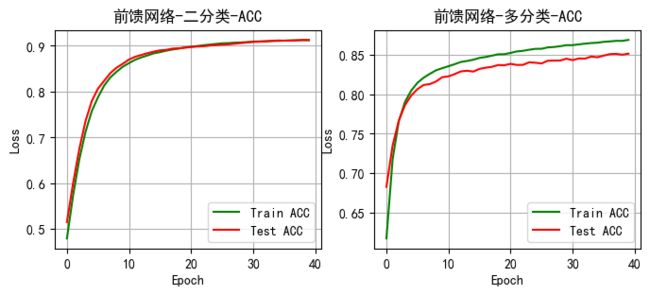
将上述的二分类和多分类的正确率绘制成表格

plt.figure(figsize=(8, 3))
plt.subplot(121)
picture('前馈网络-二分类-ACC',train_Acc12,test_Acc12,type='ACC')
plt.subplot(122)
picture('前馈网络-多分类—ACC', train_ACC13,test_ACC13, type='ACC')
plt.show()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-40l3VFzC-1668230795956)(file://D:\System_Default\桌面\前馈神经网络实验\output_14_0.png?msec=1668230466074)]

由上面的Loss曲线图和Acc曲线图可以看出手动构建的前馈神经网络在回归问题，二分类问题和多分类问题上具有很好的效果
Loss曲线呈不断下降的效果，其中在二分类上下降最快，在多分类上下降较缓。这和数据集的特性和数据量的大小有关系。
ACC曲线不断随着训练的次数增多不断增加，由于本次实验设置的训练轮数为40次，所以多分类的ACC较低，如继续增大训练轮数，准确率会继续增加

时间相关信息和准确率

Task	Epoch	Total Time	Max ACC
回归	40	9.466s	xxxxx
二分类	40	12.688s	0.92
多分类	40	285.410	0.77

可见模型不同的数据集上的训练时间不大相同，主要是由于数据集的大小不一样
在各种数据集上，loss总体呈现下降趋势，acc呈现上升趋势，由于局部最优点的存在，acc可能会出现一定的摆幅，但总体上增加

二、任务2-利用torch.nn实现前馈神经网络

2.1 任务内容

任务具体要求
利用torch.nn实现前馈神经网络解决上述回归、二分类、多分类任务
任务目的
利用torch.nn实现的前馈神经网络完成对应的回归、分类等任务
任务算法或原理介绍
见任务一
任务所用数据集（若此前已介绍过则可略）
见任务一

2.2 任务思路及代码

构建回归、二分类、多分类数据集
利用torch.nn构建前馈神经网络，损失函数，优化函数
使用网络预测结果，得到损失值
进行反向传播，和梯度更新
对loss、acc等指标进行分析

2.2.1 torch.nn实现前馈神经网络-回归任务

from torch.optim import SGD
from torch.nn import MSELoss
# 利用torch.nn实现前馈神经网络-回归任务 代码
# 定义自己的前馈神经网络
class MyNet21(nn.Module):
    def __init__(self):
        super(MyNet21, self).__init__()
        # 设置隐藏层和输出层的节点数
        num_inputs, num_hiddens, num_outputs = 500, 256, 1
        # 定义模型结构
        self.input_layer = nn.Flatten()
        self.hidden_layer = nn.Linear(num_inputs, num_hiddens)
        self.output_layer = nn.Linear(num_hiddens, num_outputs)
        self.relu = nn.ReLU()

    # 定义前向传播
    def forward(self, x):
        x = self.input_layer(x)
        x = self.relu(self.hidden_layer(x))
        x = self.output_layer(x)
        return x

# 训练
model21 = MyNet21()  # logistics模型
model21 = model21.to(device)
print(model21)
criterion = MSELoss()  # 损失函数
criterion = criterion.to(device)
optimizer = SGD(model21.parameters(), lr=0.1)  # 优化函数
epochs = 40  # 训练轮数
train_all_loss21 = []  # 记录训练集上得loss变化
test_all_loss21 = []  # 记录测试集上的loss变化
begintime21 = time.time()
for epoch in range(epochs):
    train_l = 0
    for data, labels in traindataloader1:
        data, labels = data.to(device=device), labels.to(device)
        pred = model21(data)
        train_each_loss = criterion(pred.view(-1, 1), labels.view(-1, 1))  # 计算每次的损失值
        optimizer.zero_grad()  # 梯度清零
        train_each_loss.backward()  # 反向传播
        optimizer.step()  # 梯度更新
        train_l += train_each_loss.item()
    train_all_loss21.append(train_l)  # 添加损失值到列表中
    with torch.no_grad():
        test_loss = 0
        for data, labels in testdataloader1:
            data, labels = data.to(device), labels.to(device)
            pred = model21(data)
            test_each_loss = criterion(pred,labels)
            test_loss += test_each_loss.item()
        test_all_loss21.append(test_loss)
    if epoch == 0 or (epoch + 1) % 10 == 0:
        print('epoch: %d | train loss:%.5f | test loss:%.5f' % (epoch + 1, train_all_loss21[-1], test_all_loss21[-1]))
endtime21 = time.time()
print("torch.nn实现前馈网络-回归实验 %d轮 总用时: %.3fs" % (epochs, endtime21 - begintime21))

MyNet21(
  (input_layer): Flatten(start_dim=1, end_dim=-1)
  (hidden_layer): Linear(in_features=500, out_features=256, bias=True)
  (output_layer): Linear(in_features=256, out_features=1, bias=True)
  (relu): ReLU()
)
epoch: 1 | train loss:179.20287 | test loss:0.46446
epoch: 10 | train loss:0.26332 | test loss:0.16052
epoch: 20 | train loss:0.16424 | test loss:0.14287
epoch: 30 | train loss:0.11388 | test loss:0.13307
epoch: 40 | train loss:0.08121 | test loss:0.13289
torch.nn实现前馈网络-回归实验 40轮 总用时: 6.538s

2.2.2 torch.nn实现前馈神经网络-二分类

# 利用torch.nn实现前馈神经网络-二分类任务
import time
from torch.optim import SGD
from torch.nn.functional import binary_cross_entropy
# 利用torch.nn实现前馈神经网络-回归任务 代码
# 定义自己的前馈神经网络
class MyNet22(nn.Module):
    def __init__(self):
        super(MyNet22, self).__init__()
        # 设置隐藏层和输出层的节点数
        num_inputs, num_hiddens, num_outputs = 200, 256, 1
        # 定义模型结构
        self.input_layer = nn.Flatten()
        self.hidden_layer = nn.Linear(num_inputs, num_hiddens)
        self.output_layer = nn.Linear(num_hiddens, num_outputs)
        self.relu = nn.ReLU()

    def logistic(self, x):  # 定义logistic函数
        x = 1.0 / (1.0 + torch.exp(-x))
        return x
    # 定义前向传播
    def forward(self, x):
        x = self.input_layer(x)
        x = self.relu(self.hidden_layer(x))
        x = self.logistic(self.output_layer(x))
        return x

# 训练
model22 = MyNet22()  # logistics模型
model22 = model22.to(device)
print(model22)
optimizer = SGD(model22.parameters(), lr=0.001)  # 优化函数
epochs = 40  # 训练轮数
train_all_loss22 = []  # 记录训练集上得loss变化
test_all_loss22 = []  # 记录测试集上的loss变化
train_ACC22, test_ACC22 = [], []
begintime22 = time.time()
for epoch in range(epochs):
    train_l, train_epoch_count, test_epoch_count = 0, 0, 0 # 每一轮的训练损失值 训练集正确个数 测试集正确个数
    for data, labels in traindataloader2:
        data, labels = data.to(device), labels.to(device)
        pred = model22(data)
        train_each_loss = binary_cross_entropy(pred.view(-1), labels.view(-1))  # 计算每次的损失值
        optimizer.zero_grad()  # 梯度清零
        train_each_loss.backward()  # 反向传播
        optimizer.step()  # 梯度更新
        train_l += train_each_loss.item()
        pred = torch.tensor(np.where(pred.cpu()>0.5, 1, 0))  # 大于 0.5时候，预测标签为 1 否则为0
        each_count = (pred.view(-1) == labels.cpu()).sum() # 每一个batchsize的正确个数
        train_epoch_count += each_count # 计算每个epoch上的正确个数
    train_ACC22.append(train_epoch_count / len(traindataset2))
    train_all_loss22.append(train_l)  # 添加损失值到列表中
    with torch.no_grad():
        test_loss, each_count = 0, 0
        for data, labels in testdataloader2:
            data, labels = data.to(device), labels.to(device)
            pred = model22(data)
            test_each_loss = binary_cross_entropy(pred.view(-1),labels)
            test_loss += test_each_loss.item()
            # .cpu 为转换到cpu上计算
            pred = torch.tensor(np.where(pred.cpu() > 0.5, 1, 0))
            each_count = (pred.view(-1)==labels.cpu().view(-1)).sum()
            test_epoch_count += each_count
        test_all_loss22.append(test_loss)
        test_ACC22.append(test_epoch_count / len(testdataset2))
    if epoch == 0 or (epoch + 1) % 4 == 0:
        print('epoch: %d | train loss:%.5f test loss:%.5f | train acc:%.5f | test acc:%.5f' % (epoch + 1, train_all_loss22[-1], 
                                                                                               test_all_loss22[-1], train_ACC22[-1], test_ACC22[-1]))

endtime22 = time.time()
print("torch.nn实现前馈网络-二分类实验 %d轮 总用时: %.3fs" % (epochs, endtime22 - begintime22))

MyNet22(
  (input_layer): Flatten(start_dim=1, end_dim=-1)
  (hidden_layer): Linear(in_features=200, out_features=256, bias=True)
  (output_layer): Linear(in_features=256, out_features=1, bias=True)
  (relu): ReLU()
)
epoch: 1 | train loss:79.07320 test loss:32.92679 | train acc:0.47936 | test acc:0.51533
epoch: 4 | train loss:67.24074 test loss:28.13028 | train acc:0.71221 | test acc:0.73583
epoch: 8 | train loss:56.03760 test loss:23.48878 | train acc:0.83114 | test acc:0.84050
epoch: 12 | train loss:47.73045 test loss:20.03178 | train acc:0.86971 | test acc:0.87617
epoch: 16 | train loss:41.48397 test loss:17.45700 | train acc:0.88629 | test acc:0.89017
epoch: 20 | train loss:36.86592 test loss:15.55864 | train acc:0.89643 | test acc:0.89600
epoch: 24 | train loss:33.54197 test loss:14.16518 | train acc:0.90271 | test acc:0.90067
epoch: 28 | train loss:31.02676 test loss:13.14387 | train acc:0.90700 | test acc:0.90467
epoch: 32 | train loss:29.09306 test loss:12.38178 | train acc:0.90971 | test acc:0.90917
epoch: 36 | train loss:27.60086 test loss:11.78166 | train acc:0.91136 | test acc:0.91133
epoch: 40 | train loss:26.49638 test loss:11.34545 | train acc:0.91279 | test acc:0.91233
torch.nn实现前馈网络-二分类实验 40轮 总用时: 15.395s

2.2.3 torch.nn实现前馈神经网络-多分类任务

# 利用torch.nn实现前馈神经网络-多分类任务
from collections import OrderedDict
from torch.nn import CrossEntropyLoss
from torch.optim import SGD
# 定义自己的前馈神经网络
class MyNet23(nn.Module):
    """
    参数：  num_input：输入每层神经元个数，为一个列表数据
            num_hiddens：隐藏层神经元个数
            num_outs： 输出层神经元个数
            num_hiddenlayer : 隐藏层的个数
    """
    def __init__(self,num_hiddenlayer=1, num_inputs=28*28,num_hiddens=[256],num_outs=10,act='relu'):
        super(MyNet23, self).__init__()
        # 设置隐藏层和输出层的节点数
        self.num_inputs, self.num_hiddens, self.num_outputs = num_inputs,num_hiddens,num_outs # 十分类问题

        # 定义模型结构
        self.input_layer = nn.Flatten()
        # 若只有一层隐藏层
        if num_hiddenlayer ==1:
            self.hidden_layers = nn.Linear(self.num_inputs,self.num_hiddens[-1])
        else: # 若有多个隐藏层
            self.hidden_layers = nn.Sequential()
            self.hidden_layers.add_module("hidden_layer1", nn.Linear(self.num_inputs,self.num_hiddens[0]))
            for i in range(0,num_hiddenlayer-1):
                name = str('hidden_layer'+str(i+2))
                self.hidden_layers.add_module(name, nn.Linear(self.num_hiddens[i],self.num_hiddens[i+1]))
        self.output_layer = nn.Linear(self.num_hiddens[-1], self.num_outputs)
        # 指代需要使用什么样子的激活函数
        if act == 'relu':
            self.act = nn.ReLU()
        elif act == 'sigmoid':
            self.act = nn.Sigmoid()
        elif act == 'tanh':
            self.act = nn.Tanh()
        elif act == 'elu':
            self.act = nn.ELU()
        print(f'你本次使用的激活函数为 {act}')

    def logistic(self, x):  # 定义logistic函数
        x = 1.0 / (1.0 + torch.exp(-x))
        return x
    # 定义前向传播
    def forward(self, x):
        x = self.input_layer(x)
        x = self.act(self.hidden_layers(x))
        x = self.output_layer(x)
        return x

# 训练
# 使用默认的参数即： num_inputs=28*28,num_hiddens=256,num_outs=10,act='relu'
model23 = MyNet23()  
model23 = model23.to(device)

# 将训练过程定义为一个函数，方便实验三和实验四调用
def train_and_test(model=model23):
    MyModel = model
    print(MyModel)
    optimizer = SGD(MyModel.parameters(), lr=0.01)  # 优化函数
    epochs = 40  # 训练轮数
    criterion = CrossEntropyLoss() # 损失函数
    train_all_loss23 = []  # 记录训练集上得loss变化
    test_all_loss23 = []  # 记录测试集上的loss变化
    train_ACC23, test_ACC23 = [], []
    begintime23 = time.time()
    for epoch in range(epochs):
        train_l, train_epoch_count, test_epoch_count = 0, 0, 0
        for data, labels in traindataloader3:
            data, labels = data.to(device), labels.to(device)
            pred = MyModel(data)
            train_each_loss = criterion(pred, labels.view(-1))  # 计算每次的损失值
            optimizer.zero_grad()  # 梯度清零
            train_each_loss.backward()  # 反向传播
            optimizer.step()  # 梯度更新
            train_l += train_each_loss.item()
            train_epoch_count += (pred.argmax(dim=1)==labels).sum()
        train_ACC23.append(train_epoch_count.cpu()/len(traindataset3))
        train_all_loss23.append(train_l)  # 添加损失值到列表中
        with torch.no_grad():
            test_loss, test_epoch_count= 0, 0
            for data, labels in testdataloader3:
                data, labels = data.to(device), labels.to(device)
                pred = MyModel(data)
                test_each_loss = criterion(pred,labels)
                test_loss += test_each_loss.item()
                test_epoch_count += (pred.argmax(dim=1)==labels).sum()
            test_all_loss23.append(test_loss)
            test_ACC23.append(test_epoch_count.cpu()/len(testdataset3))
        if epoch == 0 or (epoch + 1) % 4 == 0:
            print('epoch: %d | train loss:%.5f | test loss:%.5f | train acc:%5f test acc:%.5f:' % (epoch + 1, train_all_loss23[-1], test_all_loss23[-1],
                                                                                                                     train_ACC23[-1],test_ACC23[-1]))
    endtime23 = time.time()
    print("torch.nn实现前馈网络-多分类任务 %d轮 总用时: %.3fs" % (epochs, endtime23 - begintime23))
    # 返回训练集和测试集上的 损失值 与 准确率
    return train_all_loss23,test_all_loss23,train_ACC23,test_ACC23
train_all_loss23,test_all_loss23,train_ACC23,test_ACC23 = train_and_test(model=model23)

你本次使用的激活函数为 relu
MyNet23(
  (input_layer): Flatten(start_dim=1, end_dim=-1)
  (hidden_layers): Linear(in_features=784, out_features=256, bias=True)
  (output_layer): Linear(in_features=256, out_features=10, bias=True)
  (act): ReLU()
)
epoch: 1 | train loss:657.80222 | test loss:74.67226 | train acc:0.617033 test acc:0.68250:
epoch: 4 | train loss:294.04037 | test loss:49.02613 | train acc:0.790417 test acc:0.78640:
epoch: 8 | train loss:240.90404 | test loss:42.03059 | train acc:0.825967 test acc:0.81290:
epoch: 12 | train loss:220.93427 | test loss:38.98449 | train acc:0.838167 test acc:0.82560:
epoch: 16 | train loss:209.56696 | test loss:37.69722 | train acc:0.846100 test acc:0.83220:
epoch: 20 | train loss:201.51846 | test loss:36.26622 | train acc:0.850833 test acc:0.83680:
epoch: 24 | train loss:195.08846 | test loss:35.30845 | train acc:0.856483 test acc:0.84050:
epoch: 28 | train loss:189.75432 | test loss:34.98433 | train acc:0.859967 test acc:0.84270:
epoch: 32 | train loss:185.09050 | test loss:34.47698 | train acc:0.863317 test acc:0.84540:
epoch: 36 | train loss:181.01641 | test loss:33.44194 | train acc:0.866517 test acc:0.84900:
epoch: 40 | train loss:177.54666 | test loss:33.11320 | train acc:0.868933 test acc:0.85150:
torch.nn实现前馈网络-多分类任务 40轮 总用时: 282.329s

2.3 实验结果分析

将上述前馈网络回归任务每一轮得训练和测试得损失值绘制成图表，如下图：

plt.figure(figsize=(12,3))
plt.subplot(131)
picture('前馈网络-回归-loss',train_all_loss21,test_all_loss21)
plt.subplot(132)
picture('前馈网络-二分类-loss',train_all_loss22,test_all_loss22)
plt.subplot(133)
picture('前馈网络-多分类-loss',train_all_loss23,test_all_loss23)
plt.show()

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8Snas3rX-1668230795957)(file://D:\System_Default\桌面\前馈神经网络实验\output_25_0.png?msec=1668230466074)]

将上述前馈网络回归任务每一轮得训练和测试得准确率值绘制成图表，如下图：

plt.figure(figsize=(8,3))
plt.subplot(121)
picture('前馈网络-二分类-ACC',train_ACC22,test_ACC22,type='ACC')
plt.subplot(122)
picture('前馈网络-多分类-ACC',train_ACC23,test_ACC23,type='ACC')
plt.show()

torch.nn实现的前馈网络在不同的数据集上表现出不同的效果，在回归问题中，损失函数下降速度极快，在前几轮就充分训练模型，并取得较好的效果。
在二分类中，loss值稳步下降，准确率逐步提升。
在多分类中，数据的规模较大，loss值在前6轮中下降较快，准确率提升较大，在后续的训练中，loss值相比前几轮下降较慢，准确率提升速度也不及前几轮。同时由于训练轮数的不足，模型并未没被完全训练好，可以通过增大epochs和lr来解决这个问题。

三、任务3-在多分类任务中使用至少三种不同的激活函数

3.1 任务内容

任务具体要求
在上述实现的多分类任务中使用至少三种不同的激活函数，本次实验使用分别使用四个激活函数：Relu、Tanh、Sigmoid、ELU
任务目的
学习不同激活函数的作用
任务算法或原理介绍
同任务二中多分类
任务所用数据集（若此前已介绍过则可略）
同见任务二中多分类数据集

3.2 任务思路及代码

构建回归、二分类、多分类数据集
利用torch.nn构建前馈神经网络，损失函数，优化函数
构建不同的激活函数
使用网络预测结果，得到损失值
进行反向传播，和梯度更新
对loss、acc等指标进行分析

默认的网络为一个隐藏层，神经元个数为[256],激活函数为relu函数

3.2.1画图函数

def ComPlot(datalist,title='1',ylabel='Loss',flag='act'):
    plt.rcParams["font.sans-serif"]=["SimHei"] #设置字体
    plt.rcParams["axes.unicode_minus"]=False #该语句解决图像中的“-”负号的乱码问题
    plt.title(title)
    plt.xlabel('Epoch')
    plt.ylabel(ylabel)
    plt.plot(datalist[0],label='Tanh' if flag=='act' else '[128]')
    plt.plot(datalist[1],label='Sigmoid' if flag=='act' else '[512 256]')
    plt.plot(datalist[2],label='ELu' if flag=='act' else '[512 256 128 64]')
    plt.plot(datalist[3],label='Relu' if flag=='act' else '[256]')
    plt.legend()
    plt.grid(True)

3.2.1 使用Tanh激活函数

# 使用实验二中多分类的模型定义其激活函数为 Tanh
model31 = MyNet23(1,28*28,[256],10,act='tanh') 
model31 = model31.to(device) # 若有gpu则放在gpu上训练
# 调用实验二中定义的训练函数，避免重复编写代码
train_all_loss31,test_all_loss31,train_ACC31,test_ACC31 = train_and_test(model=model31)

你本次使用的激活函数为 tanh
MyNet23(
  (input_layer): Flatten(start_dim=1, end_dim=-1)
  (hidden_layers): Linear(in_features=784, out_features=256, bias=True)
  (output_layer): Linear(in_features=256, out_features=10, bias=True)
  (act): Tanh()
)
epoch: 1 | train loss:614.44055 | test loss:72.26356 | train acc:0.635750 test acc:0.69720:
epoch: 4 | train loss:288.82626 | test loss:48.12523 | train acc:0.795517 test acc:0.79060:
epoch: 8 | train loss:238.00103 | test loss:41.35938 | train acc:0.826917 test acc:0.81620:
epoch: 12 | train loss:218.78028 | test loss:38.68566 | train acc:0.838517 test acc:0.82570:
epoch: 16 | train loss:207.86982 | test loss:37.10549 | train acc:0.845550 test acc:0.83370:
epoch: 20 | train loss:200.26399 | test loss:36.04159 | train acc:0.850883 test acc:0.83600:
epoch: 24 | train loss:194.53169 | test loss:35.21199 | train acc:0.854200 test acc:0.84010:
epoch: 28 | train loss:189.79102 | test loss:34.56415 | train acc:0.857767 test acc:0.84210:
epoch: 32 | train loss:185.85091 | test loss:33.98912 | train acc:0.860000 test acc:0.84430:
epoch: 36 | train loss:182.23084 | test loss:33.53722 | train acc:0.862267 test acc:0.84570:
epoch: 40 | train loss:179.19994 | test loss:33.02570 | train acc:0.864867 test acc:0.84950:
torch.nn实现前馈网络-多分类任务 40轮 总用时: 276.785s

3.2.2 使用Sigmoid激活函数

# 使用实验二中多分类的模型定义其激活函数为 Sigmoid
model32 = MyNet23(1,28*28,[256],10,act='sigmoid') 
model32 = model32.to(device) # 若有gpu则放在gpu上训练
# 调用实验二中定义的训练函数，避免重复编写代码
train_all_loss32,test_all_loss32,train_ACC32,test_ACC32 = train_and_test(model=model32)

你本次使用的激活函数为 sigmoid
MyNet23(
  (input_layer): Flatten(start_dim=1, end_dim=-1)
  (hidden_layers): Linear(in_features=784, out_features=256, bias=True)
  (output_layer): Linear(in_features=256, out_features=10, bias=True)
  (act): Sigmoid()
)
epoch: 1 | train loss:995.80085 | test loss:150.25593 | train acc:0.435450 test acc:0.59430:
epoch: 4 | train loss:522.85408 | test loss:82.88827 | train acc:0.695683 test acc:0.69070:
epoch: 8 | train loss:370.86663 | test loss:61.70778 | train acc:0.738917 test acc:0.73290:
epoch: 12 | train loss:321.10749 | test loss:54.31158 | train acc:0.758450 test acc:0.75520:
epoch: 16 | train loss:294.92375 | test loss:50.29494 | train acc:0.775283 test acc:0.76910:
epoch: 20 | train loss:276.84129 | test loss:47.50861 | train acc:0.790217 test acc:0.78500:
epoch: 24 | train loss:263.20515 | test loss:45.42484 | train acc:0.800983 test acc:0.79580:
epoch: 28 | train loss:252.69126 | test loss:43.83572 | train acc:0.810400 test acc:0.80020:
epoch: 32 | train loss:244.45354 | test loss:42.66255 | train acc:0.817433 test acc:0.80570:
epoch: 36 | train loss:237.77932 | test loss:41.69042 | train acc:0.822250 test acc:0.80920:
epoch: 40 | train loss:232.28827 | test loss:40.81849 | train acc:0.826767 test acc:0.81430:
torch.nn实现前馈网络-多分类任务 40轮 总用时: 275.495s

3.2.3 使用ELU激活函数

# 使用实验二中多分类的模型定义其激活函数为 ELU
model33 = MyNet23(1,28*28,[256],10,act='elu') 
model33 = model33.to(device) # 若有gpu则放在gpu上训练
# 调用实验二中定义的训练函数，避免重复编写代码m
train_all_loss33,test_all_loss33,train_ACC33,test_ACC33 = train_and_test(model=model33)

你本次使用的激活函数为 elu
MyNet23(
  (input_layer): Flatten(start_dim=1, end_dim=-1)
  (hidden_layers): Linear(in_features=784, out_features=256, bias=True)
  (output_layer): Linear(in_features=256, out_features=10, bias=True)
  (act): ELU(alpha=1.0)
)
epoch: 1 | train loss:614.85905 | test loss:71.33988 | train acc:0.622367 test acc:0.68490:
epoch: 4 | train loss:287.24690 | test loss:48.03733 | train acc:0.796583 test acc:0.79180:
epoch: 8 | train loss:239.79761 | test loss:41.75318 | train acc:0.826650 test acc:0.81640:
epoch: 12 | train loss:221.79838 | test loss:39.30922 | train acc:0.837183 test acc:0.82830:
epoch: 16 | train loss:211.67667 | test loss:37.82760 | train acc:0.843600 test acc:0.83100:
epoch: 20 | train loss:205.04718 | test loss:36.92112 | train acc:0.849783 test acc:0.83580:
epoch: 24 | train loss:199.93171 | test loss:36.18179 | train acc:0.852900 test acc:0.83730:
epoch: 28 | train loss:195.87270 | test loss:35.63731 | train acc:0.855517 test acc:0.83860:
epoch: 32 | train loss:192.41613 | test loss:35.19403 | train acc:0.858200 test acc:0.84070:
epoch: 36 | train loss:189.43485 | test loss:34.66838 | train acc:0.859967 test acc:0.84310:
epoch: 40 | train loss:186.66312 | test loss:34.41900 | train acc:0.862283 test acc:0.84550:
torch.nn实现前馈网络-多分类任务 40轮 总用时: 275.706s

3.3实验结果分析

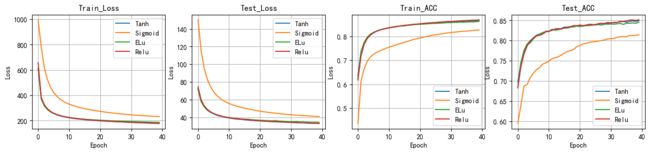
对比使用不同的激活函数得到的loss曲线值和正确率

plt.figure(figsize=(16,3))
plt.subplot(141)
ComPlot([train_all_loss31,train_all_loss32,train_all_loss33,train_all_loss23],title='Train_Loss')
plt.subplot(142)
ComPlot([test_all_loss31,test_all_loss32,test_all_loss33,test_all_loss23],title='Test_Loss')
plt.subplot(143)
ComPlot([train_ACC31,train_ACC32,train_ACC33,train_ACC23],title='Train_ACC')
plt.subplot(144)
ComPlot([test_ACC31,test_ACC32,test_ACC33,test_ACC23],title='Test_ACC')
plt.show()

由上图loss值得变化和acc的变化，我们可以看出使用不同的激活函数构建的模型具有不同的效果
在本次实验中，四种损失函数的loss结果不断下降，acc值总体上随epoch呈上升趋势，但是两者的变化的速度随着epoch有着不同的表现。
由上图可清晰看出激活函数’Relu’,'Tanh’和’ELU’三者的曲线接近，在最后几轮epoch上的表现略有不同。在loss值和acc方面，但Sigmoid激活函数在minist数据集上的表现不如前三者。故对于该多分类数据集推荐使用前三者激活函数，效果会更好。
应用不同激活函数的模型的训练时间

Act	Time	Acc	Rank
Relu	282.329s	0.851	1
Tanh	276.785s	0.849	2
Sigmoid	275.495s	0.814	4
ELU	275.706s	.8455	3

可以看出不同的激活函数，模型的训练时间会有较小的差异，ACC也有差异，其中表现最好的为Relu函数，表现最差的是Sigmoid激活函数

三、任务4-对多分类任务中的模型评估隐藏层层数和隐藏单元个数对实验结果的影响

4.1 任务内容

任务具体要求
使用不同的隐藏层层数和隐藏单元个数，进行对比实验并分析实验结果，为了体现控制变量原则，统一使用RELU为激活函数
任务目的
学习不同激活函数的作用
任务算法或原理介绍
同任务二中多分类
任务所用数据集（若此前已介绍过则可略）
同见任务二中多分类数据集

4.2 任务思路及代码

构建多分类数据集
利用torch.nn构建前馈神经网络，损失函数，优化函数
构建不同的隐藏层和隐藏神经元个数
使用网络预测结果，得到损失值
进行反向传播，和梯度更新
对loss、acc等指标进行分析

默认的网络为一个隐藏层，神经元个数为[256],激活函数为relu函数

4.2.1一个隐藏层，神经元个数为[128]

# 使用实验二中多分类的模型  一个隐藏层，神经元个数为[128]
model41 = MyNet23(1,28*28,[128],10,act='relu') 
model41 = model41.to(device) # 若有gpu则放在gpu上训练
# 调用实验二中定义的训练函数，避免重复编写代码
train_all_loss41,test_all_loss41,train_ACC41,test_ACC41 = train_and_test(model=model41)

你本次使用的激活函数为 relu
MyNet23(
  (input_layer): Flatten(start_dim=1, end_dim=-1)
  (hidden_layers): Linear(in_features=784, out_features=128, bias=True)
  (output_layer): Linear(in_features=128, out_features=10, bias=True)
  (act): ReLU()
)
epoch: 1 | train loss:679.69445 | test loss:75.43487 | train acc:0.593267 test acc:0.67750:
epoch: 4 | train loss:296.15307 | test loss:49.17869 | train acc:0.788883 test acc:0.78460:
epoch: 8 | train loss:242.33678 | test loss:42.06035 | train acc:0.825617 test acc:0.81300:
epoch: 12 | train loss:221.84079 | test loss:39.23156 | train acc:0.837867 test acc:0.82340:
epoch: 16 | train loss:210.24818 | test loss:37.37779 | train acc:0.845400 test acc:0.83350:
epoch: 20 | train loss:201.90868 | test loss:36.61562 | train acc:0.850933 test acc:0.83330:
epoch: 24 | train loss:195.41365 | test loss:35.32518 | train acc:0.856033 test acc:0.84170:
epoch: 28 | train loss:190.04806 | test loss:34.82272 | train acc:0.859617 test acc:0.84480:
epoch: 32 | train loss:185.48290 | test loss:34.17104 | train acc:0.863700 test acc:0.84790:
epoch: 36 | train loss:181.42996 | test loss:33.58404 | train acc:0.866400 test acc:0.85040:
epoch: 40 | train loss:177.64588 | test loss:32.95457 | train acc:0.868917 test acc:0.85340:
torch.nn实现前馈网络-多分类任务 40轮 总用时: 256.331s

4.2.2 两个隐藏层，神经元个数分别为[512,256]

# 使用实验二中多分类的模型 两个隐藏层，神经元个数为[512，256]
model42 = MyNet23(2,28*28,[512,256],10,act='relu') 
model42 = model42.to(device) # 若有gpu则放在gpu上训练
# 调用实验二中定义的训练函数，避免重复编写代码
train_all_loss42,test_all_loss42,train_ACC42,test_ACC42 = train_and_test(model=model42)

你本次使用的激活函数为 relu
MyNet23(
  (input_layer): Flatten(start_dim=1, end_dim=-1)
  (hidden_layers): Sequential(
    (hidden_layer1): Linear(in_features=784, out_features=512, bias=True)
    (hidden_layer2): Linear(in_features=512, out_features=256, bias=True)
  )
  (output_layer): Linear(in_features=256, out_features=10, bias=True)
  (act): ReLU()
)
epoch: 1 | train loss:721.23681 | test loss:77.65762 | train acc:0.597033 test acc:0.66200:
epoch: 4 | train loss:290.02748 | test loss:48.21799 | train acc:0.785700 test acc:0.78350:
epoch: 8 | train loss:233.58869 | test loss:40.98045 | train acc:0.827000 test acc:0.81450:
epoch: 12 | train loss:214.90069 | test loss:38.51032 | train acc:0.840033 test acc:0.82750:
epoch: 16 | train loss:204.69288 | test loss:37.38850 | train acc:0.847967 test acc:0.83400:
epoch: 20 | train loss:197.78729 | test loss:35.71079 | train acc:0.853783 test acc:0.84090:
epoch: 24 | train loss:191.70526 | test loss:35.84411 | train acc:0.857483 test acc:0.83980:
epoch: 28 | train loss:187.40948 | test loss:34.54823 | train acc:0.861317 test acc:0.84490:
epoch: 32 | train loss:182.39799 | test loss:33.89679 | train acc:0.864967 test acc:0.84980:
epoch: 36 | train loss:179.16446 | test loss:33.09553 | train acc:0.867117 test acc:0.85320:
epoch: 40 | train loss:175.48380 | test loss:32.61282 | train acc:0.869417 test acc:0.85420:
torch.nn实现前馈网络-多分类任务 40轮 总用时: 278.211s

4.2.3 四个隐藏层，神经元个数分别为[512,256,128,64]

# 使用实验二中多分类的模型  四个隐藏层，神经元个数为[512，256，128，64]
model43 = MyNet23(3,28*28,[512,256,128],10,act='relu') 
model43 = model43.to(device) # 若有gpu则放在gpu上训练
# 调用实验二中定义的训练函数，避免重复编写代码
train_all_loss43,test_all_loss43,train_ACC43,test_ACC43 = train_and_test(model=model43)

你本次使用的激活函数为 relu
MyNet23(
  (input_layer): Flatten(start_dim=1, end_dim=-1)
  (hidden_layers): Sequential(
    (hidden_layer1): Linear(in_features=784, out_features=512, bias=True)
    (hidden_layer2): Linear(in_features=512, out_features=256, bias=True)
    (hidden_layer3): Linear(in_features=256, out_features=128, bias=True)
  )
  (output_layer): Linear(in_features=128, out_features=10, bias=True)
  (act): ReLU()
)
epoch: 1 | train loss:826.53139 | test loss:91.98144 | train acc:0.439383 test acc:0.59060:
epoch: 4 | train loss:308.51752 | test loss:50.76393 | train acc:0.762300 test acc:0.76810:
epoch: 8 | train loss:240.67431 | test loss:41.38339 | train acc:0.819217 test acc:0.81350:
epoch: 12 | train loss:218.27895 | test loss:39.66492 | train acc:0.835900 test acc:0.82200:
epoch: 16 | train loss:205.91386 | test loss:36.80909 | train acc:0.845617 test acc:0.83080:
epoch: 20 | train loss:197.43931 | test loss:35.69519 | train acc:0.852383 test acc:0.83730:
epoch: 24 | train loss:191.46616 | test loss:37.09589 | train acc:0.857333 test acc:0.83610:
epoch: 28 | train loss:186.57159 | test loss:34.91067 | train acc:0.860400 test acc:0.84470:
epoch: 32 | train loss:181.72905 | test loss:33.75175 | train acc:0.863333 test acc:0.85110:
epoch: 36 | train loss:177.50958 | test loss:33.11897 | train acc:0.866917 test acc:0.84950:
epoch: 40 | train loss:174.15993 | test loss:32.97797 | train acc:0.868233 test acc:0.85210:
torch.nn实现前馈网络-多分类任务 40轮 总用时: 269.510s

4.3 实验结果分析

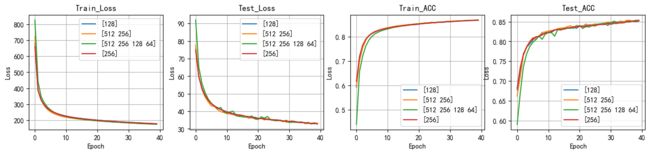
对比使用不同的隐藏层和隐藏神经元个数得到的loss曲线值和正确率

plt.figure(figsize=(16,3))
plt.subplot(141)
ComPlot([train_all_loss41,train_all_loss42,train_all_loss43,train_all_loss23],title='Train_Loss',flag='hidden')
plt.subplot(142)
ComPlot([test_all_loss41,test_all_loss42,test_all_loss43,test_all_loss23],title='Test_Loss',flag='hidden')
plt.subplot(143)
ComPlot([train_ACC41,train_ACC42,train_ACC43,train_ACC23],title='Train_ACC',flag='hidden')
plt.subplot(144)
ComPlot([test_ACC41,test_ACC42,test_ACC43,test_ACC23],title='Test_ACC', flag='hidden')
plt.show()

在本次实验中我对比了相同隐藏层数和不同隐藏神经元个数，以及不同隐藏层和不同隐藏神经元个数构成的前馈神经网络的效果。各种模型汇总如下：

Model	Hidden layer num	Each hidden num	time	ACC	Rank
model41	1	[128]	256.331s	0.853	2
model42	2	[512 256]	278.211s	0.854	1
model43	3	[512 256 108]	269.510s	0.852	3
model23	1	[256]	282.329s	0.851	4

从训练时间大致可以看出隐藏层数越多，隐藏神经元个数越多，所需要的时间越久。
从准确率来看，并不是隐藏层数越多，隐藏神经元个数越多，准确率越高，可能会有相反的效果。
更多的隐藏层和隐藏神经元个数，可能会导致模型的过拟合现象，导致在训练集上准确率很高，但在测试集上准确率很低（注：在本次实验中未能体现）

A1 实验心得

学会手动构建前馈神经网络和利用torch.nn构建前馈神经网络解决回归、二分类、和多分类问题

实验中发现学习率的设置至关重要，如果学习率过大则会导致准确率下降的趋势，若学习率过小会导致模型需要更多时间收敛
实验过程中发现出现过拟合现象，通过修改相关参数得以纠正
学会程序模块话的编写，避免重复编写代码
对激活函数的选取有了更加清晰的认识
隐藏层的个数和隐藏层的神经元个数对模型有着很大的影响。

你可能感兴趣的:(pytorch学习,深度学习,神经网络,深度学习)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
将cmd中命令输出保存为txt文本文件落难Coder Windows cmd window
最近深度学习本地的训练中我们常常要在命令行中运行自己的代码，无可厚非，我们有必要保存我们的炼丹结果，但是复制命令行输出到txt是非常麻烦的，其实Windows下的命令行为我们提供了相应的操作。其基本的调用格式就是：运行指令>输出到的文件名称或者具体保存路径测试下，我打开cmd并且ping一下百度：pingwww.baidu.com>./data.txt看下相同目录下data.txt的输出：如果你再
推荐3家毕业AI论文可五分钟一键生成！文末附免费教程！小猪包333 写论文人工智能 AI写作深度学习计算机视觉
在当前的学术研究和写作领域，AI论文生成器已经成为许多研究人员和学生的重要工具。这些工具不仅能够帮助用户快速生成高质量的论文内容，还能进行内容优化、查重和排版等操作。以下是三款值得推荐的AI论文生成器：千笔-AIPassPaper、懒人论文以及AIPaperPass。千笔-AIPassPaper千笔-AIPassPaper是一款基于深度学习和自然语言处理技术的AI写作助手，旨在帮助用户快速生成高质
AI大模型的架构演进与最新发展季风泯灭的季节 AI大模型应用技术二人工智能架构
随着深度学习的发展，AI大模型（LargeLanguageModels,LLMs）在自然语言处理、计算机视觉等领域取得了革命性的进展。本文将详细探讨AI大模型的架构演进，包括从Transformer的提出到GPT、BERT、T5等模型的历史演变，并探讨这些模型的技术细节及其在现代人工智能中的核心作用。一、基础模型介绍：Transformer的核心原理Transformer架构的背景在Transfo
ai绘画工具midjourney怎么下载？附作品管理教程设计师早上好
Midjourney是一款功能强大的AI绘画工具，它使用机器学习技术和深度神经网络等算法，可以生成各种艺术风格的绘画作品。在创意设计、广告宣传等方面有着广泛的应用前景。那么，ai绘画工具midjourney怎么下载？本文将为您介绍Midjourney的下载以及作品的相关管理。一、Midjourney下载Midjourney的下载非常简单，只需打开Midjourney官网（点击“GetMidjour
[实践应用] 深度学习之模型性能评估指标 YuanDaima2048 深度学习工具使用深度学习人工智能损失函数性能评估 pytorch python 机器学习
文章总览：YuanDaiMa2048博客文章总览深度学习之模型性能评估指标分类任务回归任务排序任务聚类任务生成任务其他介绍在机器学习和深度学习领域，评估模型性能是一项至关重要的任务。不同的学习任务需要不同的性能指标来衡量模型的有效性。以下是对一些常见任务及其相应的性能评估指标的详细解释和总结。分类任务分类任务是指模型需要将输入数据分配到预定义的类别或标签中。以下是分类任务中常用的性能指标：准确率(
[实践应用] 深度学习之优化器 YuanDaima2048 深度学习工具使用 pytorch 深度学习人工智能机器学习 python 优化器
文章总览：YuanDaiMa2048博客文章总览深度学习之优化器1.随机梯度下降（SGD）2.动量优化（Momentum）3.自适应梯度（Adagrad）4.自适应矩估计（Adam）5.RMSprop总结其他介绍在深度学习中，优化器用于更新模型的参数，以最小化损失函数。常见的优化函数有很多种，下面是几种主流的优化器及其特点、原理和PyTorch实现：1.随机梯度下降（SGD）原理:随机梯度下降通过
生成式地图制图 Bwywb_3 深度学习机器学习深度学习生成对抗网络
生成式地图制图（GenerativeCartography）是一种利用生成式算法和人工智能技术自动创建地图的技术。它结合了传统的地理信息系统（GIS）技术与现代生成模型（如深度学习、GANs等），能够根据输入的数据自动生成符合需求的地图。这种方法在城市规划、虚拟环境设计、游戏开发等多个领域具有应用前景。主要特点：自动化生成：通过算法和模型，系统能够根据输入的地理或空间数据自动生成地图，而无需人工逐
吴恩达深度学习笔记(30)-正则化的解释极客Array
正则化（Regularization）深度学习可能存在过拟合问题——高方差，有两个解决方法，一个是正则化，另一个是准备更多的数据，这是非常可靠的方法，但你可能无法时时刻刻准备足够多的训练数据或者获取更多数据的成本很高，但正则化通常有助于避免过拟合或减少你的网络误差。如果你怀疑神经网络过度拟合了数据，即存在高方差问题，那么最先想到的方法可能是正则化，另一个解决高方差的方法就是准备更多数据，这也是非常
个人学习笔记7-6：动手学深度学习pytorch版-李沐浪子L 深度学习深度学习笔记计算机视觉 python 人工智能神经网络 pytorch
#人工智能##深度学习##语义分割##计算机视觉##神经网络#计算机视觉13.11全卷积网络全卷积网络（fullyconvolutionalnetwork，FCN）采用卷积神经网络实现了从图像像素到像素类别的变换。引入l转置卷积（transposedconvolution）实现的，输出的类别预测与输入图像在像素级别上具有一一对应关系：通道维的输出即该位置对应像素的类别预测。13.11.1构造模型下
深度学习-点击率预估-研究论文2024-09-14速读 sp_fyf_2024 深度学习人工智能
深度学习-点击率预估-研究论文2024-09-14速读1.DeepTargetSessionInterestNetworkforClick-ThroughRatePredictionHZhong,JMa,XDuan,SGu,JYao-2024InternationalJointConferenceonNeuralNetworks,2024深度目标会话兴趣网络用于点击率预测摘要：这篇文章提出了一种新
计算机视觉中，Pooling的作用 Wils0nEdwards 计算机视觉人工智能
在计算机视觉中，Pooling（池化）是一种常见的操作，主要用于卷积神经网络（CNN）中。它通过对特征图进行下采样，减少数据的空间维度，同时保留重要的特征信息。Pooling的作用可以归纳为以下几个方面：1.降低计算复杂度与内存需求Pooling操作通过对特征图进行下采样，减少了特征图的空间分辨率（例如，高度和宽度）。这意味着网络需要处理的数据量会减少，从而降低了计算量和内存需求。这对大型神经网络
神经网络-损失函数红米煮粥神经网络人工智能深度学习
文章目录一、回归问题的损失函数1.均方误差（MeanSquaredError,MSE）2.平均绝对误差（MeanAbsoluteError,MAE）二、分类问题的损失函数1.0-1损失函数（Zero-OneLossFunction）2.交叉熵损失（Cross-EntropyLoss）3.合页损失（HingeLoss）三、总结在神经网络中，损失函数（LossFunction）扮演着至关重要的角色，它
损失函数与反向传播 Star_. PyTorch pytorch 深度学习 python
损失函数定义与作用损失函数(lossfunction)在深度学习领域是用来计算搭建模型预测的输出值和真实值之间的误差。1.损失函数越小越好2.计算实际输出与目标之间的差距3.为更新输出提供依据（反向传播)常见的损失函数回归常见的损失函数有：均方差（MeanSquaredError，MSE）、平均绝对误差（MeanAbsoluteErrorLoss，MAE）、HuberLoss是一种将MSE与MAE
BP神经网络的传递函数大胜归来19 MATLAB
BP网络一般都是用三层的，四层及以上的都比较少用；传输函数的选择，这个怎么说，假设你想预测的结果是几个固定值，如1,0等，满足某个条件输出1，不满足则0的话，首先想到的是hardlim函数，阈值型的，当然也可以考虑其他的；然后，假如网络是用来表达某种线性关系时，用purelin---线性传输函数；若是非线性关系的话，用别的非线性传递函数，多层网络时，每层不一定要用相同的传递函数，可以是三种配合，可
神经网络传递函数sigmoid,神经网络传递函数作用快乐的小荣荣神经网络机器学习深度学习人工智能
神经网络传递函数选取不同会有特别大差别嘛？只是最后一层，但前面层是非线性，那么可能存在区别不大的情况。线性函数f(a*input)=af(input),一般来说，input为向量，最简化情况下，可以假设input的各个维度，a1=a2=a3。。。意味着你线性层只是简单的对输入做了scale~而神经网络能起作用的原因，在于通过足够复杂的非线性函数，来模拟任何的分布。所以，神经网络必须要用非线性函数。
Python和R均方根误差平均绝对误差算法模型亚图跨际 Python 交叉知识 R 回归模型误差指标归一化均方根误差生态状态指标神经网络成本误差气体排放气候模型多项式拟合
要点回归模型误差评估指标归一化均方根误差生态状态指标神经网络成本误差计算气体排放气候算法模型Python误差指标均方根误差和平均绝对误差均方根偏差或均方根误差是两个密切相关且经常使用的度量值之一，用于衡量真实值或预测值与观测值或估计值之间的差异。估计器θ^\hat{\theta}θ^相对于估计参数θ\thetaθ的RMSD定义为均方误差的平方根：RMSD⁡(θ^)=MSE⁡(θ^)=E((θ^−θ
【深度学习】训练过程中一个OOM的问题，太难查了 weixin_40293999 深度学习深度学习人工智能
现象：各位大佬又遇到过ubuntu的这个问题么？现象是在训练过程中，ssh上不去了，能ping通，没死机，但是ubunutu的pc侧的显示器，鼠标啥都不好用了。只能重启。问题原因：OOM了95G，尼玛！！！！pytorch爆内存了，然后journald假死了，在journald被watchdog干掉之后，系统就崩溃了。这种规模的爆内存一般，即使被oomkill了，也要卡半天的，确实会这样，能不能配
云服务业界动态简报-20180128 Captain7
一、青云青云QingCloud推出深度学习平台DeepLearningonQingCloud，包含了主流的深度学习框架及数据科学工具包，通过QingCloudAppCenter一键部署交付，可以让算法工程师和数据科学家快速构建深度学习开发环境，将更多的精力放在模型和算法调优。二、腾讯云1.腾讯云正式发布腾讯专有云TCE(TencentCloudEnterprise)矩阵，涵盖企业版、大数据版、AI
机器学习VS深度学习 nfgo 机器学习
机器学习（MachineLearning,ML）和深度学习（DeepLearning,DL）是人工智能（AI）的两个子领域，它们有许多相似之处，但在技术实现和应用范围上也有显著区别。下面从几个方面对两者进行区分：1.概念层面机器学习：是让计算机通过算法从数据中自动学习和改进的技术。它依赖于手动设计的特征和数学模型来进行学习，常用的模型有决策树、支持向量机、线性回归等。深度学习：是机器学习的一个子领
大数据毕业设计hadoop+spark+hive知识图谱租房数据分析可视化大屏租房推荐系统 58同城租房爬虫房源推荐系统房价预测系统计算机毕业设计机器学习深度学习人工智能 2401_84572577 程序员大数据 hadoop 人工智能
做了那么多年开发，自学了很多门编程语言，我很明白学习资源对于学一门新语言的重要性，这些年也收藏了不少的Python干货，对我来说这些东西确实已经用不到了，但对于准备自学Python的人来说，或许它就是一个宝藏，可以给你省去很多的时间和精力。别在网上瞎学了，我最近也做了一些资源的更新，只要你是我的粉丝，这期福利你都可拿走。我先来介绍一下这些东西怎么用，文末抱走。（1）Python所有方向的学习路线（
深度学习-13-小语言模型之SmolLM的使用皮皮冰燃深度学习深度学习
文章附录1SmolLM概述1.1SmolLM简介1.2下载模型2运行2.1在CPU/GPU/多GPU上运行模型2.2使用torch.bfloat162.3通过位和字节的量化版本3应用示例4问题及解决4.1attention_mask和pad_token_id报错4.2max_new_tokens=205参考附录1SmolLM概述1.1SmolLM简介SmolLM是一系列尖端小型语言模型，提供三种规
【NLP5-RNN模型、LSTM模型和GRU模型】一蓑烟雨紫洛 nlp rnn lstm gru nlp
RNN模型、LSTM模型和GRU模型1、什么是RNN模型RNN（RecurrentNeuralNetwork)中文称为循环神经网络，它一般以序列数据为输入，通过网络内部的结构设计有效捕捉序列之间的关系特征，一般也是以序列形式进行输出RNN的循环机制使模型隐层上一时间步产生的结果，能够作为当下时间步输入的一部分（当下时间步的输入除了正常的输入外还包括上一步的隐层输出）对当下时间步的输出产生影响2、R
基于深度学习的农作物病害检测 SEU-WYL 深度学习dnn 深度学习人工智能
基于深度学习的农作物病害检测利用卷积神经网络（CNN）、生成对抗网络（GAN）、Transformer等深度学习技术，自动识别和分类农作物的病害，帮助农业工作者提高作物管理效率、减少损失。1.农作物病害检测的挑战病害种类繁多：农作物病害的类型多样，不同病害在同一作物上的表现差异很大，同时同一种病害在不同生长阶段的症状也可能不同。环境影响：天气、光照、湿度等外部环境因素会影响农作物的表现，使得病害检
基于深度学习的文本引导的图像编辑 SEU-WYL 深度学习dnn 深度学习人工智能
基于深度学习的文本引导的图像编辑（Text-GuidedImageEditing）是一种通过自然语言文本指令对图像进行编辑或修改的技术。它结合了图像生成和自然语言处理（NLP）的最新进展，使用户能够通过描述性文本对图像内容进行精确的调整和操控。1.文本引导的图像编辑的挑战文本和图像之间的对齐：如何将文本中的语义信息准确地映射到图像中的特定区域或元素是一个关键挑战。这涉及到多模态数据的对齐和理解。编
深度学习--对抗生成网络（GAN, Generative Adversarial Network） Ambition_LAO 深度学习生成对抗网络
对抗生成网络（GAN,GenerativeAdversarialNetwork）是一种深度学习模型，由IanGoodfellow等人在2014年提出。GAN主要用于生成数据，通过两个神经网络相互对抗，来生成以假乱真的新数据。以下是对GAN的详细阐述，包括其概念、作用、核心要点、实现过程、代码实现和适用场景。1.概念GAN由两个神经网络组成：生成器（Generator）和判别器（Discrimina
深度学习：怎么看pth文件的参数奥利给少年深度学习人工智能
.pth文件是PyTorch模型的权重文件，它通常包含了训练好的模型的参数。要查看或使用这个文件，你可以按照以下步骤操作：1.确保你有模型的定义你需要有创建这个.pth文件时所用的模型的代码。这意味着你需要有模型的类定义和架构。2.加载模型权重使用PyTorch的load_state_dict方法来加载权重。这里是如何操作的：importtorchimporttorch.nnasnn#定义模型结构
chatgpt赋能python：如何在Python中安装Keras库？ turensu ChatGpt python chatgpt keras 计算机
如何在Python中安装Keras库？Keras是一个简单易用的神经网络库，由FrançoisChollet编写。它在Python编程语言中实现了深度学习的功能，可以使您更轻松地构建和试验不同类型的神经网络。如果您是一名Python开发人员，肯定会想知道如何在您的Python项目中安装Keras库。在本文中，我们将向您展示如何安装和配置Keras库。步骤1：安装Python要使用Keras库，您需
如何理解深度学习的训练过程奋斗的草莓熊深度学习人工智能 python scikit-learn virtualenv numpy pandas
文章目录1.训练是干什么？2.预训练模型进行训练，主要更改的是预训练模型的什么东西？1.训练是干什么？以yolov5为例子，训练的目的是把一组输入猫狗图像放到神经网络中，得到一个输出模型，这个模型下次可以直接用来识别哪个是猫，哪个是狗2.预训练模型进行训练，主要更改的是预训练模型的什么东西？超参数（Hyperparameters）：这是模型结构中定义的参数，比如：卷积核大小（kernel_size
Keras深度学习框架入门及实战指南司莹嫣Maude
Keras深度学习框架入门及实战指南keraskeras-team/keras:是一个基于Python的深度学习库，它没有使用数据库。适合用于深度学习任务的开发和实现，特别是对于需要使用Python深度学习库的场景。特点是深度学习库、Python、无数据库。项目地址:https://gitcode.com/gh_mirrors/ke/keras一、项目介绍Keras简介Keras是一款高级神经网络
rust的指针作为函数返回值是直接传递，还是先销毁后创建？ wudixiaotie 返回值
这是我自己想到的问题，结果去知呼提问，还没等别人回答，我自己就想到方法实验了。。 fn main() { let mut a = 34; println!("a's addr:{:p}", &a); let p = &mut a; println!("p's addr:{:p}", &a
java编程思想 -- 数据的初始化百合不是茶 java 数据的初始化
1.使用构造器确保数据初始化 /* *在ReckInitDemo类中创建Reck的对象 */ public class ReckInitDemo { public static void main(String[] args) { //创建Reck对象 new Reck(); } }
[航天与宇宙]为什么发射和回收航天器有档期 comsci
地球的大气层中有一个时空屏蔽层,这个层次会不定时的出现,如果该时空屏蔽层出现,那么将导致外层空间进入的任何物体被摧毁,而从地面发射到太空的飞船也将被摧毁... 所以,航天发射和飞船回收都需要等待这个时空屏蔽层消失之后,再进行 &
linux下批量替换文件内容商人shang linux 替换
1、网络上现成的资料　　格式: sed -i "s/查找字段/替换字段/g" `grep 查找字段 -rl 路径` 　　linux sed 批量替换多个文件中的字符串　　sed -i "s/oldstring/newstring/g" `grep oldstring -rl yourdir` 　　例如：替换/home下所有文件中的www.admi
网页在线天气预报 oloz 天气预报
网页在线调用天气预报 <%@ page language="java" contentType="text/html; charset=utf-8" pageEncoding="utf-8"%> <!DOCTYPE html PUBLIC "-//W3C//DTD HTML 4.01 Transit
SpringMVC和Struts2比较杨白白 springMVC
1. 入口 spring mvc的入口是servlet，而struts2是filter（这里要指出，filter和servlet是不同的。以前认为filter是servlet的一种特殊），这样就导致了二者的机制不同，这里就牵涉到servlet和filter的区别了。参见：http://blog.csdn.net/zs15932616453/article/details/8832343 2
refuse copy, lazy girl! 小桔子 copy
妹妹坐船头啊啊啊啊！都打算一点点琢磨呢。文字编辑也写了基本功能了。。今天查资料，结果查到了人家写得完完整整的。我清楚的认识到： 1.那是我自己觉得写不出的高度 2.如果直接拿来用，很快就能解决问题 3.然后就是抄咩~~ 4.肿么可以这样子，都不想写了今儿个，留着作参考吧！拒绝大抄特抄，慢慢一点点写！
apache与php整合 aichenglong php apache web
一 apache web服务器 1 apeche web服务器的安装 1)下载Apache web服务器 2)配置域名(如果需要使用要在DNS上注册) 3)测试安装访问http://localhost/验证是否安装成功 2 apache管理 1)service.msc进行图形化管理 2)命令管理，配
Maven常用内置变量 AILIKES maven
Built-in properties ${basedir} represents the directory containing pom.xml ${version} equivalent to ${project.version} (deprecated: ${pom.version}) Pom/Project properties Al
java的类和对象百合不是茶 JAVA面向对象类对象
java中的类： java是面向对象的语言，解决问题的核心就是将问题看成是一个类，使用类来解决 java使用 class 类名来创建类，在Java中类名要求和构造方法，Java的文件名是一样的创建一个A类： class A{ } java中的类：将某两个事物有联系的属性包装在一个类中，再通
JS控制页面输入框为只读 bijian1013 JavaScript
在WEB应用开发当中，增、删除、改、查功能必不可少，为了减少以后维护的工作量，我们一般都只做一份页面，通过传入的参数控制其是新增、修改或者查看。而修改时需将待修改的信息从后台取到并显示出来，实际上就是查看的过程，唯一的区别是修改时，页面上所有的信息能修改，而查看页面上的信息不能修改。因此完全可以将其合并，但通过前端JS将查看页面的所有信息控制为只读，在信息量非常大时，就比较麻烦。
AngularJS与服务器交互 bijian1013 JavaScript AngularJS $http
对于AJAX应用（使用XMLHttpRequests）来说，向服务器发起请求的传统方式是：获取一个XMLHttpRequest对象的引用、发起请求、读取响应、检查状态码，最后处理服务端的响应。整个过程示例如下： var xmlhttp = new XMLHttpRequest(); xmlhttp.onreadystatechange
[Maven学习笔记八]Maven常用插件应用 bit1129 maven
常用插件及其用法位于：http://maven.apache.org/plugins/ 1. Jetty server plugin 2. Dependency copy plugin 3. Surefire Test plugin 4. Uber jar plugin 1. Jetty Pl
【Hive六】Hive用户自定义函数(UDF) bit1129 自定义函数
1. 什么是Hive UDF Hive是基于Hadoop中的MapReduce，提供HQL查询的数据仓库。Hive是一个很开放的系统，很多内容都支持用户定制，包括：文件格式：Text File，Sequence File 内存中的数据格式： Java Integer/String, Hadoop IntWritable/Text 用户提供的 map/reduce 脚本：不管什么
杀掉nginx进程后丢失nginx.pid，如何重新启动nginx ronin47 nginx 重启 pid丢失
nginx进程被意外关闭，使用nginx -s reload重启时报如下错误：nginx: [error] open() “/var/run/nginx.pid” failed (2: No such file or directory)这是因为nginx进程被杀死后pid丢失了，下一次再开启nginx -s reload时无法启动解决办法：nginx -s reload 只是用来告诉运行中的ng
UI设计中我们为什么需要设计动效 brotherlamp UI ui教程 ui视频 ui资料 ui自学
随着国际大品牌苹果和谷歌的引领，最近越来越多的国内公司开始关注动效设计了，越来越多的团队已经意识到动效在产品用户体验中的重要性了，更多的UI设计师们也开始投身动效设计领域。但是说到底，我们到底为什么需要动效设计？或者说我们到底需要什么样的动效？做动效设计也有段时间了，于是尝试用一些案例，从产品本身出发来说说我所思考的动效设计。一、加强体验舒适度嗯，就是让用户更加爽更加爽的用你的产品。
Spring中JdbcDaoSupport的DataSource注入问题 bylijinnan java spring
参考以下两篇文章： http://www.mkyong.com/spring/spring-jdbctemplate-jdbcdaosupport-examples/ http://stackoverflow.com/questions/4762229/spring-ldap-invoking-setter-methods-in-beans-configuration Sprin
数据库连接池的工作原理 chicony 数据库连接池
随着信息技术的高速发展与广泛应用，数据库技术在信息技术领域中的位置越来越重要，尤其是网络应用和电子商务的迅速发展，都需要数据库技术支持动态Web站点的运行，而传统的开发模式是：首先在主程序（如Servlet、Beans）中建立数据库连接；然后进行SQL操作，对数据库中的对象进行查询、修改和删除等操作；最后断开数据库连接。使用这种开发模式，对
java 关键字 CrazyMizzz java
关键字是事先定义的，有特别意义的标识符，有时又叫保留字。对于保留字，用户只能按照系统规定的方式使用，不能自行定义。 Java中的关键字按功能主要可以分为以下几类：（1）访问修饰符 public,private,protected p
Hive中的排序语法 daizj 排序 hive order by DISTRIBUTE BY sort by
Hive中的排序语法 2014.06.22 ORDER BY hive中的ORDER BY语句和关系数据库中的sql语法相似。他会对查询结果做全局排序，这意味着所有的数据会传送到一个Reduce任务上，这样会导致在大数量的情况下，花费大量时间。与数据库中 ORDER BY 的区别在于在hive.mapred.mode = strict模式下，必须指定 limit 否则执行会报错。
单态设计模式 dcj3sjt126com 设计模式
单例模式（Singleton）用于为一个类生成一个唯一的对象。最常用的地方是数据库连接。使用单例模式生成一个对象后，该对象可以被其它众多对象所使用。 <?phpclass Example{ // 保存类实例在此属性中 private static&
svn locked dcj3sjt126com Lock
post-commit hook failed (exit code 1) with output: svn: E155004: Working copy 'D:\xx\xxx' locked svn: E200031: sqlite: attempt to write a readonly database svn: E200031: sqlite: attempt to write a
ARM寄存器学习 e200702084 数据结构 C++c C#F#
无论是学习哪一种处理器，首先需要明确的就是这种处理器的寄存器以及工作模式。 ARM有37个寄存器，其中31个通用寄存器，6个状态寄存器。 1、不分组寄存器（R0-R7）不分组也就是说说，在所有的处理器模式下指的都时同一物理寄存器。在异常中断造成处理器模式切换时，由于不同的处理器模式使用一个名字相同的物理寄存器，就是
常用编码资料 gengzg 编码
List<UserInfo> list=GetUserS.GetUserList(11); String json=JSON.toJSONString(list); HashMap<Object,Object> hs=new HashMap<Object, Object>(); for(int i=0;i<10;i++) {
进程 vs. 线程 hongtoushizi 线程 linux 进程
我们介绍了多进程和多线程，这是实现多任务最常用的两种方式。现在，我们来讨论一下这两种方式的优缺点。首先，要实现多任务，通常我们会设计Master-Worker模式，Master负责分配任务，Worker负责执行任务，因此，多任务环境下，通常是一个Master，多个Worker。如果用多进程实现Master-Worker，主进程就是Master，其他进程就是Worker。如果用多线程实现
Linux定时Job：crontab -e 与 /etc/crontab 的区别 Josh_Persistence linux crontab
一、linux中的crotab中的指定的时间只有5个部分：* * * * * 分别表示：分钟，小时，日，月，星期，具体说来：第一段代表分钟 0—59 第二段代表小时 0—23 第三段代表日期 1—31 第四段代表月份 1—12 第五段代表星期几，0代表星期日 0—6 如： */1 * * * * 每分钟执行一次。 *
KMP算法详解 hm4123660 数据结构 C++算法字符串 KMP
字符串模式匹配我们相信大家都有遇过，然而我们也习惯用简单匹配法（即Brute-Force算法)，其基本思路就是一个个逐一对比下去，这也是我们大家熟知的方法，然而这种算法的效率并不高，但利于理解。假设主串s="ababcabcacbab",模式串为t="
枚举类型的单例模式 zhb8015 单例模式
E.编写一个包含单个元素的枚举类型[极推荐]。代码如下： public enum MaYun {himself; //定义一个枚举的元素，就代表MaYun的一个实例private String anotherField;MaYun() {//MaYun诞生要做的事情//这个方法也可以去掉。将构造时候需要做的事情放在instance赋值的时候：/** himself = MaYun() {*
Kafka+Storm+HDFS ssydxa219 storm
cd /myhome/usr/stormbin/storm nimbus &bin/storm supervisor &bin/storm ui &Kafka+Storm+HDFS整合实践kafka_2.9.2-0.8.1.1.tgzapache-storm-0.9.2-incubating.tar.gzKafka安装配置我们使用3台机器搭建Kafk
Java获取本地服务器的IP 中华好儿孙 java Web 获取服务器ip地址
System.out.println("getRequestURL:"+request.getRequestURL()); System.out.println("getLocalAddr:"+request.getLocalAddr()); System.out.println("getLocalPort:&quo