强化学习入门概念介绍

   最近偶然接触到了强化学习，折服于其强大的学习能力，遂找了一些论文和中文讲解看了一下，发现很多基础概念不管是中文还是英文都讲解得十分晦涩难懂，我费了很大的力气才终于理清了里面一些框架性的基础概念，这里挖坑对那些看上去晦涩的概念进行更通俗易懂地介绍，如有错误，欢迎指正。

1.强化学习的目的

   在学习过程中，最先困扰我的问题就是，强化学习到底学习了什么？答案是，强化学习主要是学习一种选择策略使得整个选择过程获得的回报最高。
   举个通俗的例子，比如我们在第十天需要参加考试，那么这考前的十天要怎么过才是最有意义或者说回报率最高呢？
这里又出现了一个问题，怎么定义有意义或者说回报率？对于这个具体问题，我们定义的意义或者回报就是心情愉悦程度：
1）如果玩十天，那么这十天肯定每天都很愉快，但最后考试肯定挂科，那这种策略下，我们的回报就是十天的好心情;
2）如果认真复习十天，那么这十天肯定每天都不愉快，回报率直接为负，但这种情况下可能就考试通过了，心情直接起飞，回报就是最后的心情愉悦程度减去复习的痛苦。
  强化学习的目的就是根据每个人的不同情况来作出这十天应该怎么过的策略。当然实际情况会比这个问题更为复杂，这里只是作个通俗易懂的说明。

2. 强化学习的结束标志

   前面给出了强化学习的目的是学习一种选择策略使得整个选择过程获得的回报最高，这里其实也出现了一个很难理解的概念“整个选择过程”，什么叫整个选择过程，选择过程到哪一步预示着结束？这里我们引入了终止状态这一概念，即当整个系统在某一选择策略下进入了终止状态，那么就算结束，我们累计从开始到终止状态的过程中获得的所有回报之和。
在上面的例子中，最终的考试结果就是终止状态。

3.强化学习的符号表示

   经过上面的介绍，我们已经对强化学习有了一个粗浅的认识，最起码知道了它是什么。下面就是怎么去找到这个最优策略以让整个过程回报最高了。此时就不是我们三言两语就能够描述的清楚的。为了能够广泛地利用这类算法更好地服务于生活，我们必须将问题抽象成一个可以用数学表示的模型，将回报最高化以精确地数学公式进行描述，求解。
   强化学习问题可以使用马尔科夫决策过程的框架进行定式化描述,包括状态,动作,决策和回报等。这里我们需要明确一个概念，马尔科夫决策过程是对强化学习问题的一种定式化描述，两者并不能划等号，事实上解决有模型的马尔科夫过程一般用DP（动态规划算法），只有在没有模型的马尔科夫过程决策中我们才使用RL（强化学习）。同样，强化学习的过程也不一定需要运用神经网络，基础的迭代算法也可以完成（其实将神经网络运用于强化学习是我一开始看强化学习的目的，我曾经甚至错误的理解强化学习就是用神经网络进行的某种学习而已，这里写出来也希望这种错误的想法不要再误导其他对强化学习有兴趣的人）。

3.1状态

   $S$表示环境状态集，这是一个有限集$S=\{s^1,s^2,...,s^N\}$，表示系统每一步决策之后会进入的不同状态，状态也分为中间状态和中止状态，系统的每一步决策都会进入到不同的状态，进入到终止状态以后，整个决策过程就结束了。这里我们用考前复习进行举例，我们第一天进行复习会进入一种状态，第一天不复习也会进入一种状态，往后每一天的复习和不复习都会对应不同的状态，这些都是中间状态，最后一天考试合格(或者不合格)就是一种终止状态，一旦进入终止状态，将不再进行决策。

3.2动作

   $A$表示动作集，这也是一个有限集$A=\{a^1,a^2,...,a^K\}$，动作可以用于控制系统的状态，一系列的动作集就可以使系统进入到一个特定的状态$A(s)$。这里我们用大家熟悉的贪吃蛇游戏进行举例，我们知道，贪吃蛇在一般情况下是可以进行向左、向右和向前进的，这里的向左、向右、向前进就对应了三个动作，而在每一个动作之后，贪吃蛇要么吃到了豆子，要么吃不到豆子，要么撞墙结束了游戏，这里的吃到了豆子，吃不到豆子，或者撞墙就对应了三种不同的状态，显而易见，我们可以通过一系列的向左、向右、向前等动作组合使得贪吃蛇达到吃不到豆子，吃到了一个豆子，吃到了两个豆子…撞到墙等等不同的状态。同样对于考前复习来说，复习和不复习都是系统可以选择的两个动作，而复习或不复习对应的知识掌握量就是系统的状态。

3.3状态转移函数

   在某一状态$s\in S$下进行某一动作$a\in A$后进入新的状态$s^{\prime }$的概率，定义为$T：S\times A\times S\to [0,1]$,即$T(s,a,s^{\prime })$,由定义可知$T(s,a,s^{\prime })\ge 0$且$T(s,a,s^{\prime })\le 1$，对于所有的状态和动作，我们有${\sum }_{s^{\prime }\in S}T(s,a,s^{\prime })=1$，$T$是一个对应于所有可能状态的概率分布，对于某一状态下的禁止动作，我们可以设置$T(s,a,s^{\prime })=0$，为了区分不同动作出现的顺序，我们定义一个离散的全局时钟$t=1,2,\mathrm{3...}$，此时$s_t$表示在时间$t$时的状态，$s_{t+1}$表示在时间$t+1$时的状态。只有对于完整的模型已知的马尔科夫决策过程才会存在状态转移函数，对于很多未知的模型，马尔科夫决策过程中并不存在状态转移函数。

3.4回报

   回报就是指在某一个状态或者在某一个状态做某一个动作能获得的好处，状态回报函数可以定义为$R:S\to \mathbb{R}$，描述了在某一状态下能获得的回报，当然我们也可以定义状态-动作回报函数$R:S\times A\to \mathbb{R}$，表示在某状态下进行某动作能获得的回报，同样我们可以定义状态转移回报函数$R:S\times A\times S\to \mathbb{R}$，表示从某状态进行某动作后转移到另一状态的回报。回报函数是马尔科夫决策过程的一个重要要素，它规定了决策的目标，即回报最大化。

3.5策略

   给出了一个马尔科夫决策过程，我们就需要寻找到一个策略$\pi$，用它可以计算出对于某一个状态$s\in S$应作出的动作$a\in A$，一般定义为$\pi :S\to A$。将一个策略用于一个马尔科夫决策过程的方法如下：首先是进入起始状态$s_0$，在该状态下运用策略$\pi$获得该状态下的动作$a_0=\pi (s_0)$并执行，使得状态转移到$s_1$，根据状态转移函数和回报函数计算出从$s_0$到$s_1$的状态转移概率$T(s_0,a_0,s_1)$ 和回报$r_0=R(s_0,a_0,s_1)$，继续这个过程获得一系列的$s_0,a_0,r_0,s_1,a_1,r_1,s_2,a_2...$。如果这个过程不是持续性的，那么将会在终止状态结束并重新开始，如果这个过程是连续性的，那么该过程会一直持续下去。这里大家可能会有疑问，即状态转移概率的作用是什么，如果策略能够决定下一步的动作，似乎状态转移概率就可有可无了，事实并非如此，状态转移函数只是对于已知模型的马尔科夫决策过程存在，它决定了当系统处于当前状态时，进入后面不同状态的概率，而策略正是我们需要求解的，系统会由于我们选择了不同的行动而进入不同的状态。

3.6优化准则

   通过前面的符号介绍，相信大家对马尔科夫决策过程的各个要素已经有了充分的了解了，那么强化学习到底优化的是这里面的哪个要素呢？答案是累积回报，我们通过尝试不同的策略改变整个过程的累积回报，累积回报最大化对应着最优策略，而寻找最优的策略就是解马尔科夫决策过程。这里我们对累计回报（优化准则）进行说明，从字面意思就可以发现，累积回报不是某一个或某几个状态下的回报，而是对整个决策过程的回报进行累加，那么对于有限次的决策过程，累积回报就可以定义为
$$E[\sum _{t=0}^h{r}_t]$$
但是很多时候决策过程的终止并不是我们可以预见的，比如贪吃蛇游戏，如果蛇头不撞上墙壁或自己，游戏是可以一直继续的，此时我们定义了另一种累积回报函数
$$E[\sum _{t=1}^{\infty }{\gamma }^t{r}_t]$$
其中$\gamma$是损失参数，在0和1之间，即回报分为当前即时回报和未来回报，未来的回报对现在的回报累积产生影响，但是影响会随着时间的增加而减小，减小率就是$\gamma$，这个累积回报也是我们多数情况下所使用的。

4.价值函数和贝尔曼方程

   在前面的小节中我们介绍了马尔科夫决策过程和优化准则，在这一节中我们将探讨怎么去寻找这个优化策略使得整个决策过程的累积回报最大化。首先我们来定义价值函数，这其实是累积回报的另一种表达方式，即最大化价值函数等于累积回报最大化，对应的策略即是我们搜寻的策略。这里我们采用上面优化准则的第二个公式定义价值函数，即在状态$s$时，采用策略$\pi$对应的价值函数定义为以状态$s$为起始状态，在策略$\pi$ 下获得的累积回报的数学期望：
$$V^{\pi }(s)=E_{\pi }\{\sum _{k=0}^{\infty }{\gamma }^k{r}_{t+k}|s_t=s\}\text{\hspace{1em}(1)}$$
价值函数的一个基本特征就是其满足特定的递归属性，由于该属性，我们可以从价值函数中分解出贝尔曼方程因子：
$$\begin{array}{rl}{V}^{\pi }(s)& =E_{\pi }\{\sum _{k=0}^{\infty }{\gamma }^k{r}_{t+k}|s_t=s\}\\ & =E_{\pi }\{r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+...|s_t=t\}\\ & =E_{\pi }\{r_t+\gamma V^{\pi }(s_{t+1})|s_t=s\}\\ & =\sum _{s^{\prime }}T(s,\pi (s),s^{\prime })(R(s,a,s^{\prime })+\gamma V^{\pi }(s^{\prime }))\end{array}\text{\hspace{1em}(2)}$$
其中$T(s,\pi (s),s^{\prime })$表示从状态$s$转换到$s^{\prime }$的状态转换概率，我们知道从$s$转换到下一个状态有多种可能，每种可能状态对应的累积回报乘以该种状态出现的概率即为当前状态下累积回报对应的数学期望，值得注意的是，多种决策可能会获得同一个价值，但是每一个决策对应的价值函数$V^{\pi }$是固定的。
马尔可夫决策过程的目标是选出最优的策略使得整个过程的价值最高，即最优策略$V^{\ast }=V^{{\pi }^{\ast }}$满足：
$$V^{\ast }(s)=\underset{a\in A}{\max }\sum _{s^{\prime }\in S}T(s,a,s^{\prime })(R(s,a,s^{\prime })+\gamma V^{\ast }(s^{\prime }))\text{\hspace{1em}(3)}$$
这个就叫做贝尔曼优化等式，这其实在我看来是一个套娃定义，因为我们在计算$V^{\ast }(s)$时，竟然需要用到下一个状态的最大价值$V^{\ast }(s^{\prime })$，就意味着我已经知道了最优策略${\pi }^{\ast }$，但是如果我已经知道了最优策略${\pi }^{\ast }$，那我又还有什么必要去求解$V^{\ast }(s)$呢。这里先按住不表，我们只需要知道一点，就是前后两个状态的价值函数必须要满足等式3，即贝尔曼优化等式，也即在一个优化策略的作用下某一状态的价值必须等于该状态下最佳动作对应的数学期望。那么在给出优化状态价值函数$V^{\ast }$的情况下，我们可以通过以下公式计算出该状态下的最优动作：
$${\pi }^{\ast }(s)=\underset{a}{\mathrm{argmax}}\sum _{s^{\prime }\in S}T(s,a,s^{\prime })(R(s,a,s^{\prime })+\gamma V^{\ast }(s^{\prime }))\text{\hspace{1em}(14)}$$
相似地，这里我们可以定义出一个状态-动作价值函数:
$$Q^{\ast }(s,a)=\sum _{s^{\prime }}T(s,a,s^{\prime })(R(s,a,s^{\prime })+\gamma \underset{a^{\prime }}{\max }{Q}^{\ast }(s^{\prime },a^{\prime }))\text{\hspace{1em}(4)}$$
叫做$Q$-函数，它与$V$函数的关系是：
$$\begin{gathered} Q^{\ast }(s,a)=\sum _{s^{\prime }\in S}T(s,a,s^{\prime })(R(s,a,s^{\prime })+\gamma V^{\ast }(s^{\prime })) \\ {V}^{\ast }(s)=\underset{a}{\max }{Q}^{\ast }(s,a)\text{\hspace{1em}(5)} \end{gathered}$$
从而我们知道
$${\pi }^{\ast }(s)=\underset{a}{\mathrm{argmax}}{Q}^{\ast }(s,a)\text{\hspace{1em}(6)}$$
即最优动作就是该动作会使得该状态下的价值函数的数学期望最大。

5.解马尔科夫决策过程（MDP）

   现在我们已经介绍完MDP的定义，策略，优化准则以及价值函数等一系列要素了，解一个给定的MDP就是计算出最优的策略${\pi }^{\ast }$。为此存在多种算法，明显的区别就是model-based 和model-free算法。model-based算法大体上主要叫做DP算法，主要是假设MDP模型已知，并且可以使用贝尔曼等式来计算价值函数和策略，通过计算当前模型下的状态价值函数来选择最优动作。model-free算法大体上主要叫做RL算法，该算法不需要提前知道一个完美的模型，主要依赖于和环境的互动。
   一个基本原理就是生成策略迭代原理GPI（generalized policy iteration），该原理包括两个迭代过程。首先是策略评估过程，计算$V^{\pi }$来评估当前策略的价值。在model-based算法里，我们可以使用模型来直接计算或者迭代逼近，在model-free模型里面，我们可模拟策略并且根据选出的执行轨迹来评估该策略的价值，主要目的就是收集策略的信息以完成第二步的策略改进。在第二步策略改进过程中，我们通过计算每一个动作对应的价值来寻求策略改进的可能性，例如在当前状态下执行其他的动作可能比延续一直的策略获得的价值更大。这一步骤以原先的策略$\pi$为基础通过使用$V^{\pi }$计算出一个更优的策略${\pi }^{\prime }$。不管是策略评估还是策略改进都可以通过不同的方法完成。下图显示了该原理的示意图，底部的线表示一个推动整个价值学习过程的策略，它决定了价值函数，但是也同时存在另一个价值函数被策略用于选择动作。需要注意的是也可能存在一个隐含的策略，此时只有价值函数，策略只是在被需要的时候被计算出来，这就是所谓的model-free 算法。相应的同样存在隐藏的价值函数。另一个值得关注的是价值函数有时候并不需要太过精确，只要能区分次优动作和最优动作即可，只要不影响优化策略的选择即可。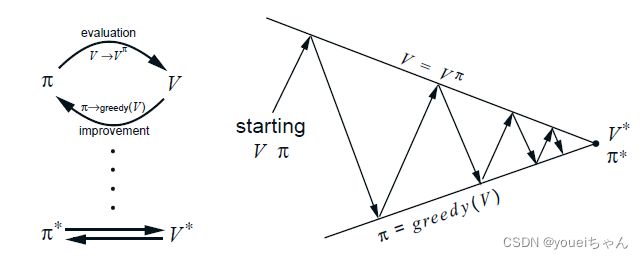

5.1model-based 算法：动态规划（DP）

   $DP$指的是在完全知道环境模型的情况下进行优化策略计算的一类算法，现实中往往我们很难对一个环境有十分的把握，但是从理论或者说算法的角度来讲，$DP$算法的计算机制其实是和model-free算法的计算机制是有关联的。这里我们假设一个标准的$MDP<S,A,T,R>$模型,状态和动作都是有限且离散的，同时，状态转换函数，回报以及价值方程也是一一记录的。两个主要的动态规划算法就是策略迭代和价值迭代，下面我们将逐个进行介绍。

5.1.1策略迭代算法

   策略迭代算法是在GPI（generalized policy iteration）的两个步骤策略评估和策略改进之间进行迭代，策略评估阶段计算出当前策略的价值函数，策略改进阶段计算一个优化策略使其能够最大化价值函数，不断地重复上述过程直至收敛到一个优化策略。

5.1.2策略评估

   策略评估首先需要寻求一个固定策略$\pi$的价值函数$V^{\pi }$，这是计算优化策略过程中的重要一环，从上面的介绍已知，对于所有的状态$s\in S$，我们有：
$$\begin{array}{r}{V}^{\pi }(s)=\sum _{s^{\prime }\in S}T(s,\pi (s),s^{\prime })(R(s,\pi (s),s^{\prime })+\gamma V^{\pi }(s^{\prime }))\end{array}\text{\hspace{1em}(7)}$$
如果整个系统的动态是已知的，MDP模型已经给定，那么这些方程就组成了有$|S|$个方程$|S|$个未知数的系统（未知数为每一个状态$s$对应的价值函数$V^{\pi }(s)$），这就可以通过解线性方程获得。同样，我们也可以用迭代的方法进行求解，这里我们考虑将贝尔曼等式转换为迭代更新公式，我们将当前状态大价值函数记为$V_k^{\pi }$，而在当前状态下前进一步记为$V_{k+1}^{\pi }$，此时：
$$\begin{array}{rl}{V}_{k+1}^{\pi }(s)& =E_{\pi }\{r_t+\gamma V_k^{\pi }(s_{t+1})|s_t=s\}\\ & =\sum _{s^{\prime }\in S}T(s,\pi (s),s^{\prime })(R(s,\pi (s),s^{\prime })+\gamma V_k^{\pi }(s^{\prime }))\end{array}\text{\hspace{1em}(8)}$$
$V_k^{\pi }$序列随着$k$的增加将会收敛。为了能够收敛，在每一次迭代时，我们都将该迭代公式用于状态集中的所有状态。算法使用新值替换旧值，是完全后向的算法。还有一种更加普遍的定义，我们定义后向算子$B^{\pi }$，对于每一个状态$s$对应的实值函数$\phi$进行后向运算：
$$(B^{\pi }\phi )(s)=\sum _{s^{\prime }\in S}T(s,\pi (s),s^{\prime })(R(s,\pi (s),s^{\prime })+\gamma \phi (s^{\prime }))\text{\hspace{1em}(9)}$$
某一个策略的价值函数$V^{\pi }$满足该后向算子的固定点$V^{\pi }=B^{\pi }{V}^{\pi }$（即，迭代进行到最后时$V^{\pi }$收敛到一个固定的值，将不再进行更新）。同样，我们可以定义某一动作$a$对应的后向算子:
$$(B^a\phi )(s)=R(s)+\gamma \sum _{s^{\prime }\in S}T(s,a,s^{\prime })\phi (s^{\prime })\text{\hspace{1em}(10)}$$

5.1.3策略改进

   经过策略评估阶段，我们已经知道了策略$\pi$对应的价值函数$V^{\pi }$，接下来就是改进该策略，首先我们定义对于动作$a$的价值：
$$\begin{array}{rl}{Q}^{\pi }(s,a)& =E_{\pi }\{r_t+\gamma V^{\pi }(s_{t+1})|s_t=s,a_t=a\}\\ & =\sum _{s^{\prime }}T(s,a,s^{\prime })(R(s,a,s^{\prime })+\gamma V^{\pi }(s^{\prime }))\end{array}\text{\hspace{1em}(11)}$$
如果$Q^{\pi }(s,a)$对于某些动作$a$的值大于$V^{\pi }(s)$，那么在该状态下选择动作$a$将会比当前策略选择的动作$\pi (s)$好。换句话说，此时我们可以通过在一个特定的状态选择另一个更加有价值的动作来优化当前的策略。事实上，我们可以在所有的状态评估所有的动作来获得该状态下的最有价值的动作，即我们可以基于当前的价值函数$V^{\pi }$计算出每一个状态的最有价值动作，从而得出一个贪婪策略${\pi }^{\prime }$：
$$\begin{array}{rl}{\pi }^{\prime }(s)& =\underset{a}{\mathrm{argmax}}{Q}^{\pi }(s,a)\\ & =\underset{a}{\mathrm{argmax}}E\{r_t+\gamma V^{\pi }(s_{t+1})|s_t=s,a_t=a\}\\ & =\underset{a}{\mathrm{argmax}}\sum _{s^{\prime }}T(s,a,s^{\prime })(R(s,a,s^{\prime })+\gamma V^{\pi }(s^{\prime }))\end{array}\text{\hspace{1em}(12)}$$
策略改进就是通过贪婪政策选择最佳动作使得对应于原选择策略的价值函数获得最大值，如果策略不能再优化了说明该策略已经是最优的了。总得来说，策略迭代以一个随机策略${\pi }_0$初始化，然后经过一系列的迭代，对策略进行评估与改进。策略评估阶段计算出$V^{{\pi }_k}$，利用公式8进行迭代。第二步根据获得的$V^{{\pi }_k}$从${\pi }_k$计算优化策略${\pi }_{k+1}$，对于每一个状态计算该状态下的最优动作，如果对于每一个状态，我们有${\pi }_{k+1}(s)={\pi }_k(s)$，那么说明策略已经稳定，可以停止策略迭代过程。策略迭代过程生成了一系列的策略和价值函数：
$${\pi }_0\to V^{{\pi }_0}\to {\pi }_1\to V^{{\pi }_1}\to {\pi }_2\to V^{{\pi }_2}\to {\pi }_3\to V^{{\pi }_3}\to ...\to {\pi }^{\ast }$$
整体的算法流程入下图所示：

对于有限的MDPs过程，状态和动作都是有限的，每一个${\pi }_{k+1}$都优于${\pi }_k$，除非${\pi }_k={\pi }^{\ast }$。同样由于是有限的MDP过程，策略可以在有限的时间内收敛，通常在几次迭代以后就会收敛。尽管策略会收敛，但是该算法的效率还是不高的，尤其是在第一步进行策略评估时，会消耗很多的计算资源。

5.1.2价值迭代算法

   策略迭代算法将策略评估和策略更新两个过程完全分离了，在策略评估过程中，价值函数必须被完全计算出来（满足迭代收敛条件），事实上，我们并不需要等待价值函数计算过程完全收敛，我们可以提前结束迭代过程并且利用当前的价值函数进行策略改进，迭代提前截断的极值点就是价值迭代算法，它可以在一次迭代以后直接中止策略评估过程。事实上这就是将策略改进过程融入到了策略评估过程中，因此该算法更加直接地关注价值函数的估算，此时我们重新定义策略改进更新规则：
$$\begin{array}{rl}{V}_{t+1}(s)& =\underset{a}{\max }\sum _{s^{\prime }}T(s,a,s^{\prime })(R(s,a,s^{\prime })+\gamma V_t(s^{\prime }))\\ & =\underset{a}{\max }{Q}_{t+1}(s,a)\end{array}\text{\hspace{1em}(13)}$$
使用公式13，价值更新算法可如下进行：从任意价值函数$V_0$开始，根据公式13更新每一个状态的价值函数得到下一个迭代循环的价值函数$V_t(t=1,2,3,...)$，该算法得到如下的价值函数序列：
$$V_0\to V_1\to V_2\to V_3\to V_4\to V_5\to V_6\to V_7\to ...V^{\ast }$$
当然，在计算价值函数的过程中，我们也可以同时计算出$Q$值，即：
$$V_0\to Q_1\to V_1\to Q_2\to V_2\to Q_3\to V_3\to Q_4\to V_4\to ...V^{\ast }$$
价值迭代会趋向于$V^{\ast }$收敛，利用方程14我们可以计算出所有状态$s\in S$的策略$\pi$。如果我们使用前面相似的后向算子，我们可以用如下的方式定义价值迭代过程：
$$(B^{\prime }\phi )(s)=\underset{a}{\max }\sum _{s^{\prime }\in S}T(s,a,s^{\prime })\{R(s,a,s^{\prime })+\gamma \phi (s^{\prime })\}\text{\hspace{1em}(15)}$$
该后向算子就像是价值函数的一个收缩映射，如果我们假设${\pi }^{\ast }$是优化策略，$V^{\ast }$是它的价值函数，那么我们就有$V^{\ast }=B^{\ast }{V}^{\ast }$，这里$(B^{\ast }V)(s)={\max }_a(B^{a}V)(s)$，如果我们定义$Q^{\ast }(s,a)=B^a{V}^{\ast }$,那么我们就有${\pi }^{\ast }(s)={\pi }_{greedy}(V^{\ast })(s)={\mathrm{argmax}}_a{Q}^{\ast }(s,a)$。说了这么多，其实总的概括起来就是，该算法以任意的价值函数$V^0$初始化，通过$V_{t+1}=B^{\ast }{V}^t$进行迭代，直到$\Vert V_{t+1}-V_t\Vert s<\epsilon$，即，直到价值函数的值更新量足够小为止。
下图为价值迭代的流程图：

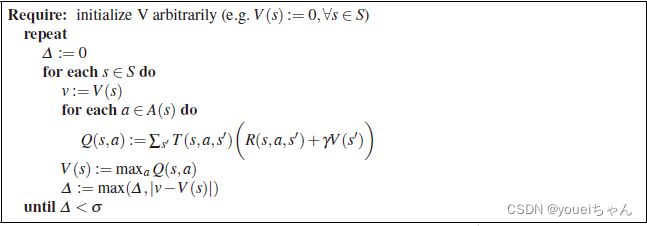
5.2 model-free算法：强化学习

   前面介绍了解决MDP问题时假设模型已知的算法，这一节我们将介绍没有模型的情况下如何去获得优化决策，即所谓的强化学习，不同于前面的算法，强化学习的过程中不存在已知的状态转化函数和回报等。由于这些要素的缺失，算法必须能够进行MDP过程取样以获取该未知模型的一些统计学信息。大多数无模型的强化学习通过动作来探知环境，估算状态价值或者状态-动作价值。
   在model-free算法中，我们仍有两种不同的做法，一种是首先通过和环境的互动来学习状态转换函数和回报，然后当模型相对准确时再运用前面章节介绍的动态规划DP模型进行求解最优策略，这种方式叫做间接强化学习。第二种选择就是直接强化学习，不对模型进行任何的预测而直接估算动作价值函数。当然我们也可以两种算法兼而有之，即在直接估测动作价值函数的过程中利用大概不太准确的模型去加速这个算法的收敛速度。大多数的model-free算法是直接进行动作价值估算的。
   另一个选择是如何做时间信任分配。我们知道评估一个动作的有效性是很难的，特别是当这个动作的作用要在其后面很久才显现出来的时候。一个可能的做法是直到整个过程结束再对某些特定的动作进行惩罚或者是奖励。但是，这将会占用很大的内存而且对于持续进行的任务，我们很难判定其在哪里或者在什么时候结束。此时，就存在了另一种做法，它的基本运行机制和价值迭代算法相似，某一个状态的价值等于其本身的即使回报加上下一个状态的回报的一部分，这叫做时间差学习法，是本小节中主要使用的方法。和DP算法的主要不同点是在RL算法的更新准则里将不能再使用状态转换函数$T$和回报$R$。与环境互动并在每一次循环后进行更新的算法被叫做在线学习法。一个经典的在线学习法如下图所示：

该图显示了一个互动循环，代理基于当前的状态选择了一个动作$a$，进入下一个状态$s^{\prime }$，并获得回报$r$，然后更新估计的$\tilde{V}$和$\tilde{Q}$的值以及$\tilde{T}$和$\tilde{R}$相关的统计数据的值(对于一些间接学习过程)。动作的选择是基于当前的状态$s$和价值函数$Q$或者$V$的。为了解决探索-开发问题，我们通常使用一个分离的探索机制来保证在某些情况下选择最佳动作（根据当前的动作价值选择，所谓的开发过程）某些情况下选择其他的动作（探索）过程，探索过程存在多种的选择，从随机到复杂都可以。

5.2.1探索过程

   model-free算法的一个重要特征就是需要探索过程，由于模型的未知性，算法必须要去尝试其他的动作来观察其结果，它需要在探索和开发之间维持一个平衡，即为了获得更多的回报，该算法在必须通过已知的信息开发最佳动作的同时还应该尝试其他的动作来探索环境以获得更好的回报。最基础的探索策略是$\epsilon$-贪婪策略，即算法在当前状态下执行最优动作的概率是$(1-\epsilon )$，执行其他动作的概率是$\epsilon$。还有许多其他的做法来实现环境探索，下面我们以玻尔兹曼探索策略为例进行介绍，它稍复杂于$\epsilon$-贪婪策略，此时的动作选择仍然是随机的，但是动作选择的概率和它们相对应的$Q$值相关，这使得系统更倾向于选择好的动作，当两个动作对应的$Q$值相同时，它们被选择的概率也相同，一般定义如下：
$$P(a_n)=\frac{e^{\frac{Q(s,a)}{T}}}{{\sum }_{i}e\frac{Q(s,a_i)}{T}}\text{\hspace{1em}(16)}$$
其中$P(a_n)$是选择动作$a_n$的概率，$T$是温度参数，较高的$T$值会使得选择过程趋向于随机策略，较低的$T$值会是的选择过程趋向于贪婪策略。当然我们也可以将$\epsilon$-贪婪策略和玻尔兹曼探索策略相结合，最佳动作的选择概率使用$(1-\epsilon )$，其他动作的选择概率根据公式16计算。
还有一种简单的探索方法就是优化$Q$-值的初始化，在学习开始的时候，我们可以用一个相对较大的值来初始化$Q$-值，比如一个事先定义好的上限值。由于$Q$-值在学习的过程中会不断地减小，因而那些没被采取的动作的$Q$-值将会大于一些已经执行过的动作，根据公式16，它们就会有比较高的概率被选择。还有一种做法就是设置一个计数器，记录每一个动作被执行的次数。

5.2.2 时间差异学习(TD learning)

   TD learning算法是基于一些估定值来预估某些值。这里可能比较抽象，我们使用一个日常生活的例子来解释。假设你请客吃饭，你必须要提前告诉你的客人几点到达你家。在你进行烹饪之前，你必须先去超市再去肉店和酒屋来买你招待客人所需的食材和酒水，你预估去肉店和酒屋可以在十分钟之内完成，而去超市需要半个小时，预计晚上六点前可以回来，那么你就可以告诉客人在六点以后来你家。但是当你去肉店和酒屋时，你发现道路非常拥挤，原定的十分钟生生被拖到了三十分钟，那么你此时可以预测你到家的时间将比原先预测的晚20分钟，而你去超市以后发现只用十分钟就买好了所有的东西，此时你可以进一步更新你的预测，你将可以准时到家。从这个例子我们可以看出，当你经历过程中的一部分时，你可以随时地调整你的预测结果而不需要等到整个过程结束，这就是TD learning的一个主要原理。

5.2.3 TD(0)

   TD(0)是TD learning算法的一种，它以在线和递增的方式估计一些策略$\pi$的价值函数$V^{\pi }$。TD(0)使用下面的更新规则：$$V_{k+1}(s):=V_k(s)+\alpha (r+\gamma V_k(s^{\prime })-V_k(s))$$
其中$\alpha \in [0,1]$ 是学习率，决定了该值的更新幅度，表示在系统执行动作$a$后，由状态$s$进入到状态$s^{\prime }$，同时获得回报$r$,它与DP不同的是该算法的更新只考虑一个成功转换的状态的价值而不是所有可能转换状态价值的数学期望。学习率$\alpha$可以随着学习过程的收敛而减小，同时也可以对不同的状态定义不同的学习率$\alpha (s)$这依赖于该状态被访问的频率。

5.2.4 Q-learning

   终于写到了强化学习最常用到的Q-learning算法了，它也是一直model-free类的学习算法，用于估算Q值函数。Q-learning的基本思想是基于系统的反馈逐步估计各个动作的Q值。更新规则是TD(0)算法更新规则的变形，用Q值以及一个内置的最大取值运算来将$Q_t$更新为$Q_{t+1}$：
$$Q_{k+1}(s_t,a_t)=Q_k(s_t,a_t)+\alpha (r_t+\gamma \underset{a}{\max }{Q}_k(s_{t+1},a)-Q_k(s_t,a_t))\text{\hspace{1em}(17)}$$
通过代理与环境的一次互动$a_t$，将状态由$s_t$更新到$s_{t+1}$，并获得回报$r_t$。Q-learning算法是探索迟钝型算法，它只会收敛到最优策略。算法过程如下图所示：

5.2.5 SARSA 算法

   Q-learning算法是个没有策略的算法，这就意味着尽管存在探索策略$\pi$，算法最终也是收敛到优化策略${\pi }^{\ast }$。与此不同的是SARSA算法是一个有策略的算法，它是基于探索策略$\pi$进行Q值学习的，迭代更新规则为：
$$Q_{k+1}(s_t,a_t)=Q_k(s_t,a_t)+\alpha (r_t+\gamma Q_k(s_{t+1},a_{t+1})-Q_k(s_t,a_t))\text{\hspace{1em}(18)}$$这里的动作$a_{t+1}$就是当前策略基于状态$s$作出的动作选择。这里的最大化取值被基于更新策略的动作-状态的Q值所取代。值得注意的是在所有的状态和动作都被无限次重复时，该算法仍然收敛到价值函数的最优解，策略也将收敛到贪婪策略，此时探索还是不会出现。SARSA算法在非稳定环境中非常有用，因为在这种状态下我们几乎不可能获得一个最优策略，同样该算法在函数近似中也很有用，因为在这种情况下无策略算法往往会出现分歧。当然无策略算法在很多其他的情况下也是特别有用的。

5.2.6 Actor-Critic learning算法

   在Q-learning算法和SARSA算法之前，还有一种有策略的学习算法叫做Actor-Critic learning，该算法是TD算法一族，保存了独立于价值函数的策略。策略被叫做actor，而价值函数就是critic。critic通过TD-误差评估actor产生的动作的价值，TD-误差的定义如下：
$${\delta }_t=r_t+\gamma V(s_{t+1})-V(s_t)$$该误差的目的是为了增强或者削弱某一状态下某个动作的选择，一个倾向于该动作的选择参数我们定义为$p(s,a)$:
$$p(s_t,a_t):=p(s_t,a_t)+\beta {\delta }_t$$这里的参数$\beta$控制了更新幅度。同样存在其他类的 Actor-Critic learning算法，主要的不同就是动作选择倾向的改变，即上面的公式。拥有独立策略的好处就是如果存在很多的动作供选择或者动作空间是连续的情况下，我们不需要考虑全部的动作。其次是它可以自然地学习随机策略，此外关于策略的先验知识也可以被使用。

5.3 总结

   至此，我们介绍完了一些基本的求解马尔科夫过程优化策略的算法，主要包括model-based的DP类算法和model-free的RL类算法。随着深度学习的发展，很多学者们也探索出了将深度学习运用于强化学习（RL）过程的算法，那么如何将神经网络运用到强化学习的过程中呢？这里我们对利用神经网络进行Q值学习进行简单的介绍。
神经网络在强化学习的过程中一般扮演的是策略选择的角色，即当前系统处于某状态时，我们将该状态对应的参数作为神经网络的输入，而网络的输出就是在该状态下我们采取不同的行动对应的Q值，按照贪婪策略，我们选择Q值最大的行动。那么如何对这个策略选择网络进行训练呢？这里的loss函数定义与Q-learning算法相似：
$$Q_{k+1}(s_t,a_t)=Q_k(s_t,a_t)+\alpha (r_t+\gamma \underset{a}{\max }{Q}_k(s_{t+1},a)-Q_k(s_t,a_t))$$
经过多次迭代后，当$Q_{k+1}(s_t,a_t)-Q_k(s_t,a_t)<\epsilon$时，我们就停止迭代，获得系统的最优决策，故而：
$$loss=Q_{k+1}(s_t,a_t)-Q_k(s_t,a_t)-\alpha (r_t+\gamma \underset{a}{\max }{Q}_k(s_{t+1},a)-Q_k(s_t,a_t))$$
根据$loss$函数的值不断地调整网络参数降低$loss$，最后在$loss$足够小的时候，我们获得整个系统的最优策略选择器。当然我们也可以定义另一个网络来计算$Q_k(s_{t+1},a)$，此时就是有策略的训练过程，但是这并不影响最终的算法收敛到贪婪策略。