数据结构：五岔路口交通灯问题

数据结构：五岔路口交通灯问题

网上有很多关于这个问题的文章，但是基本都是用的贪心算法，贪心算法的思路比较简单，而且时间复杂度是多项式级别的，但是贪心算法得到的最终结果并不能保证是最优解。所以，这里我写一下关于这个问题的穷举法解法，顺便也把贪心算法的代码贴一下。

交通指挥灯问题。一个具有五条通路的交叉路口，当允许某些通路上的车辆在交叉路口通行时，必须对其他通路上的车辆加以限制，不许同时在交叉路口通行，以免发生碰撞。
问题：如何依题意建立一个可以求解不同颜色灯的数量来指挥交通的模型？

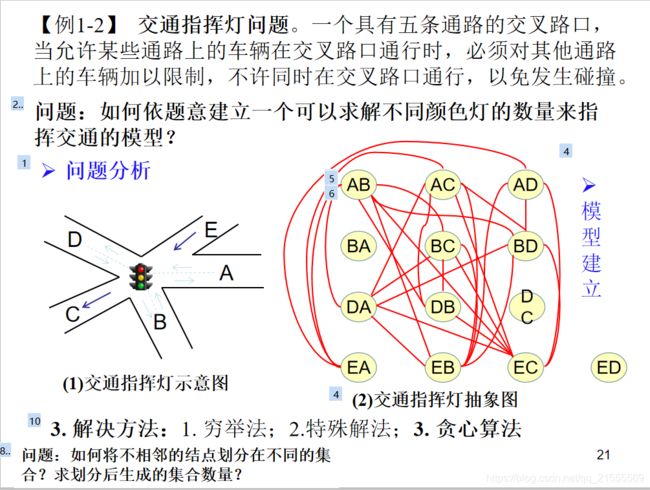
解决思路（穷举法）

这个问题是典型的图的涂色问题，即对图中每个顶点涂色，且相邻的顶点不能涂同一种颜色，求最少的颜色数

1. 首先求通路的个数
   可以用排列组合的方法，依次固定每个岔路为入口，例如固定A为入口，则有D、C、B 3种出口，同理B和D也是3种，E有4种，这样计算出来一共是4+3*3=13种。
2. 准备一个颜色数组int v[13] = {0}存放每个通路对应的颜色。
3. 准备一个矩阵bool e[13][13]，存储节点的边信息，其中节点代表通路，如AB，如果两个通路冲突，则在这两个节点之间连一条边，相应的在矩阵中对应位置就为1。
4. 写一个递归函数，递归地尝试每一个顶点对应的颜色是否满足要求。例如：假如共有两种颜色，每个通路的颜色从0开始测试，第一个通路颜色肯定为0，下一个顶点也从0开始尝试，共有两种情况（0，1），每选一种颜色都要与他前面的所有通路相比较（在这里是第一个通路），如果它与前面的某个通路颜色相同且相邻，则颜色序号加1，当颜色序号等于颜色总数时，循环结束，如果所有的顶点都被上色，即尝试完所有的通路，说明找到了当前颜色数目对应的方案，输出结果，退出程序。
5. 从颜色数目为2（不可能只有一个信号灯）开始循环，调用递归函数，每次调用颜色数目加一。

实现代码

// 交通灯穷举版本.cpp : 此文件包含 "main" 函数。程序执行将在此处开始并结束。
//

#include 

using namespace std;

int v[13] = { 0 };
bool e[13][13] = {
				{0,0,0,0,0,0,0,0,0,0,0,0,0},
				{0,0,0,0,0,1,1,1,0,0,1,1,0},
				{0,0,0,0,0,1,0,0,0,1,1,1,0},
				{0,0,0,0,0,0,0,0,0,0,0,0,0},
				{0,0,0,0,0,0,1,1,0,0,1,1,1},
				{0,1,1,0,0,0,1,0,0,0,1,1,1},
				{0,1,0,0,1,1,0,0,0,0,1,1,1},
				{0,1,0,0,1,0,0,0,0,0,0,1,1},
				{0,0,0,0,0,0,0,0,0,0,0,0,0},
				{0,0,1,0,0,0,0,0,0,0,0,0,1},
				{0,1,1,0,1,1,1,0,0,0,0,0,1},
				{0,1,1,0,1,1,1,1,0,0,0,0,1},
				{0,0,0,0,1,1,1,1,0,1,1,1,0}
};
//涂色函数
void dye(int cur_v, int color_num)
{
	//出口
	if (cur_v == 13)
	{
		cout << "最后的亮灯方案：";
		for (int i = 0; i < 13; i++)
		{
			cout << v[i] << " ";
		}
		cout << endl;
		cout << "共" << color_num << "种颜色" << endl;
		exit(0);
	}
	//cout << "color_num = " << color_num << ", cur_v = " << cur_v << endl;
	//依次测试每一种颜色
	for (int i = 0; i < color_num; i++)
	{
		v[cur_v] = i;
		bool ok = true;
		//对cur_v之前的节点进行冲突探测
		for (int j = 0; j < cur_v; j++)
		{
			if (v[cur_v] == v[j] && e[cur_v][j] == 1)
			{
				ok = false;
				break;
			}
		}
		if (ok)
		{
			//递归涂下一个顶点
			dye(cur_v + 1, color_num);
		}
	}
}

int main()
{
	for (int color_num = 2; color_num <= 13; color_num++)
	{
		dye(0, color_num);
	}
}

运算结果：0, 0, 0, 0, 1, 1, 2, 2, 0, 1, 3, 3, 0

贪心算法

贪心算法并不能保证最优解，直接贴上代码

#include 

using namespace std;

struct Node
{
	char name[8];
	int color;
};
void main()
{
	int cnt_color = 1;
	int i, j;
	Node v[13] = {
		{"ED",0}, {"AC",0}, {"AD",0}, {"BA",0}, {"BC",0},
		{"BD",0}, {"DA",0}, {"DB",0}, {"DC",0}, {"EA",0},
		{ "EB",0},{"EC",0},{ "AB", 0}
	};
	bool e[13][13] = {
						{0,0,0,0,0,0,0,0,0,0,0,0,0},
						{0,0,0,0,0,1,1,1,0,0,1,1,0},
						{0,0,0,0,0,1,0,0,0,1,1,1,0},
						{0,0,0,0,0,0,0,0,0,0,0,0,0},
						{0,0,0,0,0,0,1,1,0,0,1,1,1},
						{0,1,1,0,0,0,1,0,0,0,1,1,1},
						{0,1,0,0,1,1,0,0,0,0,1,1,1},
						{0,1,0,0,1,0,0,0,0,0,0,1,1},
						{0,0,0,0,0,0,0,0,0,0,0,0,0},
						{0,0,1,0,0,0,0,0,0,0,0,0,1},
						{0,1,1,0,1,1,1,0,0,0,0,0,1},
						{0,1,1,0,1,1,1,1,0,0,0,0,1},
						{0,0,0,0,1,1,1,1,0,1,1,1,0}
					};
	int result[13] = { 0 };
	for (i = 0; i < 13; i++)
	{
		if (v[i].color == 0)//未被涂色
		{
			bool flag = true;
			v[i].color = cnt_color;
			printf("第%d种颜色节点:%5s", cnt_color,v[i].name);
			for (j = 1; j < 13; j++)
				if (e[i][j] == 0 && v[j].color == 0)
				{
					for (int k = 0; k < 13; k++)
					{
						if (v[k].color == v[i].color &&
						e[j][k] == 1)//j与和i相同颜色的点相邻
						{
							flag = false;
						}
					}
					if (flag)
					{
						v[j].color = cnt_color;
						printf("%5s", v[j].name);
					}
				}
				cnt_color++;
				printf("\n");
		}
	}		
	printf("颜色总数: %d\n", cnt_color - 1);
	for (auto x : v)
	{
		printf("%s\t", x.name);
	}
	printf("\n");
	for (auto x : v)
	{
		printf("%d\t", x.color);
	}
}