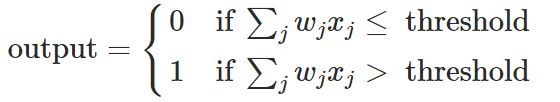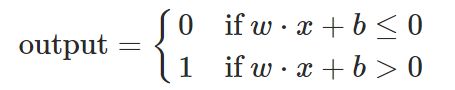神经网络第一章1.1感知机
感知机 (感知器)
什么是神经网络?为了方便开始讲述,我将解释一种叫做感知器的人工神经元。感知器是由科学家弗兰克·罗森布拉特在上世纪50年代和60年代开发的,灵感来自沃伦·麦卡洛赫和沃尔特·皮特的早期工作。如今,使用其他人工神经元模型的情况更为普遍——在许多现代的神经网络研究中,所使用的主要神经元模型是一种叫sigmoid 神经元。我们很快就会到达sigmoid 神经元。但是要理解为什么sigmoid 神经元是以其方式定义的,首先要花时间去理解感知器。
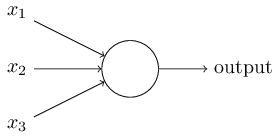
那么感知器是如何工作的呢?感知器接收几个二进制输入x1,x2,…,并产生一个二进制输出:
在上图示例中,感知器有三个输入,x1、x2、x3。一般来说,它可能有更多或更少的输入。罗森布拉特提出了一个简单的规则来计算输出。他介绍了权重,w1,w2,…,实数,表示输入对输出的重要性。神经元的输出0或1,取决于加权和∑j wj xj小于或大于某个阈值。就像权值一样,阈值是一个实数,它是神经元的参数。要用更精确的代数术语来表示:
这就是感知器的工作原理!
这就是基本的数学模型。你可以用一种方式来思考感知机,它是一种通过权衡证据来做出决定的设备。让我举个例子。这不是一个很现实的例子,但很容易理解,我们很快就会得到更现实的例子。假设周末快到了,你听说你的城市要举办美食节。你喜欢美食,正在考虑是否去参加这个节日。你可以通过权衡三个因素来做出决定:
1. 天气好吗?
2. 你的男朋友或女朋友想陪你吗?
3.临近公共交通吗(假设你没有车)。
我们可以用相应的二进制变量x1、x2和x3来表示这三个因素。例如,如果天气好,x1=1,如果天气不好,x1=0。同样,如果你的男朋友或女朋友想去,x2=1,如果不想去,x2=0。x3和公共交通也是如此。
现在,假设你非常喜欢美食,以至于你很高兴去参加这个节日,即使你的男朋友或女朋友不感兴趣,而且这个节日很难去。但也许你真的很讨厌坏天气,如果天气不好,你不可能去参加节日。你可以用感知器来模拟这种决策。一种方法是根据天气选择权重w1=6,其他条件选择权重w2=2和w3=2。w1的较大值表示天气对你来说非常重要,远比你的男朋友或女朋友是否加入你,或者离公共交通的距离更近。最后,假设您为感知器选择阈值5。通过这些选择,感知器实现所需的决策模型,每当天气好时输出1,每当天气不好时输出0。无论你的男朋友或女朋友是否想去,或者公共交通是否在附近,输出都没有区别。
通过改变权重和阈值,可以得到不同的决策模型。例如,假设我们选择了一个3的阈值,然后感知机会决定你应该在天气好的时候去参加这个节日,或者当两个节日都靠近公共交通并且你的男朋友或女朋友愿意加入你的时候。换句话说,这将是一种不同的决策模式。降低门槛意味着你更愿意去看电影节。
显然,感知器不是人类决策的完整模型!但这个例子说明的是,感知机如何权衡不同种类的证据,以便做出决定。一个复杂的感知机网络可以做出相当微妙的决定,这似乎是合理的: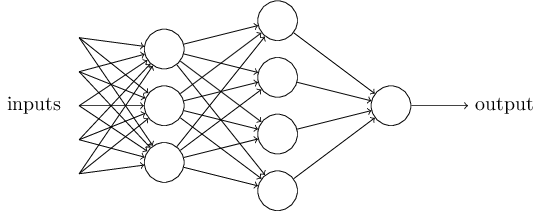
在这个网络中,感知器的第一列——我们称之为第一层感知器——通过权衡输入证据,做出了三个非常简单的决定。第二层的感知器呢?每个感知者都在通过权衡第一层决策的结果来做出决定。这样,第二层的感知器可以在比第一层的感知器更复杂更抽象的层次上作出决策。而更复杂的决策可以由感知者在第三层。这样,多层次的感知器网络就可以进行复杂的决策。
顺便说一下,当我定义感知器时,我说一个感知器只有一个输出。在感知器上方的网络中,它们看起来有多个输出。事实上,它们仍然是单一的输出。多个输出箭头只是一种有用的方法,它指示从感知器输出被用作对其他几个感知器的输入。这比绘制一条输出线然后分割的简单多了。
让我们简化描述感知器的方法。条件∑j wjxj>阈值很麻烦,我们可以做两个符号更改来简化它。第一个改变是写∑jwjxj作为点产品,w⋅十≡∑j wjxj,其中w和x分别是分量为权重和输入的向量。第二个改变是将阈值移到不等式的另一边,并用所谓的感知器偏差b来代替它阈值。使用偏差而不是阈值,可以重写感知器规则:
你可以把偏差看作是让感知器输出1的容易程度,或者用更生物学的术语来说,偏差就是让感知器发射的容易程度。对于一个有很大偏差的感知器来说,感知器输出1是非常容易的。但是如果偏差是非常负的,那么感知器就很难输出1。显然,引入偏差只是我们描述感知器的方式上的一个小变化,但是我们稍后会看到它会导致进一步的符号化简化。因此,在本书的其余部分中,我们将不使用阈值,而是始终使用偏差。
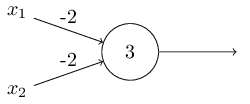
我把感知机描述成一种衡量证据以做出决定的方法。另一种使用感知器的方法是计算我们通常认为是基础计算的基本逻辑函数,如AND、OR和NAND。例如,假设我们有一个具有两个输入的感知器,每个输入都有权−2,总偏差为3。这是我们的感知机:
然后我们看到输入0 0产生输出1,因为(−2)∗0+(−2)∗0+3=3为正。在这里,我介绍了∗ 使乘法显式化的符号。类似的计算表明,输入0 1和1 0产生输出1。但是输入1 1产生输出0,因为(−2)∗1+(−2)∗1+3=−1为阴性。所以我们的感知器实现了与非门!
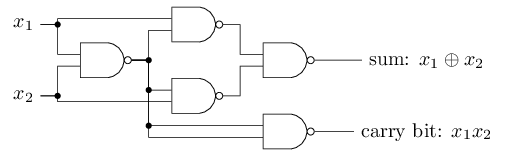
NAND的例子表明我们可以使用感知器来计算简单的逻辑函数。事实上,我们可以使用感知器网络来计算任何逻辑函数。原因是与非门是通用的计算,也就是说,我们可以建立任何计算出与非门。例如,我们可以使用与非门来构建一个加上两位x1和x2的电路。这需要计算位和x1⊕x2,以及当x1和x2都为1时设置为1的进位,即进位只是位积x1 x2:
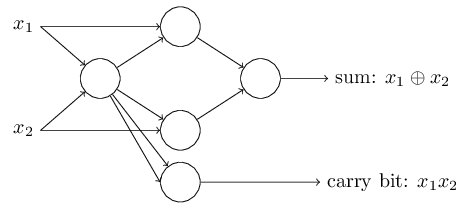
为了得到一个等效的感知器网络,我们用感知器替换所有的与非门,每个感知器有两个输入,每个输入都有权−2,总体偏差为3。这是结果网络。请注意,我移动了与右下角与非门相对应的感知器一点,以便更容易在图中绘制箭头:
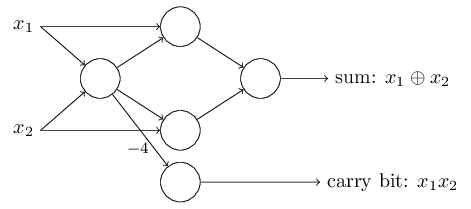
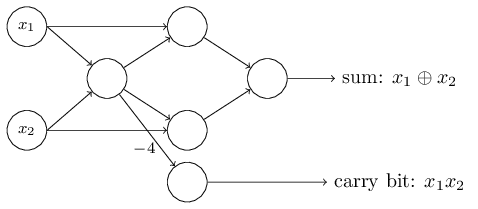
这个感知器网络的一个值得注意的方面是,最左边的感知器的输出被用作最下面的感知器的两倍输入。当我定义感知器模型时,我没有说是否允许这种双重输出到同一个地方。其实,没什么大不了的。如果我们不想允许这种情况,那么可以简单地将这两条线合并成一个权重为-4的连接,而不是两个权重为-2的连接(如果你没有发现这一点,你应该停下来向自己证明这是等价的。)通过这种改变,网络看起来如下,所有未标记的权重等于-2,所有偏差等于3,单个权重为-4,如标记所示:
到目前为止,我一直在画输入像x1和x2作为变量浮动到感知器网络的左侧。事实上,传统的做法是绘制一个额外的感知器层——输入层——来对输入进行编码:
输入感知器的符号,我们有输出,但没有输入,
这是速记标记。它实际上并不意味着没有输入的感知器。要看到这一点,假设我们有一个没有输入的感知器。然后是加权和∑j wj xj始终为零,因此如果b>0,感知器将输出1,如果b>0,感知器将输出0≤也就是说,感知器只会输出一个固定的值,而不是期望的值(x1,在上面的例子中)。最好不要把输入感知器看作真正的感知器,而是定义为输出期望值x1,x2,…,的特殊单元,…。
加法器示例演示了如何使用感知器网络来模拟包含多个与非门的电路。因为与非门是通用的计算,所以感知器也是通用的计算。
感知器的计算普遍性既令人放心又令人失望。这让人放心,因为它告诉我们,感知机网络可以像任何其他计算设备一样强大。但这也令人失望,因为它让人觉得感知器只是一种新型的与非门。这可不是什么大新闻!
然而,情况比这一观点所暗示的要好。结果表明,我们可以设计出学习算法,自动调整人工神经元网络的权值和偏差。这种调整是对外部刺激的响应,没有程序员的直接干预。这些学习算法使我们能够以一种与传统逻辑门截然不同的方式使用人工神经元。我们的神经网络可以简单地学习解决问题,而不是显式地设计一个由与非门和其他门组成的电路,有时直接设计传统电路会非常困难。