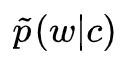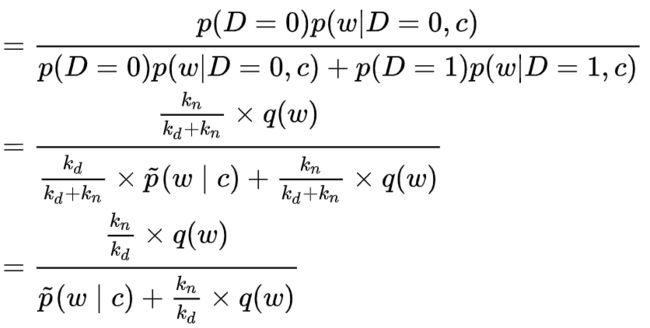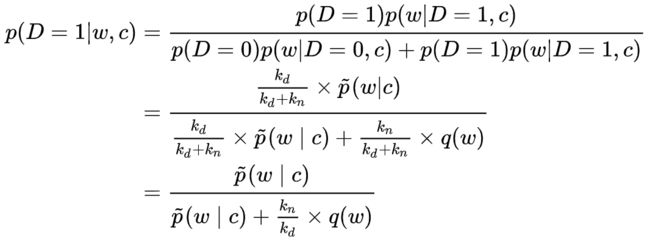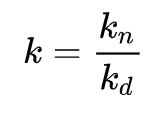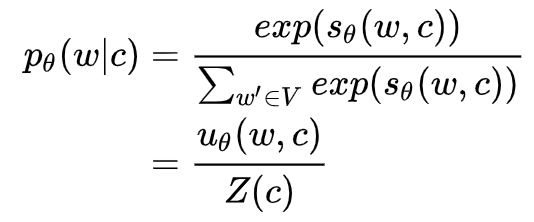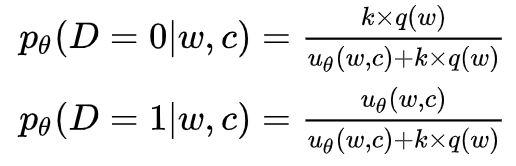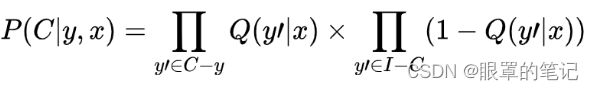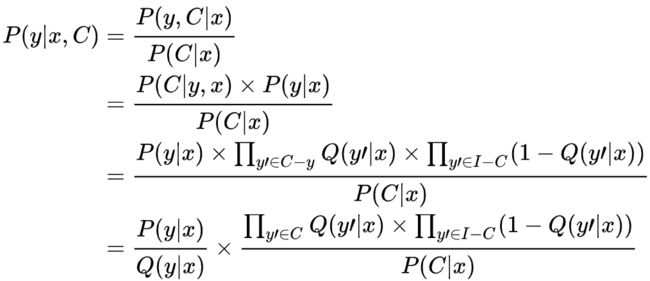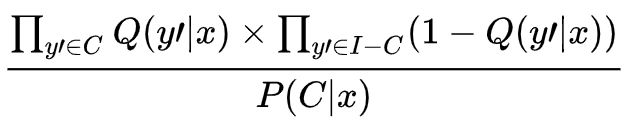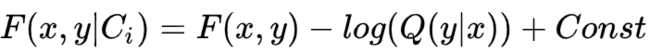一文讲懂召回中的 NCE & NEG & sampled softmax loss
深度学习中与分类相关的问题都会涉及到softmax的计算。当目标类别较少时,直接用标准的softmax公式进行计算没问题,当目标类别特别多时,则需采用估算近似的方法简化softmax中归一化的计算。
有很多讲解近似softmax 的文章,但都有一些细节上或者公式上的问题。今天这篇文章集百家所长,讲讲近似softmax的前世今生。
01 前提知识
1. logistic regression
逻辑回归的模型(函数/假设)为:
其中g为sigmoid函数,x为模型输入,θ为模型参数,hθ(x) 为模型预测正样本(类别为1)的概率。其对应的损失函数如下:
上述损失函数称为交叉熵损失,也叫log损失。通过优化算法(SGD/Adam)极小化该损失函数,可确定模型参数。
2. softmax loss
softmax回归的模型(函数/假设)为:
hθ表示第ii个样本输入x(i)x(i)属于各个类别的概率,且所有概率和为1。其对应的损失函数如下:
常将softmax + cross entropy loss称为softmax loss,softmax只是一个激活函数, 交叉熵才是损失函数, softmax loss其实是使用了softmax的交叉熵损失函数。
由上述softmax的假设函数可知,在学习阶段,每进行一个样本的类别估计都需要计算其属于各个类别的得分并归一化为概率值。当类别数特别大时,如语言模型中从海量词表中预测下一个词(词表中词即这里的类别),用标准的softmax进行预测就会出现分母计算量过大。
Approximate Softmax所解决的就是Softmax中分母的计算量太大的问题。怎么近似,又有如下的NCE和Sampled Softmax两种方法。
02 NCE
简单的讲,NCE的思想是将extreme large softmax转化为若干个二分类问题。
NCE 的核心思想就是通过学习数据分布样本和噪声分布样本之间的区别,从而发现数据中的一些特性,因为这个方法需要依靠与噪声数据进行对比,所以称为“噪声对比估计(Noise Contrastive Estimation)”。更具体来说,NCE 将问题转换成了一个二分类问题,分类器能够对数据样本和噪声样本进行二分类,通过最大化同一个目标函数来估计模型参数 。
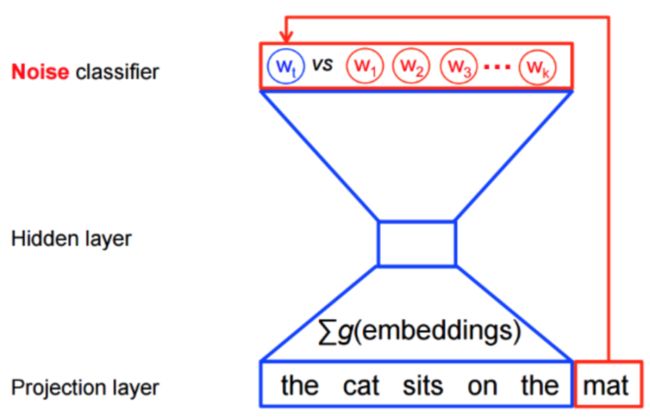
以语言模型为例,利用NCE可将从词表中预测某个词的多分类问题,转为从噪音词中区分出目标词的二分类问题。具体如图所示:
下面从数学角度看看具体如何构造转化后的目标函数(损失函数)。
记词wi的上下文为ci,
为从某种噪音分布Q中生成的K个噪音词(从词表中采样生成)。则(ci,wi)构成了正样本,
构成了负样本。
类比推荐领域,c 就是user, w 是target item , y 是label。
由于NCE会将一句话拆成若干二分类,所以共有k+1个样本。可看成从两种不同的分布中分别采样得到的,一个是依据训练集的经验分布
,与特定上下文c 有关;而另一个是与c无关的噪声分布为q(w),每次从词表中采样k个噪音样本。
假设现在取出了Kd 个正样本和Kn个负样本,这些正负样本混合形成一个混合分布 p(w|c)。
能得到下面这些概率:
所以可以计算后验概率:
我们再来定义一些符号:
2. 假设输入到 softmax 前的结果用
表示,实际上 是有含义的,它是一个 score function。于是有:
式中,
表示下一个单词是w 的概率;令表示当前单词库中所有单词的概率的累和,通常将这一项叫做“配分函数”或“归一化因子”。
NCE 所做的事情就是将式中的经验分布
替换成概率模型 ,使后验概率成为参数为的函数。但问题是这样现在这样的形式还是需要计算 ,我们只是将原来问题进行了一定的转换从而引入了噪声分布。为了解决这个问题,NCE 做了两个设定:
1)一个就是前面提到的,将
作为一个参数来进行估计,相当于引进了一个新的参数。
2)第二个是,事实证明(Mnih and Teh, 2012),对于参数很多的神经网络来说,我们将
固定为 1 对每个c 仍是有效的。
第二个设定,即减少了参数的数量,又使模型的输出符合”归一化“的性质,于是可以得到:
进一步变形,会发现一个很有意思的事情:
我们注意到这个其实是一个逻辑回归中的sigmoid函数。
就是user embedding与item embedding的点积,所以NCE 就是对双塔模型的输出了进行修正,修正量为。NCE 的损失函数就交叉熵损失函数。
NCE具有很好的理论保证:随着噪音样本数k的增加,NCE的导数趋向于softmax的梯度。有研究证明25个噪音样本足以匹配常规softmax的性能,且有45倍的加速。
对于设置的噪声分布 q(w),我们实际上是希望它尽量接近数据分布
,否则这个二分类任务就过于简单了,也就无法很好的学到数据特性。而作者通过实验和推导证明,当负样本和正样本数量之比k 越大,那么我们的 NCE 对于噪声分布好坏的依赖程度也就越小。换句话说,建议我们在计算能力运行的条件下,尽可能的增大比值k。也许这也就是大家都默认将正样本数量设置为 1 的原因:正样本至少取要 1 个,所以最大化比值k ,也就是尽可能取更多负样本的同时,将正样本数量取最小值 1。
03. Negative Sampling(NEG)
负采样(NEG)可看成是NCE的近似估计,其并不保证趋向于softmax。因为NEG的目标是学习高质量的词表示,而不是语言模型中的低困惑度(perplexity)。
NCE就是将多分类转化为一系列的二分类问题,二分类binary cross-entropy loss中所使用的是修正后的匹配度。
而NEG决定进一步简化,就不再修正了,直接用双塔的点乘,代入binary cross entropy 公式计算 loss。
优点:为了修正,计算、存储Q(w)还是比较麻烦的,比如要针对全库的item进行离线统计。NEG决定不再修正了,以上麻烦也就省略了,实现起来更简单。
缺点:NCE是有着很强的理论保证的,如果负采样足够多,那么nce loss的梯度与原始超大规模softmax的梯度趋于一致。但是NEG由于忽略了修正,因此没有“趋近原始softmax”的理论保证。但是由于我们大多数时候不关心点乘的结果,只是关心是否学习到高质量的user embedding & item embedding,因此理论上的瑕疵可以忍受,NEG在召回中应用得还是非常广泛的。
04 sampled softmax
sampled softmax思想是在全类别集合上,采样类别子集,然后在子集上计算logits 进行softmax。因为候选类别子集是采样的,大大减少了计算量,训练速度得到了优化。但问题是候选类别子集上的softmax该如何计算? 采样后 logits 与全类别 logits 计算上有什么差异?
用U2I场景来描述问题,给定一个用户 xi, 他点击的物料是 ti,再给他按照Q(y|x)采样一批负样本Si。原始softmax问题是,在整个物料库中哪个item是xi点击的,现在问题演变成在xi 的候选集
中,正确挑选出ti 的概率是多少。
数学符号约定:
-
(x,ti) 表示一条训练样本, x为输入特征, ti 为目标类别标签
-
P(y|x) 给定输入x, 输出类别为y的条件概率
-
F(x,y) 给定输入x, 输出类别为y的 logits, 其实表示的就是我们的模型
-
Q(y|x) 给定输入x, 采样出类别y的概率
-
Si 采样出来的类别子集
4.1 logits与概率之间的关系
等号两边同时取log,可以得到
最后将K(x)移项则可以得到
。即logits可以写成这种形式。
4.2 计算采样后类别子集Ci 上的概率分布
假设我们聚焦于第i个样本,以下公式中都省略下标i 。那么根据条件概率公式展开,
再对分子根据bayes公式展开,
。公式中的就是模型建模的目标,就是归一化后的F(x,y)。
现在聚焦于
,它代表在用户x和某一个物料y已经给定的情况下,构成整个候选集C的概率,它就等于,C中每个物料被采样到的概率,与I-C(I代表整个物料库)中每个物料没被采样到的概率,它们的乘积,即
把以上公式结合起来,
其中第二项
是与当前预测的y无关的,因此可以写成一个只与xi 和 ci 有关的常数 ki,因此有
4.3 采样后类别子集Ci上的logits与原始logits关系
终于要到最后一步了,我们已经知道了采样后类别子集 Ci 和类别全集L上概率分布的关系,这时我们只需要利用1中的 logits与概率之间的关系,就可以得出采样后类别子集Ci上的logits和原始logits关系,推导如下,将
![]()
带入到2中最后推导出来的公式,得到:
其中与类别y无关的常数项都可以合并,则有:
大功告成!上面的公式就是我们进行采样后的logits与原始logits关系,具体的用法如下:
-
通过 Q(y|x) 对类别进行采样,得到一个类别子集 Ci
-
模型对采样类别子集 Ci中的类别分别计算logits(这样就不用在类别全集计算logits了),这里得到的其实是F(x,y)
-
对于计算出来的F(x,y),减去 log(Q(y|x)),就得到了我们采样后子集的 logits
-
使用F(x,y|Ci)作为softmax 输入,计算概率分布以及loss进行梯度下降
05 采样函数
从上面分析可以得到:
我们选取不同的采样函数 Q(y|x)
,那么结果也会不同,比如Tensorflow中有如下采样方式:
-
1. tf.nn.log_uniform_candidate_sampler
按照 log-uniform (Zipfian) 分布采样。
P(class) = (log(class + 2) - log(class + 1)) / log(range_max + 1)。在U2I场景下,class可以理解为item id,排名靠前的item被采样到的概率越大。所以,为了打压高热item,item id编号必须根据item的热度降序编号,越热门的item,排前越靠前,被负采样到的概率越高。
-
2. tf.nn.learned_unigram_candidate_sampler
按照训练数据中类别出现分布进行采样。
具体实现方式:1)初始化一个 [0, range_max] 的数组, 数组元素初始为1; 2) 在训练过程中碰到一个类别,就将相应数组元素加 1;3) 每次按照数组归一化得到的概率进行采样。
上述采样方式都和输入相关,而如果我们选择随机采样,那么选择每个类别的概率都相等,也就是说 Q(y|x) 对于每个类别来说都一样,可以看做一个常数,并到后面常数项中,所以有:
而logits 加上或者减去一个常数,对softmax 结果并没有影响,所以可以用原始logits代替采样后的logits。所以如果随机采样,构造子集后logits 不修正也是正确的。
06 结论
理论指导实践,代码中每一步都是有理论依据的,所以只有弄懂其背后的数学原理才能各个算法活学活用。
NCE 和 sampled softmax 公式推导上有很多相通的思想,因为模型F(x,y) 要代表全局上的概率分布,而模型使用的是采样后的数据,loss 也是求的采样后数据的loss,所以需要对于logits F(x,y)进行修正才能得到采样后的logtis F(x, y|c)。
而NCE的修正公式是:
sample softmax 的修正公式是:
修正之后 NCE 由于转化为了若干个二分类问题,所以使用sigmoid+ logloss, 而 sampled softmax 则使用 softmax+ logloss。
参考:
https://carlos9310.github.io/2019/10/15/Approximating-the-Softmax/
https://zhuanlan.zhihu.com/p/334772391
https://zhuanlan.zhihu.com/p/528862933
https://zhuanlan.zhihu.com/p/143830417
https://zhuanlan.zhihu.com/p/528862933