Games101 作业6 提高内容（SAH算法）

本文只应用于个人学习总结。

目录

一、模型分析

1、按空间平均分配（NAIVE）

2、按物体平均分配

二、SAH

1、原理分析

2、代码实现

---

在作业7​​​​​​中的BVHAccel模块中已经分析了BVH树的构建过程，其仅仅采用了简单粗暴的NAIVE方式（按最长轴空间等分）去对一个节点构建左右子树，这种方法在构建时是很快的，但在渲染的过程中就体现了其缺点。这里参考了这篇文章，对其进行了分析，并引出了这篇文章所提及的基于表面积的启发式评估划分方法（Surface Area Heuristic，SAH）。

一、模型分析

1、按空间平均分配（NAIVE）

 在NAIVE的建树情况下会出现如图这种情况，那么就会存在这样一种情况：如果光线与右边包围盒相交，在下一次迭代的过程中会计算3个物体的划分；而如果光线与左边包围盒相交，则只需要直接返回一个物体即可。

那么问题就出现了，我们会发现所构建的BVH树是不平衡的。在学习搜索树的过程中，我们了解到要使得搜索时间达到最优解，就需要构建的二叉搜索树是平衡二叉树。同样的，BVH树需要最快速的搜索到与光线相交的包围盒，如何使BVH树达到平衡就变成了解决问题的关键。

2、按物体平均分配

要使BVH树达到平衡，最简单的方法就是，将物体按数量进行等分。这样确实可以获得所期望的平衡树，但在执行过程中仍会出现一些问题。

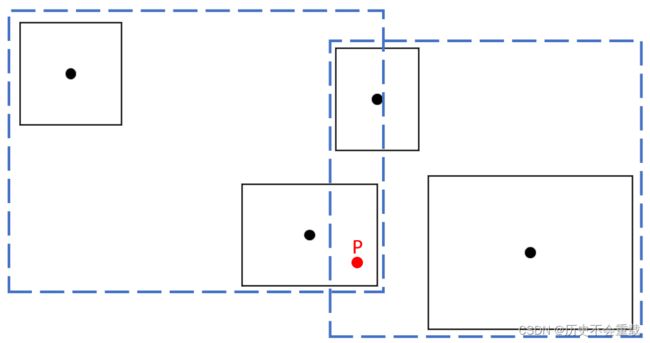
 如图所示，我们将物体按数量划分成了两个包围盒。但由于是空间划分，两个包围盒会产生重叠的部分，那么问题便产生了，如果一个光线相交于中间物体的P点，那么在查询物体交点的时候会经历了怎样的一个过程？P点在左右包围盒重叠的部分，所以两个包围盒都会与光线相交，整个过程在最坏情况下查询了所有的物体才能得到点P，这个查询过程花费的时间甚至大过了NAIVE所花费的时间，所以这种划分方式也不理想。

二、SAH

分析了以上两种简易划分方式，我们了解到，不论是按空间平均划分还是按数量平均划分，如果光线与两包围盒重叠位置相交，则都需要遍历两个包围盒才能得到交点。所以最优解就是将两包围盒的重叠区域控制在最小的划分方式，所以这里引出了一种常用且效果更好的基于表面积的启发式评估划分方法（Surface Area Heuristic，SAH）。

1、原理分析

SAH的目的是遍历所有可能的代价（Cost），得出使Cost最小的划分方式。

设整个包围盒C含有个物体，设对一个物体求交的代价为，那么就会有：

将这些物体分为AB两组，那么一条光线相交于AB的概率分别为和。由于AB两包围盒并非占满整个C包围盒并且可能产生重叠，所以。我们可以得到：

其中为遍历树状结构所需要的代价，通常设为0.125。我们假设每一个物体的求交代价都为1，A盒中物体个数为，B盒中物体个数为。光线相交子包围盒的概率，即为光线击中包围盒C的情况下击中子包围盒A/B表面的概率，若A盒表面积越大，则相交概率越大，B盒同理。由此我们可以总结为以下的公式：

2、代码实现

在作业6当中，修改BVH.cpp文件中构建BVH树的recursiveBuild函数即可。

BVHBuildNode* BVHAccel::recursiveBuild(std::vector objects)
{
    BVHBuildNode* node = new BVHBuildNode();

    // 建立当前节点总包围盒C
    Bounds3 bounds;
    for (int i = 0; i < objects.size(); ++i)
        bounds = Union(bounds, objects[i]->getBounds());
    if (objects.size() == 1) {
        // 如果包围盒内只有一个物体，此节点当作叶子节点
        node->bounds = objects[0]->getBounds();
        node->object = objects[0];
        node->left = nullptr;
        node->right = nullptr;
        return node;
    }
    else if (objects.size() == 2) {
        // 如果包围盒有两个物体，这两个物体分别作为左右叶子节点
        node->left = recursiveBuild(std::vector{objects[0]});
        node->right = recursiveBuild(std::vector{objects[1]});

        node->bounds = Union(node->left->bounds, node->right->bounds);
        return node;
    }
    else {
        // 如果有三个及以上物体，则选择最长轴方向将物体排序
        Bounds3 centroidBounds;
        for (int i = 0; i < objects.size(); ++i)
            centroidBounds =
                Union(centroidBounds, objects[i]->getBounds().Centroid());
        int dim = centroidBounds.maxExtent();
        switch (dim) {
        case 0:
            std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
                return f1->getBounds().Centroid().x <
                       f2->getBounds().Centroid().x;
            });
            break;
        case 1:
            std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
                return f1->getBounds().Centroid().y <
                       f2->getBounds().Centroid().y;
            });
            break;
        case 2:
            std::sort(objects.begin(), objects.end(), [](auto f1, auto f2) {
                return f1->getBounds().Centroid().z <
                       f2->getBounds().Centroid().z;
            });
            break;
        }

/**************************************   SAH   **************************************/
        int best_cut = 0;
        double min_cost = std::numeric_limits::max();

        // 遍历所有可能
        for(int index = 1; index < objects.size(); index++){
            // 分配物体
            auto leftshapes = std::vector(objects.begin(), objects.begin() + index);
            auto rightshapes = std::vector(objects.begin() + index, objects.end());
            assert(objects.size() == (leftshapes.size() + rightshapes.size()));

            // 建立左右包围盒
            Bounds3 bound_left, bound_right;
            for (int i = 0; i < leftshapes.size(); ++i)
                bound_left = Union(bound_left, leftshapes[i]->getBounds().Centroid());
            for (int i = 0; i < rightshapes.size(); ++i)
                bound_right = Union(bound_right, rightshapes[i]->getBounds().Centroid());

            // 获得表面积和数量
            auto S_left = bound_left.SurfaceArea();
            auto a = leftshapes.size();
            auto S_right = bound_right.SurfaceArea();
            auto b = rightshapes.size();
            auto S = bounds.SurfaceArea();

            // 计算cost
            auto cost = S_left / S * a + S_right / S * b;

            if(cost < min_cost){
                min_cost = cost;
                best_cut = index;
            }
        }

        auto beginning = objects.begin();
        auto middling = objects.begin() + best_cut;
        auto ending = objects.end();

        auto leftshapes = std::vector(beginning, middling);
        auto rightshapes = std::vector(middling, ending);

        assert(objects.size() == (leftshapes.size() + rightshapes.size()));

        node->left = recursiveBuild(leftshapes);
        node->right = recursiveBuild(rightshapes);

        node->bounds = Union(node->left->bounds, node->right->bounds);
    }

    return node;
}