【从RL到DRL】深度强化学习基础（三）——蒙特卡洛算法、TD算法改进：经验回放与高估问题的优化——Target网络与Double DQN，DQN结构改进——Dueling网络
目录
- 蒙特卡洛算法（Monte Carlo Algorithms）
-
- 例子：近似计算π
- 例子二：蒙特卡洛方法在定积分中的应用：
- 应用：蒙特卡洛近似期望（Expectation）
- Experience Replay 经验回放
-
- DQN与TD算法回顾
- 经验回放
- 改进：Prioritized Experience Replay 优先经验回放
- 高估问题
-
- Bootstrapping
- 高估问题（Problem of Overextimation）
- 解决方法一：Target Network
- 解决方法二：Double DQN
- Dueling Network
-
- 优势函数
- Dueling Network结构搭建：
蒙特卡洛算法（Monte Carlo Algorithms）
例子：近似计算π
如果有两个随机数生成器，可以生成[0,1]之间的数字，组成点的坐标(x,y)，则所有点构成的区域如下图：
而如果在这个区域中随机取点，点落在下图所示的圆形区域中的概率就可以表示为：
即P = A1/A2 = π r2/4 = π/4.
则如果选取了n个点，则落在圆形区域内的期望为：Pn = πn / 4 ,如果样本数量趋近于无穷，根据大数原则，可以使用频率来近似等于概率，就可以计算出π值。
例子二：蒙特卡洛方法在定积分中的应用：
如果给定一个函数f(x)，计算积分： 
从区间[a,b]中随机采样n个数据点，记为x1~xn，计算：
则Qn就可以用来近似积分值I，且当n→∞时，有Qn→I
应用：蒙特卡洛近似期望（Expectation）
记X为一随机向量，记p(x)为对应的概率密度函数（PDF），记f(x)为任意的函数，输入变量为一向量。则定义函数f(X)的期望：
直接求算这个期望往往不容易，尤其是当x为高维向量时，因此常采用蒙特卡洛算法来近似。过程如下：
- 基于概率密度函数随机抽取n个样本记为x1~xn。
- 计算函数f(x)在抽取的样本上的平均值：
- 将Qn作为函数f(X)的期望的预测值
Experience Replay 经验回放
DQN与TD算法回顾
DQN：通过神经网络训练动作价值函数Q(s,a;w)来近似最优动作价值函数Q*(s,a)
通常使用TD算法来训练DQN：
- 观测状态st并执行动作at
- 环境会提供一个新的状态st+1以及奖励rt
- TD target :
- TD error:
- 目标： 因为yt中考虑到了部分环境真实返回的回报rt，因此认为yt要比qt更加准确一点，因此训练目标就是使得qt逐渐接近接近yt。
TD 算法的缺点
将一次学习过程用到的四个数据(st,at,rt,st+1)定义为一个transition，并将所有的transitions记为经验(Experience)，
- 传统 的TD算法在使用了一次transition后便将其丢弃，实际上是一种经验浪费
- 此外，像上文中提到的状态st与st+1之间其实有很强的相关性，这种相关性往往不利于算法的学习。
经验回放
对于一个transition:(st,at,rt,st+1),将其存入一个容量为n个的空间中，称为replay buffer。这里的n是一个超参数，往往需要手动调试。但是一般情况下n会设置的比较大。
应用流程：
- 对于TD算法的目标函数：
- 从Buffer中随机抽取几个transition，求其LOSS函数值
- 对抽取的几个transition，分别求其LOSS函数的梯度，并对这些梯度求平均值
- 最后进行梯度下降（目的是使Loss函数最小）：
经验回放打破了过程见的联系性，具有了一定随机能力，同时多次重复利用了之前的经验
改进：Prioritized Experience Replay 优先经验回放
用非均匀抽样代替均匀抽样
基本思想：使用TD error来描述transition的重要性，如果一个transition有很高的TD error | δt |，它将会被赋予更高的优先级。
高估问题
Bootstrapping
To lift oneself up by his hoostraps.
在强化学习中，Bootstrapping的意思是用一个估算价值去更新同类的估算。TD算法实际上就用到了这一思想。
而在做SGD的梯度下降时，详细的表达式为：
SGD中的yt即用到了当前的动作值函数对下一个状态的估计，相当于用一个估计来更新现在状态的w值。
高估问题（Problem of Overextimation）
- TD算法中的TD Target项使用了max函数，使得target大于真实的动作价值
- Bootstrapping的存在加剧了高估问题的影响，会使高估更严重
- 回想DQN的网络流程，在SGD过程中的Bootstrapping现象会使得Q函数的高估加剧，而加剧后的Q函数的估计值反过来又继续作用与SGD过程中的Bootstrapping现象，这最后将是一个正循环的过程。
- 高估本事不是问题，只要是均匀的高估，对输出的动作价值函数输出动作时没有决策上的影响，但高估问题往往是不均匀的。
解决方法一：Target Network
在原来的TD算法的Q(s,a;w)网络的基础上，使用了一个新的网络Target Network：Q(s,a;w-)，只用来计算TD Target。而第一个网络用来控制Agent和收集经验（transitions）（四元组）。w-一般有两种更新方式：直接赋值法与加权平均法：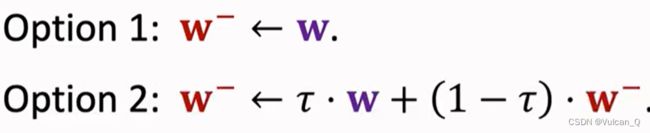
Target Network无法完全避免高估问题
解决方法二：Double DQN
- 第一步使用DQN进行动作决策
- yt则使用另一个TD Target网络来进行计算，则会有：
Double DQN也只是缓解了高估现象，也没有从根本上解决问题。
TD Network避免了Bootstrapping带来的高估问题，而Double DQN即避免了高估问题，又缓解了最大化带来的高估
Dueling Network
优势函数
前期回顾：
定义了优势函数A*(s,a)，即当前动作相对于Baseline的优势，动作a越好，它的优势就越大。
定理1：
所以可以很明显地看出，当优势函数A取得最大值时，动作动作价值函数Q也取得最大值，恰等于V*，则有：
那么既然有maxA*(s,a) = 0，就可以对A的定义式做变形，移项后就可以得到Q的表达式，也即定理2：
Dueling Network结构搭建：
先回顾一下DQN的结构：
再看预测Advantage Function的网络结构，通过神经网络函数A(s,a;wA) 来近似A*(s,a)。
并通过一个神经网络函数V(s;wV)来近似状态价值函数V(s)。只不过这个神经网络的输出参数为一个实数，用来给状态s打分。
因此，这里我们使用者两个神经网络近似后的函数V与A来替换定理2中的V与A，得到新的表达式：
实际情况下，使用 均值函数means会比max效果更好 。根据这个最终的公式，可以得到Dueling Network* 的网络结构示意图，网络的最终输出为在状态s下执行不同动作的价值评分Q，为一个向量。Dueling Network与DQN网络只有结构不同，输入、输出、功能等其他因素完全相同，训练方式也一致。
