LC刷题-GT

347.前K个高频元素——最小堆

HashMap+小顶堆：

class Solution {
    public int[] topKFrequent(int[] nums, int k) {
        / 最小堆（优先队列）+ HashMap
        Map<Integer,Integer> memo = new HashMap();
        for(int num : nums){
            memo.put(num,memo.containsKey(num) ? memo.get(num) + 1 : 1);
        }
        / PriorityQueue(Comparator c)优先队列构造器传入比较规则
        PriorityQueue<int[]> minQueen = new PriorityQueue(new Comparator<int[]>(){
            @Override//new Comparator对象中重写compare函数
            public int compare(int[] m,int[] n){
                return m[1] - n[1];//默认升序排列，也就是最小堆。
            } /这里的new Comparator是匿名内部类写法，可以进一步用Lambda简化代码(int[] m,int[] n)->{return m[1] - n[1];//默认升序排列，也就是最小堆。} 
        });

        for(Map.Entry<Integer,Integer> entry : memo.entrySet()){
            int key = entry.getKey(),value = entry.getValue();/ 遍历HashMap的键值对
            minQueen.offer(new int[]{key,value});
            if(minQueen.size() > k){
                minQueen.poll();
            }
        }

        int[] res = new int[k];
        for(int i = 0;i < k;i++){
            res[i] = minQueen.poll()[0];
        }
        return res;

    }
}

5.最大回文子串——动态规划（首尾的两个字母去除之后，它仍然是个回文串。）

动态规划：回文串，并且长度大于 22，那么将它首尾的两个字母去除之后，它仍然是个回文串。
dp数组含义为i - j之间的子串是否为回文子串；i <= j
状态转移过程中，利用reslen,begin,end来获取子串的长度并记录下最大长度子串的起始索引。

class Solution {
    public String longestPalindrome(String s) {
        int len = s.length();
        
        boolean[][] dp = new boolean[len][len];//dp数组含义为i - j之间的子串是否为回文子串；i <= j
        for(int i = 0;i < len;i++){
            dp[i][i] = true;
        }
        int reslen = 1;
        int begin = 0,end = 0;
        //草图绘制判断循环方向
        for(int i = len - 2;i >= 0;i--){
            for(int j = i + 1;j < len;j++){
                if(s.charAt(i) == s.charAt(j)){
                    if(i + 1 > j - 1){
                        dp[i][j] = true;
                    }else{
                        dp[i][j] = dp[i + 1][j - 1];
                    }

                    //判断回文子串的长度是否最大，最大则记录起始位置
                    if(dp[i][j] == true){
                        if(j - i + 1 > reslen){
                            begin = i;
                            end = j;
                            reslen = j - i + 1;
                        }
                    }
                }else{
                    dp[i][j] = false;
                }
            }
        }

        return end == len - 1 ? s.substring(begin) : s.substring(begin,end + 1);
    }
}

11.盛最多水的容器——左右双指针，移动高度较小的那个指针来缩减范围

俩层for循环，超时。
class Solution {
    public int maxArea(int[] height) {
        int res = 0;
        for(int i = 0;i < height.length;i++){
            for(int j = i;j < height.length;j++){
                res = Math.max(res,(j - i) * Math.min(height[i],height[j]));
            }
        }
    return res;
    }
}

双指针
初始时，左右指针分别指向数组的左右两端
容纳的水量是由:两个指针指向的数字中较小值 * 指针之间的距离
移动 数字较小的那个指针;

class Solution {
    public int maxArea(int[] height) {
        int res = 0;
        int left = 0,right = height.length - 1;
        while(left < right){
            res = Math.max(res,(right - left) * Math.min(height[left],height[right]));
            if(height[left] > height[right]){
                right--;
            }else{
                left++;
            }
        }

    return res;
    }
}

15.三数之和

各层优化，去除不必要的分支。
排序（用于解决重复问题）+三指针
三数之和还有最接近的三数之和这类题用回溯都会超时，
只能用三层for循环，同时一开始对原数组排序
后续在每一层循环里进行剪枝操作

class Solution {
    //遍历回溯；三层选择；
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList();
        List<Integer> list = new ArrayList();
        Arrays.sort(nums);//排序和(i > 0 && nums[i] == nums[i - 1]) continue;解决重复问题
        // Set memoset = new HashSet();//用于记录添加的list避免三元组重复

        int len = nums.length;
        int third = 0;
        for(int i = 0;i < len - 2;i++){
            if(nums[i] > 0){//因为已经排好序了，若第一个元素就大于零，那么后面的都大于零，也就没必要继续遍历了。以消除多余分支
                break;
            }
            if(i > 0 && nums[i] == nums[i - 1]){//第一个元素为该元素的已经遍历过了，后续出现相同的需要跳过
                continue;
            }
            for(int j = i + 1;j <len - 1;j++){
                if(nums[i] + nums[j] > 0){
                    break;
                }
                if(j > i + 1 && nums[j] == nums[j - 1]){
                    continue;
                }
                third = j + 1;
                while(third < len){
                    if(nums[i] + nums[j] + nums[third] > 0){
                        break;
                    }
                    if(nums[i] + nums[j] + nums[third] == 0){
                        list.add(nums[i]);
                        list.add(nums[j]);
                        list.add(nums[third]);
                        result.add(new ArrayList(list));
                        list.clear();
                        break;
                    }
                    third++;
                }
            }
        }
        return result;
    }
}

俩数之和：考虑用hashmap保存目标target-nums[i]；
回溯：——超时

class Solution {
    private int len;
    private List<List<Integer>> res;
    public List<List<Integer>> threeSum(int[] nums) {
        this.len = nums.length;
        res = new ArrayList();
        List<Integer> list = new ArrayList();
        Arrays.sort(nums);
        backtrack(nums,list,0,0);

        return res;
    }

    public void backtrack(int[] nums,List<Integer> list,int target,int start){
        if(list.size() == 3){
            res.add(new ArrayList<Integer>(list));
            return;
        }

        for(int i = start;i < len;i++){
            if((i > start && nums[i] == nums[i - 1])){//i>start用于保证该层不会选到重复的元素
                continue;
            }else if(list.size() == 2 && nums[i] != target){
                continue;
            }else if(nums[i] > target){
                break;
            }

            list.add(nums[i]);
            backtrack(nums,list,target - nums[i],i + 1);
            list.remove(list.size() - 1);

        }

        return;
    }
}

超时,三层for循环超出时间限制。时间复杂度O(n3)；利用HashMap也使得空间复杂度较高
class Solution {
    //遍历回溯；三层选择；
    public List<List<Integer>> threeSum(int[] nums) {
        List<List<Integer>> result = new ArrayList();
        List<Integer> list = new ArrayList();
        Arrays.sort(nums);
        Set<String> memoset = new HashSet();//用于记录添加的list避免三元组重复

        int sum = 0,len = nums.length;
        for(int i = 0;i < len - 2;i++){
            list.add(nums[i]);
            sum += nums[i];
            for(int j = i + 1;j <len - 1;j++){
                list.add(nums[j]);
                sum += nums[j];
                for(int k = j + 1;k < len;k++){
                    list.add(nums[k]);
                    sum += nums[k];
                    if(sum == 0){
                        String s = String.valueOf(list.get(0)) + String.valueOf(list.get(1)) + String.valueOf(list.get(2));
                        if(!memoset.contains(s)){
                            memoset.add(s);
                            result.add(new ArrayList(list));
                        }
                    }
                    //回溯第三层
                    sum -= nums[k];
                    list.remove(2);
                }
                //回溯第二层
                sum -= nums[j];
                list.remove(1);
            }
            //回溯第一层
            sum -= nums[i];
            list.remove(0);
        }
        return result;
    }

}

17.电话号码的字符组合（递归+回溯） √√√

这里有个关键点要注意：char转int不能用强转，（int）/Integer.valueOf()；这样转的话得到的是char字符的ASCII 码;可以用c - '0’来获取

class Solution {
    //全排列问题；递归(终止条件获取结果条件设置+做选择+添加下一层递归函数)+回溯
    public List<String> result = new ArrayList();
    public int len = 0;
    public String[] digitsstring = new String[]{"","","abc","def","ghi","jkl","mno","pqrs","tuv","wxyz"};//也可以用哈希表来获取索引与可选字符串的对应关系
    public List<String> letterCombinations(String digits) {
        len = digits.length();
        if(len == 0){
            return result;
        }
        StringBuilder sb = new StringBuilder();
        backtrack(digits,0,sb);

        return result;

    }
    public void backtrack(String digits,int count,StringBuilder sb){
        if(count == len){
            result.add(sb.toString());
            return;
        }

        String backstring = digitsstring[digits.charAt(count) - '0'];
        for(int i = 0;i < backstring.length();i++){
            sb.append(backstring.charAt(i));
            backtrack(digits,count + 1,sb);
            sb.deleteCharAt(count);//回溯
        }

    }
}

134.加油站
暴力穷举 遍历——超出时限

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int len = gas.length;
        
        // List list = new ArrayList();
        for(int i = 0;i < len;i++){//遍历起始点  
            int res = util(gas,cost,i);
            if(res != -1){
                return i;
            }
        }

        return -1;
    }

    public int util(int[] gas,int[] cost,int start){
        int gashaving = 0;
        int i = start;
        gashaving += gas[i];
        gashaving -= cost[i];
        if(gashaving < 0){
            return -1;
        }
        i++;
        if(i == gas.length){
            i = 0;
        }
        while(i != start){
            
            gashaving += gas[i];
            gashaving -= cost[i];
            if(gashaving < 0){
                return -1;
            }
            i++;
            if(i == gas.length){
                i = 0;
            }
        }
        return start;
    }
}

使用穷举法时，考虑题目意义，看能不能消减分支来减少时间复杂度；
我们首先检查第 0个加油站，并试图判断能否环绕一周；如果不能，就从第一个无法到达的第i个加油站开始继续检查。
这是因为从0开始可以到i中间的站,则到这些站时,所剩油量也是>=0的，故从0开始都到不了i，则中间站起始也必然到不了i站，只能从i开始

class Solution {
    public int canCompleteCircuit(int[] gas, int[] cost) {
        int len = gas.length;
        int start = 0;
        int gashaving = 0;

        while(start < len){
            int i = start;
            gashaving = 0;
            while(i < start + len){
                if(i < len){
                    gashaving += gas[i];
                    gashaving -= cost[i];
                }else{
                    gashaving += gas[i - len];
                    gashaving -= cost[i - len];
                }
                i++;//到达下一站

                if(gashaving < 0){//判断是否油够
                    break;
                }
            }

            if(i == start + len && gashaving >= 0){
                return start;//退出循环，要么遍历完成，要么出现gashaving<0
            }else{
                start = i;
            }
        }
        return -1;
    }
}

22.括号生成 （递归，回溯）√√√
根据左右括号剩余个数ln和rn分情况做选择与回溯
或者利用visited[]{ln,rn}来记录剩余括号数；然后在递归函数中进行左右括号数的分类讨论该层递归函数中可选取得情况；回溯；直至左右括号剩余为零。

class Solution {
    //全排列：递归+回溯
    public List<String> result = new ArrayList();

    public List<String> generateParenthesis(int n) {
        // List result = new ArrayList();
        StringBuilder sb = new StringBuilder();
        backtrack(n,n,sb);//n为起始左右括号个数

        return result;
    }
    public void backtrack(int ln,int rn,StringBuilder sb){
        //分情况做选择与回溯
        if(ln == 0 && rn == 0){
            result.add(sb.toString());
            return;
        }else if(ln == 0){
            sb.append(")");
            backtrack(ln,rn - 1,sb);
            sb.deleteCharAt(sb.length() - 1);//做完选择后要回溯
        }else if(rn > ln){
            sb.append("(");
            backtrack(ln - 1,rn,sb);
            sb.deleteCharAt(sb.length() - 1);
            sb.append(")");
            backtrack(ln,rn - 1,sb);
            sb.deleteCharAt(sb.length() - 1);
        }else{
            sb.append("(");
            backtrack(ln - 1,rn,sb);
            sb.deleteCharAt(sb.length() - 1);
        }
    }
}

23.合并K个升序链表 √√√
// //考虑实现俩个升序链表的合并，然后在k个中循环完成K个链表合并.如此时间复杂度比直接进行K个链表的第一个节点比大小要复杂
// public ListNode sortNode(ListNode ln1,ListNode ln2){}
故直接利用for循环找出K个头节点的最小节点

/**
 * Definition for singly-linked list.
 * public class ListNode {
 *     int val;
 *     ListNode next;
 *     ListNode() {}
 *     ListNode(int val) { this.val = val; }
 *     ListNode(int val, ListNode next) { this.val = val; this.next = next; }
 * }
 */
class Solution {
    public ListNode mergeKLists(ListNode[] lists) {
        ListNode start = new ListNode(Integer.MAX_VALUE);
        int index = -1;//用于保存最小节点的索引，以便最后删除最小节点
        for(int i = 0;i < lists.length;i++){//遍历获取k个升序链表的第一个节点的val最小值
            if(lists[i] == null){
                continue;//某个链表遍历完的情况跳过
            }
            if(lists[i].val < start.val){
                start.val = lists[i].val;
                index = i;
            }
        }
        if(index == -1){//判断是否K个链表都遍历完了
            return null;
        }else{
            lists[index] = lists[index].next;//删除第一个节点最小的链表第一个节点
            start.next = mergeKLists(lists);//当前节点的next应该为剩下K个链表第一个节点的最小节点
            return start;
        }
    }
}

31.下一个排列√√√

class Solution {
    //数组升序后进行回溯全排列，所得的结果就是字典顺序从小到大的结果；所以只需要找到nums在其升序后回溯排序中得到nums结果时回溯出一个结果即可
    //具体步骤可思考全排列上下俩个结果的回溯过程
    //这里是从后往前遍历数组，找到第一个nums[i + 1] > nums[i]处。那么从i处开始往后进行回溯，即找到只大nums[i]一级的元素放在i处，后续sort即可。若没有nums[i + 1] > nums[i]，说明这个nums是最后一个，那么只要返回第一个，即sort的nums即可
    //
    public void nextPermutation(int[] nums) {
        int len = nums.length;
        int i = len - 2;
        while(i >= 0){
            if(nums[i + 1] > nums[i]){
                break;
            }
            i--;
        }
        if(i == -1){
            Arrays.sort(nums);
        }else{
            //找到比nums[i]大一级的元素及索引
            int eachindex = i + 1;
            for(int j = i + 1;j < len;j++){
                if(nums[j] > nums[i] && nums[j] < nums[eachindex]){
                    eachindex = j;
                }
            }
            //交换后，对后续排序升序
            int temp = nums[i];
            nums[i] = nums[eachindex];
            nums[eachindex] = temp;
            Arrays.sort(nums,i + 1,nums.length);
        }
        return;
    }
}

32.最长有效括号（困难，困难，困难）

class Solution {
    public int longestValidParentheses(String s) {
        int maxans = 0;
        int[] dp = new int[s.length()];//以i处括号结尾的最长子串。数组默认值为零
        for (int i = 1; i < s.length(); i++) {
            if (s.charAt(i) == ')') {
                if (s.charAt(i - 1) == '(') {
                    dp[i] = (i >= 2 ? dp[i - 2] : 0) + 2;
                } else if (i - dp[i - 1] > 0 && s.charAt(i - dp[i - 1] - 1) == '(') {//得保证subs左边还有元素，所以i - dp[i - 1] > 0;否则dp[i] = 0默认值
                    dp[i] = dp[i - 1] + ((i - dp[i - 1]) >= 2 ? dp[i - dp[i - 1] - 2] : 0) + 2;//当前i处')'对应的'('左侧是否为有效子串dp[i - dp[i - 1] - 2] 
                }
                maxans = Math.max(maxans, dp[i]);
            }
        }
        return maxans;
    }
}

33.搜索旋转排序数组√√√

class Solution {
    // O(log n)考虑二分法。
    /先找到旋转位置;再判断target在前段还是后段，再用二分查找
    public int search(int[] nums, int target) {
        int len = nums.length;
        if(len == 1){
            return nums[0] == target ? 0 : -1;
        }
        int k = getindex(nums);//获取旋转索引

        int left = 0,right = len - 1;
        if(nums[0] <= target && target <= nums[k]){
            left = 0;
            right = k;
        }else if(nums[k + 1] <= target && target <= nums[len - 1]){
            left = k + 1;
        }else{
            return -1;
        }

        return searchtarget(nums,left,right,target);
    }
    public int getindex(int[] nums){
        int k = 0;
        while(k < nums.length - 1){
            if(nums[k] > nums[k + 1]){
                return k;
            }
            k++;
        }
        return 0;
    }

    public int searchtarget(int[] nums,int left,int right,int target){
        int mid = 0;
        while(left <= right){
            mid = (left + right) / 2;
            if(target < nums[mid]){
                right = mid - 1;
            }else if(target > nums[mid]){
                left = mid + 1;
            }else{
                return mid;
            }
        }
        return -1;
    }
}

或者：
可以在常规二分查找的时候查看当前 mid 为分割位置分割出来的两个部分 [l, mid] 和 [mid + 1, r] 哪个部分是有序的，并根据有序的那个部分确定我们该如何改变二分查找的上下界，因为我们能够根据有序的那部分判断出 target 在不在这个部分

class Solution {
    // O(log n)考虑二分法。
    //先找到旋转位置;再判断target在前段还是后段，再用二分查找
    public int search(int[] nums, int target) {
        int len = nums.length;
        if(len == 1){
            return nums[0] == target ? 0 : -1;
        }

        int left = 0,right = len - 1,mid = 0;
        while(left <= right){
            mid = (left + right) / 2;
            if(nums[mid] == target){
                return mid;
            }
            if(nums[left] <= nums[mid]){//左边为有序
                //判断target是否在这半边
                if(target >= nums[left] && target < nums[mid]){//与nums[mid]比较不需要等号是因为上面已经对比过了
                    right = mid - 1;
                }else{
                    left = mid + 1;
                }
            }else{//右边有序
                if(target > nums[mid] && target <= nums[right]){
                    left = mid + 1;
                }else{
                    right = mid - 1;
                }
            }
        }
        return -1;
    }

}

42.接雨水
1.动态规划

记录i处左右（包含i处）最高的高度；用于计算i处所能接下的雨水
class Solution {
    public int trap(int[] height) {
        int len = height.length;
        int[] leftMax = new int[len],rightMax = new int[len];//记录i处左右最高的高度；用于计算i处所能接下的雨水

        leftMax[0] = height[0];
        rightMax[len - 1] = height[len - 1];
        //动态规划获取俩数组在i处的左右最高高度
        for(int i = 1;i < len;i++){
            leftMax[i] = Math.max(leftMax[i - 1],height[i]);
        }
        for(int i = len - 2;i >= 0;i--){
            rightMax[i] = Math.max(rightMax[i + 1],height[i]);
        }

        int sum = 0;
        for(int i = 0;i < len;i++){
            sum += Math.min(leftMax[i],rightMax[i]) - height[i];
        }
        return sum;
    }
}

48.旋转图像 √√√
实现原地旋转：
int temp = matrix[start][start + j];
matrix[start][start + j] = matrix[start + sideadd - j][start];
matrix[start + sideadd - j][start] = matrix[start + sideadd][start + sideadd - j];
matrix[start + sideadd][start + sideadd - j] = matrix[start + j][start + sideadd];
matrix[start + j][start + sideadd] = temp;

不使用额外空间，原地旋转
class Solution {
    public void rotate(int[][] matrix) {
        int len = matrix.length;
        rotateutil(matrix,0,len);//传入矩阵，当前层旋转起点，当前层旋转边长

        return;
    }

    public void rotateutil(int[][] matrix,int start,int sidelen){
        if(sidelen < 2){
            return;
        }
        int sideadd = sidelen - 1;
        for(int j = 0;j < sidelen - 1;j++){
            int temp = matrix[start][start + j];
            matrix[start][start + j] = matrix[start + sideadd - j][start];
            matrix[start + sideadd - j][start] = matrix[start + sideadd][start + sideadd - j];
            matrix[start + sideadd][start + sideadd - j] = matrix[start + j][start + sideadd];
            matrix[start + j][start + sideadd] = temp;
        }

        rotateutil(matrix,start + 1,sidelen - 2);
    }
}

双for循环：
class Solution {
    public void rotate(int[][] matrix) {
        int len = matrix.length;
        int sideadd = len - 1;
        for(int i = 0; i < len / 2;i++){//当前旋转层
            sideadd = len - 2 * i - 1;
            for(int j = 0;j < len - 2 * i - 1;j++){//当前层进行旋转的四个节点各距离该旋转层正方形角点的距离j
                int temp = matrix[i][i + j];
                matrix[i][i + j] = matrix[i + sideadd - j][i];
                matrix[i + sideadd - j][i] = matrix[i + sideadd][i + sideadd - j];
                matrix[i + sideadd][i + sideadd - j] = matrix[i + j][i + sideadd];
                matrix[i + j][i + sideadd] = temp;
            }
        }
        return;
    }

49.字母异位词分组√√√

class Solution {
    public List<List<String>> groupAnagrams(String[] strs) {
        Map<String,Integer> memo = new HashMap();//memo用于记录异位字符和相同异位字符串存于result中的位置
        List<List<String>> result = new ArrayList();
        int memoindex = 0;

        for(int i = 0;i < strs.length;i++){
            String flag = flagstring(strs[i]);
            if(memo.containsKey(flag)){
                result.get(memo.get(flag)).add(strs[i]);
            }else{
                List<String> list = new ArrayList<String>();
                list.add(strs[i]);
                result.add(list);
                memo.put(flag,memoindex);
                memoindex++;
            }
        }

        return result;
    }

    public String flagstring(String s){//获取异位字符串的唯一标识；用长度为26的数组表示并转为字符串
        int[] nums = new int[26];
        for(int i = 0;i < 26;i ++){
            nums[i] = 0;
        }
        for(int i = 0;i < s.length();i++){
            nums[s.charAt(i) - 'a'] += 1;
        }
        return Arrays.toString(nums);
    }
}

55.跳跃游戏

class Solution {
    /动态规划
    public boolean canJump(int[] nums) {
        int len = nums.length;
        boolean[] dp = new boolean[len];
        dp[len - 1] = true;

        /dp数组循环顺序应该是从后往前
        for(int i = len - 2;i >= 0;i--){
            for(int jumpspace = 1;jumpspace <= nums[i];jumpspace++){
                if(dp[i]){//删减分支
                    continue;
                }else if(jumpspace + i > len - 1){//删减分支
                    continue;
                }else{
                    dp[i] = dp[i] || dp[i + jumpspace];/状态转移
                }
            }
        }

        return dp[0];
    }
}

贪心：
贪心算法：每次达到最极限

class Solution {
    //动态规划
    public boolean canJump(int[] nums) {
        int len = nums.length;
        int farMax = 0;//最远可到达的索引处
        for(int i = 0;i < len;i++){
            if(i > farMax){//最远都到达不了i处，必然为false
                return false;
            }else{
                farMax = Math.max(farMax,i + nums[i]);//更新最远到达索引
            }
            
            if(farMax >= len - 1){
                return true;//最远到达索引达到了最后一个索引。返回true
            }
        }

        return false;
    }
}

56.合并区间

先排序

 /合并区间，类似信封问题，俄罗斯套娃问题，先排序
class Solution {
    public int[][] merge(int[][] intervals) {
        int len = intervals.length;
        //合并区间，类似信封问题，俄罗斯套娃问题，先排序
        Arrays.sort(intervals,new Comparator<int[]>() {
            @Override
            public int compare(int[] o1,int[] o2){
                return o1[0] - o2[0];
            }
        });

        List<int[]> list = new ArrayList();
        list.add(new int[]{intervals[0][0],intervals[0][1]});
        for(int i = 1;i < len;i++){
            if(intervals[i][0] > list.get(list.size() - 1)[1]){
                list.add(new int[]{intervals[i][0],intervals[i][1]});
            }else{
                list.get(list.size() - 1)[1] = Math.max(list.get(list.size() - 1)[1],intervals[i][1]);
            }
        }
        return list.toArray(new int[list.size()][]);

    }
}

75.颜色分类
1.单指针，俩次遍历；先将0全部置于前面，第二次遍历再从0后开始将1全部置于前面；

class Solution {
    public void sortColors(int[] nums) {
        int len = nums.length;
        if(len == 1){
            return;
        }
        //原地排序，不使用库;考虑指针
        int left = 0;
        for(int i = 0;i < len;i++){
            if(nums[i] == 0){
                while(left < len && nums[left] == 0){
                    left++;
                }
                if(i > left){
                    each(nums,i,left);
                }
            }
        }
        if(left >= len){//全部为0的情况
            return;
        }
        left = (nums[left] == 0 ? left + 1 : left);//没有0的情况
        for(int i = left;i < len;i++){
            if(nums[i] == 1){
                while(left < len && nums[left] == 1){
                    left++;
                }
                if(i > left){
                    each(nums,i,left);
                }
            }
        }

    }

    public void each(int[] nums,int i,int j){
        int temp = nums[i];
        nums[i] = nums[j];
        nums[j] = temp;
        return;
    }
}

单指针优化；不需要去找非0和非来替换，直接按索引顺序替换即可
class Solution {
    public void sortColors(int[] nums) {
        int len = nums.length;
        int ptr = 0;
        if(len == 1){
            return;
        }
        for(int i = 0;i < len;i++){
            if(nums[i] == 0){
                int temp = nums[i];
                nums[i] = nums[ptr];
                nums[ptr] = 0;
                ptr++;
            }
        }
        for(int i = ptr;i < len;i++){
            if(nums[i] == 1){
                int temp = nums[i];
                nums[i] = nums[ptr];
                nums[ptr] = 1;
                ptr++;
            }
        }
    }
}

双指针
一次遍历，将0交换到前面，将2交换到后面，

class Solution {
    public void sortColors(int[] nums) {
        int len = nums.length;
        int p0 = 0,p2 = len - 1;
        if(len == 1){
            return;
        }
        for(int i = 0;i < len;i++){
            
            if(nums[i] == 0){
                int temp = nums[i];
                nums[i] = nums[p0];
                nums[p0] = 0;
                p0++;
            }else if(nums[i] == 2 && i < p2){
                int temp = nums[i];
                nums[i] = nums[p2];
                nums[p2] = temp;
                p2--;
                i--;/i--是为了防止从后面交换到i处为0被i++跳过
            }
        }
        
    }
}

79.单词搜索
回溯

class Solution {
    // 回溯，visited用于标记已经用过的点
    private int row,col,len;
    private int[][] direction = {{0, 1}, {0, -1}, {1, 0}, {-1, 0}};

    public boolean exist(char[][] board, String word) {
        this.row = board.length;
        this.col = board[0].length;
        this.len = word.length();

        boolean[][] visited = new boolean[row][col];//visited用于标记已匹配过的路径

        for(int i = 0;i < row;i++){
            for(int j = 0;j < col;j++){//遍历
                boolean flag = isexist(board,word,i,j,0,visited);
                if(flag){
                    return true;
                }
            }
        }

        return false;
    }

    public boolean isexist(char[][] board, String word, int i, int j, int k , boolean[][] visited){

        if(board[i][j] == word.charAt(k)){
            if(k == len - 1){
                return true;//当前ij处与k处匹配，且k达到word的最后一个字符，则匹配完成
            }

            visited[i][j] = true; //添加进路径
            for(int di = 0;di < 4;di++){//当前节点做选择，考虑剪枝
                int newi = i + direction[di][0],newj = j + direction[di][1];
                if(newi >= row || newi < 0 || newj >= col || newj < 0){//索引超出边界，剪枝
                    continue;
                }else if(visited[newi][newj]){//索引回到已选路径，剪枝
                    continue;
                }
                boolean flag = isexist(board,word,newi,newj,k + 1,visited);
                if(flag){
                    return true;
                }
            }
            visited[i][j] = false;//回溯
            return false;
        }else{
            return false;
        }

    }
}

//单调递增栈：便于找到离某一索引最近的比自己小的索引处
//单调递减栈：便于找到离某一索引最近的比自己大的索引处

    for(int i = 0;i < len;i++) {
        while(!stack.isEmpty() && heights[stack.peek()] >= heights[i]){
            stack.pop();//单调递增栈：便于找到离某一索引最近的比自己小的索引处
        }
        left[i] = (stack.isEmpty() ? -1 : stack.peek());
        stack.push(i);
    }

84.柱状图中最大的矩形（困难，不会）
法一：直接暴力穷举:枚举宽，双重循环来枚举每种可能的底部宽的组合，循环过程中更新最小高度
——超时

class Solution {
    public int largestRectangleArea(int[] heights) {
        int res = 0,minh = 0;
        int len = heights.length;
        for(int i = 0;i < len;i++){
            minh = heights[i];
            for(int j = i;j < len;j++){
                minh = Math.min(minh,heights[j]);
                res = Math.max(res,(j - i + 1) * minh);
            }
        }
        return res;
    }
}

法二：暴力穷举：枚举高，只需单重循环，当前的柱子即作为矩形的高度，只需获取到俩边低于该处高度的索引即可。——同样超出时间限制。

class Solution {
    public int largestRectangleArea(int[] heights) {
        int res = 0;
        int len = heights.length;
        int left,right;
        for(int i = 0;i < len;i++){
            left = right = i;
            while(left >= 0 && heights[left] >= heights[i]){
                left--;
            }
            
            while(right <= len - 1 && heights[right] >= heights[i]) {
                right++;
            }

            res = Math.max(res,heights[i] * (right - left - 1));
        }
        return res;
    }
}

84.柱状图中最大的矩形
本题正确思路应该是从最大矩形的高度出发，即以每个索引处的矩形高度作为最大矩形的高度来获取左右可延展至的最远处，从而获取宽度。
以每个柱子的高度作为矩形的高度，向俩边延展，
利用单调栈建立索引i处的左右可延展至的最远处索引 left[i] 和right[i]；
本题中，这个栈是个单调递增的栈，

class Solution {
    public int largestRectangleArea(int[] heights) {
        int len = heights.length;
        /计算以每个柱子为最终高度的矩形面积
        /以每个柱子的高度作为矩形的高度，向俩边延展，利用单调栈来获取各柱子左右所能延展至的最远处。
        int[] left = new int[len],right = new int[len];
        // Stack stack = new Stack();
        // Deque stack = new ArrayDeque();
        LinkedList<Integer> stack = new LinkedList();

        for(int i = 0;i < len;i++) {
            while(!stack.isEmpty() && heights[stack.peek()] >= heights[i]){
            /栈不为空并且弹出索引处高度大于当前i处高度，那么还可以继续延展
                stack.pop();
            }
            left[i] = (stack.isEmpty() ? -1 : stack.peek());
            stack.push(i);
            /中间pop的高度都要大于i处，所以后面的只需要和I处比即可，若大于i处高度，那么i处就是最大延展处，
            若小于I处，那么也必然小于这里中间pop的高度。
        }

        stack.clear();

        for(int i = len - 1;i >= 0;i--){
            while(!stack.isEmpty() && heights[stack.peek()] >= heights[i]){
                stack.pop();
            }
            right[i] = (stack.isEmpty() ? len : stack.peek());
            stack.push(i);
        }

        int res = 0;
        for(int i = 0;i < len;i++){
            res = Math.max(res,(right[i] - left[i] - 1) * heights[i]);
        }

        return res;
    }
}

84与85同样是用单调栈来获取某一柱处左右能延展至的最远处left[i]与right[i],从而获取每处所能延展出来的最大矩形。

while(!stack.isEmpty() && heights[stack.peek()] >= heights[i]){
            /栈不为空并且弹出索引处高度大于当前i处高度，那么还可以继续延展
                stack.pop();
            }
            left[i] = (stack.isEmpty() ? -1 : stack.peek());
            stack.push(i);
            /中间pop的高度都要大于i处，所以后面的只需要和I处比即可，若大于i处高度，那么i处就是最大延展处，
            若小于I处，那么也必然小于这里中间pop的高度。

85.最大矩形
将本题按每列或行作为矩形的底部，来按84题思路做解答。
先要创建每列或行的柱状图。
然后按列，进行84题的操作。

class Solution {
    public int maximalRectangle(char[][] matrix) {
        //按列进行84题的最大矩形求解；
        int row = matrix.length,col = matrix[0].length;

        int[][] matrixcol = new int[row][col];
        for(int i = 0;i < row;i++){
            for(int j = 0;j < col;j++){
                if(matrix[i][j] == '1'){
                    matrixcol[i][j] = (j == 0 ? 0 : matrixcol[i][j - 1]) + 1;//创建matrix按列的柱状图
                }
            }
        }

        int len = row;
        int res = 0;

        for(int j = 0;j < col;j++){//对每一列的柱状图进行84题的思路；选取每个柱作为矩形高，左右延展至最远，延展至索引由左右的单调栈来创建left[i]和right[i]
            int[] up = new int[len],down = new int[len];
            LinkedList<Integer> stack = new LinkedList();

            for(int i = 0;i < len;i++){
                while(!stack.isEmpty() && matrixcol[stack.peek()][j] >= matrixcol[i][j]){
                    stack.pop();
                }
                up[i] = stack.isEmpty() ? -1 : stack.peek();
                stack.push(i);
            }
            stack.clear();

            for(int i = len - 1;i >= 0;i--){
                while(!stack.isEmpty() && matrixcol[stack.peek()][j] >= matrixcol[i][j]){
                    stack.pop();
                }
                down[i] = stack.isEmpty() ? len : stack.peek();
                stack.push(i);
            }
            // stack.clear();

            for(int i = 0;i < len;i++){
                res = Math.max(res,(down[i] - up[i] - 1) * matrixcol[i][j]);
            }
        }

        return res;
    }
}

76.最小覆盖子串（难难难！！！）
1.用俩个hashmap记录目标字符串的各字符个数，以及s的滑动窗口的字符数量；
2.用ansl和ansr来记录满足条件的滑动子串的左右边界索引，可以用来获取子串长度，也可以作为最后返回的res结果在s中的索引来使用。3.要注意的是，在滑动窗口找到满足各字符数量不小于目标字符数量的子串时，需要在该滑动窗口内收缩左边界来减小子串长度并更新最小子串，直至不满足条件后再扩展右边界。

class Solution {
    //定义俩个哈希表，分别记录目标字符串和窗洞窗口子串的各字符数量
    private Map<Character,Integer> memot = new HashMap();
    private Map<Character,Integer> memos = new HashMap();
    public String minWindow(String s, String t) {
        int lens = s.length(),lent = t.length();
        for(int i = 0;i < lent;i++){
            char tc = t.charAt(i);
            memot.put(tc,(memot.containsKey(tc) ? memot.get(tc) + 1 : 1));//遍历t来记录目标字符串的各字符数量
        }

        int lenMin = Integer.MAX_VALUE;//用于记录最短子串的长度
        int ansl = -1,ansr = -1;//用于记录符合条件的最短子串的左右边界索引
        int left = 0,right = 0;//定义左右双指针来表示滑动窗口
        while(right < lens){
            if(memot.containsKey(s.charAt(right))){//判断当前字符是否属于目标字符，是的话存入memos，否则跳出本次循环
                memos.put(s.charAt(right),(memos.containsKey(s.charAt(right)) ? memos.get(s.charAt(right)) + 1 : 1));
            }else{
                right++;
                continue;
            }

            while(check()){//判断滑动窗口的memos是否满足memot
                if(lenMin > right - left + 1){//若是更短子串，则更新最短长度和结果子串的左右边界索引
                    lenMin = right - left + 1;
                    ansl = left;
                    ansr = right;
                }
                if(memot.containsKey(s.charAt(left))){
                    memos.put(s.charAt(left), memos.get(s.charAt(left)) - 1);
                }
                left++;//收缩左边界
            }
            right++;
        }

        if(ansl == -1){ return "";}
        return s.substring(ansl,ansr + 1);
    }

    //判断滑动窗口子串的各字符数量是否大于等于目标子串的各字符数量
    public boolean check(){
        for(Map.Entry<Character,Integer> entry : memot.entrySet()){
            if((!memos.containsKey(entry.getKey())) || (memos.get(entry.getKey()) < entry.getValue())){
                return false;//memos不包含对应字符或者数量不足，则返回false
            }
        }
        return true;
    }
}

128.最长连续序列
利用Set记录遍历过的数字；

class Solution {
    private Set<Integer> memo = new HashSet();
    public int longestConsecutive(int[] nums) {
        int len = nums.length;
        int res = Integer.MIN_VALUE;
        for(int i = 0;i < len;i++){
            res = Math.max(res,maxlen(nums[i]));//一边遍历一遍判断
            memo.add(nums[i]);//遍历过后即加入Set
        }
        
        return len == 0 ? 0 : res;
    }

    //maxlen计算memo中左右能延展至的位置，即得长度
    public int maxlen(int cur){
        int left = cur - 1,right = cur + 1;
        while(memo.contains(left)){
            left--;
        }
        while(memo.contains(right)){
            right++;
        }

        return right - left - 1;
    }
}

标准答案：
先用set记录所有元素，然后找不存在num-1的num以其为起始点往左延展，获取最大长度

class Solution {
    public int longestConsecutive(int[] nums) {
        Set<Integer> num_set = new HashSet<Integer>();
        for (int num : nums) {
            num_set.add(num);//先将所有元素添加进HashSet中
        }

        int longestStreak = 0;

        for (int num : num_set) {//遍历Set中的每个元素；以每个元素作为最左边元素进行往右扩展查找最长长度；
        //但是为了剪枝，最长连续数字串必然Set中不存在num-1这个元素，由此来完成剪枝。
            if (!num_set.contains(num - 1)) {
                int currentNum = num;
                int currentStreak = 1;

                while (num_set.contains(currentNum + 1)) {
                    currentNum += 1;
                    currentStreak += 1;
                }

                longestStreak = Math.max(longestStreak, currentStreak);
            }
        }

        return longestStreak;
    }
}

139.单词拆分

class Solution {
    /全排列；回溯,但是会超过时间限制；不过，要是机检的话，可以考虑对极限情况直接输出
    private int lens;
    private int lenw;
    public boolean wordBreak(String s, List<String> wordDict) {
        this.lenw = wordDict.size();
        this.lens = s.length();
        if(lens > 100) return false;//机检的话，可以这样干
        return backtrack(s,wordDict,0);

        // return s.substring(0,0 + wordDict.get(0).length()).equals(wordDict.get(0));
    }

    public boolean backtrack(String s, List<String> wordDict, int start){
        if(start == lens){
            return true;
        }

        for(int i = 0;i < lenw;i++){
            if(start + wordDict.get(i).length() > lens){//长度超出,剪枝
                continue;
            }else if(!(s.substring(start,start + wordDict.get(i).length()).equals(wordDict.get(i)))){//对应位置不一样，剪枝
                continue;
            }

            start += wordDict.get(i).length();
            if(backtrack(s,wordDict,start)){
                return true;
            }
            start -= wordDict.get(i).length();
        }

        return false;
    }
}

正确解答：动态规划
动态规划，只不过状态转移时，遍历wordDict来进行转移判断;
dp数组含义为s前i个字符组成的子串（包含第i个）能否由字符串集合组成

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        /动态规划，只不过状态转移时，遍历wordDict来进行转移判断
        boolean[] dp = new boolean[s.length() + 1];/dp数组含义为s前i个字符组成的子串（包含第i个）能否由字符串集合组成
        dp[0] = true;

        for(int i = 1;i < s.length() + 1;i++){

            for(int j = 0;j < wordDict.size();j++){
                if(wordDict.get(j).length() > i){
                    continue;
                }
                dp[i] = dp[i - wordDict.get(j).length()] && s.substring(i - wordDict.get(j).length(),i).equals(wordDict.get(j));
                if(dp[i] == true){
                    break;
                }
            }

        }

        return dp[s.length()];
    }
}

124.二叉树的最大路径和

/数组的最大子数组和:动态规划，dp[i]表示以i结尾的子串最大和值
 /本题可考虑同样思路，以该节点为起点至子树的最大值
class Solution {
    // private List list = new ArrayList();
    private int resmax = Integer.MIN_VALUE;
    public int maxPathSum(TreeNode root) {
        maxSum(root);
        return resmax;
    }

    public int maxSum(TreeNode node){
        if(node == null){
            return 0;
        }
        int maxl = (node.left == null ? 0 : maxSum(node.left));
        int maxr = (node.right == null ? 0 : maxSum(node.right));
        int res = node.val + (maxl > 0 ? maxl : 0) + (maxr > 0 ? maxr : 0);// 这个是以该节点为根节点的最大和路径
        resmax = Math.max(res,resmax);
        return Math.max(node.val + Math.max(maxl ,maxr),node.val);// 但是返回的应该是以该节点为路径的最大和，则应该是该节点值和左右子树最大和路径较大的那个；
        / 因为这个返回值是用于该节点对其根节点的最大贡献和的值。/即返回包含该节点的最大和
    }
}

146.LRU缓存
哈希表 + 双向链表
创建的双向链表用于实现某一value的最近使用的顺序，以便推出最久未使用value时，直接删除最后一个节点即可。
需要注意，memo存的是key-node。不是key-value；

class LRUCache {
    private int capacity;
    private int size;
    private Map<Integer,DLinkedNode> memo = new HashMap();
    private DLinkedNode head;
    private DLinkedNode tail;


    class DLinkedNode{ / 双向链表，用于记录使用顺序，以便逐出最久未使用的关键字
        int key;
        int value;
        DLinkedNode pre;
        DLinkedNode next;

        public DLinkedNode(){
            
        }

        public DLinkedNode(int key,int value){
            this.key = key;
            this.value = value;
        }

    }

    public void addHead(DLinkedNode node){
        node.pre = head;
        node.next = head.next;
        head.next.pre = node;
        head.next = node;
    }
    public void moveToHead(DLinkedNode node){
        removeNode(node);
        addHead(node);
    }
    public DLinkedNode removeTail(){
        DLinkedNode temp = tail.pre;
        removeNode(temp);
        return temp;
    }
    public void removeNode(DLinkedNode node){
        node.pre.next = node.next;
        node.next.pre = node.pre;
    }
    / 以上为手动创建双向链表及常用方法

    public LRUCache(int capacity) {
        this.capacity = capacity;
        this.size = 0;
        //创建伪首尾节点
        this.head = new DLinkedNode();
        this.tail = new DLinkedNode();
        head.next = tail;
        tail.pre = head;
    }
    
    public int get(int key) {
        DLinkedNode node = memo.get(key);
        if(node == null){   return -1;}
        moveToHead(node);
        return node.value;
    }
    
    public void put(int key, int value) {
        DLinkedNode node = memo.get(key);
        if(node == null){
            DLinkedNode newNode = new DLinkedNode(key,value);
            memo.put(key,newNode);
            addHead(newNode);
            size++;
            if(size > capacity){
                DLinkedNode tail = removeTail();
                memo.remove(tail.key);
                size--;
            }
        }else{
            node.value = value;
            moveToHead(node);
        }
    }
}

148.排序链表
冒泡：双嵌套for循环，每次把最大值放置最后；
选择：双嵌套for循环，每次拿i处与之后所有元素对比，将最小值换至i处；
插入：每次拿i处元素与之前元素对比放置正确位置；
快速：递归+选择分界点（分界点用第一个元素与后续所有对比，小于的放左边，大于的放右边）
归并：中间作为分界点，子组排完序，对俩个排完序的子组进行排序

/冒泡——超时超时超时
class Solution {
    public ListNode sortList(ListNode head) {
        if(head == null){
            return head;
        }
        ListNode nodesize = head;
        int size = 0;
        while(nodesize != null){
            nodesize = nodesize.next;
            size++;
        }
        ListNode node = head;

        while(size > 1){
            node = head;
            for(int i = 1;i < size;i++){
                if(node.val > node.next.val){ //把最大的换至最后
                    int temp = node.val;
                    node.val = node.next.val;
                    node.next.val = temp;
                }
                node = node.next;
            }
            size--;//下次遍历只需要至n- 1即可。
        }
        return head;

    }
}

/ 时间复杂度要求O（nlogn）所以可用归并排序：

/归并排序:时间复杂度要求O（nlogn）
class Solution {
    public ListNode sortList(ListNode head) {
        return sortTwoList(head);
    }

    public ListNode sortTwoList(ListNode node){
        if(node == null || node.next == null){
            return node;
        }

        ListNode node1 = node;
        ListNode node2 = getMid(node);
        node1 = sortTwoList(node1);
        node2 = sortTwoList(node2);
        node = sort(node1,node2);

        return node;
    }

    public ListNode sort(ListNode node1,ListNode node2){
        if(node1 == null){
            return node2;
        }else if(node2 == null){
            return node1;
        }
        / 合并俩个有序链表
        if(node1.val > node2.val){
            node2.next = sort(node1,node2.next);
            return node2;
        }else{
            node1.next = sort(node1.next,node2);
            return node1;
        }
        
    }

    public ListNode getMid(ListNode node){
    / 快慢双指针确定中点
        ListNode slow = node,fast = node.next;
        while(fast != null && fast.next != null){
            slow = slow.next;
            fast = fast.next.next;
        }
        fast = slow.next;
        slow.next = null;
        return fast;
    }
}

152.乘积最大子数组

class Solution {
    / 本题与最大和的子数组不同；本题有正负之分。
    public int maxProduct(int[] nums) {
        int len = nums.length;
        int[] dpmin = new int[len],dpmax = new int[len];/ 以i结尾的最大/最小乘积子数组
        dpmin[0] = nums[0];
        dpmax[0] = nums[0];

        for(int i = 1;i < len;i++){ / 遍历对nums[i]正负进行分类讨论;自身，自身为正与前者乘积，自身为负与前者乘积
            dpmax[i] = Math.max((nums[i] * dpmin[i - 1]),Math.max(nums[i],nums[i] * dpmax[i - 1])); 
            dpmin[i] = Math.min(nums[i],Math.min(nums[i] * dpmin[i - 1],nums[i] * dpmax[i - 1]));
        }

        int res = Integer.MIN_VALUE;
        for(int i = 0;i < len;i++){
            res = Math.max(res,dpmax[i]);
        }

        return res;

    }
}

155.最小栈

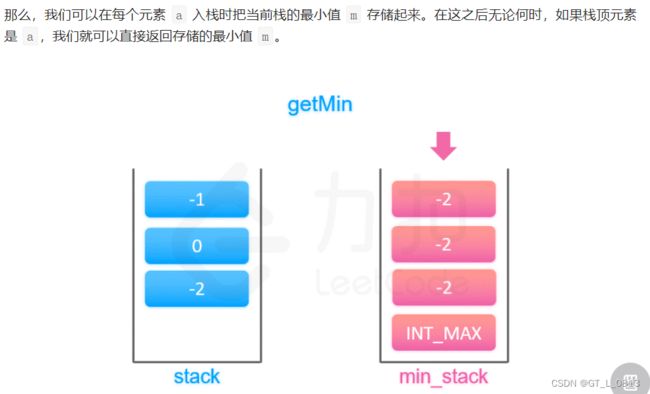
class MinStack {
    private Stack<Integer> stack,minStack;
    // private int minValue = Integer.MAX_VALUE;

    public MinStack() { / 利用辅助栈来随栈stack记录最小值；
        stack = new Stack();
        minStack = new Stack();
        minStack.push(Integer.MAX_VALUE);
    }
    
    public void push(int val) {
        stack.push(val);
        // minValue = Math.min(minValue,val);
        minStack.push(Math.min(val,minStack.peek()));/ 当前push的值应与之前的最小值对比后push入最小栈
    }
    
    public void pop() {
        stack.pop();
        minStack.pop();
    }
    
    public int top() {
        return stack.peek();
    }
    
    public int getMin() {
        return minStack.peek();
    }
}

169.多数元素

class Solution {
    public int majorityElement(int[] nums) {
        / 哈希表记录所有元素个数
        // Map memo = new HashMap();
        // int len = nums.length;
        // int res = Integer.MAX_VALUE;
        // memo.put(res,0);

        // for(int i = 0;i < nums.length;i++){
        //     memo.put(nums[i],memo.containsKey(nums[i]) ? memo.get(nums[i]) + 1 : 1);
        //     // if(memo.get(nums[i]) > len/2){  return nums[i];}
        //     res = memo.get(nums[i]) > memo.get(res) ? nums[i] : res;
        // }
        // return res;

        / 先排序，则处于n / 2索引处的即为多数元素
        Arrays.sort(nums);
        return nums[nums.length / 2];
    }
}

207.课程表
判断拓扑图是否有环，则可以在每条路上都走上一遍来看看是否会走到重复的节点

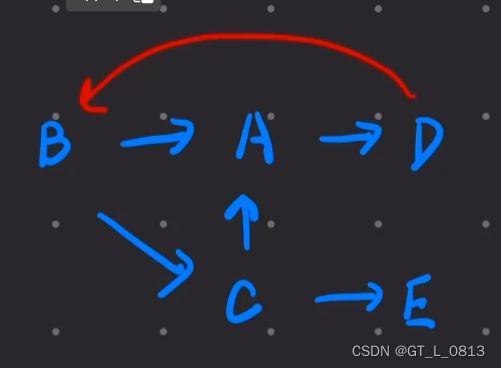
/ 深度优先 + 有向图查找环 + visited剪枝
class Solution {
    private int[] visited;
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        int row = prerequisites.length,col = 2;
        
        //构建有向图；方向前面的作索引，后面的作list的值
        List<ArrayList<Integer>> graph = new ArrayList();
        for(int i = 0;i < numCourses;i++){
            graph.add(new ArrayList<Integer>());
        }
        for(int i = 0;i < row;i++){
            graph.get(prerequisites[i][1]).add(prerequisites[i][0]);//以前提课程为索引，要学课程为值加入list；
        }
        
        visited = new int[numCourses];//0表示未走过；1表示走过；2表示走过且无环；
        for(int i = 0;i < numCourses;i++){
            if(isCircle(graph,visited,i)){/ 从每个索引的起点开始进行有向图有无环的判断
                return false;
            }
        }
        return true;
    }

    public boolean isCircle(List<ArrayList<Integer>> graph,int[] visited,int start){
        if(visited[start] == 1){ // 1表示已经走过了，故形成了环
            return true;
        }
        if(visited[start] == 2){//无环剪枝进行优化，避免超时
            return false;
        }

        visited[start] = 1;
        for(int startson : graph.get(start)){
            if(isCircle(graph,visited,startson)){
                return true;
            }
        }
        visited[start] = 2;/ 表示当前start开始的经过for循环没有环，故设置为2表示该节点起始无环

        return false;
    }
}

208.实现Trie(前缀树)

class Trie {
    //字典树
    private Trie[] children;
    private boolean isend;
    private Trie head;/头节点

    public Trie() {
        children = new Trie[26];/ 即每个节点其实都可以有26个索引可以指向下一个节点；只不过这26个索引需要有值不为null才行；索引即表示了字符
        // isend = false;// 默认为false
        head = this;
    }
    
    public void insert(String word) {
        Trie node = head;
        for(int i = 0;i < word.length();i++){
            int index = word.charAt(i) - 'a';/判断第一个节点是否有word.charAt(i)这个字符
            if(node.children[index] == null){
                node.children[index] = new Trie(); / 创建word.charAt(i)这个字符的字典树
            }
            node = node.children[index];
        }
        node.isend = true; / 表示这个节点结尾是一个字符串
    }
    
    public boolean search(String word) {
        Trie node = head;
        for(int i = 0;i < word.length();i++){
            int index = word.charAt(i) - 'a';
            if(node.children[index] == null){
                return false;
            }
            node = node.children[index];
        }
        return node.isend;// 判断是否为叶子节点
    }
    
    public boolean startsWith(String prefix) {
        Trie node = head;
        for(int i = 0;i < prefix.length();i++){
            int index = prefix.charAt(i) - 'a';
            if(node.children[index] == null){
                return false;
            }
            node = node.children[index];
        }
        return true;
    }
}

221.最大正方形

class Solution {
    / 1.暴力法 
    public int maximalSquare(char[][] matrix) {
        int res = Integer.MIN_VALUE;
        int row = matrix.length,col = matrix[0].length;
        int maxSide = 0;
        for(int i = 0;i < row;i++){
            for(int j = 0;j < col;j++){
                if(matrix[i][j] == '1'){
                    maxSide = Math.min(matrix.length - i,matrix[0].length - j);/ 按照行列获取可能的最大边长
                    maxSide = getMinSide(matrix,i,j,maxSide);/ 递归找出为'0'的元素索引从而更新maxside
                    res = Math.max(res,maxSide * maxSide);
                }
            }
        }
        return res == Integer.MIN_VALUE ? 0 : res;
    }

    public int getMinSide(char[][] matrix, int is, int js, int maxSide){
        for(int i = 0;i < maxSide;i++){
            for(int j = 0;j < maxSide;j++){
                if(matrix[is + i][js + j] == '0'){
                    maxSide = Math.max(i,j);
                    return getMinSide(matrix,is,js,maxSide);
                }
            }
        }
        return maxSide;
    }
}

// 2.动态规划
dp[i][j]:表示以（i，j）处为正方形右下角的最大边长
下方状态转移方程记住即可。

class Solution {
    public int maximalSquare(char[][] matrix) {
        int row = matrix.length,col = matrix[0].length;
        int maxSide = 0;
        int[][] dp = new int[row + 1][col + 1];//表示以i，j为正方形右下角的最大边长
        for(int k = 0;k < row + 1;k++){
            dp[k][0] = 0;
        }
        for(int k = 0;k < col + 1;k++){
            dp[0][k] = 0;
        }

        for(int i = 1;i < row + 1;i++){
            for(int j = 1;j < col + 1;j++){
                if(matrix[i - 1][j - 1] == '1'){
                    dp[i][j] = Math.min(dp[i - 1][j - 1],Math.min(dp[i][j - 1],dp[i - 1][j])) + 1;
                    /状态转移矩阵，背下来即可，证明就算了
                    maxSide = Math.max(maxSide,dp[i][j]);
                } 
            }
        }   
        return maxSide * maxSide;
    }
}

238.除自身以外数组的乘积

class Solution {
    //answer[i]等于nums 中除 nums[i] 之外其余各元素的乘积
    //也可理解为nums[i]前元素乘积与后元素乘积的乘积
    public int[] productExceptSelf(int[] nums) {
        int len = nums.length;
        / 构造前缀积数组与后缀积数组，用于求解res
        int[] ltor = new int[len],rtol = new int[len],res = new int[len];
        ltor[0] = nums[0];
        rtol[len - 1] = nums[len - 1];
        for(int i = 1;i < len;i++){
            ltor[i] = ltor[i - 1] * nums[i];
        }
        for(int i = len -2;i >= 0;i--){
            rtol[i] = rtol[i + 1] * nums[i];
        }

        res[0] = rtol[1];
        res[len - 1] = ltor[len - 2];
        for(int i = 1;i < len - 1;i++){
            res[i] = ltor[i - 1] * rtol[i + 1];
        }
        return res;
    }
}

优化内存：则res作为rtol;然后从右往左遍历时，用一个变量R记录后面元素乘积
class Solution {
    //answer[i]等于nums 中除 nums[i] 之外其余各元素的乘积
    //也可理解为nums[i]前元素乘积与后元素乘积的乘积
    public int[] productExceptSelf(int[] nums) {
        int len = nums.length;
        int[] res = new int[len];
        res[0] = 1;
        // res[1] = nums[0];//先算res[i]表示nums[i]前的元素乘积
        for(int i = 1;i < len;i++){
            res[i] = res[i - 1] * nums[i - 1]; //nums[i]前的元素乘积
        }

        int R = 1;
        for(int i = len - 2;i >= 0;i--){
            R *= nums[i + 1];
            res[i] = res[i] * R;
        }
        return res;
    }
}

239.滑动窗口最大值

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if(k == 1){
            return nums;
        }

        int len = nums.length;
        int[] res = new int[len - k + 1];

        / 因为这里优先队列存放的是引用类型，那么remove时new的对象是新地址，无法删除。考虑用memo记录key对应的int[]对象地址用于优先队列的移除
        Map<Integer,int[]> memo = new HashMap();
        PriorityQueue<int[]> maxQueue = new PriorityQueue<int[]>(new Comparator<int[]>(){
            @Override
            public int compare(int[] m,int[] n){
                return n[1] - m[1];
            }
        });
        for(int i = 0;i < k;i++){
            int[] indexValue = new int[]{i,nums[i]};
            memo.put(i,indexValue);
            maxQueue.offer(indexValue);
        }
        res[0] = maxQueue.peek()[1];

        for(int i = k;i < len;i++){
            maxQueue.remove(memo.get(i - k));
            int[] indexValue = new int[]{i,nums[i]};
            memo.put(i,indexValue);
            maxQueue.offer(indexValue);
            res[i - k + 1] = maxQueue.peek()[1];
        }

        return res;
    }
}
/ 该方法思路没错，就是用优先队列来维护滑动窗口中的有序元素以及索引值，所以存int[]类型，但是超时，这是因为每次窗口移动需要删除前面的一个int[]元素；我这里用了memo来记录索引对应的int[]用于优先队列进行删除。
但其实不需要删除，只需要获取最大值时，将优先队列的最大值peek出来，判断索引是否还在窗口内，不在的话就poll了，直到peek的索引在窗口内，才获取当前res值。

class Solution {
    public int[] maxSlidingWindow(int[] nums, int k) {
        if(k == 1){
            return nums;
        }
        int len = nums.length;
        int[] res = new int[len - k + 1];

        PriorityQueue<int[]> maxQueue = new PriorityQueue<int[]>(new Comparator<int[]>(){
            @Override
            public int compare(int[] m,int[] n){
                return n[1] - m[1];
            }
        });
        for(int i = 0;i < k;i++){
            maxQueue.offer(new int[]{i,nums[i]});
        }
        res[0] = maxQueue.peek()[1];

        for(int i = k;i < len;i++){
            maxQueue.offer(new int[]{i,nums[i]});
            int[] numQueue = maxQueue.peek();
            while(numQueue[0] < i - k + 1){ /判断当前优先队列的最大值的索引是否还在窗口内
                maxQueue.poll();
                numQueue = maxQueue.peek();
            }
            res[i - k + 1] = numQueue[1];
        }

        return res;
    }
}

279.完全平方数

class Solution {
    / 题意是找出符合答案的最少数量，不要求将子集或者排列返回；所以考虑使用动态规划。
    / 而且本题类似背包问题，即向容器中添加元素
    public int numSquares(int n) {
        int num = (int)Math.sqrt(Double.valueOf(n));/获取可选元素，即可选物品
        int[][] dp = new int[num + 1][n + 1];/ dp[i][j]表示1-i的元素，j的容积，和为n的完全平方数的最少数量
        for(int k = 0;k <= num;k++){
            dp[k][0] = 0;
        }
        for(int k = 1;k <= n;k++){
            dp[0][k] = Integer.MAX_VALUE;/ 0个可选元素，要装满k，故需要在后续对比中选择其它值
        }

        for(int i = 1;i <= num;i++){
            for(int j = 1;j <= n;j++){
                / 当前可选元素超过背包的分类讨论
                if(Math.pow(i,2) > j){
                    dp[i][j] = dp[i - 1][j];
                }else{
                    / 分类：i处元素是否使用。取较小者
                    dp[i][j] = Math.min(dp[i - 1][j],1 + dp[i][j - (int)Math.pow(i,2)]);
                }
            }
        }
        return dp[num][n];
    }
}

class Solution {
    public int numSquares(int n) {
        int num = (int)Math.sqrt(Double.valueOf(n));/ 开方确定所能选择的数字范围。
        int[] dp = new int[n + 1];/ 数字i所需要的最少数
        dp[0] = 0;
        dp[1] = 1;
        for(int i = 2;i < n + 1;i++){
            dp[i] = Integer.MAX_VALUE;
            for(int addN = 1;addN <= num;addN++){
                if(addN * addN > i){
                    break;
                }
                dp[i] = Math.min(dp[i - addN * addN] + 1,dp[i]);//动态规划
            }
        }

        return dp[n];
    }
}

287.寻找重复数—数组使用快慢双指针，以slow = nums[slow];fast = nums[nums[fast]];

class Solution {
    public int findDuplicate(int[] nums) {
        // int res = nums.length;
        int slow = 0,fast = 0;/ 以nums[i]的值表示指针来指向对应索引处的nums[nums[i]];双链表判断是否有环
        do{
            slow = nums[slow];
            fast = nums[nums[fast]];
        }while(slow != fast);

        fast = 0;
        while(slow != fast){
            slow = nums[slow];
            fast = nums[fast];
        }

        return fast;
    }
}

406.根据身高重建队列

class Solution {
    / 先按身高排序；然后往res里按顺序放，放的同时要考虑在前面预留k个空位给比自己个子高的人
    public int[][] reconstructQueue(int[][] people) {
        int row = people.length;
        Arrays.sort(people,new Comparator<int[]>(){
            @Override
            public int compare(int[] m,int[] n){/排序时，若身高相等，则需要先插入res中那个更靠后的，因为要预留足够的位置
                if(m[0] != n[0]){
                    return m[0] - n[0];
                }else{
                    return n[1] - m[1];
                }
            }
        });
        
        int[][] res = new int[row][];
        for(int[] r : people){
            int space = r[1];
            for(int i = 0;i < row;i++){
                if(space == 0 && res[i] == null){ 
                    res[i] = r;
                    break;
                }else if(res[i] == null){
                    space--;
                }
            }
        }
        return res;
    }
}

437.路径总和Ⅲ

/双递归
class Solution {
    public int pathSum(TreeNode root, int targetSum) {
        if(root == null){   return 0;}
        int num = curPaths(root,targetSum);
        return num + pathSum(root.left,targetSum) + pathSum(root.right,targetSum);/递归求每一个节点为起点的路径数
    }

    /定义以root为起点的符合题意的路径总数求解递归函数
    public int curPaths(TreeNode root,int targetSum){
        if(root == null){
            return 0;
        }

        int l = curPaths(root.left,targetSum - root.val);
        int r = curPaths(root.right,targetSum - root.val);

        return targetSum == root.val ? 1 + l + r : l + r;
    }
}

617.合并二叉树

class Solution {
    public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
        if(root1 == null){
            return root2;
        }else if(root2 == null){
            return root1;
        }/ 处理有一个节点为空的情况
        TreeNode root = new TreeNode(root1.val + root2.val);/ 处理俩节点覆盖的情况
        root.left = mergeTrees(root1.left,root2.left);
        root.right = mergeTrees(root1.right,root2.right);

        return root;
    }
}

494.目标和

class Solution {
    //1.回溯//2.动态规划(容器、背包问题)
    private int res,len;
    public int findTargetSumWays(int[] nums, int target) {
        //回溯
        this.len = nums.length;
        backtrack(nums,target,0);

        return res;
    }

    public void backtrack(int[] nums,int target,int curIndex){
        if(curIndex >= len){
            if(target == 0){
                res++;
            }
            return;
        }
        backtrack(nums,target - nums[curIndex],curIndex + 1);
        backtrack(nums,target + nums[curIndex],curIndex + 1);
        return;
    }
}

581.最短无序连续子数组
可以先作一个排完序的数组，然后俩者左右对比至首次不同处，即为要进行排序的地方

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int len = nums.length;
        int[] temp = Arrays.copyOf(nums,len);
        Arrays.sort(temp);
        int i = 0,j = len - 1;
        while(i < len && nums[i] == temp[i]){
            i++;
        }
        if(i >= len){
            return 0;
        }
        while(nums[j] == temp[j]){
            j--;
        }
        return j - i + 1;
    }
}

一次遍历：


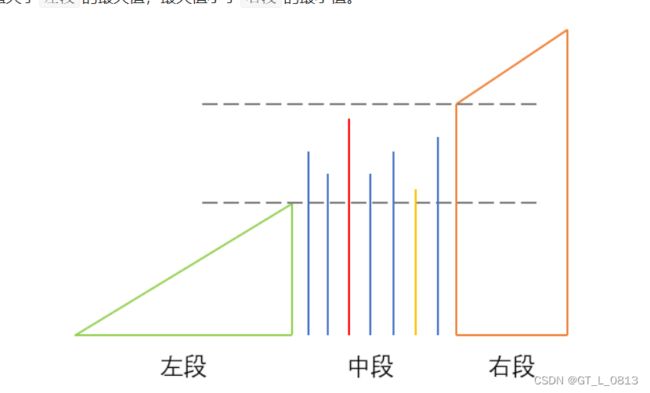
右边界必然nums[i - 1]>nums[i]；左边界必然nums[i]>nums[i + 1]
所以为确定右边界，可以从左往右遍历保存最后一个nums[i - 1]>nums[i]；同理获取左边界。

class Solution {
    public int findUnsortedSubarray(int[] nums) {
        int len = nums.length;
        int left = -1,right = -1;//左右指针，遍历时更新左小右大
        int maxR = Integer.MIN_VALUE,minL = Integer.MAX_VALUE;
        for(int i = 0;i < len;i++){/ 一次遍历过程中进行numsB的左右边界更新；右边界必然nums[i - 1]>nums[i]；左边界必然nums[i]>nums[i + 1]
            if(nums[i] < maxR){
                right = i;/ 当前值小于之前的最大值，故更新右边界
            }else{
                maxR = nums[i];
            }

            if(nums[len - i - 1] > minL){
                left = len - i - 1;/ 当前值大于之前的最小值，故更新左边界
            }else{
                minL = nums[len - i - 1];
            }
        }
        return left == -1 ? 0 : right - left + 1;
    }
}

647.回文子串

class Solution {
    /动态规划：回文子串去除俩头仍是回文子串；
    /dp[][]数组用于各子串判断是否为回文子串，然后结果统计所有为TRUE的元素
    public int countSubstrings(String s) {
        int len = s.length();
        boolean[][] dp = new boolean[len][len];
        int res = 0;

        for(int i = len - 1;i >= 0;i--){
            for(int j = i;j < len;j++){
                if(i == j){
                    dp[i][j] = true;
                }else if(j - i == 1){
                    dp[i][j] = (s.charAt(i) == s.charAt(j) ? true : false);
                }else{
                    dp[i][j] = (s.charAt(i) == s.charAt(j) ? dp[i + 1][j - 1] : false);
                }
                if(dp[i][j] == true){
                    res++;
                }
            }
        }

        return res;
    }
}

739.每日最高温度（同84，85俩道最大矩形的困难题，用到了单调栈）

class Solution {
    /单调栈；上一次用是在求最大矩形，用单调栈求当前柱左右可延展的最远处。是找第一个小于该柱高度的索引，用的是单调递增的栈
    /这里要找下一个高于该处高度的索引，单调递减的栈
    public int[] dailyTemperatures(int[] temperatures) {
        int len = temperatures.length;
        int[] res = new int[len];
        Stack<Integer> stack = new Stack();/单调栈用于存储索引以便获取长度

        int k = len - 1;
        while(k >= 0){
            while(!stack.empty() && temperatures[stack.peek()] <= temperatures[k]){
                stack.pop();
                /栈不为空，找到比当前元素大的索引，前面小于当前值的索引可弹出，因为我们会在后面push进栈当前值
            }
            res[k] = stack.empty() ? 0 : stack.peek() - k;
            stack.push(k);
            /k处的值要大于之前被弹出的值，故保留这里的值既可用于前面寻找第一个大于元素的最近索引；这里的最近也就说明了后面小于k处的值索引就可以pop了
            k--;
        }
        
        return res;
    }
}