多层感知机的反向传播算法

1 基本概念

前向传播

多层感知机中，输入信号通过各个网络层的隐节点产生输出的过程称为前向传播。

图形化表示

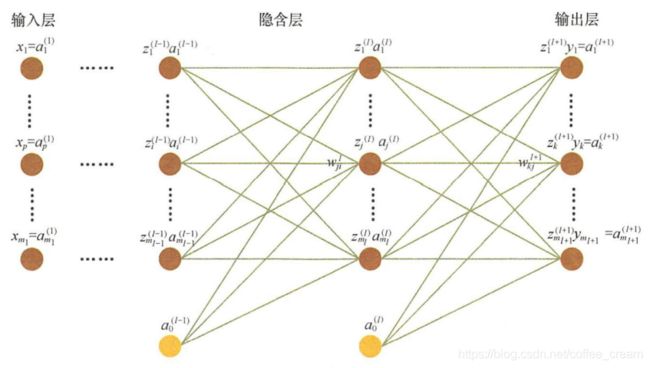
下图展示了一个典型的多层感知机

• 定义第 $(l)$ 层的输入为 $x^{(l)}$
• 在每一层中
  • 首先利用输入 $x^{(l)}$ 计算仿射变换 $z^{(l)}=W^{(l)}{x}^{(l)}+b^{(l)}$
  • 然后激活函数 $f$ 作用于 $z^{(l)}$，得到 $a^{(l)}=f(z^{(l)})$
  • $a^{(l)}$ 直接作为下一层的输入，即 $x^{(l+1)}$

设 $x^{(l)}$ 为 $m$ 维向量，$z^{(l)}$ 和 $a^{(l)}$ 为 $n$ 维向量，则 $W^{(l)}$ 为 $m\times n$ 维的矩阵，这里分别用 $z_i^{(l)}$ 、$a_i^{(l)}$ 和 $W_{ij}^{(l)}$ 表示其中的一个元素。

反向传播算法

在网络训练中，前向传播最终产生一个标量损失函数。
反向传播算法（ Back Propagation ） 则将损失函数的信息沿网络层向后传播用以计算梯度，达到优化网络参数的目的。反向传播算法是多层神经网络有监督训练中最简单也最一般的方法之一。

2 多层感知机的损失函数

给定包含 $m$ 个样本的集合 $\{(x^{(1)},y^{(1)}),\cdots ,(x^{(m)},y^{(m)}\}$，假设多层感知机的层数（layer）为 $N$，在第 $l$ 层的神经节点数目为 $s_l$

2.1 平方误差损失函数

$$\begin{array}{rl}J(W,b)& =[\frac{1}{m}\sum _{i=1}^{m}J(W,b;x^{(i)},y^{(i)})]+\frac{\lambda }{2}\sum _{l=1}^{N-1}\sum _{i=1}^{s_l}\sum _{j=1}^{s_l+1}(W_{ij}^{(l)}{)}^2\\ & =[\frac{1}{m}\sum _{i=1}^m\frac{1}{2}\Vert y^{(i)}-f_{w,b}(x^{(i)}){\Vert }^2]+\frac{\lambda }{2}\sum _{l=1}^{N-1}\sum _{i=1}^{s_l}\sum _{j=1}^{s_{(l+1)}}(W_{ij}^{(l)}{)}^2\end{array}$$

• 第一项为平方误差项；
• 第二项为 L2 正则化项，在功能上可以称作权重衰减项，目的是减少权重的幅度，防止过拟合，其中 $W_{ij}^{(l)}$ 指的是第 $l$ 层神经网络上的第 $i$ 节点到第 $l+1$ 层神经网络上的第 $j$ 个节点的权重；
• 第二项前面的系数 $\lambda$ 为权重衰减参数，用于控制损失函数中两项的相对权重。

2.2 交叉熵损失函数

以二分类场景为例，交叉熵损失函数定义为：

$$\begin{array}{rl}J(W,b)& =-[\frac{1}{m}\sum _{i=1}^{m}J(W,b;x^{(i)},y^{(i)})]+\frac{\lambda }{2}\sum _{l=1}^{N-1}\sum _{i=1}^{s_l}\sum _{j=1}^{s_l+1}(W_{ij}^{(l)}{)}^2\\ & =-[\frac{1}{m}\sum _{i=1}^m\{y^{(i)}\ln o^{(i)}+(1-y^{(i)})\ln (1-o^{(i)})\}]+\frac{\lambda }{2}\sum _{l=1}^{N-1}\sum _{i=1}^{s_l}\sum _{j=1}^{s_{(l+1)}}(W_{ij}^{(l)}{)}^2\end{array}$$

• 正则项与平方误差损失函数中的相同；
• 第一项衡量了预测 $o^{(i)}$ 与真实类别 $y^{(i)}$ 之间的交叉熵，当 $y^{(i)}$ 与 $o^{(i)}$ 相同时，损失函数达到最小

在多分类中，其相应的损失函数为：

$$J(W,b)=-[\frac{1}{m}\sum _{i=1}^m\sum _{k=1}^n{y}_k^{(i)}\ln o_k^{(i)}]+\frac{\lambda }{2}\sum _{l=1}^{N-1}\sum _{i=1}^{s_l}\sum _{j=1}^{s_l+1}(W_{ij}^{(l)}{)}^2$$

• $o_k^{(i)}$ 代表第 $i$ 个样本的预测属于类别 $k$ 的概率
• $y_k^{(i)}$ 为实际概率（如果第 $i$ 个样本的真实类别为 $k$，则 $y_k^{(i)}=1$，否则为 0）

2.3 平方误差损失函数和交叉熵损失函数分别适合什么场景

一般来说：

• 平方误差损失函数更适合输出为连续、并且最后一层不含 Sigmoid 或 Softmax 函数的神经网络；
• 交叉熵损失则更适合二分类或多分类的场景。

想正确回答出答案也许并不难， 但是要想给出具有理论依据的合理原因，还需要对它们的梯度推导熟悉掌握，并且具备一定的灵活分析能力。（推导见下一节）

为何平方损失函数不适合最后一层含有 Sigmoid Sofmax 激活函数的神经网络呢？

平方误差损失函数相对于输出层的导数为：

$${\delta }^{(L)}=-(y-a^{(L)})f^{\prime }(z^{(L)})$$

其中最后一项 $f^{\prime }(z^{(L)})$ 为激活函数的导数。

当激活函数为 Sigmoid 函数时，如果 $z^{(L)}$ 的绝对值较大，函数的梯度会趋于饱和，即 $f^{\prime }(z^{(L)})$ 的绝对值非常小，导致 ${\delta }^{(L)}$ 的取值也非常小，使得基于梯度的学习速度非常缓慢。

而当使用交叉摘损失函数时，相对于输出层的导数（也可以被认为是残差）为

$${\delta }^{(L)}=f(z_{\hat{k}}^{(L)})-1=a_{\hat{k}}^{(L)}-1$$

此时的导数是线性的，因此不会存在学习速度过慢的问题。

3 推导各层参数更新的梯度计算公式

令:

• 第 $(l)$ 层的参数为 $W^{(l)}$ 和 $b^{(l)}$
• 每层的线性变换为 $z^{(l)}=W^{(l)}{x}^{(l)}+b^{(l)}$
• 输出为 $a^{(l)}=f(z^{(l)})$，其中 $f$ 为非线性激活函数（如 Sigmod、Tanh、ReLU 等）
• $a^{(l)}$ 直接作为下一层的输入，即 $x^{(l+1)}=a^{(l)}$

我们可以用批量梯度下降法来优化网络参数，梯度下降法中每次对参数 $W$（网络连接权重）和 $b$（偏置）进行更新：

$$\begin{array}{rl}{W}_{ij}^{(l)}& =W_{ij}^{(l)}-\alpha \frac{\partial }{\partial W_{ij}^{(l)}}J(W,b)\\ b_i^{(l)}& =b_i^{(l)}-\alpha \frac{\partial }{\partial b_i^{(l)}}J(W,b)\end{array}$$

其中，$\alpha$ 为学习率，控制每次迭代中梯度变化的幅度。

从上面的式子可以看出，问题的核心就是求解 $\frac{\partial }{\partial W_{ij}^{(l)}}J(W,b)$ 和 $\frac{\partial }{\partial b_i^{(l)}}J(W,b)$。

---

损失函数对隐含层的偏导

为了得到递推公式，我们需要计算损失函数对隐含层的偏导

$$\frac{\partial }{\partial z_i^{(l)}}J(W,b)=\sum _{j=1}^{s_{l+1}}(\frac{\partial J(W,b)}{\partial z_j^{(l+1)}}\frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}})$$

其中，$s_{l+1}$ 为第 $l+1$ 层的节点数，而

$$\frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}}=\frac{\partial (W_{ij}^{(l)}{x}^{(l+1)}+b_j^{(l+1)})}{\partial z_i^{(l)}})$$

其中，$b^{(l)}$ 与 $z_i^{(l)}$ 无关可以省去，$x^{l+1}=a^l=f(z^{(l)})$，因此，上式可以写作：

$$\frac{\partial z_j^{(l+1)}}{\partial z_i^{(l)}}=W_{ij}^{(l)}{f}^{\prime }(z_i^{(l)})$$

$\frac{\partial }{\partial z_i^{(l)}}J(W,b)$ 可以看作是损失函数在第 $l$ 层第 $i$ 个节点产生的残差值，记为 ${\delta }_i^{(l)}$，推导公式就可以表示为：

$${\delta }_i^{(l)}=(\sum _{j=1}^{s_{l+1}}{W}_{ij}^{(l)}{\delta }_j^{(l+1)})f^{\prime }(z_i^{(l)})$$

---

损失函数对参数函数的梯度就可以写为：

$$\begin{array}{rl}\frac{\partial }{\partial W_{ij}^{(l)}}J(W,b)& =\frac{\partial J(W,b)}{\partial z_j^{(l+1)}}\frac{\partial z_j^{(l+1)}}{\partial W_{ij}^{(l)}}\\ & ={\delta }_i^{(l+1)}{x}_j^{(l+1)}\\ & ={\delta }_i^{(l+1)}{a}_j^{(l)}\\ \frac{\partial }{\partial b_i^{(l)}}J(W,b)& ={\delta }_i^{(l+1)}\end{array}$$

从上式中可以看出，利用 $(l+1)$ 层在第 $i$ 个节点产生的残差值 ${\delta }_i^{(l+1)}$，就可以对第 $l$ 层的 $W_{ij}^{(l)}$ 与 $b_i^{(l)}$ 进行更新。

因此，反向传播算法的步骤可以写为：

• 利用前向传到公式，得到从第 1 层到第 $L$ 层的输出值
• for $l=L\to 1$
  • 计算第 $l$ 层的残差 ${\delta }_i^{(l)}$
  • 得到 $\frac{\partial }{\partial W_{ij}^{(l)}}J(W,b)$ 与 $\frac{\partial }{\partial b_i^{(l)}}J(W,b)$
  • 对 $W_{ij}^{(l)}$ 与 $b_i^{(l)}$ 进行更新

其中，根据选择的损失函数不同，${\delta }_i^{(L)}$ 的计算也不相同，为了简化，这里忽略 Batch 样本集合和正则化项的影响，重点关注两种损失函数产生的梯度

• 平方误差损失函数
  $$\begin{array}{rl}J(W,b)& =\frac{1}{2}\Vert y-a^{(L)}{\Vert }^2\\ & =\frac{1}{2}\Vert y-f(z^{(L)}){\Vert }^2\\ {\delta }^{(L)}& =-(y-a^{(L)})f^{\prime }(z^{(L)})\end{array}$$

• 交叉熵损失函数
  $$\begin{array}{rl}J(W,b)& =-\sum _{k=1}^n{y}_k\ln a_k^{(L)}\\ & =-\sum _{k=1}^n{y}_k\ln f(z_k^{(L)})\end{array}$$

在分类问题中，$y_k$ 仅在一个类别$k$ 时取1，其余为 0，令实际的类别为 $\hat{k}$，则

$$\begin{array}{rl}J(W,b)& =-\ln a_{\hat{k}}^{(L)}\\ {\delta }^{(L)}& =-\frac{f^{\prime }(z_{\hat{k}}^{(L)})}{f(z_{\hat{k}}^{(L)})}\end{array}$$

当 $f$ 取 SoftMax 激活函数时，$f^{\prime }(x)=f(x)(1-f(x))$，则有：

$${\delta }^{(L)}=f(z_{\hat{k}}^{(L)})-1=a_{\hat{k}}^{(L)}-1$$

4 反向传播算法中最重要的四个公式

根据上一节的推导，可以得到下面几个公式

（1）损失函数在第 $L$ 层第 $i$ 个节点的误差

$$\begin{array}{rl}{\delta }_i^{(L)}& =\frac{\partial }{\partial z_i^L}J(W,b)\\ & =\sum _{k=1}^{s_L}\frac{\partial J(W,b)}{\partial a_k^L}\frac{\partial a_k^L}{\partial z_i^L}\\ & =\frac{\partial J(W,b)}{\partial a_i^L}\frac{\partial a_i^L}{\partial z_i^L}\\ & =\frac{\partial J(W,b)}{\partial a_i^L}{f}^{\prime }(z_i^{(L)})\end{array}$$

（2）根据第 $l+1$ 层的误差来计算第 $l$ 层的误差

$${\delta }_i^{(l)}=(\sum _{j=1}^{s_{l+1}}{W}_{ij}^{(l)}{\delta }_j^{(l+1)})f^{\prime }(z_i^{(l)})$$

（3）根据每层上每个神经元上的误差来计算参数偏置 $b_i^l$ 的梯度下降方向

$$\frac{\partial }{\partial b_i^{(l)}}J(W,b)={\delta }_i^{(l+1)}$$

（4）根据每层上每个神经元上的误差来计算参数权重 $w_i^l$ 的梯度下降方向

$$\frac{\partial }{\partial W_{ij}^{(l)}}J(W,b)={\delta }_i^{(l+1)}{a}_j^{(l)}$$