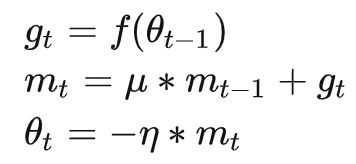数据分析-深度学习Pytorch Day11

首先要搞懂损失函数与代价函数。

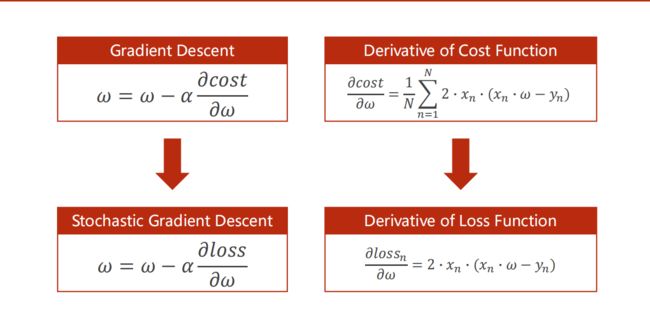
损失函数是单个样本与真实值之间的差距

代价函数是整个样本集与真实值的平均差距

随机梯度下降就是不使用代价函数对参数进行更新，而是使用损失函数对参数更新。

梯度下降法( gradient descent )是一阶最优化算法，通常也称为最速下降法，是通过函数当前点对应梯度(或者是近似梯度)的反方向，使用规定步长距离进例行迭代搜索，从而找到一一个函数的局部极小值的算法，最好的情况是希望找到全局极小值。但是在使用梯度下降算法时，每次更新参数都需要使用所有的样本。如果 对所有的样本均计算一次， 当样本总量特别大时,对算法的速度影响非常大，所以就有了随机梯度下降(stochastic gradient descent, SGD )算法。它是对梯度下降法算法的一种改进，且每次只随机取一部分样本进行优化， 样本的数量一般是2的整数次幂，取值范围是32~256,以保证计算精度的同时提升计算速度，是优化深度学习网络中最常用的一类算法。

SGD算法及其一些变种， 是深度学习中应用最多的一类算法。在深度学习中，SCD通常指小批随机梯度下降( mini-batch gradient descent )算法，其在训练过程中，通常会使用一个固定的学习率进行训练。 即

gt是梯度， n是学习率，学习率用来调整梯度影响大小，梯度完全依赖于batch得到的数据

由于随机梯度下降算法的缺点，动量的思想被加入到算法中：动量通过模拟物体运动的方向，在更新时会在一定程度上考虑之前参数更新的大小和方向，同时利用batch计算得到的梯度，两者结合起来计算出最终参数的大小以及方向，引入动量之后，参数更新方式为：

mt是当前动量的累加， u 是动量因子，用于调整上一步动量对参数更新时的重要程度，利用动量的方式可以使得算法跳出局部最优解的陷阱

梯度下降：

import matplotlib.pyplot as plt
import numpy as np

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

m = len(x_data)
w = 1.0

def forward(x, w):
    return w * x

def cost_fun(x, y, w):
    cost = 0
    for x_val, y_val in zip(x, y):
        pred = forward(x_val, w)
        cost += 1 / m * (pred - y_val) ** 2
    return cost

def gradient_fun(x, y, w):
    gradient = 0
    for x_val, y_val in zip(x, y):
        pred = forward(x_val, w)
        gradient += 2 * (1 / m) * x_val * (pred - y_val)
    return gradient

print('predict before training:', 4, forward(4, w))
epoches = 20
lr = 0.03
cost_list = []
for epoch in range(epoches):
    cost_val = cost_fun(x_data, y_data, w)
    grad_val = gradient_fun(x_data, y_data, w)
    w -= lr * grad_val
    cost_list.append(cost_val)
    print('epoch:', epoch, 'w:', w, 'cost:', cost_val)

print('predict after training:', 4, forward(4, w))


# 绘图
epoch = np.arange(epoches)
plt.plot(epoch, cost_list)
plt.xlabel('epoch')
plt.ylabel('cost')
plt.show()

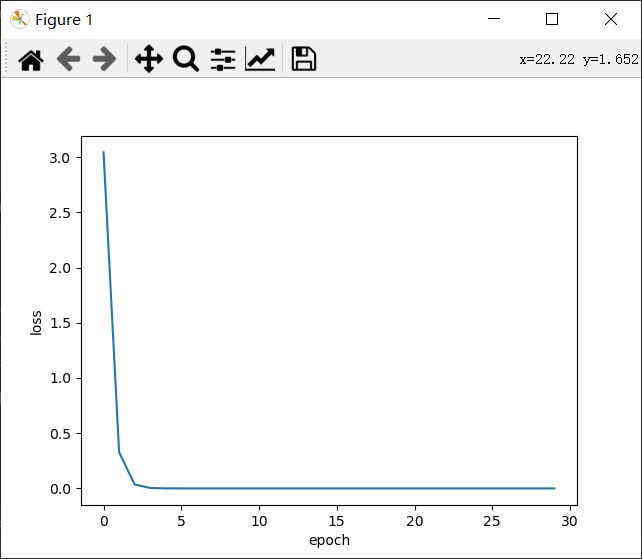
随机梯度下降：

import matplotlib.pyplot as plt
import numpy as np

x_data = [1.0, 2.0, 3.0]
y_data = [2.0, 4.0, 6.0]

w = 1.0
m = len(x_data)
def forward(x, w):
    return w * x

def loss_fun(x, y, w):
    pred = forward(x, w)
    loss = (pred - y) ** 2
    return loss

def gradient(x, y, w):
    pred = forward(x, w)
    grad = 2 * x * (pred - y)
    return grad

epoches = 30
lr = 0.03
loss_list = []

for epoch in np.arange(epoches):
    print('epoch:', epoch)
    loss_sum = 0
    for x_val, y_val in zip(x_data, y_data):
        grad = gradient(x_val, y_val, w)
        loss_val = loss_fun(x_val, y_val, w)
        loss_sum += loss_val
        w -= lr * grad
        print('\t', 'w:', w, 'loss:', loss_val)
    loss_list.append(loss_sum / m)
print('predict after training:', 4, forward(4, w))

epoch = np.arange(epoches)
plt.plot(epoch, loss_list)
plt.xlabel('epoch')
plt.ylabel('loss')
plt.show()

在学习率相同的情况下，采取随机梯度下降可以获得更快的收敛效果。

当数据集比较多的时候如果每次一个一个样本的计算会导致很大的计算量，训练时间会很长。如果每次使用一整个训练集花的时间少，但是收敛慢。

在实际训练中，一般采取折中的办法，对一个训练集划分批次。一个批次中可以包含多个样本。每次训练一个批次的数据，用一个批次的数据计算

损失并对参数进行更新。