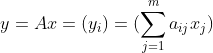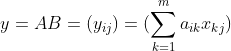tensorflow中的乘法
在tensorflow中向量、矩阵乘法大概可以分为两种:1、代数乘法;2、对应元素相乘
这两种运算使用两种运算模式:代数乘法使用matmul。对应元素相乘使用*号。下面给出例子。
一、代数乘法(使用函数matmul)
代数乘法就是高等代数(线性代数)中行列对应元素相乘再求和。
1、两个向量间相乘。w是1xn的行向量,x是nx1的列向量,相乘的结果是一个1x1的向量。
import tensorflow as tf
w =tf.random.normal([1, 6], mean=-1, stddev=4)
x =tf.random.normal([6,1])
print(w,x)
print(tf.matmul(w,x))2、一个矩阵乘以一个向量。A是一个nxm的矩阵,x是一个mx1的列向量,相乘的结果是一个nx1的列向量。
其中每个元素
w =tf.random.normal([5, 6], mean=-1, stddev=4)
x =tf.random.normal([6,1])
print(w,x)
print(tf.matmul(w,x))3、两个矩阵相相乘。A是一个nxm的矩阵,B是一个mxk的矩阵,相乘的结果是一个nxk的矩阵。
w =tf.random.normal([5, 6], mean=-1, stddev=4)
x =tf.random.normal([6,4])
print(w,x)
print(tf.matmul(w,x))总之,如果把向量(1xm)看成矩阵(nxm)的特例,也可以认为只有一种运算。
二、对应元素相乘(使用*号)
1、两个向量间。两个相同维数向量相乘,结果是一个向量。
![]()
w =tf.random.normal([6, 1], mean=-1, stddev=4)
x =tf.random.normal([6,1])
print(w,x)
print(w*x)2、一个矩阵乘以一个向量。结果是一个矩阵。
![]()
w =tf.random.normal([6, 5], mean=-1, stddev=4)
x =tf.random.normal([6,1])
print(w,x)
print(w*x)3、两个矩阵相乘。结果是一个矩阵。
![]()
w =tf.random.normal([6,5], mean=-1, stddev=4)
x =tf.random.normal([6,5])
print(w,x)
print(w*x)
三、注意事项:
1、代数乘法,第一个矩阵的列数与第二个矩阵的行数必须相同。代数运算的要求。
2、对应元素相乘,向量与向量间,矩阵与矩阵间,行、列数必须都相同。矩阵与向量间行数必须相同。