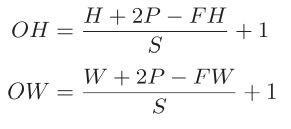深度学习入门-卷积神将网络(CNN)

深度学习入门-卷积神将网络(CNN)

整体结构

​ CNN与之前的神将网络不同的是，CNN中新出现了卷积层（Convolution层）和池化层（Pooling层）。

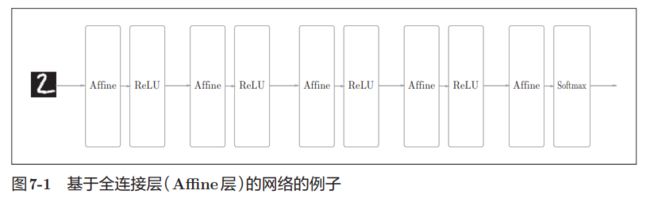
​ 之前介绍的神经网络中，相邻层的所有神经元之间都有连接，这称为全 连接（fully-connected）。另外，我们用Affine层实现了全连接层。如下图所示。

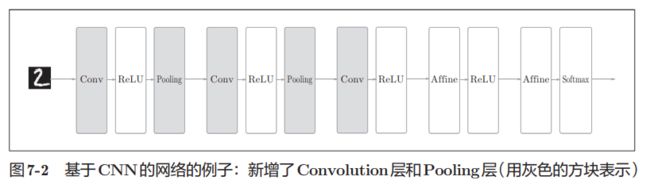
​ CNN的结构如下：

​ CNN 中新增了 Convolution 层 和 Pooling 层。CNN 的 层的连接顺序是“Convolution - ReLU -（Pooling）”（Pooling层有时会被省 略）。这可以理解为之前的“Affine - ReLU”连接被替换成了“Convolution - ReLU -（Pooling）”连接。靠近输出的层中使用了之前 的“Affine - ReLU”组合。此外，最后的输出层中使用了之前的“Affine - Softmax”组合。这些都是一般的CNN中比较常见的结构。

卷积层

全连接层存在的问题

​ 全连接层最大的问题就是：数据的形状被忽视了。。比如，输 入数据是图像时，图像通常是高、长、通道方向上的3维形状。但是，向全 连接层输入时，需要将3维数据拉平为1维数据。图像是3维形状，这个形状中应该含有重要的空间信息。因为全连接层会忽视形状，将全部的输入数据作为相同的神经元 （同一维度的神经元）处理，所以无法利用与形状相关的信息。

​ 而卷积层可以保持形状不变。当输入数据是图像时，卷积层会以3维 数据的形式接收输入数据，并同样以3维数据的形式输出至下一层。因此， 在CNN中，可以（有可能）正确理解图像等具有形状的数据。

卷积运算

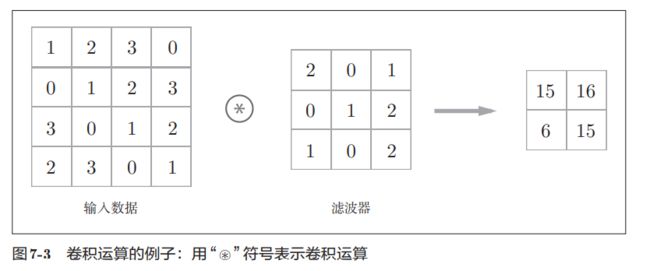
​ 我们首先来看一个例子：

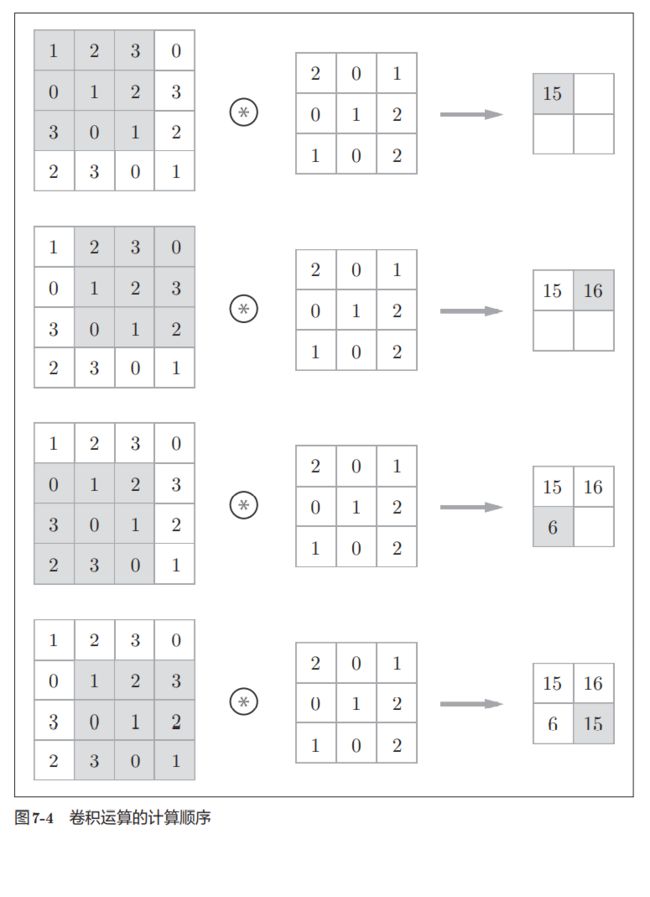
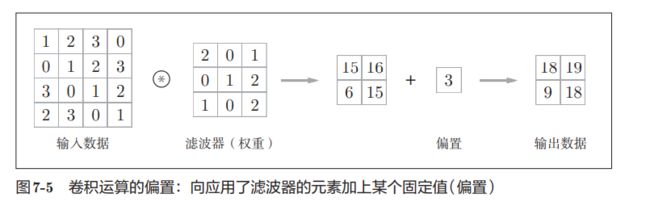
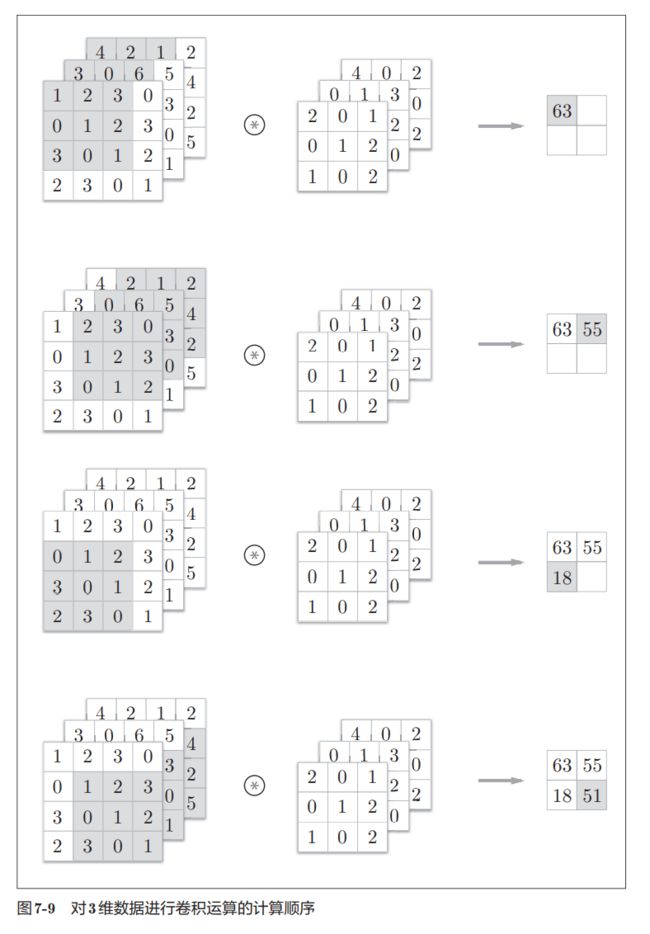
​ 在具体的运算实现上：

​ 每次运算将滤波器与阴影部分对应位置相乘再相加，即得到了输出结果。

​ 得到结果后，还需要去加上一个偏置，如下：

填充

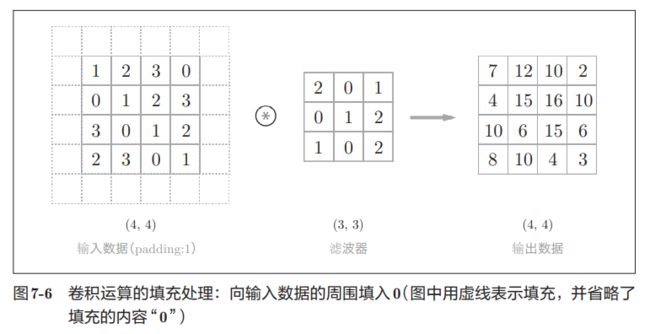
​ 填充是指，在进行卷积层的处理之前，有时要向输入数据的周围填入固定的数据（比 如0等）。再下面的例子中，对大小为(4, 4)的输入数据应用了幅度为1的填充。“幅 度为1的填充”是指用幅度为1像素的0填充周围。

​ 填充的目的主要是为了调整输出的大小。比如，对大小为(4, 4)的输入 数据应用(3, 3)的滤波器时，输出大小变为(2, 2)，相当于输出大小 比输入大小缩小了 2个元素。在进行若干次卷积之后，在某个时刻输出大小就有可能变为 1，导致无法再应用 卷积运算。为了避免出现这样的情况，就要使用填充。因此，填充的目的是为了使卷积运算就可以在保持空间大小不变 的情况下将数据传给下一层。

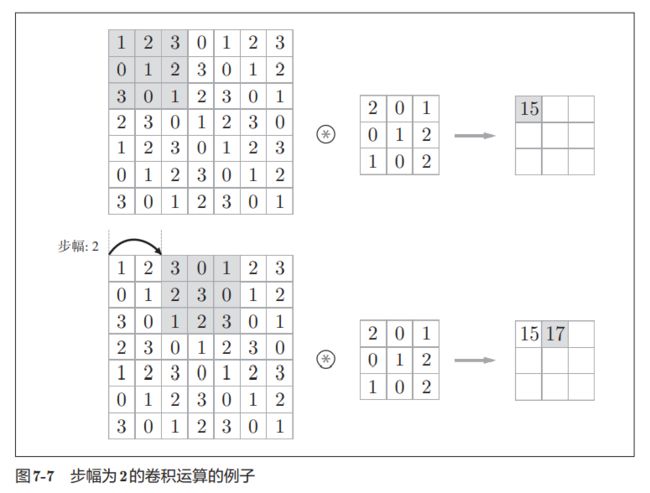
步幅

​ 步幅是指滤波器一次移动的步子的大小。

​ 综上，增大步幅后，输出大小会变小。而增大填充后，输出大小会变大。 如果将这样的关系写成算式，会如何呢？接下来，我们看一下对于填充和步 幅，如何计算输出大小。 这里，假设输入大小为(H, W)，滤波器大小为(FH, FW)，输出大小为 (OH, OW)，填充为P，步幅为S。此时，输出大小可通过下式进行计算。

3维数据的卷积运算

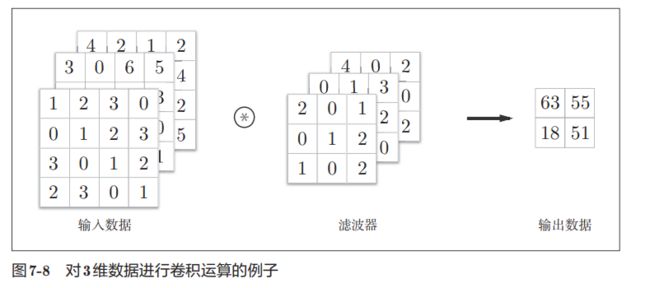
​ 对于3维数据的卷积运算，除了高长方向以外，还因该处理通道方向。

​ 对于三维数据的卷积，因为通道方向上有多个特征图，也有多个与之对应的滤波器。将相应位置上的特征图与滤波器做卷积运算，然后将多层得到的结果加在一起，即可得到最后的的结果。然后根据步幅移动滤波器，去做下一步的运算。

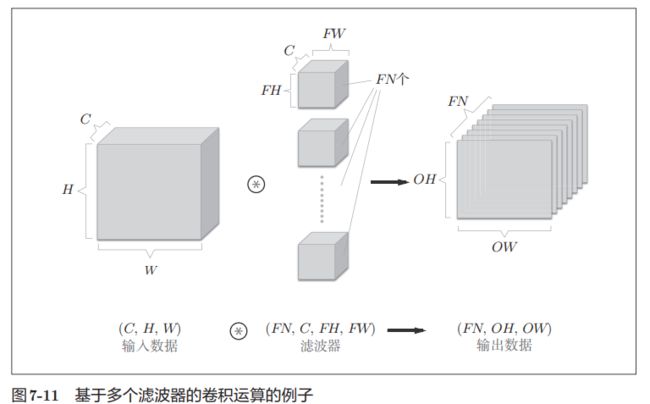
​ 上面的输出是通道数为1的特征图。那么，如果要在通道方向上也拥有多个卷积运算的输出，就需要用到多个滤波器（权重）。可以用下图表示：

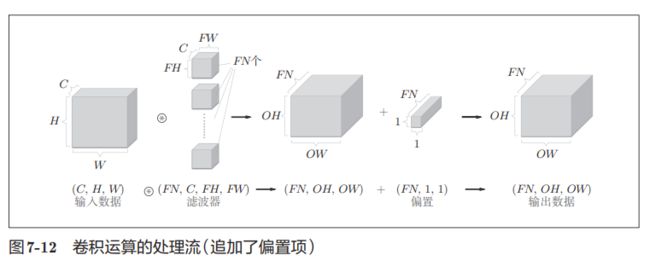
​ 如果考虑到偏置的问题，每一个通道只有一个偏置，如下图：

批处理

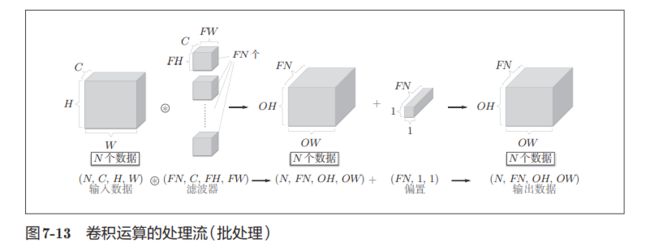
​ 为了一次性的处理一批次的数据，我们将将在各层间传递的数 据保存为4维数据。具体地讲，就是按(batch_num, channel, height, width) 的顺序保存数据。将图7-12中的处理改成对N个数据进行批处理时， 数据的形状如图7-13所示。

​ 这里需要注意的是，网络间传 递的是4维数据，对这N个数据进行了卷积运算。也就是说，批处理将N次 的处理汇总成了1次进行。

池化层

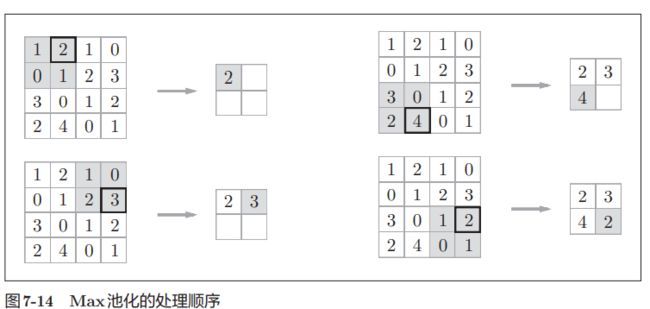
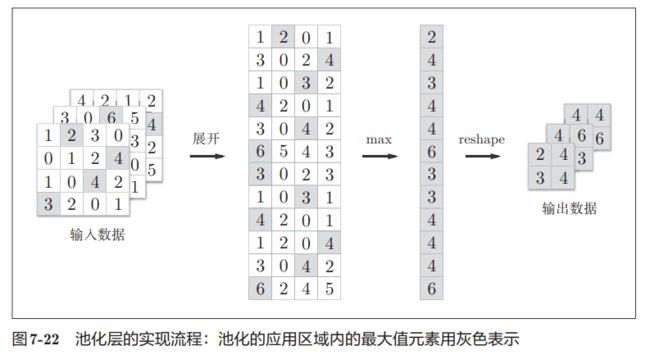
​ 池化是缩小高、长方向上的空间的运算。比如，如图所示，进行将 2 × 2的区域集约成1个元素的处理，缩小空间大小。

​ 上述例子是按步幅2进行2*2的MAX池化时的处理顺序。另外，一般来说，池化的窗口大小会和步幅设定成相同的值。

池化层具有的特征

​ 没有要学习的参数

​ 池化层和卷积层不同，没有要学习的参数。池化只是从目标区域中取最 大值（或者平均值），所以不存在要学习的参数。

​ 通道数不发生变化

​ 经过池化运算，输入数据和输出数据的通道数不会发生变化。计算是按通道独立进行的。

​ 对微小的位置变化具有鲁棒性（健壮）

​ 输入数据发生微小偏差时，池化仍会返回相同的结果。因此，池化对 输入数据的微小偏差具有鲁棒性。当输入的数据有微小的差错时，池化会吸收输入数据的偏差（根据数据的不同，结果有可 能不一致）。

池化层和卷积层的实现

4维数组

​ 如前所述，CNN中各层传播的数据是4维数据。比如数据的形状是(10, 1, 28, 28)，则它对应10个高为28、长为28、通道为1的数据。

x = np.random.rand(10,1,28,28)  #随机生成形如（10，1，28，28）的数据
print(x.shape)  #（10，1，28，28）

# 如果要访问第1个数据，只要写x[0]就可以了
print(x[0].shape) 

#如果要访问第1个数据的第1个通道的空间数据，可以写成下面这样。
print(x[0,0])

基于im2col的展开

​ 如果使用多层for循环语句去实现卷积运算，这样实现起来不仅麻烦，还存在处理过慢的缺点。所以，在这里，我们不使用for语句，而是使 用im2col这个便利的函数进行简单的实现。

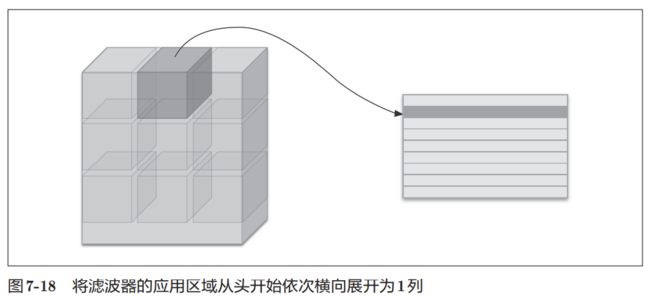
​ im2col是一个函数，将输入数据展开以适合滤波器（权重）。具体地说， 对于输入数据，将应用滤波器的区域（3维方块）横向展开为1列。im2col会 在所有应用滤波器的地方进行这个展开处理。

​ 为了便于观察，将步幅设置得很大，以使滤波器的应用区 域不重叠。而在实际的卷积运算中，滤波器的应用区域几乎都是重叠的。在滤波器的应用区域重叠的情况下，使用im2col展开后，展开后的元素个数会 多于原方块的元素个数。因此，使用im2col的实现存在比普通的实现消耗更 多内存的缺点。但是，汇总成一个大的矩阵进行计算，对计算机的计算颇有 益处。比如，在矩阵计算的库（线性代数库）等中，矩阵计算的实现已被高度最优化，可以高速地进行大矩阵的乘法运算。因此，通过归结到矩阵计算上，可以有效地利用线性代数库。

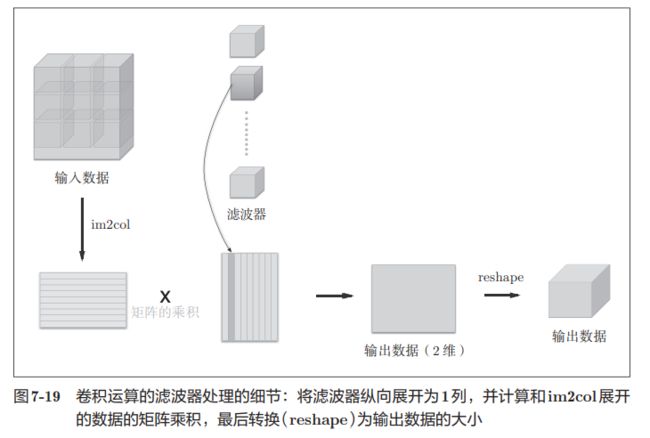
​ 使用im2col展开输入数据后，之后就只需将卷积层的滤波器（权重）纵向展开为1列，并计算2个矩阵的乘积即可

​ 基于im2col方式的输出结果是2维矩阵。因为CNN中 数据会保存为4维数组，所以要将2维输出数据转换为合适的形状。

卷积层的实现

​ im2col这一便捷函数具有以下接口。(该函数只负责把输入数据展开为2维矩阵)

​ 例子：

import sys, os
sys.path.append(os.pardir)
from common.util import im2col

x1 = np.random.rand(1, 3, 7, 7)
col1 = im2col(x1, 5, 5, stride=1, pad=0)
print(col1.shape) # (9, 75)

x2 = np.random.rand(10, 3, 7, 7) # 10个数据
col2 = im2col(x2, 5, 5, stride=1, pad=0)
print(col2.shape) # (90, 75)

​ 这里举了两个例子。第一个是批大小为1、通道为3的7 × 7的数据，第 二个的批大小为10，数据形状和第一个相同。分别对其应用im2col函数，在 这两种情形下，第2维的元素个数均为75。这是滤波器（通道为3、大小为 5 × 5）的元素个数的总和。批大小为1时，im2col的结果是(9, 75)。而第2 个例子中批大小为10，所以保存了10倍的数据，即(90, 75)。

​ im2col来实现卷积层：

class Convilution:
    def __init__(self, W, b, stride=1, pad=0):
        self.W = W
        self.b = b
        self.stride = stride
        self.pad = pad
    
    def forward(self, x):
        FN, C, FH, FW = self.W.shape
        N, C, H, W = x.shape
        out_h = int(1 + (H + 2*self.pad - FH) / self.stride)
        out_w = int(1 + (W + 2*self.pad - FW) / self.stride)
        
        col = im2col(x,FH,FW,self.stride,self.pad)
        col_W = self.W.reshape(FN,-1).T #将滤波器展开
        out = np.dot(col,col_W) + self.b
        
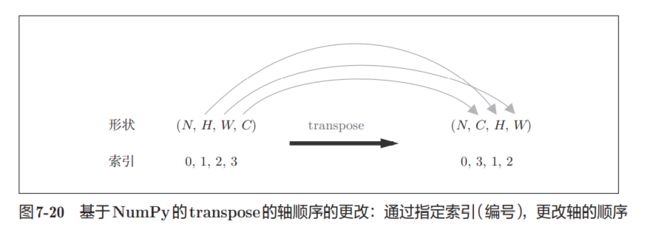
        #transpose(0, 3, 1, 2)的作用是将通道数放在高和宽的前面
        out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)
        return out

​ forward的实现中，最后会将输出大小转换为合适的形状。转换时使用了 NumPy的transpose函数。transpose会更改多维数组的轴的顺序。如图7-20 所示，通过指定从0开始的索引（编号）序列，就可以更改轴的顺序。

池化层的实现

​ 池化层的实现和卷积层相同，都使用im2col展开输入数据。不过，池化 的情况下，在通道方向上是独立的，这一点和卷积层不同。

​ 池化层的实现：

class Polling:
    def __init__(self, pool_h, pool_w, stride=1, pad=0):
        self.pool_h = pool_h
        self.pool_w = pool_w
        self.stride = stride
        self,pad = pad
def forward(self, x):
    N, C, H, W = x.shape
    out_h = int(1 + (H - self.pool_h) / self.stride)
    out_w = int(1 + (W - self.pool_w) / self.stride)
    
    # 展开
    col = im2col(x, self.pool_h, self.pool_w, self.stride, self.pad)
    col = col.reshape(-1, self.pool_h*self.pool_w) #这一步才算是展开到上面16*4的矩阵
    
    # 最大值
    out = np.max(col, axis=1)
    out = out.reshape(N, out_h, out_w, C).transpose(0, 3, 1, 2)
    
    return out

CNN的实现

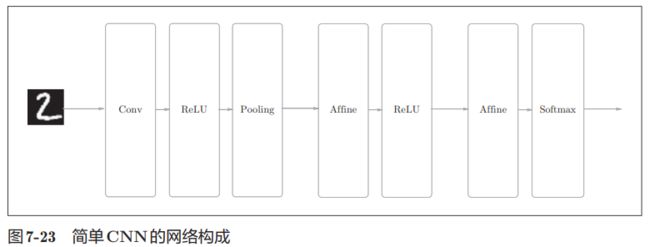
​ 我们已经实现了卷积层和池化层，现在来组合这些层，搭建进行手写数 字识别的CNN。如下图：

​ 网络的构成是“Convolution - ReLU - Pooling -Affine - ReLU - Affine - Softmax”，我们将它实现为名为SimpleConvNet的类。

​ SimpleConvNet的初始化（init），取下面这些参数：

​ SimpleConvNet类的实现：

class SimpleConvNet:
    def __init__(self,input_dim=(1,28,28),conv_param={'filter_num':30, 'filter_size':5,'pad':0, 'stride':1},hidden_size=100, output_size=10, weight_init_std=0.01):
        filter_num = conv_param['filter_num']
        filter_size = conv_param['filter_size']
        filter_pad = conv_param['pad']
        filter_stride = conv_param['stride']
        input_size = input_dim[1]
        conv_output_size = (input_size - filter_size + 2*filter_pad) / filter_stride + 1
        pool_output_size = int(filter_num * (conv_output_size/2) * (conv_output_size/2))
        
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(filter_num, input_dim[0],filter_size, filter_size)
        self.params['b1'] = np.zeros(filter_num)
        self.params['W2'] = weight_init_std * np.random.randn(pool_output_size,hidden_size)
        self.params['b2'] = np.zeros(hidden_size)
        self.params['W3'] = weight_init_std * np.random.randn(hidden_size, output_size)
        self.params['b3'] = np.zeros(output_size)
        
        self.layers = OrderedDict()
        self.layers['Conv1'] = Convolution(self.params['W1'],self.params['b1'],conv_param['stride'],conv_param['pad'])
        self.layers['Relu1'] = Relu()
        self.layers['Pool1'] = Pooling(pool_h=2, pool_w=2, stride=2)
        self.layers['Affine1'] = Affine(self.params['W2'],self.params['b2'])
        self.layers['Relu2'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W3'],self.params['b3'])
        
        self.last_layer = softmaxwithloss()
        
    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)
        return x
    
    def loss(self, x, t):
        y = self.predict(x)
        return self.lastLayer.forward(y, t)
    
    def gradient(self, x, t):
        # forward
        self.loss(x, t)
        
        # backward
        dout = 1
        dout = self.lastLayer.backward(dout)
        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)
        
        # 设定
        grads = {}
        grads['W1'] = self.layers['Conv1'].dW
        grads['b1'] = self.layers['Conv1'].db
        grads['W2'] = self.layers['Affine1'].dW
        grads['b2'] = self.layers['Affine1'].db
        grads['W3'] = self.layers['Affine2'].dW
        grads['b3'] = self.layers['Affine2'].db

小结