2020-NeurIPS-Path Integral Based Convolution and Pooling for Graph Neural Networks
2020-NeurIPS-Path Integral Based Convolution and Pooling for Graph Neural Networks

Paper: https://arxiv.org/abs/2006.16811
Code:
基于路径积分的图神经网络卷积与池化
图神经网络将传统神经网络的功能扩展到图结构数据。与CNNs类似,图卷积和池化的优化设计是成功的关键。作者借鉴物理学的思想,提出了一种基于路径积分的图神经网络(PAN),用于图上的分类和回归任务。具体来说,并考虑了一个卷积操作,它涉及到每个连接消息发送者和接收者的路径,其权重取决于路径长度,这对应于最大熵随机游走。它将图拉普拉斯变换推广到一个新的转移矩阵,称之为最大熵转移(MET)矩阵,它是由路径积分形式导出的。重要的是,MET矩阵的对角线条目与子图的中心性直接相关,从而导致一种自然和自适应的池化机制。PAN提供了一个通用的框架,可以针对不同大小和结构的图形数据进行定制。可以将大多数现有的GNN架构视为PAN的特殊情况。实验结果表明,PAN在各种图分类/回归任务中都取得了一流的性能。
模型
基于路径积分的图卷积
路径积分和 MET 矩阵 费曼路径积分公式将概率幅值 φ ( x , t ) φ(x,t) φ(x,t)解释为构型空间中的加权平均值,其中 φ 0 ( x ) φ_0(x) φ0(x)的贡献是通过将连接自身和 φ ( x , t ) φ(x,t) φ(x,t)的所有路径的影响(用 e i S [ x , x ] e^{iS[x, x]} eiS[x,x]表示)相加来计算的。这个公式后来被广泛应用于统计力学和随机过程中。这个公式本质上是通过考虑连续空间中所有可能路径的贡献来构造一个卷积。因此,作者提出一个统计力学模型,说明给定图上的不同节点之间如何共享信息。

在最一般的形式中,将具有 N N N个节点的图的第i个节点上的可观察对象 φ i φ_i φi写为

其中 Z i Z_i Zi是归一化因子,称为第 i i i个节点的配分函数。路径 l l l是一个连接节点的序列 ( l 0 l 1 . . . l ∣ l ∣ ) (l_0l_1...l_{|l|}) (l0l1...l∣l∣),其中 A l i l i + 1 = 1 A_{l_il_{i +1}} = 1 Alili+1=1,路径长度用 ∣ l ∣ |l| ∣l∣表示。
通过首先对路径长度进行调整,引入第 n n n层权重 k ( n ; I ) k(n;I) k(n;I)对于节点 I I I :

其中, g ( i , j ; n ) g (i, j;n) g(i,j;n)表示节点i和j之间长度为 n n n的路径数,或者能级 E ( n ) E(n) E(n)相对于节点i和j的状态密度,并且对图中的所有节点求和。能量 E ( n ) E(n) E(n)是 n n n的递增函数,这导致权重随着 n n n的增加而衰减通过应用最大路径长度 L L L的cutoff,交换(1)中的求和顺序以获得

配分函数可以显式写成
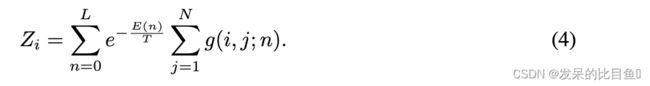
这种形式的一个很好的性质是可以很容易地计算出 g ( i , j ; n ) g(i,j;n) g(i,j;n)通过将邻接矩阵A的幂提升到 n n n,这是图论中邻接矩阵的一个众所周知的性质,即 g ( i , j ; n ) = A i j n g(i,j;n) = A^n_{ij} g(i,j;n)=Aijn。由转换矩阵M(量子力学中传播子的对应物)控制的自洽方程,它可以写成以下紧凑形式

其中 d i a g ( Z ) i = Z i diag(Z)_i = Z_i diag(Z)i=Zi。称矩阵为M最大熵跃迁(MET)矩阵,因为它在微正则系综下实现了最大熵。这个转换矩阵取代了拉普拉斯图的角色。
更一般地,可以将考虑的路径限制为,例如,最短路径或自避免路径。 g ( i , j ; n ) g (i, j;n) g(i,j;n)将采用更复杂的形式,矩阵 A n A^n An需要进行相应的修改。
PAN convolution 这个特征态,或者说这个体系 { ψ i } \{\psi_i\} {ψi}满足 M ψ i = λ i ψ i Mψ_i = λ_iψ_i Mψi=λiψi。类似于由图拉普拉斯构成的基,可以根据MET矩阵的谱来定义图卷积,它现在有了独特的物理意义。然而,在每次迭代中对M进行对角化在计算上是不切实际的。为了降低计算复杂度,应用了类似于GCN技巧,直接将 M M M乘以输入的左侧,并在右侧伴随另一个权重矩阵 W W W。然后卷积层被简化为一个简单的形式

其中 h h h为层数。对输入 X X X应用 M M M本质上是给定节点的邻居之间的加权平均,这导致了一个问题,即与路径积分公式一致的归一化是否在数据驱动的上下文中工作得最好。由于对于无向图,连接节点之间的确切相互作用是未知的,作为折衷,对称归一化可以优于两个极端,即使它可能不是最优的。这种考虑将引向最后的完善步骤,即将M中的规范化 z − 1 z^{-1} z−1更改为对称规范化版本。卷积层就变成了
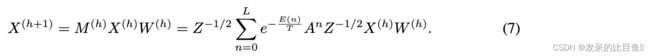
基于路径积分的图池化
对于图分类和回归任务,另一个关键组件是池化机制,能够处理具有可变大小和结构的图输入。这表明PAN框架提供了基于MET矩阵的节点重要性的自然排名,与子图中心性密切相关。这种池化方案称为PANPool,除了卷积外不需要做其他工作,可以自适应地发现底层的局部原子构型。
MET矩阵和子图中心性 在复杂网络社区中已经提出了许多不同的方法来对图中节点的重要性进行排名。最直接的是度中心性(DC),它计算邻居的数量,其他更复杂的度量包括,例如,中间中心性(BC)和特征向量中心性(EC)。尽管这些方法确实给出了节点的全局重要性的具体度量,但它们通常无法捕获局部模式。
Hybrid PANPool. 为了结合局部主题的贡献和全局重要性,作者提出了一种使用简单线性模型的混合PAN池(用PANPool表示)。全局重要性可以用但不限于输入信号X本身的强度来表示。通过一个可训练的参数向量 p ∈ R d p \in R^d p∈Rd投影特征 X ∈ R N × d X \in R^{N \times d} X∈RN×d,并将其与MET矩阵的对角线diag(M)相结合,以获得一个分数向量
![]()
在这里,β是一个真正的可学习参数,它控制着对这两个潜在竞争因素的重视。然后,PANPool从该分数排序的节点中选取一部分,输出池化后的特征数组 X ~ ∈ R K × d \tilde{X} \in R^{K \times d} X~∈RK×d和对应的邻接矩阵 A ~ ∈ R K × K \tilde{A} \in R^{K \times K} A~∈RK×K。公式(8)中的新节点评分联合考虑了节点特征(全局级别)和图结构(局部级别)。在图2中,PANPool倾向于选择在本地和全局都很重要的节点。
实验
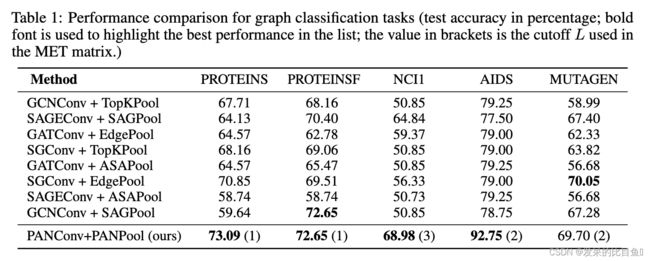
表1报告了几种GNN模型的分类测试精度。PAN在所有数据集上都具有出色的性能,并且在五个数据集中的四个数据集上实现了最高的精度,并且在某些情况下,将技术水平提高了几个百分点。即使是MUTAGEN, PAN的性能也排在第二。最有趣的是,对于不同类型的图数据,MET矩阵的最高阶L的最佳选择是不同的。它证实了PAN的灵活性使其能够学习和适应给定图形数据的最自然表示。

图3表明。HD的体积分数(被粒子覆盖的)φHD固定在0.5,而我们调优 φ R S A φ_{RSA} φRSA来控制RSA与其他两个分布的相似性(泊松点模式对应于 φ R S A = 0 φ_{RSA}=0 φRSA=0)。随着 φ R S A φ_{RSA} φRSA越来越接近0.5,RSA模式越来越难以与HD模式区分。

图4中比较了PANConv+PANPool与GCNConv+TopKPool训练中的验证损失和准确率趋势。结果表明,PAN模型的学习和泛化能力优于GCN和GIN模型。
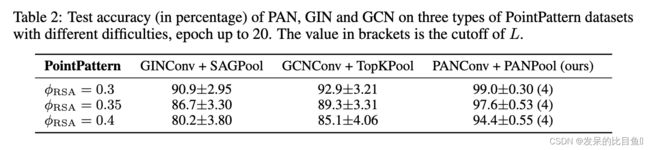
表2显示了三个网络在三个PointPattern数据集上的测试精度的平均值和标准差。PAN在所有数据集上都优于GIN和GCN模型,精度提高了5%至10%,同时显著降低了方差。