论文笔记 -- Learning Representations for Time Series Clustering

Learning Representations for Time Series Clustering

原文： Learning Representations for Time Series Clustering (neurips.cc)

出处： NeurIPS-2019 （Neural Information Processing Systems）

摘要： 在类别信息不可用的情况下，时间序列聚类是一种基本的无监督技术。它已广泛应用于基因组数据，异常检测，以及模式识别等重要的领域。虽然基于特征的时间序列聚类方法对噪声和异常值具有鲁棒性，并且可以降低数据的维数，但它们通常依赖于领域知识来手动构建高质量的特征。seq2seq模型可以通过设计适当的学习目标，如重建和上下文预测，以无监督的方式从序列数据中学习表示。当将seq2seq应用于时间序列聚类时，获得一个有效表示序列时间动态、多尺度特征和良好聚类特性的表示仍然是一个挑战。如何最好地提高编码器的能力仍然是一个悬而未解决的问题。在本文中，我们提出了一种新的无监督时间表示学习模型，即深度时间聚类表示(DTCR)，它将时间重建和k-means目标集成到seq2seq模型中。这种方法改进了聚类结构，从而获得了特定于聚类的时间表示。此外，为了提高编码器的能力，我们提出了一种假样本生成策略和辅助分类任务。在大量的时间序列数据集上进行的实验表明，与现有的方法相比，DTCR是最先进的。可视化分析不仅显示了特定于聚类的表示的有效性，并且不会受k-means错误的影响，显示了学习过程的稳健性。

Motivation

1、基于特征的方法所选择的特征通常是线性的，但是非线性作用在时间序列中更为常见

2、如果使用下游分类任务对一般表示法进行微调，则可以显著提高其表示效果（与任务相关的表示的好处）

Contribution

1、提出了一种新的无监督的时间序列聚类时间表示学习模型，该模型集成了时间重构和K-means目标来生成特定于聚类的时间表示。

2、提出了一种时间序列的假样本生成策略，并引入了编码器的辅助分类任务，以提高其能力。

3、在大量的基准时间序列数据集上的实验结果表明，该模型取得了最先进的性能。可视化分析说明了聚类特定的时间表示的有效性，并证明了学习过程的稳健性。

Model

DTCR工作

1、DTCR将时间重建和k-means目标整合到seq2seq模型中。

2、DTCR将双向扩张递归神经网络作为编码器，使学习到的表示能够捕获时间序列的时间动态和多尺度特征。

3、DTCR学习到的表示在k-means目标的指导下形成了一个聚类结构。

4、DTCR为了进一步提高编码器的能力使用了一种时间序列的假样本生成策略，并引入了该编码器的辅助分类任务。

DTCR流程

输入

数据集$D$、类簇个数$K$、更新间隔$T$、最大迭代次数$MaxIter$

输出

使用K-means的聚类结果$s$

变量定义

时间序列：$D=\{x_1,x_2,\dots ,x_n\}$，其中$x_i$表示单个时间序列，为一个$T$维实值向量，$x_i=\{x_{i1},x_{i2},\dots ,x_{iT}\}$

编码器：$fenc:x_i\to h_i$ 双向多层扩张递归神经网络

解码器：$fdec:h_i\to x_i$ 单层递归神经网络

$h_i$：$m$维的时间序列潜在表示

算法流程

通过最小化整体损失来达到模型的优化效果，整体损失定义为：
$$L_{DTCR}=L_{reconstruction}+L_{classification}+L_{k-means}$$
其中:

$L_{reconstruction}$为使用表示学习将原数据重构为聚类的输入的损失 $seq2seq原来的损失$

$L_{classification}$为通过输入的假样本做分类任务的损失 $用于辅助编码器的学习过程$

$L_{k-means}$为将编码器编码过后的数据进行k-means聚类的损失 $用于判定所学习的特征是否适用于聚类$

reconstruction误差

该模型采用均

方误差来表示重构误差

定义：
$$L_{reconstruction}=\frac{1}{n}\sum _{i=1}^n||x_i-{\hat{x}}_i|{|}_2^2$$
解释：DTCR模型采用seq2seq模型进行编码和解码，采用均方误差对编码和解码前后的数据进行误差计算，在最小化损失时可以保证编码和解码前后的数据尽可能保持一致（即保留原始时间序列的更多特征）

k-means误差

作用：指导编码器的学习，使得学习到的表示方法更适用于聚类，解决重构后的数据特征并不一定适用于聚类的问题

定义流程：

给定一个静态矩阵$H\in {\mathbb{R}}^{m\times N}$，根据Spectral Relaxation for K-means Clustering 所诉的方法，最小化$L_{k-means}$可以转化成$H{H}^T$的迹最大化问题，这一问题可以找到全局最优解。即：
$$L_{k-means}=Tr(H^{T}H)-Tr(F^T{H}^{T}HF)$$
其中$F\in {\mathbb{R}}^{N\times k}$时聚类的指示矩阵，假设到$H$是给定的，通过将$F$设置为任意正交矩阵，上式可进一步转换成迹最大化问题，如下：

应该是将初始的指示矩阵设置为一个类别数等于样本数的矩阵
$$\underset{F}{\max }Tr(F^T{H}^{T}HF),s.t.F^{T}F=I$$
根据KyFan范数，$F$的解析解为组成$H$的前$K$个奇异向量。

在模型中，$H$是通过网络学习的，并不是静态的，$Tr(H^{T}H)$可以作为训练$H$过程的一个正则化项，所以可以将损失定义为下式：
$$\underset{H,F}{\min }J(H)+\frac{\lambda }{2}[Tr(H^{T}H)-TR(F^T{H}^{T}HF)],s.t.F^{T}F=I$$
其中，$J(H)$为$L_{reconstruction}$和$L_{classification}$之和，在DTCR的训练过程中由迭代更新$F$和$H$两个步骤组成。

参考Robust Spectral Learning for Unsupervised Feature Selection，$H$的更新策略为，固定$F$，使用标准梯度下降法（SGD）进行更新，梯度为：$\nabla J(H)+\lambda H(I-F{F}^T)$。

参考k-Shape: Efficient and Accurate Clustering of Time Series，$F$的更新策略为，固定$H$，通过计算$H$的$k$阶截断奇异值分解（SVD）方程的解析解来更新$F$。更新公式为${\max }_{F}Tr(F^T{H}^{T}HF),s.t.F^{T}F=I$。

classification误差

假样本生成策略：给定一个时间序列$x_i\in {\mathbb{R}}^T$，通过随即变换一些时间步长来生成他的假样本。所选时间序列的步长为$\lfloor \alpha ,T\rfloor$，其中$\alpha \in [0,1]$是一个超参数；时间步长为seq2seq模型中的一个概念。

辅助分类任务是训练编码器检测给定的时间序列是实的还是假的。形式上，编码器通过最小化以下损失函数进行训练：
$${\hat{y}}_i=W_{fc2}(W_{f}c1h_i)$$

$$L_{classification}=-\frac{1}{2N}\sum _{i=1}^{2N}\sum _{j=1}^{2}1\{y_{i,j}=1\}\log \frac{\exp {\hat{y}}_{i,j}}{{\sum }_{j=1}^2\exp ({\hat{y}}_{i,j})}$$

其中，$y_i$为one-hot向量，表示真假；${\hat{y}}_i$为预测结果的真假。为简单起见，忽略偏置项。$W_{fc1}\in {\mathbb{R}}^{m\times d}$$W_{fc2}\in {\mathbb{R}}^{d\times 2}$为全连接层的参数，d设置为128。

整体损失
$$L_{DTCR}=L_{reconstruction}+L_{classification}+\lambda L_{k-means}$$
其中，$\lambda$为正则化系数，重构损失为seq2seq模型编码和解码过程的损失，分类损失和k-means损失用于指导编码器的学习，通过真假样本的训练策略并利用分类损失可以最大化的保留原始时间序列的特征，引入k-means损失可以使得学习到的特征更适用于聚类。

Experiment

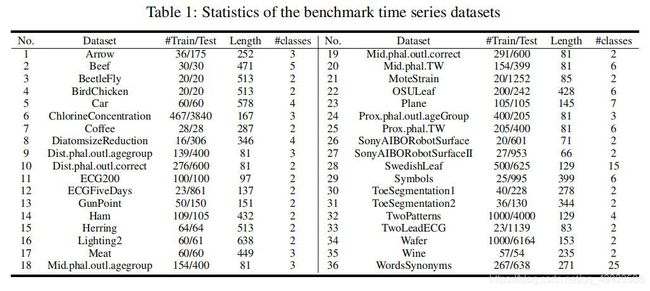
数据集：UCR中的36个数据集

训练过程：使用Salient subsequence learning for time series clustering中的方式，在训练集上进行训练。采用双向多层扩张递归神经网络作为编码器，捕获时间序列的动态多尺度特征。实验中，将网络层数和每层的扩张数设置为3，1和4，16，这样设置可以得出更好地训练结果。再通过分类损失和k-means损失进行调整训练；最后的解码器是一个单层的递归神经网络。解码器以编码器的最终隐藏状态作为初始状态，执行迭代预测，即$t-1$的输出作为$t$的输入。为了减少随机初始化的影响，对每个实验运行5次，并对平均值和标准差进行统计。

优化器：Adam优化器

初始学习率：0.005

评价指标：兰德指数、标准互信息 详情：聚类算法的性能度量方法

数据集介绍

使用UCR数据集中的36个数据集的情况

Baseline方法

k-means：在完整时间序列上使用k-means方法

UDFS：使用结构多样性探索、局部信息探索和特征相关性的无监督特征选择

NDFS：非负鉴别特征选择，采用正则化回归和非负光谱分析作为特征选择的联合框架

RUFS：利用鲁棒正交非负矩阵分解联合进行特征学习的鲁棒无监督特征学习

RSFS：无监督特征选择的鲁棒谱学习，将谱回归与稀疏图嵌入相结合

KSC：通过缩放距离度量并计算用于质心计算的矩阵的谱范数使用k-means进行聚类

k-DBA：通过DBA方法获得质心，采用k-means和DTW结合进行聚类

k-shape：一种可伸缩的迭代细化程序来探索具有标准化交相关度量的时间序列的形状

u-shapelet：一种时间序列聚类方法，忽略其余数据，只使用本地模式对时间序列进行聚类

DTC：以预测分布和目标分布之间的KL散度为指导，学习非线性特征

USSL：整合了形状学习、形状正则化、谱分析和伪标签的优势，以帮助更好地聚类未标记的时间序列

DEC：学习从数据空间到低维特征空间的映射，并在其中迭代优化聚类目标

IDEC：通过优化基于KL散度的聚类损失来控制特征空间映射数据，并维护原数据局部结构

对比试验

11种最近的有代表性的时间序列聚类方法（K-means, UDFS, NDFS, RUFS, RSFS, KSC, KDBA, k-shape, u-shapelet, DTC, USSL），两种时间序列深度聚类方法（DEC, IDEC）

差异的显著性判断：威尔科克森符号秩检验（观测值和零假设的中心位置之差的绝对值的秩分别按照不同的符号相加作为其检验统计量）

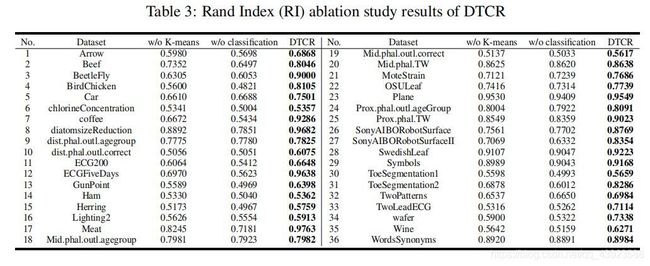
消融实验

为了验证$L_{classification} $和 $L_{k-means}$对模型的有效性，进行无k-means损失和无分类损失情况下的消融实验

各项损失的贡献

在两个数据集上对模型做消融实验，对比可以看出在两项损失的共同做一下聚类效果明显优于单独作用

学习表示的过程

在ECGFiveDays数据集上的学习过程

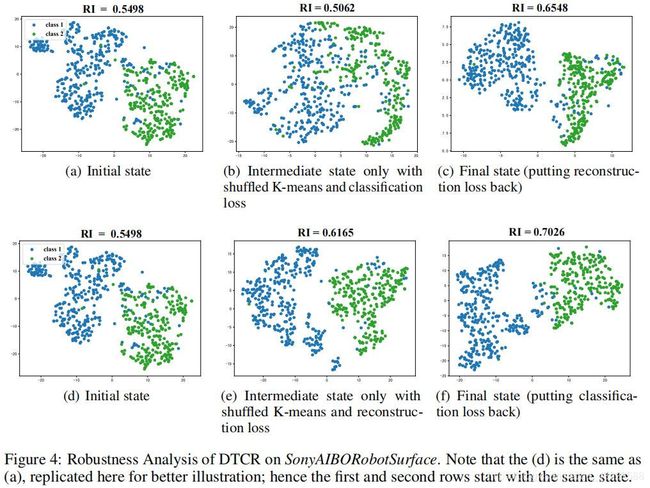
鲁棒性分析

原文模型引入了k-means损失，但是k-means在直到编码器学习过程中，并不能保证其结果的准确性，所以当k-means结构出错时对其指导的学习过程会有影响，但是DTCR模型可以在局部重建的帮助下进行错误纠正。

模型共有三个损失$L_{reconstruction}$、$L_{classification}$、$L_{k-means}$，假设$L_{k-means}$损失出错，需要探究$L_{reconstruction}$、$L_{classification}$在模型防止被错误的$L_{k-means}$误导方面由更重要的作用。

实验过程：

• 初始标识设置为使用50次迭代过程中的所有损失进行模型训练
• 之后随机打乱聚类的指示矩阵，进行50次迭代，此过程只保留$L_{reconstruction} $或$ L_{classification}$
• 最后将缺失的损失项加入，再次进行50次迭代并计算损失，得到最终状态

超参数分析

使用10个数据集进行超参数选择，固定其余超参数，每次调整一个超参数

需要调整的超参数$\lambda$，隐藏层的维度，扩张数（双向多层扩张RNN），$T$

主要方法参考文献

Spectral Relaxation for K-means Clustering

Robust Spectral Learning for Unsupervised Feature Selection

k-Shape: Efficient and Accurate Clustering of Time Series

Salient subsequence learning for time series clustering