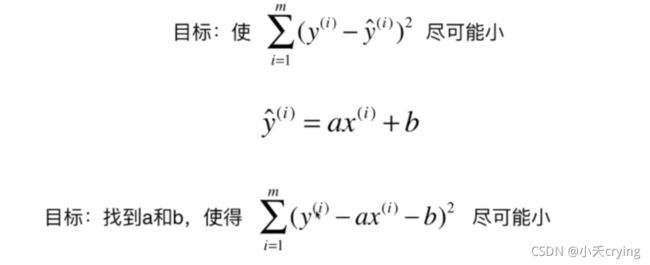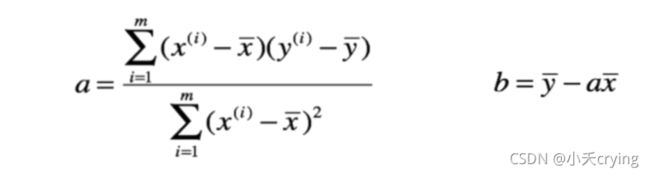机器学习基础学习-解析解实现简单线性回归

这里主要是因为博主作业要求，所以记录一下。关于一元线性回归问题的理论部分其实网上已经有很多解析了，这里记录一下简单的代码实现

大佬绕路

第一种解析解的方法

首先其实实现一元线性回归在我的理解就是，我们首先有许多的样本点，我们需要拟合出最接近这些样本点的一条直线，于是我们假定这条直线是y=ax+b,就是我们以前学过的一元函数。然后因为我们希望尽可能的拟合，所以需要求用每个点减去我们的最佳拟合线上的点的差值最小，可以进一步得到方差，在取得了方差后，要满足所有数据和我们最后的曲线基本吻合，那么就是求这个差值最小的情况，即求极小值点，为了求极小值，我们求导使其等于零，这样可以取得对应的a,b的值，而我们代码实现其实主要的部分也是求a、b的值

接下来上来代码

# 实现一维线性回归：解析解

import numpy as np
import matplotlib.pyplot as plt

# 这里只是简单定义了5个值
x = np.array([1., 2., 3., 4., 5.])
y = np.array([1., 3., 2., 3., 5.])

plt.scatter(x, y)
plt.show()

# x,y的均值
x_mean = np.mean(x)
y_mean = np.mean(y)

numerator = 0.0 # 分子
denominator = 0.0 # 分母

for x_i, y_i in zip(x, y):
  numerator += (x_i - x_mean) * (y_i - y_mean)
  denominator += (x_i - x_mean) ** 2

# 求解a
a = numerator / denominator
# 求解b
b = y_mean - a * x_mean

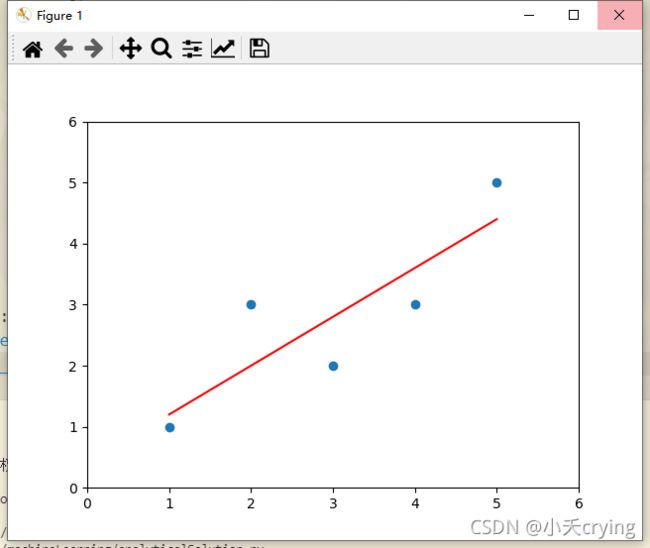
y_hat = a * x + b # 通过刚刚求解的a,b，基于每一个x所属的特征值进行预测

plt.scatter(x, y) # 通过散点图的方式把x，y绘制出来
plt.plot(x, y_hat, color = 'r') # 绘制直线(x采用刚刚同样的x值,y采用刚刚预测的y_hat)
plt.axis([0, 6, 0, 6]) # 规定坐标轴范围
plt.show()

运行结果
定义的五个值

预测结果

针对上课内容重新编写一套

其实和上面相似，在上面的方法中主要是求出a,b。这里是求出w和b。总体思想差别并不大


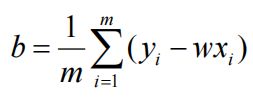
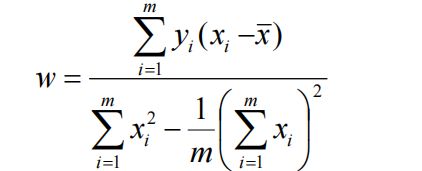
代码

# 实现一维线性回归：解析解(求w，b)

import numpy as np
import matplotlib.pyplot as plt

# 这里只是简单定义了5个值
x = np.array([1., 2., 3., 4., 5.])
y = np.array([1., 3., 2., 3., 5.])

plt.scatter(x, y)
plt.show()

# x,y的均值
x_mean = np.mean(x)
y_mean = np.mean(y)

numerator = 0.0 # w的分子
denominator_1 = 0.0 # w的分母的第一项
denominator_2 = 0.0 # w的分母的第二项(不包含1/m)
denominator = 0.0 # 分母

b_sum = 0.0
num = 0

for x_i, y_i in zip(x, y):
  numerator += y_i * (x_i - x_mean)
  denominator_1 += x_i ** 2
  denominator_2 += x_i
  num += 1

print(num)
# 求解w
denominator = denominator_1 - 1 / num * (denominator_2 ** 2)
w = numerator / denominator
# 求解b
for x_i, y_i in zip(x, y):
  b_sum += y_i - w * x_i
b = 1 / num * b_sum

y_hat = w * x + b # 通过刚刚求解的a,b，基于每一个x所属的特征值进行预测

plt.scatter(x, y) # 通过散点图的方式把x，y绘制出来
plt.plot(x, y_hat, color = 'r') # 绘制直线(x采用刚刚同样的x值,y采用刚刚预测的y_hat)
plt.axis([0, 6, 0, 6]) # 规定坐标轴范围
plt.show()

对结果来看，两种方法是一样的。

增加样本

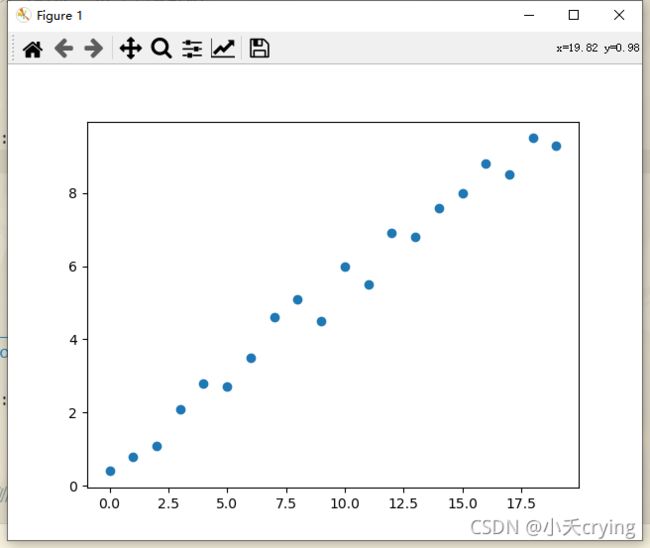
上面所述两种方法都是数据情况比较少的情况，由于博主刚刚接触机器学习，还没有引入任何数据集。现在只能手动增加样本

# x轴数据
x = np.arange(20)
# y轴数据
y = np.array([0.4, 0.8, 1.1, 2.1, 2.8, 2.7, 3.5, 4.6, 5.1, 4.5, 6.0, 5.5, 6.9, 6.8, 7.6, 8.0, 8.8, 8.5, 9.5, 9.3])

记得绘图时绘图数据范围也要更改

plt.axis([0, 18, 0, 9]) # 规定坐标轴范围

下面是总体代码（其实和上述的第二种方法相比，只是增加了数据，上一段代码和这一段只用看一段即可）

# 实现一维线性回归：解析解(求w，b)

import numpy as np
import matplotlib.pyplot as plt

# # 这里只是简单定义了5个值
# x = np.array([1., 2., 3., 4., 5.])
# y = np.array([1., 3., 2., 3., 5.])
# 增加数据量
# x轴数据
x = np.arange(20)
# y轴数据
y = np.array([0.4, 0.8, 1.1, 2.1, 2.8, 2.7, 3.5, 4.6, 5.1, 4.5, 6.0, 5.5, 6.9, 6.8, 7.6, 8.0, 8.8, 8.5, 9.5, 9.3])
plt.scatter(x, y)
plt.show()

# x,y的均值
x_mean = np.mean(x)
y_mean = np.mean(y)

numerator = 0.0 # w的分子
denominator_1 = 0.0 # w的分母的第一项
denominator_2 = 0.0 # w的分母的第二项(不包含1/m)
denominator = 0.0 # 分母

b_sum = 0.0
num = 0

for x_i, y_i in zip(x, y):
  numerator += y_i * (x_i - x_mean)
  denominator_1 += x_i ** 2
  denominator_2 += x_i
  num += 1

print(num)
# 求解w
denominator = denominator_1 - 1 / num * (denominator_2 ** 2)
w = numerator / denominator
# 求解b
for x_i, y_i in zip(x, y):
  b_sum += y_i - w * x_i
b = 1 / num * b_sum

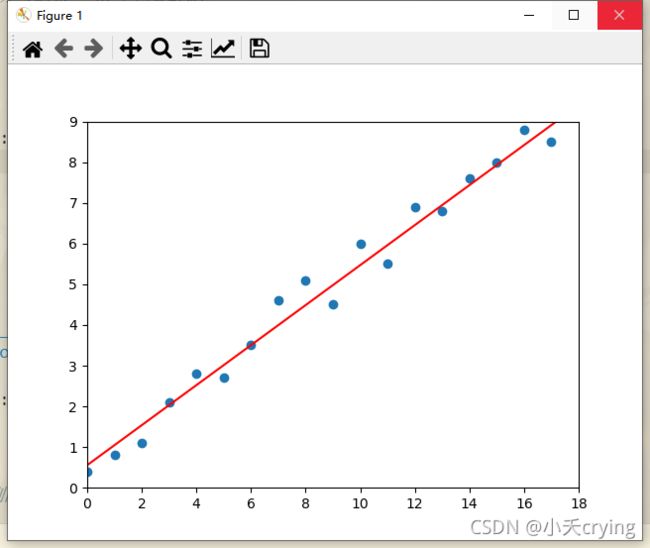
y_hat = w * x + b # 通过刚刚求解的w,b，基于每一个x所属的特征值进行预测

plt.scatter(x, y) # 通过散点图的方式把x，y绘制出来
plt.plot(x, y_hat, color = 'r') # 绘制直线(x采用刚刚同样的x值,y采用刚刚预测的y_hat)
plt.axis([0, 18, 0, 9]) # 规定坐标轴范围
plt.show()

下面是运行结果

随机数据集

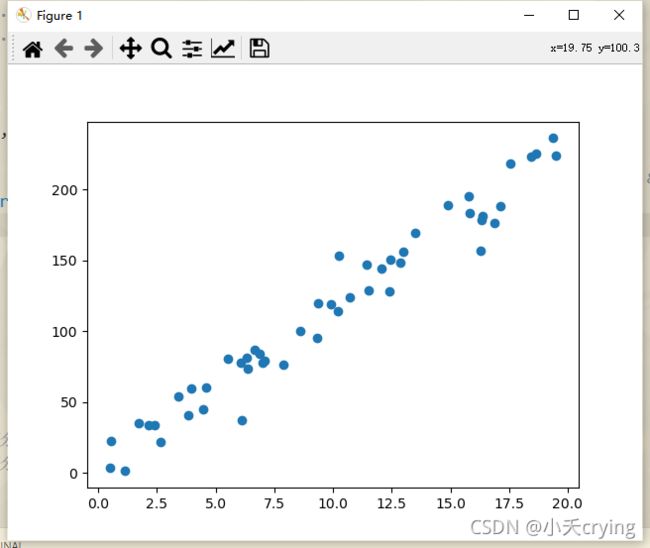
最后我们采用随机数据集

x = np.random.uniform(0.0, 20.0, size=50)
# y轴数据
y = x * 12 + np.random.normal(loc=0, scale=12.0, size=50)

总体代码

# 实现一维线性回归：解析解(求w，b)

import numpy as np
import matplotlib.pyplot as plt

# # 这里只是简单定义了5个值
# x = np.array([1., 2., 3., 4., 5.])
# y = np.array([1., 3., 2., 3., 5.])
# 增加数据量
# x轴数据
# x = np.arange(20)
x = np.random.uniform(0.0, 20.0, size=50)
# y轴数据
# y = np.array([0.4, 0.8, 1.1, 2.1, 2.8, 2.7, 3.5, 4.6, 5.1, 4.5, 6.0, 5.5, 6.9, 6.8, 7.6, 8.0, 8.8, 8.5, 9.5, 9.3])
y = x * 12 + np.random.normal(loc=0, scale=12.0, size=50)
print(y)
plt.scatter(x, y)
plt.show()

# x,y的均值
x_mean = np.mean(x)
y_mean = np.mean(y)

numerator = 0.0 # w的分子
denominator_1 = 0.0 # w的分母的第一项
denominator_2 = 0.0 # w的分母的第二项(不包含1/m)
denominator = 0.0 # 分母

b_sum = 0.0
num = 0

for x_i, y_i in zip(x, y):
  numerator += y_i * (x_i - x_mean)
  denominator_1 += x_i ** 2
  denominator_2 += x_i
  num += 1

print(num)
# 求解w
denominator = denominator_1 - 1 / num * (denominator_2 ** 2)
w = numerator / denominator
# 求解b
for x_i, y_i in zip(x, y):
  b_sum += y_i - w * x_i
b = 1 / num * b_sum

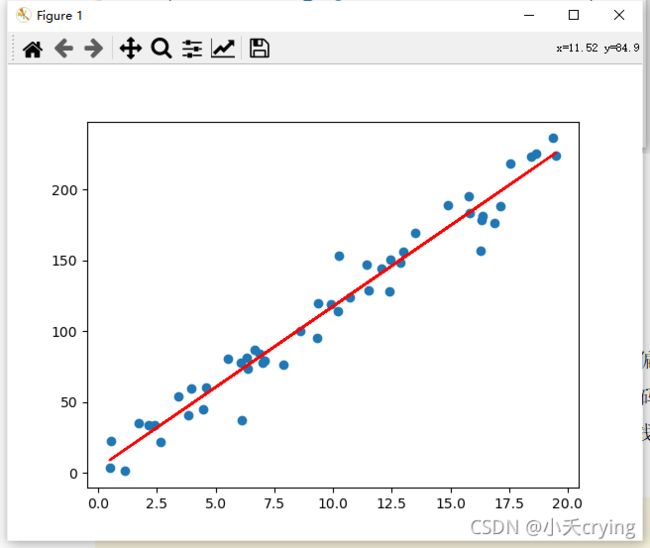
y_hat = w * x + b # 通过刚刚求解的w,b，基于每一个x所属的特征值进行预测

plt.scatter(x, y) # 通过散点图的方式把x，y绘制出来
plt.plot(x, y_hat, color = 'r') # 绘制直线(x采用刚刚同样的x值,y采用刚刚预测的y_hat)
# plt.axis([0, 25, 0, 210]) # 规定坐标轴范围
plt.show()

运行结果