基于K-Means聚类算法对NBA球员数据的聚类分析

  聚类分析的研究成果主要集中在基于距离（或者称为基于相似度）的聚类方法，用距离来作为相似性度量的优点是十分直观，从我们对物体的识别角度来分析，同类的数据样本是相互靠近的，不同类样本应该相聚较远。K-Means聚类算法是划分聚类方法中最常用、最流行的经典算法，许多其他的算法都是K-Means聚类算法的变种。其主要思想是通过迭代过程将数据集划分为不同类别，使评价聚类性能的准则函数达到最优，使生成的每个聚类类内紧凑，类间独立。
  本文介绍并实践了一种无监督的聚类算法——K-Means聚类，结合“簇内离差平方和拐点法”、“轮廓系数法”两种方法进行K值的选取。从虎扑上获取球员数据之后，使用K-Means算法对NBA球员数据集进行聚类，我们通过观察聚类的结果，把球员分成三种类别，可以对比球员的价值，在实际应用中可以作为参考，帮助球队进行人才的挑选。

1.数据获取

使用pandas中的read_html函数读取虎扑体育网页中的球员数据表，代码如下

import pandas as pd
import numpy as n

# 读取网页中的数据表
table = []
for i in range(1,7):
    table.append(pd.read_html('https://nba.hupu.com/stats/players/pts/%d' %i)[0])

# 所有数据纵向合并为数据框
players = pd.concat(table)
# 变量重命名
columns=['排名','球员','球队','得分','命中-出手','命中率','命中-三分','三分命中率','命中-罚球','罚球命中率','场次','上场时间']
players.columns=columns
players.drop(0,inplace=True)
print(players)
players.to_csv(r"C:\Users\Administrator\Desktop\小论文代码\players.csv",encoding='utf_8_sig')

将结果写入本地文件players.csv，如下图所示

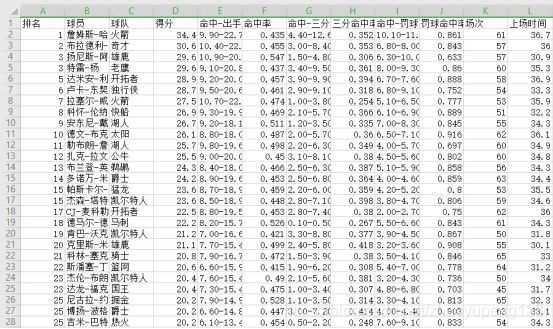
原始数据中命中率的格式为x%，需要进行标准化处理转化为数值形式，小数点后保留3位小数。

2.模型构建

模型的构建主要包括两部分：
(1)根据所获数据集，对球员进行聚类分群；
(2)结合分类结果对球员状态进行分析，分析球员价值。

2.1球员聚类

最佳k值的确定

  本文使用了两种常用的评估方法，用于确定最佳k值：“簇内离差平方和拐点法”、“轮廓系数法”。
①　拐点法：在不同的k值下计算簇内的离差平方和，然后通过可视化的方法找到“拐点”所对应的k值。

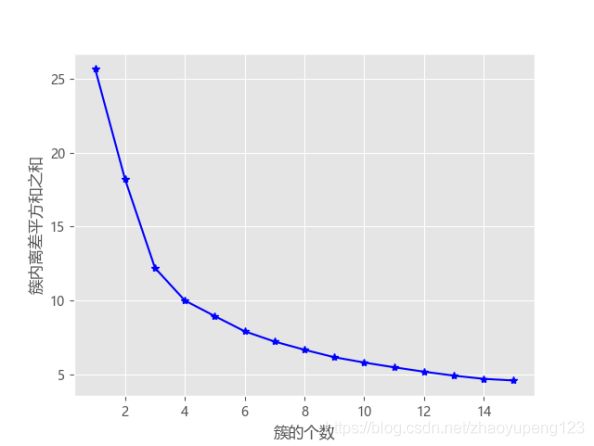
  通过离差平方和的折线图我们能发现k值最好取在3、4、5之间，但还是很难通过观察找到最佳的k值。于是我们采用第二种方法（轮廓系数法）来进行k值的确定。
②　轮廓系数法：该方法综合考虑了簇的密集性与分散性两个信息，如果数据集被分割为理想的k个簇，那么对应的簇内样本会很密集，而簇间样本会很分散，轮廓系数的计算公式如下：

其中，a(i)体现了簇内的密集性，代表样本i与同簇内其他样本点距离的平均值；b(i)反映了簇间的分散性，其计算过程是：样本i与其他非同簇样本点距离的平均值，然后从平均值中挑选出最小值。
有关轮廓系数的计算，我们可以直接调用sklearn子模块metris中的函数silhouette_score。该函数接受的聚类簇数必须大于或等于2，下面基于该函数重新自定义一个函数，用于绘制不同k值下对应轮廓系数的折线图，具体代码如下所示：

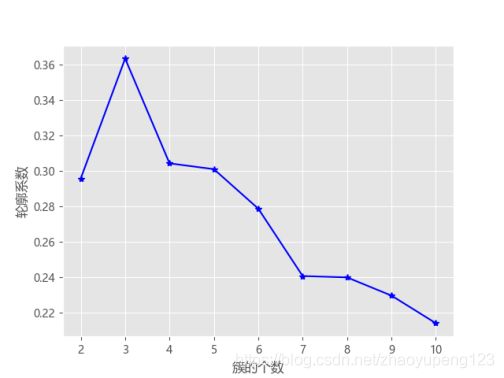
  观察不同k值轮廓系数折线图，我们能发现k=3时轮廓系数最大，总体随k值增大而递减，但是最大也只有0.36左右，并不能达到约等于1的理想值，所以我们综合轮廓系数法和拐点法，在之前的结论3、4、5中选出最合适的k值：3。

聚类分析

在上面的结论下，我们把该数据聚集为三类：

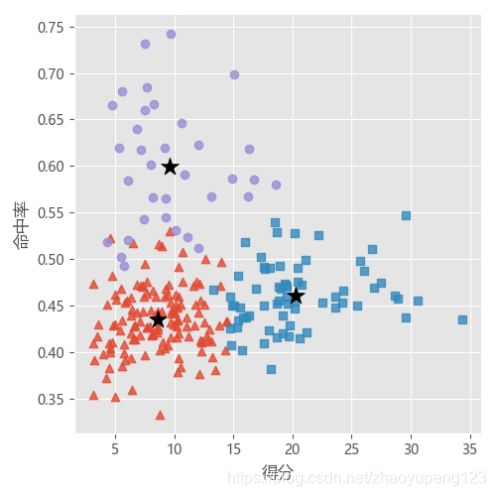
  从最终的结论图中我们不难发现，第一类红色部分表示球员的得分相对较低且命中率也较低，我们可以总结为得分能力不强的球员，总样本中占136人。第二类蓝色正方形表示的球员得分高、命中率高，我们总结其为职业生涯巅峰球员，各个球队的得分机器，样本中有68人。第三类用紫色圆点表示的球员得分低但命中率很高，我们可以归类为上场及进攻次数较少的球员，占33人。
最后附上聚类分析的代码：

# 读取球员数据
import pandas as pd
import matplotlib.pyplot as plt
import numpy as np
players = pd.read_csv(r'players.csv',encoding='gbk')
players.head()
# 中文和负号的正常显示
plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
plt.rcParams['axes.unicode_minus'] = False
#绘制得分与命中率的散点图
import seaborn as sns
sns.lmplot(x = '得分',y = '命中率',data = players,
           fit_reg = False, scatter_kws = {'alpha':0.8,'color':'steelblue'})
plt.show()

# 构造自定义函数，用于绘制不同k值和对应总的簇内离差平方和的折线图
def k_SSE(X, clusters):
    # 选择连续的K种不同的值
    K = range(1,clusters+1)
    # 构建空列表用于存储总的簇内离差平方和
    TSSE = []
    for k in K:
        # 用于存储各个簇内离差平方和
        SSE = []
        from sklearn.cluster import KMeans
        kmeans = KMeans(n_clusters=k)
        kmeans.fit(X)
        # 返回簇标签
        labels = kmeans.labels_
        # 返回簇中心
        centers = kmeans.cluster_centers_
        # 计算各簇样本的离差平方和，并保存到列表中
        for label in set(labels):
            SSE.append(np.sum((X.loc[labels == label,]-centers[label,:])**2))
        # 计算总的簇内离差平方和
        TSSE.append(np.sum(SSE))

    # 中文和负号的正常显示
    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
    plt.rcParams['axes.unicode_minus'] = False
    # 设置绘图风格
    plt.style.use('ggplot')
    # 绘制K的个数与GSSE的关系
    plt.plot(K, TSSE, 'b*-')
    plt.xlabel('簇的个数')
    plt.ylabel('簇内离差平方和之和')
    # 显示图形
    plt.show()


from sklearn import preprocessing
# 数据标准化处理
X = preprocessing.minmax_scale(players[['得分','罚球命中率','命中率','三分命中率']])
# 将数组转换为数据框
X = pd.DataFrame(X, columns=['得分','罚球命中率','命中率','三分命中率'])
k_SSE(X, 15)

# 构造自定义函数，用于绘制不同k值和对应轮廓系数的折线图
def k_silhouette(X, clusters):
    K = range(2,clusters+1)
    # 构建空列表，用于存储个中簇数下的轮廓系数
    S = []
    for k in K:
        from sklearn.cluster import KMeans
        kmeans = KMeans(n_clusters=k)
        kmeans.fit(X)
        labels = kmeans.labels_
        # 调用字模块metrics中的silhouette_score函数，计算轮廓系数
        from sklearn.metrics import silhouette_score
        S.append(silhouette_score(X, labels, metric='euclidean'))

    # 中文和负号的正常显示
    plt.rcParams['font.sans-serif'] = ['Microsoft YaHei']
    plt.rcParams['axes.unicode_minus'] = False
    # 设置绘图风格
    plt.style.use('ggplot')
    # 绘制K的个数与轮廓系数的关系
    plt.plot(K, S, 'b*-')
    plt.xlabel('簇的个数')
    plt.ylabel('轮廓系数')
    # 显示图形
    plt.show()

k_silhouette(X, 10)

# 将球员数据集聚为3类
from sklearn.cluster import KMeans
kmeans = KMeans(n_clusters = 3)
kmeans.fit(X)
# 将聚类结果标签插入到数据集players中
players['cluster'] = kmeans.labels_
# 构建空列表，用于存储三个簇的簇中心
centers = []
for i in players.cluster.unique():
    centers.append(players.loc[players.cluster == i,['得分','罚球命中率','命中率','三分命中率']].mean())
# 将列表转换为数组，便于后面的索引取数
centers = np.array(centers)

# 绘制散点图
sns.lmplot(x = '得分', y = '命中率', hue = 'cluster', data = players, markers = ['^','s','o'],
           fit_reg = False, scatter_kws = {'alpha':0.8}, legend = False)
# 添加簇中心
plt.scatter(centers[:,0], centers[:,2], c='k', marker = '*', s = 180)
plt.xlabel('得分')
plt.ylabel('命中率')
# 图形显示
plt.show()

res0Series = pd.Series(kmeans.labels_)
res0 = res0Series[res0Series.values == 0]
print(players.iloc[res0.index])

res0Series = pd.Series(kmeans.labels_)
res0 = res0Series[res0Series.values == 1]
print(players.iloc[res0.index])

res0Series = pd.Series(kmeans.labels_)
res0 = res0Series[res0Series.values == 2]
print(players.iloc[res0.index])

参考文献
https://blog.csdn.net/liuzuoping/article/details/103167684
https://blog.csdn.net/JAVA_wangyi/article/details/106032641