《深度学习》学习笔记
本文是李宏毅教授《机器学习》课程的学习笔记,简要地介绍了深度学习的基本概念及常见网络架构,包括卷积神经网络、自注意力机制、Transformer、BERT、生成对抗网络、领域自适应网络等,此外还简单地介绍了强化学习和元学习,有利于大家快速了解深度学习的主要技术。本文尽可能地避开了数学,主要讲网络架构的设计思想,这对于一个刚接触深度学习的初学者来说还是比较友好的。
此外,李教授的课程生动有趣,深入浅出,强烈推荐各位想了解深度学习的同仁们去看看他的视频。
文章目录
- 1.什么是人工智能?
- 2.什么是机器学习?
-
- 2.1 机器学习概述
- 2.2 机器学习的三个基本步骤
-
- 2.2.1 定义一个包含未知参数的Function
- 2.2.2 定义一个损失函数
- 2.2.3 优化Function的参数
- 2.3 模型的测试与修正
- 3.什么是深度学习?
-
- 3.1 深度学习概述
- 3.2 神经元模型
- 3.3 神经元的连接
- 3.4 神经网络的训练
- 4.卷积神经网络(Convolutional Neural Networks, CNN)——更有效率地提取特征
-
- 4.1 全连接神经网络的问题
- 4.2 利用“感受野”看图片的局部
- 4.3 神经元的参数共享
- 4.4 对CNN的总结
- 4.5 CNN的应用
- 5.自注意力机制(self-attention)——考虑全局又聚焦重点
-
- 5.1 自注意力机制概述
- 5.2 向量相关性计算
- 5.3 基于注意力分数抽取向量信息
- 5.4 自注意力机制中的矩阵计算
-
- 5.4.1 计算矩阵 K 、 V 、 Q K、V、Q K、V、Q
- 5.4.2 计算注意力分数矩阵 A ′ A' A′
- 5.4.3 计算输出矩阵 O O O
- 5.4.4 自注意力矩阵计算总结
- 5.5 多头自注意力机制
- 6.Transformer——实现“序列to序列”的转换
-
- 6.1 Transformer 概述
- 6.2 Transformer的Encoder
- 6.3 Transformer的Decoder
-
- 6.3.1 Decoder的自回归(Autoregressive)机制。
- 6.3.2 Decoder的结构
- 7.BERT——自监督学习的典范
-
- 7.1 自监督学习的概念
- 7.2 BERT概述
- 7.3 BERT的训练
-
- 7.3.1 Masked Language Model
- 7.3.2 Next Sentence Prediction
- 7.4 BERT的应用
- 8.生成对抗网络(Generative Adversarial Networks,GAN)——让机器学习具有创造力
-
- 8.1生成对抗网络概述
-
- 8.1.1 对“生成”的理解
- 8.1.2 对“对抗”的理解
- 8.2 生成对抗网络的理论基础
- 9.领域自适应(Domain adaption)——实现模型的自适应迁移
-
- 9.1领域自适应网络概述
- 9.2 领域自适应的基本思路
- 9.3 域分类器的引入
- 10.强化学习(Reinforcement Learning, RL)——让AlphaGo进化得比人类更强
-
- 10.1 题外话:人类棋手的最后赞礼
- 10.2 强化学习概述
-
- 10.2.1 强化学习的目标也是要找一个Function
- 10.2.2 强化学习的三个基本步骤
-
- 10.2.2.1 定义一个function
- 10.2.2.2 定义一个损失函数
- 10.2.2.3 优化参数
- 10.3 Policy Gradient
-
- 10.3.1 Actor的行为控制
- 10.3.2 优势函数 A t A_t At的确定
- 10.3.3 参数更新算法
- 10.4 Actor-Critic 算法
-
- 10.4.1 价值函数的概念
- 10.4.2 价值函数 V θ ( s ) V^\theta(s) Vθ(s)的训练方法
-
- 10.4.2.1 基于蒙特卡洛(MC)的方法
- 10.4.2.2 基于时序差分(TD)的方法
- 10.4.3 价值函数 V θ ( s ) V^\theta(s) Vθ(s)在优势函数上的应用
- 11.元学习(Meta-learning)——让机器学习如何学习
-
- 11.1 元学习概述
- 11.2 MAML
-
- 11.2.1 MAML概述
- 11.2.2 MAML的训练
- 11.3 元学习在N-ways K-shot上的应用
1.什么是人工智能?
现在“智能”两个字已经泛滥了,无论哪个领域都要赶个时髦,给自己的产品打上“智能”的标签。例如“智能台灯”、“智能水杯”等,这些东西无非是连接了WiFi,能够远程控制或者简单的自动控制而已。它们是不是智能的非常值得商榷。
所谓“智能”目前并没有一个明确的定义。但是我们可以肯定的是:“智能”是对人类的模拟,要让机器像人一样去思考、去行动。
像人一样思考的前提是要知道人类是怎么思考的,所以需要捕捉我们自身的思维过程甚至是生物上的化学反应过程。当前兴起的认知科学就是要把来自AI的计算机模型与来自心理学的实验技术相结合,试图构建一种精确且可测试的人类思维理论。但是目前该技术未见成熟,所以目前人工智能做的都是让机器像人一样去行动。
像人一样去行动,人工智能需具备以下能力:
- 自然语言处理可以使之与人类对话
- 知识表示可以存储它所知道的或学习到的知识
- 自动推理可以通过对环境的感知以及自身的知识储备推理出新的结论
- 机器学习以适应新情况并作出预测
- 机器视觉像人一样感知物体
- 机器人学像人一样移动或者操作
以上6各方面囊括了人工智能的大部分研究内容。
像人一样行动的机器我们称其为智能体(Agent)。一个理性的智能体我们期望它应当能够感知环境、持续适应变化、自主操作。
(1)感知环境很好理解,给智能体安装传感器,就可以将环境信息转换为数字信息并让智能体吸收了。当然,环境是广义的,对于一个纯软件的智能体,计算机所构成的信息环境也是智能体的环境,所以文档输入、网页浏览等都属于环境感知。
(2)持续适应变化是啥意思呢?举个例子,一个小孩还从没见过猫和狗,在一次散步时,你发现有一只猫和一只狗,你就告诉他这是猫,那是狗。下次散步时,又见到了猫和狗,但猫不是那只猫了,狗也不是那只狗了。你问小孩哪知是小狗呀?小孩准确的回答了你的问题。你非常开心,然后赞道“蛋蛋宝贝真聪明!”。尽管环境变了,我们人类往往能根据经验适应环境的变化做出正确的判断和合理的行为,当然我们希望我们创造的智能体也具备上述能力。要做到这点,要求智能体必须学习,从纷繁复杂的事物中提取一般的事物规律。所以,没有学习的“智能”我们都可以持怀疑态度。
(3)自主操作和自动操作有很大的区别。现在很多商家滥用“智能”就是混淆了自主和自动的区别。自动化是基于规则工作的,人类将先验知识设计成各种规则并注入到机器中,使机器可以代替人自动化地执行一些工作,从而提高生产效率。所以,自动化的选择结果几乎都是确定的,是我们可以预知的。自主不完全依托于人类的经验知识,它可能会产生新的知识,它的很多行为不是预期的程序化设计,而是不可预期的非程序化。要实现自主操作,智能体需要学习,它需要从感知的环境中学习知识,而不是人类给注入的先验知识。
可见,学习是智能体的一个重要表现,也是人工智能中的最重要研究内容。那么,如何才能让机器学习呢?
2.什么是机器学习?
2.1 机器学习概述
在一次散步时,我们告诉一个从没见过猫狗的小朋友这是猫、那是狗,小朋友在下一次见到猫狗时就能基于上一次的经验准确的分辨出猫和狗了,这是我们人类的学习。所谓机器学习,就是希望机器能够像人类一样从经验中学习知识,当遇到类似的新情况时能够做出有效的决策。在计算机系统中,“经验”通常以“数据”的形式存在。因此,机器学习的主要内容,是关于在计算机上从数据中产生Function的算法,这个Function的作用是将将输入映射成合理的输出。例如给Function输入猫的图片,Function能够正确的输出“猫”的判别。在机器学习中,我们通常把Function也叫做模型(Model)。
因此,简单点来讲,机器学习就是要从数据中找到一个Function,可以将输入映射成合理的输出。用数学来表示就是 y = f ( x ) y=f(x) y=f(x)机器学习就是要找到这个 f f f,其中 x x x是输入, y y y是输出。机器学习找这个 f f f的过程包含三个基本的步骤:定义一个包含未知参数的Function、定义一个损失函数、优化Function的参数。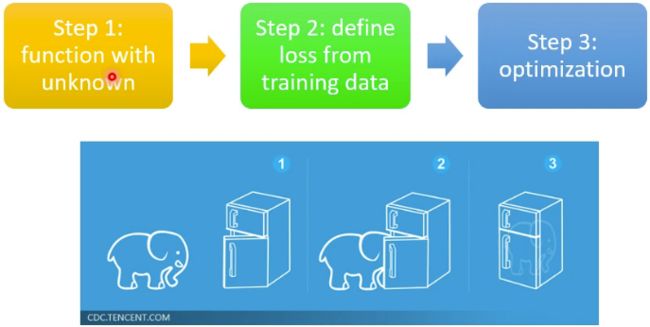
下面通过李宏毅老师的关于访问流量预测例子来说明这三个步骤,即用当天的访问流量预测第二天的访问流量:输入是当天的流量,输出是第二天的流量。
2.2 机器学习的三个基本步骤
2.2.1 定义一个包含未知参数的Function
假设第二天的视频访问流量和前一天的视频访问流量呈线性关系,即, y = b + w x 1 y=b+wx_1 y=b+wx1其中 x 1 x_1 x1是前一天的视频访问量,即函数的输入, y y y是预测的第二天的视频访问量,即函数的输出。 b , w b,w b,w是函数的未知参数,在机器学习里面我们常把 w w w称为权值(Weight),把 b b b称为偏置(Bias)。
那么是如何定义出这个函数的呢?是基于对这个求解问题的本质了解确定的,也就是领域知识。所以在确定Function的架构时,我们往往需要具备应用领域的专门知识。当然,即使具有领域的专门知识,函数架构的设计不是一蹴而就的,是一个不断修正的过程。即刚开始初步设计一个架构,可能不太理想,然后对其改进,通过反复的迭代,最后得到一个比较满意的Function架构。
2.2.2 定义一个损失函数

损失函数是一个有关参数 b , w b,w b,w的函数,它反映模型输出的好坏。我们期望模型的估测值和真实值之间的差距要越小越好。这个差距用 e e e表示,计算 e e e的方式有多种。对于数值输出,常见的计算方式有平均绝对误差(MAE)和均方误差(MSE):
MAE: e = ∣ y − y ^ ∣ \text{MAE: }e=\mid y-\hat{y}\mid MAE: e=∣y−y^∣ MSE: e = ( y − y ^ ) 2 \text{MSE: }e=(y-\hat{y})^2 MSE: e=(y−y^)2
上面 y y y表示真实值, y ^ \hat{y} y^表示模型的估测值。在这道例题中,李宏毅老师选择了MAE。如果输出是概率分布,例如分类问题,往往采用交叉熵(Cross Entropy): e = − ∑ m = 1 M y c log p c e=-\sum_{m=1}^M{y_c\log{p_c}} e=−m=1∑Myclogpc
其中, M M M表示类别的数目; y c y_c yc是一个符号函数(0或1),如果样本的真实类别等于 c c c取1,否则取0; p c p_c pc模型输出样本属于类别 c c c的预测概率。
假设有 N N N个训练数据,那么损失函数 L L L可以定义为,
Loss: L = 1 N ∑ n = 1 N e n \text{Loss: }L=\frac{1}{N}\sum_{n=1}^N{e_n} Loss: L=N1n=1∑Nen
每一对确定的参数 b , w b,w b,w,就可以计算出一个Loss。Loss越小说明模型估测的结果越接近于真实值,表明参数 b , w b,w b,w的值越好。
上述只是个简单的例子,在实际应用过程中,损失函数的定义往往会要复杂得多,也是影响机器学习好坏的一个关键因素。
2.2.3 优化Function的参数
参数优化就是要找到最佳的参数 b , w b,w b,w,使Loss最小,即, w ∗ , b ∗ = a r g min w , b L w^* ,b^*=arg\underset{w,b}{\text{min}}L w∗,b∗=argw,bminL那么如何找呢?最为常用的方法就是梯度下降法(Gradient Descent)。梯度下降法可以理解为:我们从山上的某一点出发,找一个向下最陡的坡走一步(也就是找负梯度方向),到达一个点之后,再找向下最陡的坡,再走一步,直到我们不断的这么走,走到最“低”点。其过程主要包括:
- 初始化参数 b 0 , w 0 b_0,w_0 b0,w0,初始化参数可以是自己定的,也可以是随机的。
- 计算损失函式在 b 0 , w 0 b_0,w_0 b0,w0处对 b , w b,w b,w的微分值,然后更新参数值:
w 1 ← w 0 − η ∂ L ∂ w ∣ w = w 0 , b = b 0 w^{1} \leftarrow w^{0}-\left.\eta \frac{\partial L}{\partial w}\right|_{w=w^{0}, b=b^{0}} w1←w0−η∂w∂L∣∣∣∣w=w0,b=b0
b 1 ← b 0 − η ∂ L ∂ b ∣ w = w 0 , b = b 0 b^{1} \leftarrow b^{0}-\left.\eta \frac{\partial L}{\partial b}\right|_{w=w^{0}, b=b^{0}} b1←b0−η∂b∂L∣∣∣∣w=w0,b=b0
其中 η \eta η指学习速率,决定了下坡时每走一步跨多大。 - 重复上一步,反复迭代更新 b , w b,w b,w,直到损失函数不再减小。
梯度下降法很简单,但是基本上能应用到绝大部分的深度学习框架上。梯度下降的微分值也不需要我们自己手动去算,我们借助于计算机即可,Python中的Pytorch都提供了很好的工具帮助我们计算微分对参数进行迭代。
当然,梯度下降法也会存在一些问题,最常见的一个问题就是陷入局部最优。因此梯度下降法有很多变形,例如随机梯度下降(SGD)、自适应梯度下降等。
2.3 模型的测试与修正
前面提到了一个函数 f f f的架构设计,也就是模型架构的设计不是一蹴而就的,往往需要根据多次迭代不断修正才会得到比较好的模型。那么如何评价一个模型的好坏呢?前面说到我们希望模型的估测值要和真实值越接近越好,所以我们可以用平均绝对误差(MAE)和均方误差(MSE)来衡量一个模型的好坏。
但是要注意的是我们让机器学习的目的是对未来的事情进行预测,而不是对已经发生的事情进行预测。也就是说我们不能再用训练数据去测试模型的好坏了,而要用新的、未参与训练的数据进行测试。所以我们在做机器学习的时候,往往会把数据集分成训练数据集和测试数据集。训练数据集用于优化模型参数,测试数据集用于测试模型的好坏。例如上面访问流量预测的例子,将2017年—2020年所有的访问流量数据作为训练数据,2021年1月1日—2021年2月14日作为测试数据。这道理子计算得到,在训练数据集上的MAE是0.48k,在测试数据集上的MAE是0.58k。
如果感觉上面的误差有点大,那么如何优化模型架构使误差更小呢?这需要利用领域知识对问题进行分析。比如上面这个例子,将2021年1月1日—2021年2月14日的数据画在图上如下图所示,发现访问流量使呈周期性变化的,周期是一个星期,周末的访问流量明显要低于周内,因为周末休息就懒得学习《机器学习》了。
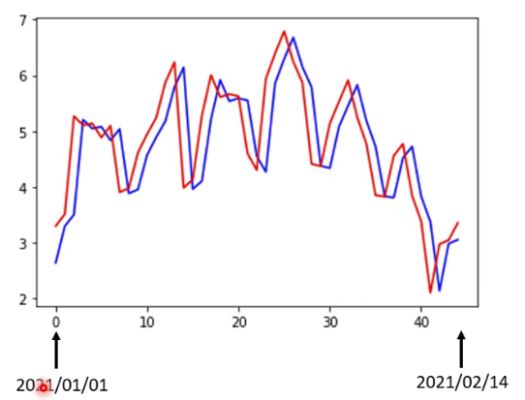
既然访问流量是按7天一个周期变化的,那么预测第二天的流量只看前一天不太合理,应该看7天的,所以就建立了一个新的模型, y = b + ∑ j = 1 7 w j x j y=b+\sum_{j=1}^{7} w_{j} x_{j} y=b+j=1∑7wjxj其中 x j x_{j} xj代表前第 i i i天的访问流量。经过改进之后,在训练数据集上的MAE是0.38k,在测试数据集上的MAE是0.49k。可见模型的准确度有所提升了。
如果把时间拉得更长,让机器看前28天的访问流量,得到的结果是在训练数据集上的MAE是0.33k,在测试数据集上的MAE是0.46k,又有所提升。如果看56天的,则MAE分别是0.32k,0.46k,没什么提升了,可见增加天数并不是万能的。
上面的模型一般化之后可以表示为 y = b + ∑ j = 1 N w j x j y=b+\sum_{j=1}^{N} w_{j} x_{j} y=b+j=1∑Nwjxj这个模型在机器学习中称为线性模型(Linear Model),其中 x j x_{j} xj是输入,也称为特征值, N N N代表特征值的个数,也称为特征值维度, w j w_j wj是权值(Weight), b b b是偏置(Bias)。
3.什么是深度学习?
3.1 深度学习概述
深度学习本质上是神经网络。只是神经网络这个词在80、90年代的时候被搞臭了,因为当时神经网络被吹捧得过于浮夸,最后弄得大家都很厌恶神经网络这个词。只要把神经网络写到论文中,一般要被拒的。后来,为了重振神经网络的雄风,需要弄个新的、高大上的名字来替代。由于计算机性能越来越好,可以搞的网络层级越来越多,于是人们就给神经网络取了个比较牛的名字叫做“深度学习”。
3.2 神经元模型
神经网络顾名思义就是对人类神经的一个模拟,当然只是形式上的模拟。我们知道,人的神经网络由千亿个神经元组成,而每一个神经元由树突、细胞体、轴突组成,树突用来接受传入的信息,而轴突用来将信号传递给其他神经元,通过突触,神经元被连接到一起,形成复杂的网络。
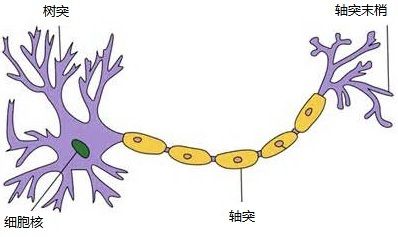
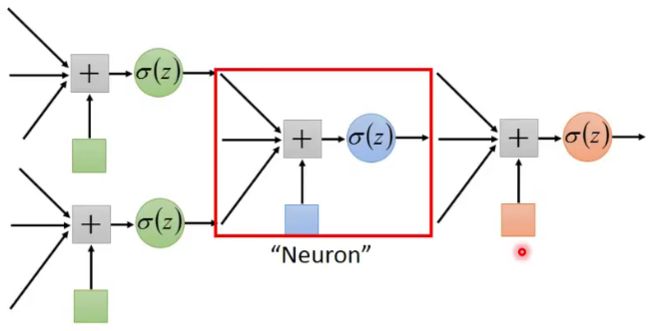
人工神经网络对神经元进行模拟,建立了神经元模型,如下图。神经元模型包含输入、输出与计算功能,输入可以类比为神经元的树突,而输出可以类比为神经元的轴突,计算则可以类比为细胞体。

图中这个神经元模型包括三个输入,一个计算,和一个输出。图中从输入到求和就对应着前面提到的线性模型,三条边包含了三个权值,下面的蓝色块是偏置,求和项就是 b + ∑ j = 1 3 w j x j b+\sum_{j=1}^{3} w_{j} x_{j} b+∑j=13wjxj。但是注意到求和之后并未直接输出,而是经过了一个非线性函数 σ ( z ) \sigma(z) σ(z)进行计算后输出的,这是为什么呢?这是因为线性模型过于简单,缺乏灵活性,比如下面这个图,无论怎么调整 w w w和 b b b,都无法拟合出红色这条线,始终是存在偏差的。所以我们需要更加复杂的、更富有弹性的函数,因此就增加了非线性函数的计算。

这个非线性函数也被称为激活函数。常见的激活函数有, Sigmoid: S ( x ) = 1 1 + e − x \text{Sigmoid: } S(x)=\frac{1}{1+e^{-x}} Sigmoid: S(x)=1+e−x1 ReLu: f ( x ) = max ( 0 , x ) \text{ReLu: }f(x)=\text{max}(0, x) ReLu: f(x)=max(0,x)这两个函数的微分比较好计算,我想是它们称为常见激活函数的一个重要原因。将线性模型的输出在输入到上述非线性函数中我们就可以得到更加具有弹性的模型了。如果激活函数使用Sigmoid函数,那一个神经元的数学表达式就可以表达为, y = 1 1 + e − ( b + ∑ j = 1 N w j x j ) y=\frac{1}{1+e^{-(b+\sum_{j=1}^{N} w_{j} x_{j})}} y=1+e−(b+∑j=1Nwjxj)1
一个神经元的输出可作为令一个神经元的输入,这就好比上一个神经元的轴突末梢会与下一个神经元的树突相连,用来传递信息,这样就将两个神经元连接在一起了,如下图所示。
3.3 神经元的连接
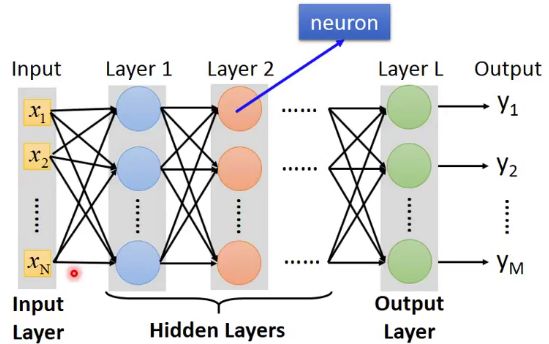
我们采用不同的方式对神经元进行连接就会得到不同的网络架构。比如我们将神经元排成一层一层的,上一层的所有神经元连接到下一层的所有神经元,就形成了如下图所示的网络。我们将这样的网络称为前向全连接网络。一般把网络第一层称为输入层,最后一层称为输出层,中间的层称为隐藏层。
后来人们发现隐藏层叠得越多,网络的性能就越好。例如,在一个图片识别的公共测试集上,2012年AlexNet共8层,错误率为16.4%,2014年VGG共19层,错误率为7.3%,2014年GoogleNet共22层,错误率6.7%,2015年Residual Net有152层,错误率降到了3.57%。因此,现在的网络都是越叠越高,这种叠了很多层的神经网络就称为“深度学习”。
3.4 神经网络的训练
在构建了这个模型之后,就可以基于损失函数对参数进行优化了,采用的方法就是梯度下降法。但是我们注意到当神经网络叠的层次比较多的时候,参数的数目是爆炸性增长的,比如现在的语音识别网络简单一点的也有七八层,每一层有上千个神经元,参数量就达到上百万个。如果直接采用梯度下降法,每迭代一步都对所有参数进行微分计算,计算量将时巨大的!为了使梯度下降法更有效率,一种叫做后向传播(backpropagation)的算法被提出。后向传播本质上也是一种梯度下降法,但是要讲清楚它非常麻烦,如果感兴趣可以观看李宏毅老师的视频,他讲得还是很清楚的。
现在我们再来看一下用神经网络的方法解决李宏毅老师提出的访问流量预测问题,他做实验的结果如下。从表中可以看出随着网络层次的增加,在训练集上的误差是越来越小的,但是在测试集上并不是这样的。可以看到,4层网络时误差比3层网络的误差还要大。像这种训练误差在减小,测试误差反而增大的情况,在机器学习中称为过拟合。造成过拟合的原因主要有训练数据不足、分布不合理、噪声很强等,或者模型过于复杂等。至于如何解决过拟合问题,李宏毅老师的视频中都有,如果感兴趣可以去学习一下。

4.卷积神经网络(Convolutional Neural Networks, CNN)——更有效率地提取特征
4.1 全连接神经网络的问题
图像识别问题本质上就是分类问题,比如我们要区分猫和狗,那么我们就需要构建一个模型,将照片丢进去后,模型能输出猫或者狗的概率有多大。在做图像识别时首要的就是要提取图片的特征,那么如何提取图片的特征呢?前面讲到了前向全连接网络,我们可以尝试用前向全连接网络提取。假设图片的像素是100*100,如果如片是彩色的,每个像素都有RGB三种颜色的数值。因此,一张图片是有一个三维向量构成的,一维是长100,一维是宽100,还有一维是R、G、B 3个通道(channels)。把这个三维向量拉直作为一个一维向量,长度就是100*100*3。

假设全连接网络的输入层有100个神经元,那么输入层的权值参数 w w w(Weight)的个数就等于 100 ∗ 100 ∗ 3 ∗ 100 = 3 × 1 0 6 100*100*3*100=3\times 10^6 100∗100∗3∗100=3×106这个参数量是巨大的,参数数目越多导致模型就越复杂,就更容易产生过拟合问题。另外参数量太大,也会导致计算量巨大。

采用前向全连接网络提取图片特征是不可取的,那么如何更加有效率地提取图片特征呢?前面提到了设计一个网络的架构,需要分析网络应用领域的专门知识,在这里我们就需要分析图片的特性。
4.2 利用“感受野”看图片的局部
我们在区分一张图片时,我们观察的往往是图片的局部的、最重要的特征。 比如图片上是一只鸟,我们可能通过嘴巴、眼睛、爪子等就可以判断出是一只鸟了。因此,输入层的每一个神经元没有必要看图片的全局,只需要看一个局部就行了。

根据这个特性,我们就可以对网络进行简化了。一个神经元不看图片的全局,而是看图片的一个局部,我们将这个局部称为神经元的感受野(receptive field),比如下图所示的神经元感受野是3*3*3的,表示宽度、长度、通道数都是3。不同神经元的感受野可以存在重叠区域甚至是完全相同的,这个在于个人的设计,但是有一个常用的设计做法。
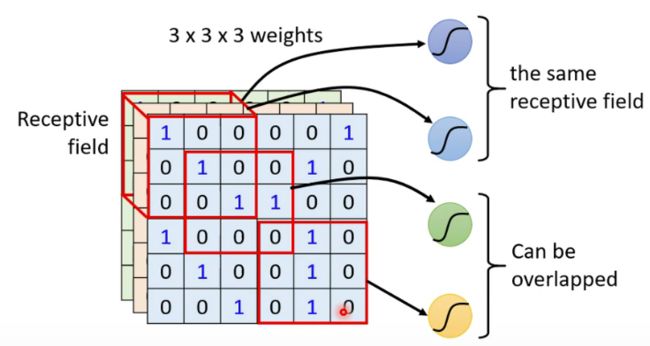
这个常用的设计做法如下图所示。所有神经元的感受野大小是一样的,且感受野包含图片的所有通道,比如下图所设计的感受野大小为3*3*3。这些感受野的排布方式如下:左上角的感受野向右滑动2个像素(当然也可以滑动1个像素,滑动的步长(stride) 时自定义的),形成一个新的感受野,这样两个感受野就有1个像素的宽度重叠,然后新的感受野再向右滑动2个像素,又形成了一个新的感受野,这样反复滑动并形成新的感受野,直到滑到图片的最右端,这时候感受野可能超出了图片的区域,对超出部分采取的策略是填0,称为“padding"。在完成了第一行滑行后,感受野在往下滑两个像素,然后重复上述过程,然后再下滑直到感受野到达图片低端,这样所有的感受野就可以覆盖整张图片了。比如图中图片的像素是6*6*3的,感受野大小为3*3*3,滑动步长为2,那么总共就会有9个感受野。假设每一个感受野有一个神经元进行观测,那么就会有9个神经元,每个神经元的参数是9个权值加1个偏置,那么就总共有90参数。
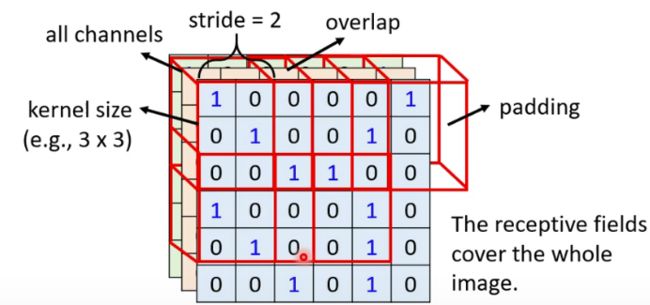
4.3 神经元的参数共享
在两张不同的图片上,同一个特征区域可能处于不同位置。 比如鸟嘴的局部特征区域在下面这两张图上就处在不同的位置上。那么如何才能让两个不同的神经元在看到这两个不同的感受野时,能产生一致的特征值呢?

一个较好的办法就是参数共享,即这两个神经元的参数设置成一样的,如下图所示两个不同感受野的神经元的参数是一样的。这两个神经元的参数一样不代表输出也会一样,因为不同的感受野输入的值是不一样的。

前面讲到通过滑动的方式排布的感受野可以覆盖整个图片,假设每一个感受野有一个神经元进行观测,我们让所有的神经元参数共享。这样就相当于一个神经元每次只看一个局部,但是通过滑动扫描的方式将所有局部看了一遍,就等于把图片的整体看了一遍,这是合理的。参数共享之后参数的数量和神经元(感受野)的个数无关了,只和感受野的大小有关,比如针对6*6*3的图片,尽管通过滑动有9个感受野,对应9个神经元,但是这些神经元的参数是一样的,因此参数的个数就只有9个权值加1个偏置。
可以看出,通过局部感受野和参数共享的简化方式,参数的量已经大幅缩减了。但是还存在一个问题,一个神经元可能指对某个或某部分局部特征比较敏感,比如说只对鸟嘴比较敏感,而对鸟抓不敏感,那么就可能会丢失一些特征。那么如何做呢?一个办法是让多个神经元观测同一个感受野,这些神经元是不共享参数的。这样有的神经元可能对鸟嘴比较敏感,而有的神经元对鸟爪比较敏感。至于每个感受野设置多少个不同的神经元,是个人决定的。
4.4 对CNN的总结
对上面的内容进行一个总结:
(1)我们设置一个局部感受野,假设感受野的大小为W*H*C,其中W表示感受野的宽度,H表示感受野的高度,C表示感受野的通道数。那么对应的神经元的参数的个数就为:W*H*C个权值加1个偏置。在卷积神经网络中,我们称这样一个神经元为一个滤波器(filter)。
(3)我们通过滑动的方式让感受野铺满整个图片,假设图片的尺寸是W1*H1*C,滑动步长为S,零填充的数量为P。假设感受野的个数是W2*H2,其中, W 2 = ( W 1 − W + 2 P ) / S + 1 W2=(W1-W+2P)/S+1 W2=(W1−W+2P)/S+1 H 2 = ( H 1 − H + 2 P ) / S + 1 H2=(H1-H+2P)/S+1 H2=(H1−H+2P)/S+1
(4)我们让所有感受野的观测滤波器参数进行共享,即相当于一个滤波器通过滑动扫描的方式扫描了所有感受野。
(5)我们设置多个滤波器,假设滤波器的个数为K,这K个滤波器都通过滑动扫描的方式扫过整个图片。此时参数的个数为:(W*H*C+1)*K。
(6)由于每个滤波器每经过一个感受野都会进行一次计算输出一个值,所以输出的维度为:W2*H2*K。我们将这个输出称为特征图,所以特征图宽度为W2,高度为H2,通道数C2=K。
举个例子: 假设某个图片的大小是100*100*3,设置滤波器的大小为3*3*3,滤波器的个数为64,设置步长S=1,设置零填充的数量为P=0。那么卷积神经网络的参数为, ( 3 × 3 + 1 ) × 64 = 640 (3\times3+1)\times64=640 (3×3+1)×64=640相比前向全连接 3 × 1 0 6 3\times 10^6 3×106个参数,参数的个数缩小了几个数量级。
输出特征图的宽度和高度均为, W 2 = H 2 = ( 100 − 3 + 0 ) / 1 + 1 = 98 W2=H2=(100-3+0)/1+1=98 W2=H2=(100−3+0)/1+1=98输出特征图的通道数为, C 2 = 64 C2=64 C2=64所以输出特征图的维度为98*98*64。
如果在上面输出的基础上再叠加一层卷积神经网络,滤波器的设置宽和高可以不变,但是通道数不再是3了,而是变成64了,因为输入特征图的通道数已经变64了。假设滤波器的大小为3*3*64,滤波器的个数为32,设置步长S=1,设置零填充的数量为P=0。可以计算出来,新的输出特征图的维度是96*96*32。
4.5 CNN的应用
以上就是卷积神经网络(CNN)的解析。但是CNN一般不是单独用的,因为一般提取图片的特征是为了分类,还需要进一步处理,常见的形式如下图所示。
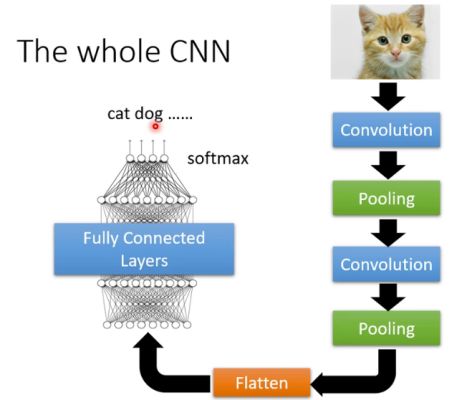
其中Pooling的目的是下采样,以减小特征图的维度。具体的做法是在一个局部区域只取其中一个像素,其他像素都丢弃。比如在一个3*3的局部区域内取最大值,其他值均丢弃,这就是MaxPooling。其中Flatten是拉直,将3维的向量拉成一维向量,然后将这个一维向量输入到一个前向全连接层,以对图片的特征进行高层的融合。最后通过一个softmax层进行分类。
5.自注意力机制(self-attention)——考虑全局又聚焦重点
5.1 自注意力机制概述
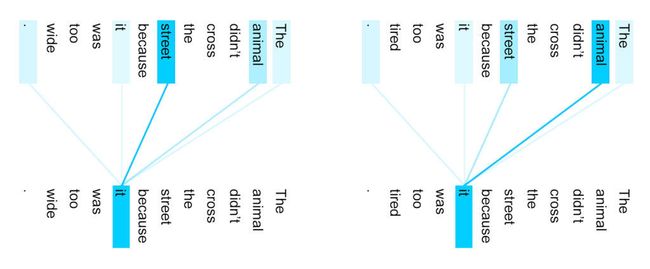
有时候我们期望网络能够看到全局,但是又要聚焦到重点信息上。比如在在做自然语言处理时,句子中的一个词往往不是独立的,和它上下文相关,但是和上下文中不同的词的相关性是不同的,所以我们在处理这个词时,在看到它的上下文的同时也要更加聚焦与它相关性更高的词,这就要用到常说的自注意力机制。比如下面这两幅图,通过自注意力机制处理后,计算出了词间的相关性,可以看到第一个图的it与animal的相关性很强,第二个图it与street的相关性很强。那么如何实现自注意力机制呢?
5.2 向量相关性计算
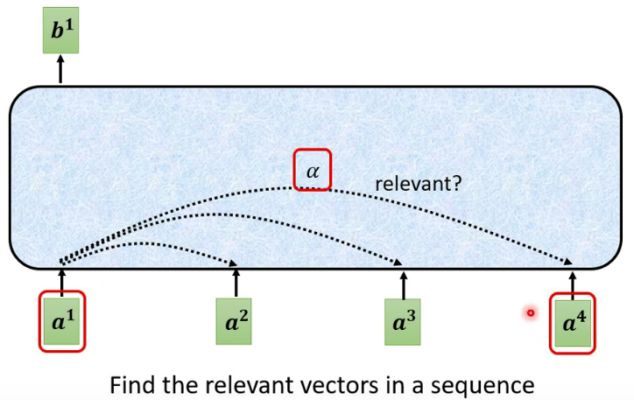
自注意力机制的核心是捕捉向量之间的相关性。比如下面这幅图,输出一个向量 b 1 b^1 b1不只看 a 1 a^1 a1本身,还要看 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4,但是看它们的程度不一样。这就需要分别计算 a 1 a^1 a1与 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4之间的相关性 α \alpha α, α \alpha α越大,相关性越高,给予的重视程度就越高。那么如何让网络自动计算出两个向量之间的相关性呢?
计算两个向量之间的相关性的常见方法是求点积(dot-product),如下图所示。具体的做法是左边的向量乘以一个变换矩阵 W q W^q Wq得到向量 q q q,右边的向量乘以一个变换矩阵 W k W^k Wk得到向量 k k k,然后将向量 q q q和向量 k k k点积就可以得到相关性 α \alpha α。由点积的性质可知,两个向量的相似度越高,点积的值就会越大。当然,计算向量相关性的方法不只点积这一种,也有其他方式,但是点积这种是最常见的。

基于点积计算,我们就可以向量两两之间的关联性了,比如首先分别计算 a 1 a^1 a1与 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4之间的相关性。我们首先将 a 1 a^1 a1乘以变换矩阵 W q W^q Wq得到向量 q 1 q^1 q1,这里的 q 1 q^1 q1向量有个专门的名字,叫做 “query” 。然后将 a 1 a^1 a1、 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4分别乘以变换矩阵 W k W^k Wk得到向量 k 1 , k 2 , k 3 , k 4 k^1,k^2,k^3,k^4 k1,k2,k3,k4,这里的 k i k^i ki向量也有个专门的名字,叫做 “key”。然后将 q 1 q^1 q1和这四个key分别做点积,就得到四个相关性数值 α 1 , 1 , α 1 , 2 , α 1 , 3 , α 1 , 4 \alpha_{1,1},\alpha_{1,2},\alpha_{1,3},\alpha_{1,4} α1,1,α1,2,α1,3,α1,4。求出这四个相关性的值后,然后通过一个Soft-max层进行归一化,得到 α 1 , 1 ′ , α 1 , 2 ′ , α 1 , 3 ′ , α 1 , 4 ′ \alpha^{'}_{1,1},\alpha^{'}_{1,2},\alpha^{'}_{1,3},\alpha^{'}_{1,4} α1,1′,α1,2′,α1,3′,α1,4′,这是最后输出的相关性值,我们将这些值又称为**“注意力分数”**。现在我们得到了 a 1 a^1 a1对 a 1 a^1 a1、 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4之间的注意力分数,那么如何做到考虑全局又聚焦重点呢?

5.3 基于注意力分数抽取向量信息
通过上面计算出的注意力分数 α 1 , 1 ′ , α 1 , 2 ′ , α 1 , 3 ′ , α 1 , 4 ′ \alpha^{'}_{1,1},\alpha^{'}_{1,2},\alpha^{'}_{1,3},\alpha^{'}_{1,4} α1,1′,α1,2′,α1,3′,α1,4′,我们已经知道 a 1 a^1 a1要给予 a 1 a^1 a1、 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4的关注程度了,接下来我们抽取这些向量中重要的信息以输出 b 1 b^1 b1了。具体的做法如下图所示。首先我们再将 a 1 a^1 a1、 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4乘以一个新的变换矩阵 W v W^v Wv得到向量 v 1 , v 2 , v 3 , v 4 v^1,v^2,v^3,v^4 v1,v2,v3,v4,这里的 v i v^i vi向量也有个专门的名字,叫做 “value”。然后将向量 v 1 , v 2 , v 3 , v 4 v^1,v^2,v^3,v^4 v1,v2,v3,v4分别乘以对应的注意力分数 α 1 , 1 ′ , α 1 , 2 ′ , α 1 , 3 ′ , α 1 , 4 ′ \alpha^{'}_{1,1},\alpha^{'}_{1,2},\alpha^{'}_{1,3},\alpha^{'}_{1,4} α1,1′,α1,2′,α1,3′,α1,4′,并进行求和,输出向量 b 1 b^1 b1。从这里可以看出,所有向量都有参与计算,这样就做到了看全局。但是各向量参与计算的程度不一样, α 1 , i ′ \alpha^{'}_{1,i} α1,i′就相当权重值,权重值越大的,对应向量参与计算的程度就越大,最后得到的输出向量 b 1 b^1 b1就和该向量越相似。这样就做到了看全局又聚焦重点。通过上述同样的计算方式,也可以计算得到 b 2 , b 3 , b 4 b^2,b^3,b^4 b2,b3,b4,而且 b 1 , b 2 , b 3 , b 4 b^1,b^2,b^3,b^4 b1,b2,b3,b4是可以并行计算的。以上就是自注意力机制的全部了,但是对自注意力机制的解析并没有结束,下面从矩阵计算的角度来看自注意力机制。

5.4 自注意力机制中的矩阵计算
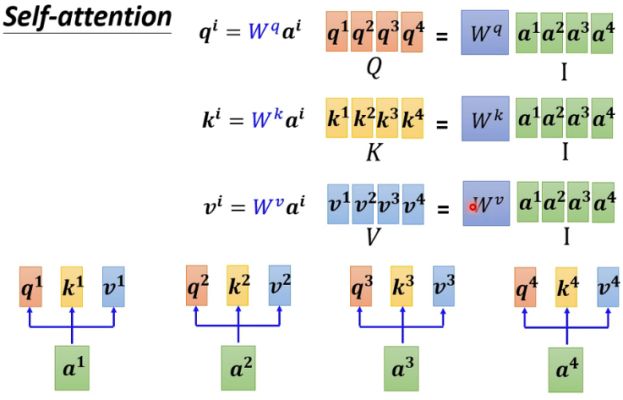
5.4.1 计算矩阵 K 、 V 、 Q K、V、Q K、V、Q
前面提到将 a 1 a^1 a1、 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4分别乘以变换矩阵 W k W^k Wk得到向量 k 1 , k 2 , k 3 , k 4 k^1,k^2,k^3,k^4 k1,k2,k3,k4。我们将输入向量 a 1 a^1 a1、 a 2 a^2 a2、 a 3 a^3 a3、 a 4 a^4 a4拼在一起,得到一个矩阵用 I I I表示,即, I = [ a 1 a 2 a 3 a 4 ] I=[a^1a^2a^3a^4] I=[a1a2a3a4]将key向量 k 1 k^1 k1、 k 2 k^2 k2、 k 3 k^3 k3、 k 4 k^4 k4拼在一起得到一个矩阵用 K K K表示,即, K = [ k 1 k 2 k 3 k 4 ] K=[k^1k^2k^3k^4] K=[k1k2k3k4]用矩阵相乘表示 K K K矩阵的计算过程即, K = W k I K=W^kI K=WkI同理,query向量拼成的矩阵 Q Q Q等于, Q = W q I Q=W^qI Q=WqIvalue向量拼成的矩阵 V V V等于, V = W v I V=W^vI V=WvI。下图展示了上述计算过程。
5.4.2 计算注意力分数矩阵 A ′ A' A′
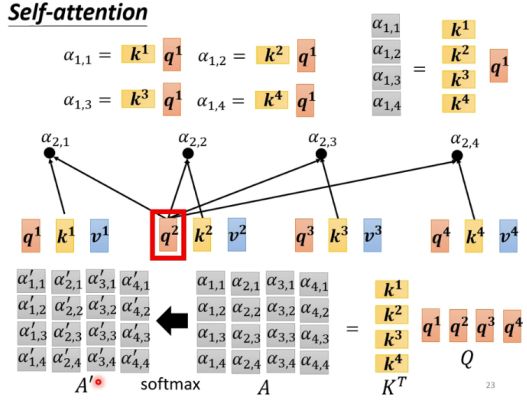
前面提到将 q 1 q^1 q1和四个key向量 k 1 , k 2 , k 3 , k 4 k^1,k^2,k^3,k^4 k1,k2,k3,k4分别做点积,得到四个相关性数值 α 1 , 1 , α 1 , 2 , α 1 , 3 , α 1 , 4 \alpha_{1,1},\alpha_{1,2},\alpha_{1,3},\alpha_{1,4} α1,1,α1,2,α1,3,α1,4。注意这里的向量都是列向量,所以点积可以写成, α 1 , 1 = q 1 ⋅ k 1 = ( k 1 ) T q 1 \alpha_{1,1}=q^1 \cdot k^1 =(k^1)^Tq^1 α1,1=q1⋅k1=(k1)Tq1 α 1 , 2 = q 1 ⋅ k 2 = ( k 2 ) T q 1 \alpha_{1,2}=q^1 \cdot k^2 =(k^2)^Tq^1 α1,2=q1⋅k2=(k2)Tq1 α 1 , 3 = q 1 ⋅ k 3 = ( k 3 ) T q 1 \alpha_{1,3}=q^1 \cdot k^3 =(k^3)^Tq^1 α1,3=q1⋅k3=(k3)Tq1 α 1 , 4 = q 1 ⋅ k 4 = ( k 4 ) T q 1 \alpha_{1,4}=q^1 \cdot k^4 =(k^4)^Tq^1 α1,4=q1⋅k4=(k4)Tq1
用矩阵计算表示上述计算过程为 [ α 1 , 1 α 1 , 2 α 1 , 3 α 1 , 4 ] = [ ( k 1 ) T ( k 2 ) T ( k 3 ) T ( k 4 ) T ] q 1 = K T q 1 \begin{bmatrix}\alpha_{1,1} \\\alpha_{1,2} \\\alpha_{1,3} \\\alpha_{1,4}\end{bmatrix}=\begin{bmatrix}(k^1)^T\\(k^2)^T\\(k^3)^T\\(k^4)^T\end{bmatrix}q^1=K^Tq^1 ⎣⎢⎢⎡α1,1α1,2α1,3α1,4⎦⎥⎥⎤=⎣⎢⎢⎡(k1)T(k2)T(k3)T(k4)T⎦⎥⎥⎤q1=KTq1将 K T K^T KT与 q 2 、 q 3 、 q 4 q^2、q^3、q^4 q2、q3、q4相乘可以得到相似的结果,即, A = [ α 1 , 1 α 2 , 1 α 3 , 1 α 4 , 1 α 1 , 2 α 2 , 2 α 3 , 2 α 4 , 2 α 1 , 3 α 2 , 3 α 3 , 3 α 4 , 3 α 1 , 4 α 2 , 4 α 3 , 4 α 4 , 4 ] = [ ( k 1 ) T ( k 2 ) T ( k 3 ) T ( k 4 ) T ] [ q 1 q 2 q 3 q 4 ] = K T Q A=\begin{bmatrix} \alpha_{1,1}&\alpha_{2,1} &\alpha_{3,1} &\alpha_{4,1} \\ \alpha_{1,2}&\alpha_{2,2} &\alpha_{3,2} &\alpha_{4,2} \\ \alpha_{1,3}&\alpha_{2,3} &\alpha_{3,3} &\alpha_{4,3} \\ \alpha_{1,4}&\alpha_{2,4} &\alpha_{3,4} &\alpha_{4,4} \end{bmatrix}=\begin{bmatrix}(k^1)^T\\(k^2)^T\\(k^3)^T\\(k^4)^T\end{bmatrix}[q^1q^2q^3q^4]=K^TQ A=⎣⎢⎢⎡α1,1α1,2α1,3α1,4α2,1α2,2α2,3α2,4α3,1α3,2α3,3α3,4α4,1α4,2α4,3α4,4⎦⎥⎥⎤=⎣⎢⎢⎡(k1)T(k2)T(k3)T(k4)T⎦⎥⎥⎤[q1q2q3q4]=KTQ A A A矩阵通过softmax层归一化后得到 A ′ A' A′ 。上述计算过程如下图所示。
5.4.3 计算输出矩阵 O O O
前面讲到将向量 v 1 , v 2 , v 3 , v 4 v^1,v^2,v^3,v^4 v1,v2,v3,v4分别乘以对应的注意力分数 α 1 , 1 ′ , α 1 , 2 ′ , α 1 , 3 ′ , α 1 , 4 ′ \alpha^{'}_{1,1},\alpha^{'}_{1,2},\alpha^{'}_{1,3},\alpha^{'}_{1,4} α1,1′,α1,2′,α1,3′,α1,4′,并进行求和,输出向量 b 1 b^1 b1,这个过程用矩阵计算可表示为, b 1 = [ v 1 v 2 v 3 v 4 ] [ α 1 , 1 ′ α 1 , 2 ′ α 1 , 3 ′ α 1 , 4 ′ ] = V [ α 1 , 1 ′ α 1 , 2 ′ α 1 , 3 ′ α 1 , 4 ′ ] b^1=[v^1v^2v^3v^4]\begin{bmatrix}\alpha^{'}_{1,1} \\\alpha^{'}_{1,2} \\\alpha^{'}_{1,3} \\\alpha^{'}_{1,4}\end{bmatrix}=V\begin{bmatrix}\alpha^{'}_{1,1} \\\alpha^{'}_{1,2} \\\alpha^{'}_{1,3} \\\alpha^{'}_{1,4}\end{bmatrix} b1=[v1v2v3v4]⎣⎢⎢⎢⎡α1,1′α1,2′α1,3′α1,4′⎦⎥⎥⎥⎤=V⎣⎢⎢⎢⎡α1,1′α1,2′α1,3′α1,4′⎦⎥⎥⎥⎤
通过相似的计算,也可以得到 b 2 、 b 3 、 b 4 b^2、b^3、b^4 b2、b3、b4,即, O = [ b 1 b 2 b 3 b 4 ] = [ v 1 v 2 v 3 v 4 ] [ α 1 , 1 ′ α 2 , 1 ′ α 3 , 1 ′ α 4 , 1 ′ α 1 , 2 ′ α 2 , 2 ′ α 3 , 2 ′ α 4 , 2 ′ α 1 , 3 ′ α 2 , 3 ′ α 3 , 3 ′ α 4 , 3 ′ α 1 , 4 ′ α 2 , 4 ′ α 3 , 4 ′ α 4 , 4 ′ ] = V A ′ O=[b^1b^2b^3b^4]=[v^1v^2v^3v^4]\begin{bmatrix} \alpha^{'}_{1,1}&\alpha^{'}_{2,1} &\alpha^{'}_{3,1} &\alpha^{'}_{4,1} \\ \alpha^{'}_{1,2}&\alpha^{'}_{2,2} &\alpha^{'}_{3,2} &\alpha^{'}_{4,2} \\ \alpha^{'}_{1,3}&\alpha^{'}_{2,3} &\alpha^{'}_{3,3} &\alpha^{'}_{4,3} \\ \alpha^{'}_{1,4}&\alpha^{'}_{2,4} &\alpha^{'}_{3,4} &\alpha^{'}_{4,4} \end{bmatrix}=VA' O=[b1b2b3b4]=[v1v2v3v4]⎣⎢⎢⎢⎡α1,1′α1,2′α1,3′α1,4′α2,1′α2,2′α2,3′α2,4′α3,1′α3,2′α3,3′α3,4′α4,1′α4,2′α4,3′α4,4′⎦⎥⎥⎥⎤=VA′

5.4.4 自注意力矩阵计算总结
综上,自注意力机制的计算过程可总结为,
(1)计算 Q 、 K 、 V Q、K、V Q、K、V矩阵 Q = W q I Q=W^qI Q=WqI K = W k I K=W^kI K=WkI V = W v I V=W^vI V=WvI
(2)计算注意力分数矩阵 A ′ A' A′ A = K T Q A=K^TQ A=KTQ A ′ = softmax ( A ) A'=\text{softmax}(A) A′=softmax(A)
(3)计算输出矩阵 O O O O = V A ′ O=VA' O=VA′
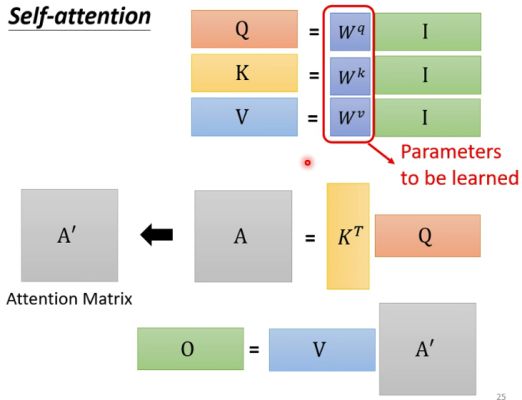
可以看出,自注意力机制看起来比较复杂,其实计算过程并不复杂,需要学习的参数只有 W q 、 W k 、 W v W^q、W^k、W^v Wq、Wk、Wv。
5.5 多头自注意力机制
自注意力机制还有一个进阶版,叫多头自注意力机制(multi-head self-attention)。为什么要多头呢?自注意力机制实质上是用过 q q q向量去找相关的 k k k向量,但是相关性可能有多种,一个 q q q只能找到一种相关的 k k k向量,因此就要引入多个 q q q向量和 k k k向量来捕捉多种相关性。多头自注意力机制很简单,设置多组矩阵 W q , i 、 W k , i 、 W v , i W^{q,i}、W^{k,i}、W^{v,i} Wq,i、Wk,i、Wv,i,每一组 W q , i 、 W k , i 、 W v , i W^{q,i}、W^{k,i}、W^{v,i} Wq,i、Wk,i、Wv,i只进行内部计算,得到相应的输出 O i O^i Oi,如下图所示。

在得到不同的输出 O i O^i Oi后,再将其拼到一起,形成一个大的矩阵。如果是2头,就将这2个输出直接拼到一起。然后通过一个转换矩阵 W o W^o Wo将拼接的矩阵转换成原输出的长度的向量,即, O = W o [ O 1 O 2 ] O=W^o\begin{bmatrix}O^1\\O^2 \end{bmatrix} O=Wo[O1O2]
因此,多头注意力机制要多一个参数矩阵,即 W o W^o Wo。
6.Transformer——实现“序列to序列”的转换
6.1 Transformer 概述
在机器学习中,我们有很多任务都是 “序列to序列” 的形式,比如语音识别、机器翻译、文本标注等等。而且在这些任务中,输入序列和输出序列的长度都是不定的,如么如何实现这种序列的转换呢?这就要用到一个很常见的网络架构— transformer 。transformer的一般结构如下图所示,包括编码(Encoder)和解码(Decoder)两个部分。Encoder对输入序列进行编码输出一个序列,转交给Decoder,Decoder对这个序列进行解码,输出我们需要的序列。

6.2 Transformer的Encoder
首先,我们来看一下transformer的Encoder架构是怎样的。transformer对输入序列进行编码生成另一个长度相等的序列,如下图所示,这里假设输入序列是向量 x 1 、 x 2 、 x 3 、 x 4 x_1、x_2、x_3、x_4 x1、x2、x3、x4,对应的输出是向量 h 1 、 h 2 、 h 3 、 h 4 h_1、h_2、h_3、h_4 h1、h2、h3、h4。编码的目的实际上就要考虑序列的全局并聚焦重点,所以Encoder的核心就是自注意力机制,但不仅仅只有自注意力机制。

Encoder由多个Block组成,每个Block又由自注意力(self-attention)网络和全连接(full-connected)组成。向量 x 1 、 x 2 、 x 3 、 x 4 x_1、x_2、x_3、x_4 x1、x2、x3、x4通过自注意力网络后生成四个向量,这些向量是考虑了序列全局的,然后每个向量再通过一个全连接网络进行一次变换得到四个向量,通过几次Block后才输出向量 h 1 、 h 2 、 h 3 、 h 4 h_1、h_2、h_3、h_4 h1、h2、h3、h4。

实际上,Block的计算还有一些细节,如下图所示。具体包括两个方面:
- x 1 、 x 2 、 x 3 、 x 4 x_1、x_2、x_3、x_4 x1、x2、x3、x4通过自注意力网络后并不是直接输入到全连接层。首先,自注意力网络的输出向量与它的输入向量进行了求和。这种操作在深度网络中很常见,有一个专门的名字叫做残差(residual),残差操作的目的是为了防止梯度消失和网络退化。其次,经过残差操作后,进行了一次Layer normalization,把向量转化成均值为0方差为1的向量,即归一化。计算过程如下图所示(下面这个图有点错误,公式应当是 x i ′ = x i − m σ x'_i=\frac{x_i-m}{\sigma } xi′=σxi−m)。Layer normalization是为了防止向量落在激活函数的饱和区。经过上述两个过程的计算后,才得到全连接层的输入。
- 全连接层的输出也不是直接输出到下一层Block,同样经过了残差和Layer normalization的操作。

总结起来,Encoder的全部计算过程如下图所示,在一个Block中,首先经过一个Multi-Head Attention层,然后进行一次残差(residual)和Layer normalization操作,然后输入到一个全连接层(即Feed Forward),重复多个Block最后输出一个序列。
下面这个图值得注意的一个地方是输入向量并不是直接输入到Encoder,而是叠加了一个位置编码(Positional Encoding)。所谓位置编码是指将序列中某个向量所处的位置进行编码,生成一个与向量长度一样的向量,这对于自然语言处理是很重要的。例如进行此行标注的时候,句首的词是动词的可能性很小。位置编码的方式有很多,现在也有很多文章在研究一些新的方法,感兴趣的可以去研究一下。

6.3 Transformer的Decoder
Encoder对输入进行编码后输出一个序列,Decoder则要根据这个序列输出我们最后想要的一个序列。以语音识别为例,我们对着机器说,“机器学习”。Encoder对我们的语音进行编码生成一个序列,Decoder就是要根据这个序列输出“机器学习”几个字,那么是如何实现的呢?
6.3.1 Decoder的自回归(Autoregressive)机制。
首先,我们要设置一个特殊的符号“Begin”作为输入,Decoder结合Encoder输出的序列和“Begin"这个输入产生一个向量。这个向量的长度非常长,长到和字典的大小相同。假如我们的字典是中文常用词3500字,那么这个向量的长度就是3500。这个向量再经过一个softmax操作,输出一个概率分布,概率最大的那个字就是“Begin”的输出。比如上面这个例子“机”字的概率最大,那么就输出“机”。

输出“机”之后,再将“机”作为Decoder新的输入。这样,Decoder的输入除了“Begin”之外,又多了一个“机”。通过Decoder和softmax之后,又输出一个“器”,然后又将“器”作为新的输入。重复上述过程,周而复始的将新的输出作为新的输入,又输出新的输出。

但是还有一个重要的问题,机器不能这么一直操作下去吧?在何时停止这个循环呢?这就需要在字典中再添加一个特殊的符号“End”。当输出一个“End”时,就停止上述循环,输出完整的序列。这样一个过程就是Decoder的自回归工作机制。那么Decoder的内部结构到底是怎样的呢?

6.3.2 Decoder的结构
Decoder的内部结构如下图所示,可以看出Decoder和Encoder的结构非常相似,但是有些许不同:首先在第一个自注意力层中多了一个"Masked"的字样,其次多了一个自注意力层。

首先,我们来看看第一个自注意力层多出个“Masked"是怎么回事。 前面讲自注意力机制的时候,我们讲输出 b 1 b^1 b1是考虑了输入序列全局的,即考虑了 a 1 、 a 2 、 a 3 、 a 4 a^1、a^2、a^3、a^4 a1、a2、a3、a4所有向量的信息,如下图所示。

但是注意到这里在输出”机“的时候,只能看到"Begin"一个向量,后面的向量是看不到的。对应的,如果我们假设”机“就是 b 1 b^1 b1,那么 b 1 b^1 b1只能利用 a 1 a^1 a1的信息,没法利用 a 2 、 a 3 、 a 4 a^2、a^3、a^4 a2、a3、a4的信息。同理,在输出“器”的时候,只能看到"Begin、机"两个向量,后面的向量也看不到,对应的 b 2 b^2 b2就只能利用 a 1 、 a 2 a^1、a^2 a1、a2的信息。以此类推, b 3 b^3 b3就只能利用 a 1 、 a 2 、 a 3 a^1、a^2、a^3 a1、a2、a3的信息, b 4 b^4 b4能利用 a 1 、 a 2 、 a 3 、 a 4 a^1、a^2、a^3、a^4 a1、a2、a3、a4的信息。

因此,Decoder的第一层自注意力网络多了一个“masked”。所谓“masked”就是盖起来的意思。比如在输出 b 2 b^2 b2时,是要把 a 3 、 a 4 a^3、a^4 a3、a4盖起来的,也就是将 α 2 , 3 ′ 、 α 2 , 4 ′ \alpha^{'}_{2,3}、\alpha^{'}_{2,4} α2,3′、α2,4′设为0即可,如下图所示,

现在我们已经理解了“masked”是怎么回事,接下来再看看多出一个自注意力层是怎么回事。 从下面这个图可以看出,多出来的自注意力层是连接Encoder和Decoder的桥梁,这一层称为“Cross attention”。

Cross attention的工作机制如下图所示,具体过程是:Decoder的输入通过masked self-attention层之后输出一个向量,该向量乘以一个转换矩阵得到一个向量 q q q。Encoder的输出序列乘以转换矩阵分别得到 K K K矩阵和 V V V矩阵,这里的 q q q再与上述 K K K矩阵和 V V V矩阵进行交叉计算得到一个新的向量 v v v。因此,Cross-Attention是利用Encoder自己的输入产生query向量 q q q,然后再去Encoder的输出序列中抽取信息,以作为输出。

7.BERT——自监督学习的典范
7.1 自监督学习的概念
在机器学习中,最常见的是监督学习(Supervised learning)。假设模型的输入是 x x x,输出是 y y y,我们如何使模型输出我们期望的 y y y呢?我们得拥有已标注的(label)的数据,例如图片识别,我们得有一堆的图片,并且这些图片被标注了是什么。然后通过这些已标注的数据对模型进行训练,使模型的输出 y y y尽可能地接近标签 y ′ y' y′,这是监督学习。那么什么是自监督学习呢?假设我们拥有一堆的数据,但是没有标注,我们想办法将这堆数据 x x x分成两个部分,一部分作为模型的输入 x ′ x' x′,一部分作为模型的标签 x ′ ′ x'' x′′。然后对模型进行训练,使模型地输出 y y y尽可能地接近标签 x ′ ′ x'' x′′。注意这里 x ′ ′ x'' x′′不是人标注的,而是数据里本来就有的。这说起来有点抽象,但是通过BERT这个例子就很容易明白了。
![]()
7.2 BERT概述
BERT的全称是Bidirectional Encoder Representation from Transformers,即双向Transformer的Encoder。因此BERT的网络架构和Transformer的Encoder是一样的,关于Transformer的细节请看上一节。因此BERT的任务就是输入一个序列,然后输出一个序列,输出序列和输入序列的长度是一样的。通过Transformer中的自注意力机制,BERT具有考虑序列全局的能力。由于BERT一般用于自然语言处理,所以BERT的输入一般使一排文字,然后输出一组向量,向量的个数和文字的个数是一样的。
7.3 BERT的训练
所谓自监督学习,和监督学习不同的地方就在于训练。BERT的训练方式有两种:Masked Language Model和Next Sentence Prediction。
7.3.1 Masked Language Model
Masked Language Model的工作机制如下图所示,类似于让BERT做完形填空。在训练过程中,随机盖掉句子中的一些字,这些被盖掉的字要么替换成一个特殊符号“MASK”,要么随机替换成其他字。然后将替换后的句子当成BERT的输入,被盖掉的字对应的输出向量通过一个Linear层和softmax操作之后输出一个概率分布。前面讲transformer的时候,讲到了这个概率分布向量的长度和字典的长度是一样的,每个字都有一个对应的概率,概率最大的字就是最后的预测结果。在训练过程中,要使预测输出的字和被盖掉的字尽可能一致。这其实就是一个分类问题,类别的数目和字典的大小一样,损失函数是交叉熵。通过这种简单的方式就实现了自监督学习,它不需要我们去人工标注数据,它的标签来自于数据本身,这是非常巧妙的。
![]()
7.3.2 Next Sentence Prediction
Next Sentence Prediction的工作机制如下图所示。在Next Sentence Prediction的训练任务中,BERT的输入是两个句子加上两个特别的符号“CLS”,“SEP”。其中“CLS”是一个开始符号,“SEP”将两个句子隔开。Next Sentence Prediction的任务是要预测这两个句子是否是相接的,“CLS”输出的向量通过Linear层后输出“yes”和“no”,“yes”表示两个句子是前后相接的,“no”则相反。训练数据的正例是正常的一篇文章中上下连贯的两句话,负例是将正常相接的下一句话随即替换成另外一句话。但是研究表明,这种训练任务对于BERT的训练用处不大。因此BERT的训练主要还是依赖于Masked Language Model。
![]()
7.4 BERT的应用
BERT在自然语言处理领域基本上都可以用上,其应用机制如下图所示,分为预训练(Pre-train) 和微调(Fine-tune) 两个部分。
预训练(Pre-train) 就是指上面所说的Masked Language Model和Next Sentence Prediction两个自监督训练任务。这部分工作实际上由一些搞深度学习的大户做好了,比如google、讯飞等,并不需要我们自己训练,我们只需要将人家训练好的BERT拿来用就行了。
微调(Fine-tune) 是指根据我们的下游任务(如机器翻译、智能问答、文本标注等),再利用下游任务的少量标注数据对下游任务的参数进行微调即可。
![]()
下面以“基于抽取的智能问答(Extraction-based Question Answering)”为例说明BERT的应用机制。“基于抽取的智能问答”类似于阅读理解,让机器读一段文字,然后提出几个问题,机器从阅读到的文字中抽取答案。对于该任务,模型的输入就是文章和问题,输出是两个整数值“ s s s”和“ e e e”。“ s s s”代表答案在文章中的起始位置,“ e e e”代表答案在文章中的结束位置。例如下图中第一个问题的答案是“gravity”,而“gravity”位于文章的第17个字符(不含标点),因此模型的输出“ s = 17 s=17 s=17”,“ e = 17 e=17 e=17”。同理,第三个问题的答案是“within a cloud”,而它们位于第77-79个字符,因此模型的输出“ s = 77 s=77 s=77”,“ e = 79 e=79 e=79”。
![]()
处理上述这个问题的做法如下图所示,模型的输入是问题和文章,问题和文章通过符号“SEP”隔开。然后随机初始化两个向量(图中的橘黄色向量和蓝色向量),向量的长度和BERT输出向量的长度一样,然后将这两个向量分别去和文章输出的向量做点积,然后通过Softmax输出概率分布,概率最大的分别是答案的起始位置和结束位置。这个任务中训练的参数只有随机初始化的两个向量,BERT中的参数都不需要训练的。
![]()
可以看出利用BERT的预训练,做下游任务时就很简单了,训练的参数也非常少,而且实践证明这样做的效果是非常好的,超过了传统的一些做法。这就是BERT的魅力所在。
8.生成对抗网络(Generative Adversarial Networks,GAN)——让机器学习具有创造力
8.1生成对抗网络概述
有时候我们希望网络具有一定的创造力,比如画画、编曲等等,能否实现呢?是可以实现的,大家可以鉴别一下下面这几张照片,哪些是真实的人脸,哪些是机器生成的人脸。很难判断吧?本节最后会给出答案。
![]()
要实现上述能力,就要用到一种新的网络架构— 生成对抗网络(Generative Adversarial Net,GAN
) 。首先,我们大概来了解一下什么是 “生成” ,什么是 “对抗”。
8.1.1 对“生成”的理解
假设我们设计一个网络,将其称为 “生成器(Generator)”。生成器的输入是一个向量 z z z,该向量一般是低维向量,它是通过一个特定的分布采样出来的,例如正态分布。生成器的输出是另一个向量 y y y,该向量是一个高维向量,比如一个二次元的人脸。由于生成器的输入向量是通过一个分布随机采样的,所以输入向量每次都是不一样的,因此生成器每次的输出也是不一样的,会形成一个复杂的分布。尽管输出向量不一样,但是我们要求这些输出向量都是二次元的人脸,而不是其它。也就是说期望生成器输出的复杂分布要和某个特定分布(例如所有二次元人脸的集合)尽可能相似,如何做到呢?这就要用到“对抗”。
![]()
8.1.2 对“对抗”的理解
我们常说要“感谢对手”,为什么呢?因为对手逼得我们不断想办法进步,最后让我们进化成长为优秀的人。为了使生成网络不断进化以成为画画高手,我们还需要训练另外一个网络,叫做 “鉴别器(Discriminator)” 。鉴别器是专门用来和生成网络进行对抗的,就是用它来逼得生成网络不断进化。鉴别器的输入是一张图片,它的输出则是一个0-1的数字,数字越大就越认为这张图片是一个二次元图片,数字越小呢就越认为这张图片不是一个二次元图片。比如下图中上面两张图片很清楚是二次元,所以鉴别器输出1.0,而下面两张图片很模糊,所以鉴别器输出0.1。因此,简单点讲,鉴别器的功能就是判断某张图片到底是不是二次元图片。
![]()
现在我们把这个鉴别器拿过来和生成器进行对抗:
- ①版本1的生成器的参数是随机生成的,所以其生成的图片啥都不是。这 时候,我们对鉴别器进行训练,以使鉴别器能够鉴别出哪些是生成器生成的图片,哪些是真实的二次元人脸。经过训练后,我们得到了版本1的鉴别器。
- ②在版本1的鉴别器的基础上,我们再来训练生成器,训练的目的是让鉴别器分辨不出哪些是生成器生成的图片,哪些是真实的二次元人脸。通过训练之后,得到了版本2的生成器,此时生成的图片有一点点像二次元了,足以骗过版本1的鉴别器。
- ③在版本2的生成器的基础上,我们接着训练鉴别器,同样是要使鉴别器能够鉴别出哪些是版本2生成器生成的图片,哪些是真实的二次元人脸。通过训练之后,得到了版本2的鉴别器。
- ④重复上述过程,不断进化生成器和鉴别器,最后生成器可以生成非常逼真的二次元人脸。
通过上述过程我们可以看出,生成器和鉴别器在不断的对抗过程中,两者都在不断的进步,可以说是对抗成就了对方。所以,它们亦敌亦友,相爱相杀,既对立又统一。
![]()
8.2 生成对抗网络的理论基础
我们刚才提到生成器的输入是由一个简单的分布(如正态分布)采样得到的一堆向量,输出是一堆向量构成另一个一个复杂的分布,用 P G P_G PG表示。我们期望 P G P_G PG和某个特定的分布尽可能地相似,而这个分布来自于一堆真实的数据,这个分布表示为 P d a t a P_{data} Pdata。如果我们用 D i v ( P G , P d a t a ) Div(P_G,P_{data}) Div(PG,Pdata)来表示这两个分布的Divergence(这个英文不好翻译,暂且理解为“差异程度”吧),那么我们的目标就是寻找一个生成器 G ∗ G^* G∗要使 D i v ( P G , P d a t a ) Div(P_G,P_{data}) Div(PG,Pdata)最小,即, G ∗ = a r g min G D i v ( P G , P d a t a ) G^*=arg\min_{G} Div(P_G,P_{data}) G∗=argGminDiv(PG,Pdata)我们知道在机器学习中,训练的目标是要使损失函数最小,所以在该任务中损失函数就是 D i v ( P G , P d a t a ) Div(P_G,P_{data}) Div(PG,Pdata)。但是有一个很关键的问题,我们如何计算这两个分布的Divergence呢?好像没法用解析式去描述这两个分布的Divergence,那怎么办呢?我们可以通过采样的方式来计算这两个分布的Divergence。
![]()
采样是很好办的,以二次元人脸生成器为例。 P d a t a P_{data} Pdata的采样很简单,我们从一堆二次元的图库中随机采样一些图片就行了。 P G P_{G} PG的采样也很简单,我们从正态分布中采样一些向量,生成器输出一些图片,就得到 P G P_{G} PG的采样图片了。我们有了 P d a t a P_{data} Pdata和 P G P_{G} PG的采样了,那么怎么计算 D i v ( P G , P d a t a ) Div(P_G,P_{data}) Div(PG,Pdata)呢?这就需要用到鉴别器了。
![]()
假设从 P d a t a P_{data} Pdata采样得到的数据用蓝色五角星表示,从 P G P_{G} PG采样得到的数据用黄色五角星表示。鉴别器的目的就是遇到蓝色五角星时输出的分数要尽量高,遇到黄色五角星时输出的分数要尽量低。如果用 V ( D , G ) V(D,G) V(D,G)鉴别器训练的目标函数(最大化一般称为目标函数,最小化一般称为损失函数),那么就有, V ( G , D ) = E y ∼ P data [ log D ( y ) ] + E y ∼ P G [ log ( 1 − D ( y ) ) ] V(G, D)=E_{y \sim P_{\text {data }}}[\log D(y)]+E_{y \sim P_{G}}[\log (1-D(y))] V(G,D)=Ey∼Pdata [logD(y)]+Ey∼PG[log(1−D(y))]其中 E y ∼ P data [ log D ( y ) ] E_{y \sim P_{\text {data }}}[\log D(y)] Ey∼Pdata [logD(y)]表示当 y y y从 P d a t a P_{data} Pdata中采样,通过鉴别器后的输出 D ( y ) D(y) D(y)要尽可能大, E y ∼ P G [ log ( 1 − D ( y ) ) ] E_{y \sim P_{G}}[\log (1-D(y))] Ey∼PG[log(1−D(y))]表示当 y y y从 P d a t a P_{data} Pdata中采样,通过鉴别器后的输出 D ( y ) D(y) D(y)要尽可能小,因此加了个负号。可以看出该式中还专门取了个对数,这是为了和分类问题中的交叉熵保持一致,因为该式加个负号就是分类问题中的交叉熵了。在训练分类器的时候是要最小化交叉熵,这里要最大化 V ( D , G ) V(D,G) V(D,G),所以两者是等同的。因此,鉴别器也可以看成一个二分类器,一类数据从 P d a t a P_{data} Pdata采样得到,一类数据 P G P_{G} PG采样得到。
最重要的一点是, max D V ( D , G ) \max_{D}V(D,G) maxDV(D,G)和上面提到的Divergence是相关的,这一点在GAN最原始的文章中有严格的数学推理。
![]()
我们可以从直观上来理解为什么 max D V ( D , G ) \max_{D}V(D,G) maxDV(D,G)和 D i v ( P G , P d a t a ) Div(P_G,P_{data}) Div(PG,Pdata)是相关的。假设 D i v ( P G , P d a t a ) Div(P_G,P_{data}) Div(PG,Pdata)比较小,表示这两者很相似,那么从 P G P_{G} PG和 P d a t a P_{data} Pdata采样得到的数据混到一起就很难被鉴别,因此鉴别器的 max D V ( D , G ) \max_{D}V(D,G) maxDV(D,G)就不会太大;相反地,如果 D i v ( P G , P d a t a ) Div(P_G,P_{data}) Div(PG,Pdata)比较大,表示这两者差异性很大,那么从 P G P_{G} PG和 P d a t a P_{data} Pdata采样得到的数据混到一起就比较容易被鉴别,因此鉴别器的 max D V ( D , G ) \max_{D}V(D,G) maxDV(D,G)就会比较大。希望了解详情的,请移步GAN的原文。
![]()
既然我们已经知道 max D V ( D , G ) \max_{D}V(D,G) maxDV(D,G)和 D i v ( P G , P d a t a ) Div(P_G,P_{data}) Div(PG,Pdata)是相关的,而且是正相关的。所以生成器的损失函数中的 D i v ( P G , P d a t a ) Div(P_G,P_{data}) Div(PG,Pdata)就可以用 max D V ( D , G ) \max_{D}V(D,G) maxDV(D,G)来进行替换,可以得到, G ∗ = a r g min G max D V ( D , G ) G^*=arg\min_{G} \max_{D}V(D,G) G∗=argGminDmaxV(D,G)这个损失函数有点复杂,又是 min \min min,又是 max \max max。其实这个损失函数包含了两个优化问题:首先是在固定生成器 G G G的情况下,找到一个鉴别器 G G G使 V ( D , G ) V(D,G) V(D,G)最大,然后是要找到鉴别器 G G G,使 max D V ( D , G ) \max_{D}V(D,G) maxDV(D,G)最小。因此,前面提到的对抗过程就是求解 G ∗ = a r g min G max D V ( D , G ) G^*=arg\min_{G} \max_{D}V(D,G) G∗=argminGmaxDV(D,G)的过程。所以生成对抗网络的训练如下图所示。
![]()
对了,本节最前面的人脸全部是由机器生成的,惊叹吧!?
9.领域自适应(Domain adaption)——实现模型的自适应迁移
9.1领域自适应网络概述
有时候我们在某个领域训练出的一个模型,想迁移到另一个领域,这样我们就不需要每个领域都去标注大量的数据了。但是这两个领域的数据分布是有些差异,要如何办呢?比如我们在黑白图片上训练出了数字的识别模型,但是我们希望该模型用到彩色数字的识别上。如果直接将模型迁移过去,结果并不理想,在黑白图片上的测试准确率可以达到99.5%,但迁移到彩色图片上时测试准确率仅57.5%。这是由于黑白图片和彩色图片的分布不一样,那么如何处理这种情况呢?我们需要用到 “领域自适应(Domain Adaption)”。
![]()
9.2 领域自适应的基本思路
我们将有标签的、能够训练模型的领域称为源域(Source Domain),无标签或者只有少量标签的领域称为目标域(Target Domain),我们的目的是要将源域训练得到的模型迁移到目标域。但是源域数据和目标域数据的分布不一样,领域自适应的基本思路是设计一个特征提取器,使得从源域和目标域提取的特征分布是一样的,如下图所示。
![]()
我们将数字识别任务分成特征提取器和标签预测器两个部分,特征提取器有若干层网络负责提取图片的特征,并输出一个向量,然后将这个向量交给标签预测器,标签预测器也有若干层,负责根据特征提取输出的向量预测图片所展示的数字。现在有一堆的源域数据,它们是有标签的,还有一堆目标域数据,它们是没有标签的。假设源域数据输入到特征提取器输出的结果是蓝色的点,而目标域数据输入到特征提取器输出的结果是红色的点。我们要训练这个特征提取器,尽可能地使蓝色的点和红色地点混在一起分不出差异。那么要如何训练这个特征提取器呢?
![]()
9.3 域分类器的引入
除了上述的特征提取器和标签预测器外,我们再引入一个新的网络,叫做 “域分类器”。域分类器的任务就是负责鉴别特征提取器输出的特征是来自源域数据还是目标域数据。而特征提取器要尽量减小源域数据数据和目标域数据输出向量的差异,以骗过域分类器,使其无法正确的鉴别。说到这里,大家应该想到了前面的生成对抗网络(GAN),这两者确实很像。这里的特征提取器就相当于GAN的生成器,而这里的域分类器就相当于GAN的鉴别器。那么有一个问题,特征提取器似乎明显要占优势,比如一个极端的情况,特征提取器无论是何输入都输出0,那么鉴别器无论如何也无法鉴别出哪些来自源域,哪些来自目标域。但是这种情况其实是不会出现的。因为预测器也需要特征提取器输出的这个向量,用来判断图片的标签是什么。如果特征提取器无论输入是什么都输出0的话,那么预测器是无法根据这个向量来预测图片标签的。
![]()
下面再利用数学符号把上述过程再理一下。首先,我们假设三个网络的参数分别为:特征提取器—— θ f \theta_f θf,标签预测器—— θ p \theta_p θp,域分类器—— θ d \theta_d θd。由于源域数据是有标签的,因此可以算出标签预测器的输出和源域数据标签之间的交叉熵,根据这个交叉熵可以定义一个Loss,设为 L L L。训练标签预测器的目标就是要最小化这个 L L L,即 θ p ∗ = min θ p L \theta_{p}^{*}=\min _{\theta_{p}} L θp∗=θpminL。域分类器实际上是一个二分类器,它的任务是区分特征是来自源域还是目标域,这个分类任务也可以定义一个Loss,设为 L d L_d Ld。训练域分类器的目标就是要使这个 L d L_d Ld最小化,即 θ d ∗ = min θ d L d \theta_{d}^{*}=\min _{\theta_{d}} L_{d} θd∗=θdminLd训练特征提取器的目标:一方面要使标签预测器尽量能正确预测出图片标签,即最小化 L L L;另一方面又要尽量骗过域分类器,使其不能正确鉴别,即要最大化 L d L_d Ld,也就是最小化 − L d -L_d −Ld。因此可表示为
θ f ∗ = min θ f L − L d \theta_{f}^{*}=\min _{\theta_{f}} L-L_{d} θf∗=θfminL−Ld
10.强化学习(Reinforcement Learning, RL)——让AlphaGo进化得比人类更强
10.1 题外话:人类棋手的最后赞礼
2016年3月15日,AlphaGo以4:1的比分击败了人类的传奇棋手李世石。在李世石折戟沉沙的当晚,一个名叫柯洁的中国少年站出来说,“就算AlphaGo战胜了李世石,但是它赢不了我”。当时柯洁柯洁是有这个底气的,因为他在世界排行榜上占据第一,曾在正式比赛中以8:2的比分碾压李世石。但是AlphaGo经过9个多月的自我对弈和迭代,AlphaGo已经从对战李世石的V18进化到到V21了,它有了一个新的名字“AlphaGo Zero”。2017年5月,人类第一高手柯洁和“AlphaGo Zero”开启了一段旷世对决。在这段对决中,无论柯洁如何努力,始终脱离不了在“AlphaGo Zero”面前全面落败的结局,期间抑制不住情绪失声痛苦。那么,AlphaGo Zero背后的技术是什么?是如何让它进化得比人类更强的?其实就是强化学习(Reinforcement Learning, RL) 。
10.2 强化学习概述
前面讲到的所有深度学习都是有监督的学习,也就是数据都是有标签的。我们需要告诉机器一个输入应当要有什么样的输出。即使是自监督学习,也是有标签的,只是标签不是人工标注的,而是来自于数据本身。但是在有些任务中,对应一个输出,我们人类也不知道最佳的输出是什么。比如说下围棋,对方落子后,我方的最佳落子在哪儿,恐怕最厉害的棋手也不知道。当然,我们可以通过监督学习的方法,让机器学习许多棋谱,也能使机器称为高手,但是最高水平永远不会超过人类。如果我们希望机器学习获得人类棋谱之外的招数,在与人类对决时候可以出现神之一手,以打败人类最高选手,那么就要用到强化学习了。
10.2.1 强化学习的目标也是要找一个Function
强化学习和一般深度学习的目的是一样的,都是要找一个Function。强化学习要找的Function如下图所示,这个Function我们将其称为Actor。Actor的输入是它对环境的观察,输出是一个行为Action。当Actor输出一个行为后,环境的状态会发生改变,因此Actor又能观察到新的环境,相应的又输出一个新的行为。在Actor和环境互动的过程中,环境会不断地反馈Reward。我们要找到一个Actor(Function),使total reward最大化。

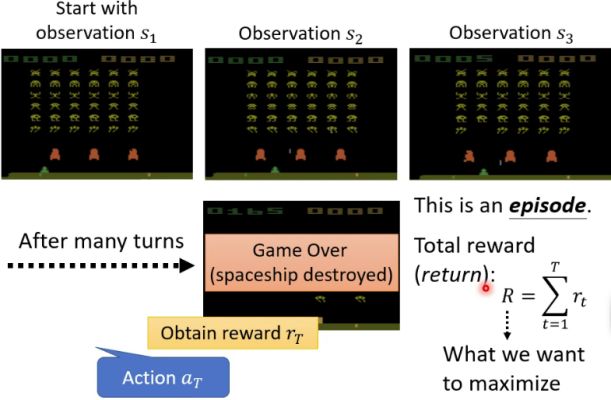
比如训练一个下围棋的Actor。Actor就是AlphaGo,环境就是和AlphaGo对战的人类。Actor的输入是棋盘及棋盘上的双方落子,输出就是下一步落子的位置。Actor每下一个棋子,人类也会下一个棋子,这样Actor观察到的棋盘及棋盘上的双方落子就发生了变化,Actor根据它观察到的新的状态又要输出一个新的落子位置。在这对弈过程中,大部分时间的reward都是0,只有等棋局结束后,才会反馈一个reward,如果是赢了,reward=1,如果输了,reward=0。

10.2.2 强化学习的三个基本步骤
强化学习和一般的深度学习一样也包含定义一个function、定义一个损失函数、优化参数这三个步骤。由于下围棋的模型过于复杂,下面以Space invader的游戏来说明这三个步骤,到本节最后再简单地讲一下AlphaGo的强化学习。
Space invader游戏的规则如下:游戏下端的绿色块是我们的太空船,动作有左移、右移和开火。上面的黄色图标是外星人,我们的目标是要杀掉这些外星人,只要开火集中外星人就可以把它杀掉。中间的橘黄色块是我们防护罩,可以阻挡外星人的进攻,不小心开火打中防护罩会使防护罩变小。我们每击中一个外星人,就可以得到一个分数,也就是reward。游戏的终点是所有外星人被杀掉,或者我们的太空船被摧毁。

10.2.2.1 定义一个function
我们设计一个神经网络模型,输入是游戏画面,输出是左移、右移或者开火的开率。这其实就是一个分类任务,即输入一张图片,输出三个类别的分数。因此,该网络可以使用常见的CNN,当然也可以设计成其他形式的网络架构。但是Actor的时候,可能不会直接采用概率(分数)最大的动作,而是使用采样的方式,从这个概率分布中去采样一个动作。这样做的好处是,机器看到同一个游戏画面,可能会采取不同的行为,这种随机性在RL中很常见。

10.2.2.2 定义一个损失函数
前面提到了,Actor在和环境互动的过程中,环境会不断反馈reward。比如在Space invader游戏中,Actor观察到的环境 s 1 s_1 s1,此时Actor执行的动作是右移,获得的reward是0;然后环境状态变成 s 2 s_2 s2,Actor观察到此状态后执行的动作是开火,获得的reward是5;环境状态变成 s 3 s_3 s3。假设Actor在和环境互动的互动经过了若干轮后,太空船被摧毁,游戏结束,这时候就会获得游戏最后的得分,我们把这样一局游戏称为一个episode。在一个episode中,Actor和环境互动执行了许多Action,每一个Action我们用 a T a_T aT表示,针对每一个Action环境都会反馈一个reward,我们用 r T r_T rT。当一个episode结束后,我们得到了游戏最后的得分,称为Total reward R R R,即 R = ∑ t = 1 T r T R=\sum_{t=1}^T{r_T} R=∑t=1TrT。我们的目标是要最大化 R R R,因此Loss函数即可以定义为负的 R R R。
10.2.2.3 优化参数
在Actor和环境互动中会产生一系列的action和环境状态,我们把这些action和环境状态构成的序列称之为Trajectory,表示为 τ = { s 1 , a 1 , s 2 , a 2 , . . . } \tau=\{s_1,a_1,s_2,a_2,...\} τ={s1,a1,s2,a2,...}。其中actor是一个网络,包含未知参数,我们的目标使要训练出一组参数,使Total reward R R R最大。但是由于环境状态的变化和Reward是黑箱,且一般具有随机性,我们是没办法用一般网络的训练方法的。因此,强化学习最大的挑战就在于参数优化。

10.3 Policy Gradient
10.3.1 Actor的行为控制
对于一个Actor我们如何控制它的行为呢?前面提到了Actor的网络实际上就是一个分类网络,例如Space invader游戏就是读入当前环境的图片输出左移、右移、开火三个类别的概率。因此,我们可以定义一个交叉熵 e t e_t et来评估在环境状态 s t s_t st下网络的输出与合理的动作 a ^ t \hat{a}_t a^t之间的距离。例如在某一环境下合理的动作是左移,而Actor网络的输出是(左移,0.6)、(右移,0.3)、(开火,0.1),那么交叉熵是 e = − ln ( 0.6 ) ≈ 0.51 e=-\ln (0.6) \approx 0.51 e=−ln(0.6)≈0.51。一把游戏结束后,我们计算出许多交叉熵,将它们累加起来,定义一个损失函数: L = ∑ e t L=\sum{e_t} L=∑et。在训练过程中最小化这个 L L L,就可以控制Actor的行为,使其更加合理的执行任务。
更进一步,在某一特定环境 s t s_t st下,Actor执行某个动作 a ^ t \hat{a}_t a^t不只是合理和不合理,而是一个合理的程度,我们用一个分数 A t A_t At来表示。这个 A t A_t At叫做优势函数(Advantage Function),它反映了Actor在某个状态下 s t s_t st下选取某个具体动作 s t s_t st的合理性。
例如,在Space invader游戏中,如果在一个游戏界面中,给Actor的右移打了一个很高的正分数,那么就意味着Actor在当前环境下执行右移这个动作是非常合理的,我们鼓励它这么做;如果在一个游戏界面中,给Actor的左移打了一个很低的负分数,那么就意味着Actor在当前环境下尽量不要执行左移这个动作是很不合理的,我们不期望它这么做。此时,损失函数就为 L = ∑ e t A t L=\sum{e_t}A_t L=∑etAt,即损失函数的每一项在 e t e_t et的基础上再乘了一个 A t A_t At。为了训练Actor,我们需要收集一堆数据,是关于不同环境下Actor执行不同动作的合理程度的,如下图所示的Training Data。这里有一个关键问题,如何去确定这些 A t A_t At呢?如果都是人工确定的,那以上跟传统的监督学习没有任何区别了。我们有没有其他方法确定 A t A_t At呢?

10.3.2 优势函数 A t A_t At的确定
一个最简单的方式是让 A t = r t A_t=r_t At=rt,这里的 r t r_t rt是前面提到的reward。在Space invader游戏中 r t r_t rt就是在某一特定游戏界面 s t s_t st下,Actor执行某个动作 a t a_t at的所获得的分数,如果这个动作是左移或者右移,则 r t = 0 r_t=0 rt=0,如果是开火正好打中了外星人,则 r t = 5 r_t=5 rt=5。但是这样做实际上是一个短视的行为,它只顾了眼前,没有考虑到当前的行为对未来的影响。如果这样设置A,可能会导致Actor一直开火,毕竟只有开火才能获得reward。有很多时候,牺牲当前的利益可能会获得更多的回报。例如在Space invader游戏中,Actor采取右移策略虽然本轮动作不会得分,但是可能有利于后续连续得分。所以,我们需要让Actor看得更远。
那么更好的办法是让 A t = ∑ n = t N r n A_t=\sum_{n=t}^N{r_n} At=∑n=tNrn,即把Actor在环境 s t s_t st下执行动作 a t a_t at后所获得的累积reward作为 A t A_t At。这样,Actor在某一游戏界面下就有可能选择右移,即使没有获得分数,但是有利于后面获得更丰厚的分数。但是,这里还有一个问题,Actor在某一游戏界面下选择右移,可能只对后面几步的分数获得有影响,对再后面的分数获得就影响不大了。举个例子,把Actor最后一次开火获得的分数 r N r_N rN归功于Actor第一个动作 a 1 a_1 a1显然是不太合适的。因此,引入一个大于0小于1的折扣因子 γ \gamma γ,让 A t = ∑ n = t N γ n − t r n A_t=\sum_{n=t}^N{\gamma^{n-t} r_n} At=∑n=tNγn−trn。某个分数离动作 a t a_t at越远, a t a_t at对该分数的贡献就越小,给该分数的权值就越小,这就更合理了。

仍然有一个问题,某个动作的好与坏是相对的,我们希望好的动作尽可能是正的分数,不好的动作尽可能是负的分数,但是在Space invader游戏中并未设置负的reward。因此,设置一个基准 b b b,我们让 A t = ∑ n = t N γ n − t r n − b A_t=\sum_{n=t}^N{\gamma^{n-t} r_n}-b At=n=t∑Nγn−trn−b这样 A A A就会有正有负了。但是一个重要的问题是如何确定这个 b b b呢?这就用到Actor-Critic算法了,后面将介绍。

10.3.3 参数更新算法
Policy Gradient更新参数的算法如下图所示。首先,随机初始化Actor网络的参数 θ 0 \theta^0 θ0。然后进入参数更新的循环,在循环里面:首先,让Actor与环境进行互动,并把互动的过程记录下来,获得一堆的数据 { s 1 , a 1 } , { s 1 , a 1 } , . . . , { s N , a N } \{s_1,a_1\},\{s_1,a_1\},..., \{s_N,a_N \} {s1,a1},{s1,a1},...,{sN,aN} ;然后,根据互动产生的reward计算 A 1 , A 2 , . . . , A N A_1,A_2,...,A_N A1,A2,...,AN ,用于评Actor在特定环境状态下选取某个具体动作的合理性;然后,计算Loss L L L;最后,利用梯度下降更新一次参数。
以上要特别注意到,每更新一次参数都要用新的actor去和环境互动获得新的互动数据,然后再更新参数。对于一般机器学习,数据的收集往往在迭代循环的外面,也就是只需要收集一次数据就行了。但是在这里,每更新一次参数都要重新收集数据。这是因为我们没更新一次参数,Actor的能力就强了一些,此时我们需要用新的Actor去和环境互动才能获得更有价值的数据,这时候的数据对于提升新的Actor的能力才更有帮助。举个例子,刚开始Actor V0是一个Space invader游戏小白,左移、右移和开火都是随机的,差不多得5分就挂了。但是,当Actor迭代了很20代后,Actor V20打Space invader游戏差不多得100分才挂。如果这时候我们还拿刚开始的Actor V0打游戏的数据来训练Actor V20显然是不合适的。所以,我们需要拿Actor V20去打游戏获得的数据再来更新Actor V20。Policy Gradient每次更新参数都要重新收集一次数据,因此训练速度是非常慢的。

10.4 Actor-Critic 算法
10.4.1 价值函数的概念
Actor-Critic 算法除了Actor一个网络之外,还要引入另一个网络,叫Critic。Critic用来评估特定Actor θ \theta θ在某一特定环境状态 s s s下,接下来还可以获得多少回报。当然Critic也有其他变种,比如评估特定Actor θ \theta θ在某一特定环境状态 s s s下并执行了某个动作 a a a后,接下来还可以获得多少回报。这里只介绍第一种情况,我们将其称为价值函数(Value Function),用 V θ ( s ) V^\theta(s) Vθ(s)表示。它的工作是要估计Actor θ \theta θ在某一特定环境状态 s s s下可以获得的折扣累积回报(Discount cumulated reward)。折扣累积回报即 ∑ n = t N γ n − t r n \sum_{n=t}^N{\gamma^{n-t} r_n} ∑n=tNγn−trn。
因此,价值函数是作为一个网络,它的输入是某个环境状态,输出是这个Actor在该环境状态下可以获得的折扣累积回报。例如在Space invader游戏中,价值函数的输入就是某一个游戏界面,输出就是Actor还可以获得多少折扣累积回报。当游戏刚开局的时候,Actor还有很多机会得分,价值函数的输出会比较大;到了游戏快结束时,外星人所剩无几,Actor得分的机会不多了,价值函数的输出会比较小。当Actor打完一局游戏后,每一个游戏界面下的Actor的折扣累积回报都是可以算出来的,而价值函数希望可以做到未卜先知,提前预估Actor可以获得的折扣累积回报。注意到 V θ ( s ) V^\theta(s) Vθ(s)有一个上标 θ \theta θ,因此价值函数的输出是和Actor相关的,即使同一个价值函数,不同的Actor,估计出来的折扣累积回报是不一样的。
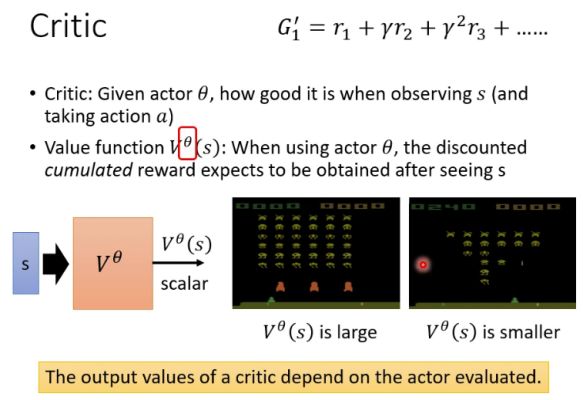
10.4.2 价值函数 V θ ( s ) V^\theta(s) Vθ(s)的训练方法
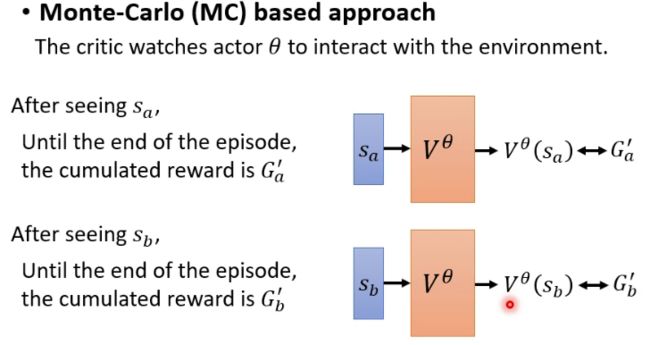
10.4.2.1 基于蒙特卡洛(MC)的方法
基于蒙特卡洛(MC)的方法非常直观。在Actor和环境互动的过程中,把所有回报都记录下来,直到一个episode结束,我们就能计算出每一个环境状态下Actor所获得的折扣累积回报。我们训练价值函数 V θ ( s ) V^\theta(s) Vθ(s)的目标就是让其输出和计算得到的折扣累积回报尽量相等。例如,在环境状态 s a s_a sa下,计算得到折扣累积回报为 G a ′ G'_a Ga′,那么就让 V θ ( s a ) V^\theta(s_a) Vθ(sa)的输出尽可能接近 G a ′ G'_a Ga′即可。我们可以用MAE或者MSE来定义一个LOSS。
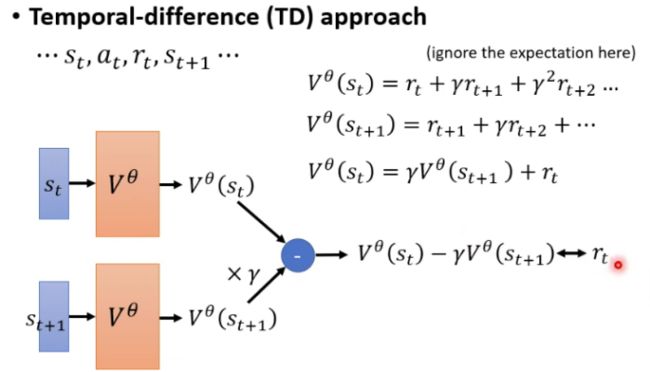
10.4.2.2 基于时序差分(TD)的方法
如果忽略掉 V θ ( s t ) V^\theta(s_t) Vθ(st)的输出和真实 G t ′ G'_t Gt′之间的误差,假设, V θ ( s t ) = ∑ n = t N γ n − t r n V^\theta(s_t)=\sum_{n=t}^N{\gamma^{n-t} r_n} Vθ(st)=n=t∑Nγn−trn则有 V θ ( s t + 1 ) = ∑ n = t + 1 N γ n − t − 1 r n V^\theta(s_{t+1})=\sum_{n=t+1}^N{\gamma^{n-t-1} r_n} Vθ(st+1)=n=t+1∑Nγn−t−1rn
因此就有 V θ ( s t ) = γ V θ ( s t + 1 ) + r t V^\theta(s_{t})=\gamma V^\theta(s_{t+1})+r_t Vθ(st)=γVθ(st+1)+rt
所以一个新的想法是让 V θ ( s t ) − γ V θ ( s t + 1 ) V^\theta(s_{t})-\gamma V^\theta(s_{t+1}) Vθ(st)−γVθ(st+1)尽可能地接近 r t r_t rt就行了,这就是TD的方法。
10.4.3 价值函数 V θ ( s ) V^\theta(s) Vθ(s)在优势函数上的应用
前面提到在设计优势函 A A A的时候,为了使 A A A有正有负,所以我们设置了一个基准 b b b,令 A t = ∑ n = t N γ n − t r n − b A_t=\sum_{n=t}^N{\gamma^{n-t} r_n}-b At=n=t∑Nγn−trn−b
但是有一个很关键的问题使如何去设置这个基准 b b b。其实,可以令 b b b等于价值函数 V θ ( s ) V^\theta(s) Vθ(s),即 A t = ∑ n = t N γ n − t r n − V θ ( s ) A_t=\sum_{n=t}^N{\gamma^{n-t} r_n}-V^\theta(s) At=n=t∑Nγn−trn−Vθ(s)
为什么可以这么做呢?由于Actor的行为具有随机性,因此价值函数的输出其实使对折扣累积回报一种期望,也就是代表了折扣累积回报的一个平均值。如果Actor在环境状态 s t s_t st下,执行了一个动作 a t a_t at所获得的折扣累积回报 ∑ n = t N γ n − t r n \sum_{n=t}^N{\gamma^{n-t} r_n} ∑n=tNγn−trn大于平均折扣累计回报,优势函数 A t A_t At是一个正数,说明动作 a t a_t at是相对合理的;相反的,如果所获得的折扣累积回报小于平均折扣累计回报,优势函数 A t A_t At是一个负数,说明动作 a t a_t at是不太合理。但是该公式还有一个问题,Actor在环境状态 s t s_t st下,执行了一个动作 a t a_t at所获得的回报是 r t r_t rt,这是确定的,但是后续的回报仍然是随机的,所以后续的折扣累计回报应当也要用平均值。Actor在环境状态 s t s_t st下,执行了一个动作 a t a_t at后环境状态变成 s t + 1 s_{t+1} st+1,因此后续的折扣累计回报的平均值就是 V θ ( s + 1 ) V^\theta(s+1) Vθ(s+1)。所以,如果忽略掉价值函数的输出和真实折扣累计回报之间的误差,有 ∑ n = t N γ n − t r n = r t + V θ ( s + 1 ) \sum_{n=t}^N{\gamma^{n-t} r_n}=r_t+V^\theta(s+1) n=t∑Nγn−trn=rt+Vθ(s+1)因此, A t A_t At可以表示为, A t = V θ ( s + 1 ) + r t − V θ ( s ) A_t=V^\theta(s+1)+r_t-V^\theta(s) At=Vθ(s+1)+rt−Vθ(s)这就是大名鼎鼎的Actor-Critic算法了。

11.元学习(Meta-learning)——让机器学习如何学习
11.1 元学习概述
元学习的意思即**“学会如何学习”** 。 在机器学习中,工作量最大也是最无聊的事情就是调参。我们针对每一个任务从头开始进行这种无聊的调参,然后耗费大量的时间去训练并测试效果。因此,一个直观的想法是:我们是否能让机器自己学会调参,在遇到相似任务时能够触类旁通、举一反三,用不着我们从头开始调参,也用不着大量标签数据重新进行训练。
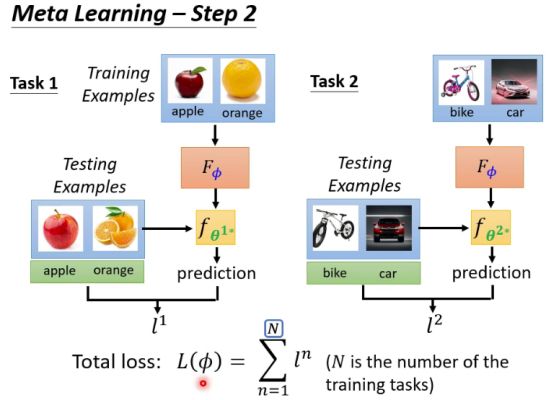
通常的机器学习是针对一个特定的任务找到一个能够实现这个任务的function,例如猫和狗的分类任务。而元学习的目标就是要找到一个Function能够让机器自动学习原来人为确定的一些超参(Hyper-parameter),如初始化参数 θ 0 \theta_0 θ0、学习速率 η \eta η、网络架构等,元学习的分类就是看学习的是什么超参。这个Function用 F ϕ F_{\phi} Fϕ表示, F ϕ F_{\phi} Fϕ不是针对某一个特定任务的,而是针对一群类似的任务,例如这些任务可能包括猫和狗的分类、橘子和苹果的分类、自行车和摩托车的分类等等。这个 F ϕ F_{\phi} Fϕ是要帮这一群类似任务找到一个好的超参,在下次再遇到相似任务的时候,初始化参数可以直接用上,用不着我们再调参了。

元学习是跨任务学习(multi-task learning),因此它需要收集多个类似任务的数据集。比如针对图片二分类任务,我们需要收集橙子和苹果训练数据和测试数据、自行车和汽车的训练数据和测试数据等等许多二分类任务的数据集。元学习的目标是:利用 F ϕ F_{\phi} Fϕ找到最优的超参 ϕ \phi ϕ,使各任务在超参 ϕ \phi ϕ的基础上训练出最优参数后测试得到的损失值 l n l^n ln的和最小。这句话讲起来比较难以理解,举个例子比较好明白:对于苹果和橙子的分类任务,在超参 ϕ \phi ϕ的基础上利用训练数据集进行训练,得到最优参数 θ 1 ∗ \theta^{1*} θ1∗,然后再利用测试数据集对训练后的模型进行测试,测试得到的损失值使 l 1 l^1 l1;同理,可以得到自行车和汽车分类任务的测试损失值 l 2 l^2 l2,以及其他二分类任务的测试损失值 l n l^n ln;元学习的目标就是要找到最优超参 ϕ \phi ϕ,使所有任务的测试损失值之和最小。所以元学习的损失函数定义为, L ( ϕ ) = ∑ n = 1 N l n L(\phi)=\sum_{n=1}^N{l^n} L(ϕ)=n=1∑Nln这里每一个用于训练超参 ϕ \phi ϕ的任务都称为训练任务,上面的N指所有训练任务的总数。如果在拿一个新的任务(该任务未在训练任务中出现过)来测试通过训练找到的超参 ϕ \phi ϕ的效果,那么这个任务就称为测试任务。
我们可以看到在每一个训练任务中包含了训练数据和测试数据,当然在测试任务中也包含了训练数据和测试数据,这和普通机器学习是大不同的。这样听起来很容易让人迷糊,所以有的文献不叫训练数据和测试数据,而是把训练数据叫支持集(support set),把测试数据叫查询集(query set)。
元学习的目标是要找到超参 ϕ \phi ϕ最小化损失函数 L ( ϕ ) L(\phi) L(ϕ)如果能够计算梯度,那么用梯度下降法求解即可。但是有很多情况使无法求梯度的,例如对网络架构的优化,此时有些文献会采用强化学习或进化算法等方法进行求解。

11.2 MAML
11.2.1 MAML概述
在普通机器学习中,初始化参数往往是随机生成的,MAML聚焦于学习一个最好的初始化参数 ϕ \phi ϕ。初始参数 ϕ \phi ϕ不同,对于同一个任务 n n n训练得到的最优参数 θ ^ n \hat{\theta}^n θ^n不同,在任务 n n n的测试数据集上损失值 l n ( θ ^ n ) l^n(\hat{\theta}^n) ln(θ^n)不同。MAML的目标是找到最优的初始参数 ϕ \phi ϕ,是所有任务的测试损失值最小,在遇到新任务时,只需基于少量标签对初始化参数 ϕ \phi ϕ进行微调就可以获得很好的效果。这和前面提到的预训练有些相似,但也有些不同。

11.2.2 MAML的训练
MAML的训练使用梯度下降法: ϕ ← ϕ − η ∇ ϕ L ( ϕ ) \phi \leftarrow \phi-\eta \nabla_{\phi} L(\phi) ϕ←ϕ−η∇ϕL(ϕ)具体的数学推导不管它了,我们直接看上面的梯度下降是如何实施的(这里假设batch size是1):
- ①假设刚开始的初始化参数的初始化参数是 ϕ 0 \phi_0 ϕ0
- ②随机采样一个训练任务 m m m
- ③通过训练任务 m m m的支持集(训练数据)求loss,然后更新一次参数得到任务 m m m的最优参数 θ ^ m \hat{\theta}^m θ^m,注意此时并没有更新 ϕ \phi ϕ。
- ④通过训练任务 m m m的查询集(测试数据)再求一次loss,计算梯度,然后用此梯度的方向更新 ϕ \phi ϕ
- ⑤回到②,重复②③④
上述过程有一个很值得关注的地方是,对于任务 m m m,更新一次参数就认为参数最优了,李宏毅认为作者之所以这么设置是因为MAML主要用于小样本学习,更新一次是怕发生过拟合的问题。
之前说MAML和与训练模型很像,但是也有所不同。不同点是与训练模型用任务的训练数据求loss就直接更新 ϕ \phi ϕ了,而不是在测试数据上二次求loss后才更新的。
结合上面的讲解,来看一看MAML原文的算法,如下图所示。首先随机在这个算法里采样一个batch的训练任务,注意这里的batch是任务而不是数据。对于这一个batch的所有任务:第5行对每一个训练任务 T i T_i Ti,通过支持集求loss,计算梯度;第6行根据第5行算出来的梯度更新一次参数得到 θ i ′ \theta'_i θi′,并且保存起来。假设一个batch有10个任务,那么这里就保存了10个模型参数 θ i ′ \theta'_i θi′。完成了一个batch所有任务的参数更新后,进行第8行:基于更新后的参数和所有任务的查询集计算出各自的loss,将这些loss求和,计算出梯度,利用该梯度更新初始参数。假设一个batch有10个任务,基于更新后的参数和这10个batch任务的查询集计算出10个loss,将这10个loss进行求和,并基于求和结果计算梯度,利用该梯度更新初始参数。

我截了一部分MAML的代码,通过分析代码就可以更好理解上述参数的更新过程了。以下是第一次更新参数的代码
for k in range(1, self.update_step):
# 1.在支持集上计算loss
logits = self.net(x_spt[i], fast_weights, bn_training=True)
loss = F.cross_entropy(logits, y_spt[i])
# 2. 利用上面的loss,计算梯度
grad = torch.autograd.grad(loss, fast_weights)
# 3. 更新参数:theta_pi = theta_pi – train_lr * grad
fast_weights = list(map(lambda p: p[1] – self.update_lr * p[0], zip(grad, fast_weights)))
# 4.基于更新后的参数,在查询集上计算loss
logits_q = self.net(x_qry[i], fast_weights, bn_training=True)
loss_q = F.cross_entropy(logits_q, y_qry[i])
# 5把所有loss加起来,并保存.
losses_q[k + 1] += loss_q
以下是第二次更新参数的代码
# 将所有任务的查询集上的loss的和除以任务数目,求了个平均值
loss_q = losses_q[-1] / task_num
# 利用上面的loss算梯度,并更新初始化参数
self.meta_optim.zero_grad()
loss_q.backward()
self.meta_optim.step()
11.3 元学习在N-ways K-shot上的应用
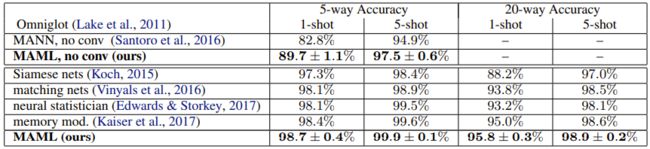
N-way K-shot是典型的小样本学习问题。所谓N-way K-shot是指在每一个任务里面,有N个类别,每个类别有K个样本。Omniglot是一个典型例子它包含1632个不同的字符,每个字符只有20个样本。从上面1632字符中可以构建N-way K-shot任务。例如通过下面的方式构建一个小样本分类任务:抽出20个字符出来,里面每个字符只有1个样本,我们把这个数据集作为训练集(支持集),那就是20-ways 1-shot的问题。然后再在这20个字符中取1个样本出来,作为测试集(查询集),利用训练出来的模型来判断这个样本属于哪个字符。通过这种方式,可以构建出许多任务来,如果是20 ways的就可以构建出81个任务。这些任务又可以分为训练任务和测试任务,例如将81个任务中的60个任务作为训练任务,21个任务作为测试任务。

拥有了这些数据集后,就可以来测试MAML了。以下是MAML原文的测试结果。从测试结果来看,MAML处理N-way K-shot任务是非常棒的。