卡尔曼滤波详解
1.背景介绍.
卡尔曼滤波无论是在工程控制、目标跟踪、SLAM等,对于数据的处理滤波非常重要。本文就撸一撸,谈一谈卡尔曼滤波。
2. 相互独立条件与高斯分布融合
A,B为相互独立的条件:即事件A(或B)是否发生对事件B(A)发生的概率没有影响。那么,AB 同时发生P(AB)=P(A)P(B)。
假如A,B都服从高斯分布: N ( x , u , σ ) = 1 σ ∗ 2 π e − ( x − u ) 2 2 σ 2 \mathcal{N}(x,u,\sigma)=\frac{1}{\sigma*\sqrt{2\pi}}e^{-\frac{(x-u)^2}{2\sigma^2}} N(x,u,σ)=σ∗2π1e−2σ2(x−u)2
有高斯分布1: N 1 ( x , u 1 , σ 1 ) \mathcal{N1}(x,u1,\sigma1) N1(x,u1,σ1)
有高斯分布2: N 2 ( x , u 2 , σ 2 ) \mathcal{N2}(x,u2,\sigma2) N2(x,u2,σ2)
对分布进行融合:
N 1 ( x , u 1 , σ 1 ) ∗ N 2 ( x , u 2 , σ 2 ) = 1 σ 1 σ 2 ∗ 2 π e ( − ( x − u 1 ) 2 2 σ 1 2 − ( x − u 2 ) 2 2 σ 2 2 ) \mathcal{N1}(x,u1,\sigma1)*\mathcal{N2}(x,u2,\sigma2)=\frac{1}{\sigma1\sigma2*2\pi}e^{(-\frac{(x-u1)^2}{2\sigma1^2}-\frac{(x-u2)^2}{2\sigma2^2})} N1(x,u1,σ1)∗N2(x,u2,σ2)=σ1σ2∗2π1e(−2σ12(x−u1)2−2σ22(x−u2)2)
对于上式,可以转化成如下格式(初中知识,自行变换):
N 1 ( x , u 1 , σ 1 ) ∗ N 2 ( x , u 2 , σ 2 ) = S ∗ 1 σ ′ ∗ 2 π e − ( x − u ′ ) 2 2 σ ′ 2 − − − − − − 新高斯分布 N ( x , u ′ , σ ′ ) \mathcal{N1}(x,u1,\sigma1)*\mathcal{N2}(x,u2,\sigma2)=S*\frac{1}{\sigma'*\sqrt{2\pi}}e^{-\frac{(x-u')^2}{2\sigma'^2}} ------新高斯分布\mathcal{N} (x,u',\sigma') N1(x,u1,σ1)∗N2(x,u2,σ2)=S∗σ′∗2π1e−2σ′2(x−u′)2−−−−−−新高斯分布N(x,u′,σ′)
其中:
S = 1 2 π ( σ 1 2 + σ 2 2 ) e − ( u 1 − u 2 ) 2 2 ( σ 1 2 + σ 2 2 ) S=\frac{1}{\sqrt{2\pi(\sigma1^2+\sigma2^2)}}e^{-\frac{(u1-u2)^2}{2(\sigma1^2+\sigma2^2)}} S=2π(σ12+σ22)1e−2(σ12+σ22)(u1−u2)2
u ′ = σ 1 2 u 1 + σ 2 2 u 2 σ 1 2 + σ 2 2 u'=\frac{\sigma1^2u1+\sigma2^2u2}{\sigma1^2+\sigma2^2} u′=σ12+σ22σ12u1+σ22u2
σ ′ = σ 1 2 σ 2 2 σ 1 2 + σ 2 2 \sigma'=\sqrt{\frac{\sigma1^2\sigma2^2}{\sigma1^2+\sigma2^2}} σ′=σ12+σ22σ12σ22
因此,两个高斯分布相乘依旧是高斯分布(需要归一化,u’,a’不变,进行拉伸),图解如下:
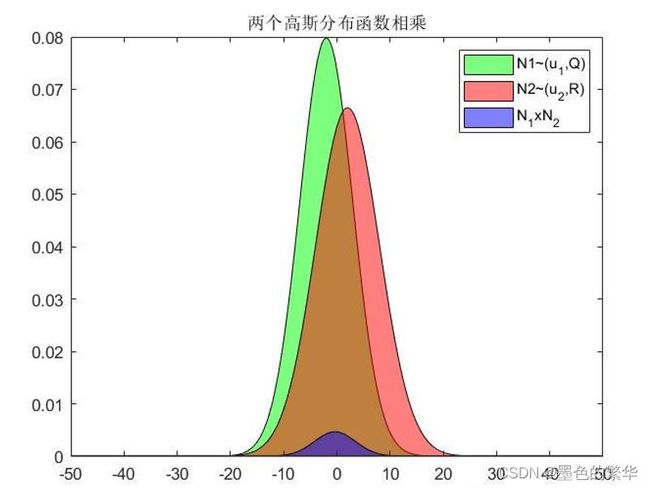
结论:对于两个相关独立的高斯分布条件,其联合分布依旧是高斯分布。
3. 卡尔曼滤波过程
一个过程分为0,1…,k-1,k .时刻。由k-1时刻到k时刻,系统状态预测方程:
X k = A X k − 1 + B u k + w k X_k=AX_{k-1}+Bu_k+w_k Xk=AXk−1+Buk+wk
系统状态观测方程:
Z k = H X k + V k Z_k=HX_k+V_k Zk=HXk+Vk
变量说明
X k X_k\quad Xk:为k时系统状态预测值,包含了噪声。即:k时,状态真值。
X k X_k\quad Xk:为k-1时系统状态预测值,包含了噪声。
A \quad :状态转移矩阵。
如: 物体状态是 X k = ∣ p k v k ∣ X_k=\begin{vmatrix}p_k \\ v_k\end{vmatrix} Xk=∣ ∣pkvk∣ ∣。p:位置;v:速度,假设为直线运动,加速度为 a a a。在d t事件内:
p k = 1 ∗ p k − 1 + d t ∗ v k − 1 + 1 2 d t 2 ∗ a p_k=1*p_{k-1}+dt*v_{k-1}+\frac{1}{2}dt^2*a pk=1∗pk−1+dt∗vk−1+21dt2∗a
v k = 0 ∗ p k − 1 + 1 ∗ v k − 1 + d t ∗ a v_k=0*p_{k-1}+1*v_{k-1}+dt*a vk=0∗pk−1+1∗vk−1+dt∗a
则: ∣ p k v k ∣ = ∣ 1 d t 0 1 ∣ ∣ p k − 1 v k − 1 ∣ + ∣ 1 2 d t 2 d t ∣ a \begin{vmatrix}p_k \\ v_k\end{vmatrix}=\begin{vmatrix}1&dt \\ 0&1\end{vmatrix}\begin{vmatrix}p_{k-1} \\ v_{k-1}\end{vmatrix}+\begin{vmatrix}\frac{1}{2}dt^2 \\dt\end{vmatrix}a ∣ ∣pkvk∣ ∣=∣ ∣10dt1∣ ∣∣ ∣pk−1vk−1∣ ∣+∣ ∣21dt2dt∣ ∣a
其中: ∣ 1 d t 0 1 ∣ \begin{vmatrix}1&dt \\ 0&1\end{vmatrix} ∣ ∣10dt1∣ ∣ 为状态转移矩阵, ∣ 1 2 d t 2 d t ∣ \begin{vmatrix}\frac{1}{2}dt^2 \\dt\end{vmatrix} ∣ ∣21dt2dt∣ ∣为输入增益矩阵
B \qquad :输入增益矩阵,上述示例中的 ∣ 1 2 d t 2 d t ∣ \begin{vmatrix}\frac{1}{2}dt^2 \\dt\end{vmatrix} ∣ ∣21dt2dt∣ ∣
u k u_k\quad uk:系统输入向量,上述示例中的 a a a.
w k w_k\quad wk:过程噪声,均值为0,协方差矩阵为Q,且服从正态分布。
Z k Z_k\quad Zk: 测量数据
v k v_k\quad vk:测量噪声,均值为0,协方差矩阵为R,且服从正态分布。
定义上述方程后,进行迭代。
迭代过程中变量说明
x k x_k xk:真实值
x ^ k \hat{x}_k x^k:卡尔曼估计值
P k P_k Pk:卡尔曼估计误差协方差矩阵
x k ^ ′ {\hat{x_k}}' xk^′:预测值
P k ′ {P_k}' Pk′:预测误差协方差矩阵
K k K_k Kk:卡尔曼增益
z ^ k \hat{z}_k z^k:测量余量
- 预测:
x ^ k ′ = A x ^ k − 1 + B u k \hat{x}'_k=A\hat{x}_{k-1}+Bu_{k} x^k′=Ax^k−1+Buk
P k ′ = A P k − 1 A T + Q {P}'_k=AP_{k-1}A^T+Q Pk′=APk−1AT+Q - 校正:
z ^ k = z k − H x ^ k ′ \hat{z}_k=z_k-H\hat{x}'_k z^k=zk−Hx^k′
K k = P k ′ H T ( H P k ′ H T + R ) − 1 K_k={P}'_kH^T(H{P}'_kH^T+R)^{-1} Kk=Pk′HT(HPk′HT+R)−1
x ^ k = x ^ k ′ + K k z ^ k \hat{x}_k=\hat{x}'_k+K_k\hat{z}_k x^k=x^k′+Kkz^k
更新协方差估计:
P k = ( I − K k H ) P k ′ P_k=(I-K_kH){P}'_k Pk=(I−KkH)Pk′
循环迭代
4. 卡尔曼滤波算法详细推导
1、协方差矩阵
P = E [ ( X − E [ X ] ) ( X − E [ X ] ) T P=E[(X-E[X])(X-E[X])^\mathsf{T} P=E[(X−E[X])(X−E[X])T
= ( c i j ) n × n =(c_{ij})_{n\times_n} =(cij)n×n
= [ c 11 c 12 . . . c 1 n c 21 c 22 . . . c 2 n . . . . . . c n 1 c n 2 . . . c n n ] =\begin{bmatrix} c_{11}&c_{12}&...&c_{1n} \\ c_{21}&c_{22}&...&c_{2n} \\ .&.&...&. \\ c_{n1}&c_{n2}&...&c_{nn}\end{bmatrix} =⎣ ⎡c11c21.cn1c12c22.cn2............c1nc2n.cnn⎦ ⎤
其中:
c ( i j ) = C o v ( x i , x j ) , i , j = 1 , 2 , 3 , . . . , n c_(ij)=Cov(x_i,x_j) , \quad i,j=1,2,3,...,n c(ij)=Cov(xi,xj),i,j=1,2,3,...,n
= E [ ( x i − E ( x i ) ) ( x j − E ( x j ) ) ] \qquad=E[(x_i-E(x_i))(x_j-E(x_j))] =E[(xi−E(xi))(xj−E(xj))]
n:为系统状态的参数的维度
2、协方差矩阵
i 矩阵的微分:
y为标量,X为矩阵
d(y)/d(X) 是一个矩阵的微分,其中的元素 (i,j) 为 d(y)/d(Xi,j)
ii 矩阵的迹:
方阵 A n × n A_{n\times n} An×n的迹定义为对角线元素的和:
t r ( A ) = ∑ a i i = a 11 + a 22 + . . . + a n n tr(A)=\sum a_{ii}=a_{11}+a_{22}+...+a_{nn} tr(A)=∑aii=a11+a22+...+ann
iii 两个矩阵微分公式:
公式一:
∂ t r ( A B ) ∂ A = B T \frac{\partial tr(AB)}{\partial A}=B^T ∂A∂tr(AB)=BT
公式二:
∂ t r ( A B A T ) ∂ A = 2 A B \frac{\partial tr(ABA^T)}{\partial A}=2AB ∂A∂tr(ABAT)=2AB
iv 开始推导:
真实值: x k x_k xk
预测值: x k ^ ′ {\hat{x_k}}' xk^′
估计值: x k ^ {\hat{x_k}} xk^
真实值与预测值之间的误差为: e k ′ = x k − x k ^ e_k'=x_k-{\hat{x_k}} ek′=xk−xk^
预测误差协方差矩阵: P k ′ = E [ e k ′ e k ′ T ] = E [ ( x k − x k ^ ) ( x k − x k ^ ) T ] P_k'=E[e_k' e_k'^T]=E[(x_k-{\hat{x_k}})(x_k-{\hat{x_k}})^T] Pk′=E[ek′ek′T]=E[(xk−xk^)(xk−xk^)T]
= E [ ( A x k − 1 + B u k + w k − A x ^ k − 1 − B u k ) ( A x k − 1 + B u k + w k − A x ^ k − 1 − B u k ) T ] \qquad\qquad\qquad=E[ (A{x}_{k-1}+Bu_{k}+w_k-A\hat x_{k-1}-Bu_k) (A{x}_{k-1}+Bu_{k}+w_k-A\hat x_{k-1}-Bu_k)^T] =E[(Axk−1+Buk+wk−Ax^k−1−Buk)(Axk−1+Buk+wk−Ax^k−1−Buk)T]
= E [ ( A x k − 1 + w k − A x ^ k − 1 ) ( A x k − 1 + w k − A x ^ k − 1 ) T ] \qquad\qquad\qquad=E[ (A{x}_{k-1}+w_k-A\hat x_{k-1})(A{x}_{k-1}+w_k-A\hat x_{k-1})^T] =E[(Axk−1+wk−Ax^k−1)(Axk−1+wk−Ax^k−1)T]
= E [ ( A ( x k − 1 − x ^ k − 1 ) + w k ) ( A ( x k − 1 − x ^ k − 1 ) + w k ) T ] \qquad\qquad\qquad=E[(A(x_{k-1}-\hat x_{k-1})+w_k)(A(x_{k-1}-\hat x_{k-1})+w_k)^T] =E[(A(xk−1−x^k−1)+wk)(A(xk−1−x^k−1)+wk)T]
= E [ ( A e k − 1 + w k ) ( e k − 1 T A T + w k T ) ] \qquad\qquad\qquad =E[(Ae_{k-1}+w_k)(e_{k-1}^TA^T+w_k^T)] =E[(Aek−1+wk)(ek−1TAT+wkT)]
= E [ ( A e k − 1 ) ( A e k − 1 ) T ] + E [ w k w k T ] + 0 + 0 − − − − − − − − 注: E [ w k ] = 0 E [ w k T ] = 0 \qquad\qquad\qquad =E[(Ae_{k-1})(Ae_{k-1})^T]+E[w_kw_k^T]+0+0\quad --------注:E[w_k]=0\quad E[w_k^T]=0 =E[(Aek−1)(Aek−1)T]+E[wkwkT]+0+0−−−−−−−−注:E[wk]=0E[wkT]=0
= A P k − 1 A T + Q \qquad\qquad\qquad =AP_{k-1}A^T+Q =APk−1AT+Q
真实值与估计值之间的误差: e k = x k − x ^ k e_k=x_k-\hat x_k ek=xk−x^k
= x k − ( x ^ k ′ + K k ( z k − H x ^ k ) ) \qquad\qquad\qquad \qquad \qquad =x_k-(\hat x_k'+K_k(z_k-H\hat x_k)) =xk−(x^k′+Kk(zk−Hx^k))
= x k − ( x ^ k ′ + K k ( H x k + v k − H x ^ k ′ ) ) \qquad\qquad\qquad \qquad \qquad =x_k-(\hat x_k'+K_k(Hx_k+v_k-H\hat x_k')) =xk−(x^k′+Kk(Hxk+vk−Hx^k′))
= x k − ( x ^ k ′ + K k ( H x k + v k − H x ^ k ′ ) ) \qquad\qquad\qquad \qquad \qquad =x_k-(\hat x_k'+K_k(Hx_k+v_k-H\hat x_k')) =xk−(x^k′+Kk(Hxk+vk−Hx^k′))
= ( x k − x ^ k ′ ) − K k H ( x k − x ^ k ′ ) − K k v k \qquad\qquad\qquad \qquad \qquad =(x_k-\hat x_k')-K_kH(x_k-\hat x_k')-K_k v_k =(xk−x^k′)−KkH(xk−x^k′)−Kkvk
= ( I − K k H ) ( x k − x ^ k ′ ) − K k v k \qquad\qquad\qquad \qquad \qquad =(I-K_kH)(x_k-\hat x_k')-K_k v_k =(I−KkH)(xk−x^k′)−Kkvk
卡尔曼估计误差协方差矩阵: P k = E [ e k e k T ] \quad P_k=E[e_ke_k^T] Pk=E[ekekT]
因此: P k = E [ ( ( I − K k H ) ( x k − x ^ k ′ ) − K k v k ) ( ( I − K k H ) ( x k − x ^ k ′ ) − K k v k ) T ] \qquad P_k=E[((I-K_kH)(x_k-\hat x_k')-K_k v_k)((I-K_kH)(x_k-\hat x_k')-K_k v_k)^T] Pk=E[((I−KkH)(xk−x^k′)−Kkvk)((I−KkH)(xk−x^k′)−Kkvk)T]
由于$E[v_k]=0 化简上式:
P k = ( I − K k H ) E [ ( x k − x ^ k ′ ) ( x k − x ^ k ′ ) T ] ( I − K k H ) T + K k E [ v k v k T ] K k T P_k=(I-K_kH)E[(x_k-\hat x_k')(x_k-\hat x_k')^T](I-K_kH)^T+K_kE[v_kv_k^T]K_k^T Pk=(I−KkH)E[(xk−x^k′)(xk−x^k′)T](I−KkH)T+KkE[vkvkT]KkT
= ( I − K k H ) E [ ( x k − x ^ k ′ ) ( x k − x ^ k ′ ) T ] ( I − K k H ) T + K k R K k T \qquad =(I-K_kH)E[(x_k-\hat x_k')(x_k-\hat x_k')^T](I-K_kH)^T+K_kRK_k^T =(I−KkH)E[(xk−x^k′)(xk−x^k′)T](I−KkH)T+KkRKkT
= ( I − K k H ) P k ′ ( I − K k H ) T + K k R K k T \qquad =(I-K_kH)P_{k}'(I-K_kH)^T+K_kRK_k^T =(I−KkH)Pk′(I−KkH)T+KkRKkT
卡尔曼滤波本质是最小均方差估计,而均方差是协方差P_k的迹,将上式展开并求迹:
(注意使用迹的公式: t r ( A ) = t r ( A T ) t r ( A B C ) = t r ( C A B ) t r ( A B ) = t r ( A T B ) tr(A)=tr(A^T)\qquad tr(ABC)=tr(CAB)\qquad tr(AB)=tr(A^TB) tr(A)=tr(AT)tr(ABC)=tr(CAB)tr(AB)=tr(ATB)
t r ( P k ) = t r ( ( I − K k H ) P k ′ ( I − K k H ) T + K k R K k T ) tr(P_k)=tr((I-K_kH)P_{k}'(I-K_kH)^T+K_kRK_k^T) tr(Pk)=tr((I−KkH)Pk′(I−KkH)T+KkRKkT)
= t r ( ( I − K k H ) ( I − K k H ) T P k ′ + K k R K k T ) \qquad \quad=tr((I-K_kH)(I-K_kH)^TP_{k}'+K_kRK_k^T) =tr((I−KkH)(I−KkH)TPk′+KkRKkT)
= t r ( ( I − K k H ) ( I − H T K k T ) P k ′ + K k R K k T ) \qquad \quad=tr((I-K_kH)(I-H^TK_k^T)P_{k}'+K_kRK_k^T) =tr((I−KkH)(I−HTKkT)Pk′+KkRKkT)
= t r ( ( I − K k H ) ( I − H T K k T ) P k ′ + K k R K k T ) \qquad \quad=tr((I-K_kH)(I-H^TK_k^T)P_{k}'+K_kRK_k^T) =tr((I−KkH)(I−HTKkT)Pk′+KkRKkT)
= t r ( P k ′ ) − 2 t r ( K k H P k ′ ) + t r ( K k H H T K k T P k ′ ) + t r ( K k R K k T ) \qquad\quad=tr(P_{k}')-2tr(K_kHP_k')+tr(K_kHH^TK_k^TP_k')+tr(K_kRK_k^T) =tr(Pk′)−2tr(KkHPk′)+tr(KkHHTKkTPk′)+tr(KkRKkT)
= t r ( P k ′ ) − 2 t r ( K k H P k ′ ) + t r ( K k H P k ′ H T K k T ) + t r ( K k R K k T ) \qquad\quad=tr(P_{k}')-2tr(K_kHP_k')+tr(K_kHP_k'H^TK_k^T)+tr(K_kRK_k^T) =tr(Pk′)−2tr(KkHPk′)+tr(KkHPk′HTKkT)+tr(KkRKkT)
= t r ( P k ′ ) − 2 t r ( K k H P k ′ ) + t r ( K k ( H P k ′ H T + R ) K k T ) \qquad\quad=tr(P_{k}')-2tr(K_kHP_k')+tr(K_k(HP_k'H^T+R)K_k^T) =tr(Pk′)−2tr(KkHPk′)+tr(Kk(HPk′HT+R)KkT)
∂ t r ( P k ) ∂ K k = ∂ t r ( P k ′ ) − 2 t r ( K k H P k ′ ) + t r ( K k ( H P k ′ H T + R ) K k T ) ∂ K k \frac{\partial tr(P_k)}{\partial K_k}=\frac{\partial tr(P_{k}')-2tr(K_kHP_k')+tr(K_k(HP_k'H^T+R)K_k^T)}{\partial K_k} ∂Kk∂tr(Pk)=∂Kk∂tr(Pk′)−2tr(KkHPk′)+tr(Kk(HPk′HT+R)KkT)
使用两个矩阵微分公式:有
∂ t r ( P k ) ∂ K k = 0 − 2 ( H P k ′ ) T + 2 K r ( H P k ′ H T + R ) \frac{\partial tr(P_k)}{\partial K_k}=0-2(HP_k')^T+2K_r(HP_k'H^T+R) ∂Kk∂tr(Pk)=0−2(HPk′)T+2Kr(HPk′HT+R)
令 ∂ t r ( P k ) ∂ K k = 0 \frac{\partial tr(P_k)}{\partial K_k}=0 ∂Kk∂tr(Pk)=0
K k ( H P k ′ H T + R ) = P k ′ H T K_k(HP_k'H^T+R)=P_k'H^T Kk(HPk′HT+R)=Pk′HT
K k = P k ′ H T ( H P k ′ H T + R ) K_k=\frac{P_k'H^T}{(HP_k'H^T+R)} Kk=(HPk′HT+R)Pk′HT
因此:有上一次的后验协方差 P k − 1 P_{k-1}\qquad Pk−1—> 本次的先验协方差: P k ′ = A P k − 1 A T + Q P_k'=AP_{k-1}A^T+Q\qquad Pk′=APk−1AT+Q —>本次的卡尔曼增益: K k = P k ′ H T ( H P k ′ H T + R ) K_k=\frac{P_k'H^T}{(HP_k'H^T+R)}\qquad Kk=(HPk′HT+R)Pk′HT —>本次的最优状态:卡尔曼估计值 \qquad —> 本次的后验协方差 P k = ( I − K k H ) P k ′ P_k=(I-K_kH){P}'_k Pk=(I−KkH)Pk′,为下一次准备。
5. Python卡尔曼滤波
```python
import numpy as np
import matplotlib.pyplot as plt
##下面是通过高斯正态分布产生误差
def gaussian_distribution_generator(var):
return np.random.normal(loc=0.0, scale=var, size=None) ##np.random.normal是正态分布
# 参数loc(float):正态分布的均值,对应着这个分布的中心。loc=0说明这一个以Y轴为对称轴的正态分布,
# 参数scale(float):正态分布的标准差,对应分布的宽度,scale越大,正态分布的曲线越矮胖,scale越小,曲线越高瘦。
# 参数size(int 或者整数元组):输出的值赋在shape里,默认为None。
# 状态转移矩阵,上一时刻的状态转移到当前时刻
A = np.array([[1, 1],
[0, 1]])
# 过程噪声协方差矩阵Q,p(w)~N(0,Q),噪声来自真实世界中的不确定性 N(0,Q) 表示期望是0,协方差矩阵是Q
Q = np.array([[0.1, 0], # Q其实就是过程的协方差
[0, 0.1]]) # 过程的协方差越小,说明预估的越准确
# 观测噪声协方差矩阵R,p(v)~N(0,R) 也是测量的协方差矩阵
R = np.array([[1, 0], # R其实就是测量的协方差矩阵
[0, 1]]) #测量的协方差越小,说明测量的结果更准确
# 状态观测矩阵
H = np.array([[1, 0],
[0, 1]])
# 控制输入矩阵B
B = None
# 初始位置与速度
X0 = np.array([[0], # 二维的,定义初始的位置和速度,初始的位置为0 ,速度为1
[1]])
# 状态估计协方差矩阵P初始化(其实就是初始化最优解的协方差矩阵)
P = np.array([[1, 0],
[0, 1]])
if __name__ == "__main__":
# ---------------------------初始化-------------------------
X_true = np.array(X0) # 真实状态初始化
X_posterior = np.array(X0) # X_posterior表示上一时刻的最优估计值
P_posterior = np.array(P) # P_posterior是继续更新最优解的协方差矩阵
speed_true = [] # 实际的速度值
position_true = [] # 实际的位置值
speed_measure = [] # 测量到的速度值
position_measure = [] # 测量到的位置值
speed_prior_est = [] # 速度的先验误差 估计值
position_prior_est = [] # 位置的先验误差 估计值
speed_posterior_est = [] # 根据估计值及当前时刻的观测值融合到一体得到的最优估计速度值存入到列表中
position_posterior_est = [] # 根据估计值及当前时刻的观测值融合到一体得到的最优估计值位置值存入到列表中
for i in range(30):
# -----------------------生成真实值----------------------
# 生成过程噪声
# 通过Q矩阵产生误差
w = np.array(
[[gaussian_distribution_generator(Q[0, 0])], # gaussian_distribution_generator(Q[0, 0])的值为0.01103097596,(这值是随机的,每次运行都不一样)
[gaussian_distribution_generator(Q[1, 1])]]) # gaussian_distribution_generator(Q[1, 1])的值为-0.1242726240,(这值是随机的,每次运行都不一样)
X_true = np.dot(A, X_true) + w # 得到当前时刻实际的速度值和位置值,其中A是状态转移矩阵上一时刻的状态转移到当前时刻
speed_true.append(X_true[1, 0]) # 将第二行第一列位置的数值,1.01103098添加到列表speed_true里面
position_true.append(X_true[0, 0]) # 将第一行第一列位置的数值,1.01103098添加到列表position_true里面
# -----------------------生成观测值----------------------
# 生成观测噪声
##通过R矩阵产生误差
v = np.array(
[[gaussian_distribution_generator(R[0, 0])], # gaussian_distribution_generator(R[0, 0])的值为-0.62251186549,(这值是随机的,每次运行都不一样)
[gaussian_distribution_generator(R[1, 1])]]) # gaussian_distribution_generator(R[1, 1])的值为2.52779100481,(这值是随机的,每次运行都不一样)
Z_measure = np.dot(H, X_true) + v # 生成观测值,H为单位阵E # A是状态观测矩阵 # Z_measure表示测量得到的值
position_measure.append(Z_measure[0, 0])
speed_measure.append(Z_measure[1, 0])
################################################################下面开始进行预测和更新,来回不断的迭代#######################################################################
# ----------------------进行先验估计---------------------
X_prior = np.dot(A,X_posterior) # X_prior表示根据上一时刻的最优估计值得到当前的估计值 X_posterior表示上一时刻的最优估计值
position_prior_est.append(X_prior[0, 0]) # 将根据上一时刻计算得到的最优估计位置值添加到列表position_prior_est中
speed_prior_est.append(X_prior[1, 0]) # 将根据上一时刻计算得到的最优估计速度值添加到列表speed_prior_est.append中
# 计算状态估计协方差矩阵P
P_prior_1 = np.dot(A,P_posterior) # P_posterior是上一时刻最优估计的协方差矩阵 # P_prior_1就为公式中的(A.Pk-1)
P_prior = np.dot(P_prior_1, A.T) + Q # P_prior是得出当前的先验估计协方差矩阵 #Q是过程协方差
# ----------------------计算卡尔曼增益,用numpy一步一步计算Prior and posterior
k1 = np.dot(P_prior, H.T) # P_prior是得出当前的先验估计协方差矩阵
k2 = np.dot(np.dot(H, P_prior), H.T) + R # R是测量的协方差矩阵
K = np.dot(k1, np.linalg.inv(k2)) # np.linalg.inv():矩阵求逆 # K就是当前时刻的卡尔曼增益
# ---------------------后验估计------------
X_posterior_1 = Z_measure - np.dot(H, X_prior) # X_prior表示根据上一时刻的最优估计值得到当前的估计值 # Z_measure表示测量得到的值
X_posterior = X_prior + np.dot(K, X_posterior_1) # K就是当前时刻的卡尔曼增益 # X_posterior是根据估计值及当前时刻的观测值融合到一体得到的最优估计值
position_posterior_est.append(X_posterior[0, 0]) # 根据估计值及当前时刻的观测值融合到一体得到的最优估计位置值存入到列表中
speed_posterior_est.append(X_posterior[1, 0]) # 根据估计值及当前时刻的观测值融合到一体得到的最优估计速度值存入到列表中
# 更新状态估计协方差矩阵P (其实就是继续更新最优解的协方差矩阵)
P_posterior_1 = np.eye(2) - np.dot(K, H) # np.eye(2)返回一个二维数组,对角线上为1,其他地方为0
P_posterior = np.dot(P_posterior_1, P_prior) # P_posterior是继续更新最优解的协方差矩阵 ##P_prior是得出当前的先验估计协方差矩阵
# 可视化显示
if True:
plt.rcParams['font.sans-serif'] = ['SimHei'] # 坐标图像中显示中文
plt.rcParams['axes.unicode_minus'] = False
fig, axs = plt.subplots(1, 2)
axs[0].plot(speed_true, "-", label="speed_true(实际值)", linewidth=1) # Plot some data on the axes.
axs[0].plot(speed_measure, "-", label="speed_measure(测量值)", linewidth=1) # Plot some data on the axes.
axs[0].plot(speed_prior_est, "-", label="speed_prior_est(估计值)", linewidth=1) # Plot some data on the axes.
axs[0].plot(speed_posterior_est, "-", label="speed_posterior_est(融合测量值和估计值)",
linewidth=1) # Plot some data on the axes.
axs[0].set_title("speed")
axs[0].set_xlabel('k') # Add an x-label to the axes.
axs[0].legend() # Add a legend.
axs[1].plot(position_true, "-", label="position_true(实际值)", linewidth=1) # Plot some data on the axes.
axs[1].plot(position_measure, "-", label="position_measure(测量值)", linewidth=1) # Plot some data on the axes.
axs[1].plot(position_prior_est, "-", label="position_prior_est(估计值)",
linewidth=1) # Plot some data on the axes.
axs[1].plot(position_posterior_est, "-", label="position_posterior_est(融合测量值和估计值)",
linewidth=1) # Plot some data on the axes.
axs[1].set_title("position")
axs[1].set_xlabel('k') # Add an x-label to the axes.
axs[1].legend() # Add a legend.
plt.show()
import cv2
import numpy as np
def mousemove(event, x, y, s, p):
#
global frame, current_measurement, measurements, last_measurement, current_prediction, last_prediction
#
last_measurement = current_measurement
last_prediction = current_prediction
current_x = np.float32(x)
current_y = np.float32(y)
#
current_measurement = np.array([[current_x], [current_y]])
print("current_measurement", current_measurement)
kalman.correct(current_measurement)
print("new_current_measurement", current_measurement)
#
current_prediction = kalman.predict()
print("current_prediction", current_prediction)
#
lmx, lmy = last_measurement[0], last_measurement[1]
#
cmx, cmy = current_measurement[0], current_measurement[1]
#
lpx, lpy = last_prediction[0], last_prediction[1]
#
cpx, cpy = current_prediction[0], current_prediction[1]
#
cv2.line(frame, (int(lmx), int(lmy)), (int(cmx), int(cmy)), (0, 100, 0))
#
cv2.line(frame, (int(lpx), int(lpy)), (int(cpx), int(cpy)), (0, 0, 200))
if __name__ == '__main__':
frame = np.zeros((800, 800, 3), np.uint8)
last_measurement = current_measurement = np.array((2, 1), np.float32)
last_predicition = current_prediction = np.zeros((2, 1), np.float32)
cv2.namedWindow("kalman_maustracker")
cv2.setMouseCallback("kalman_maustracker", mousemove)
kalman = cv2.KalmanFilter(4, 2)
#
kalman.measurementMatrix = np.array([[1, 0, 0, 0], [0, 1, 0, 0]], np.float32)
#
kalman.transitionMatrix = np.array([[1, 0, 1, 0], [0, 1, 0, 1], [0, 0, 1, 0], [0, 0, 0, 1]], np.float32)
#
kalman.processNoiseCov = np.array([[1, 0, 0, 0], [0, 1, 0, 0], [0, 0, 1, 0], [0, 0, 0, 1]], np.float32) * 0.03
while True:
cv2.imshow("kalman_maustracker", frame)
if (cv2.waitKey(30) & 0xff) == ord('q'): # 按 q 键退出
break
cv2.destroyAllWindows()
cv2.waitKey(1)
