哈工大机器学习复习笔记（四）

本篇文章是在参考西瓜书、PPT课件、网络上相关博客等资料的基础上整理出的机器学习复习笔记，希望能给大家的机器学习复习提供帮助。这篇笔记只是复习的一个参考，大家一定要结合书本、PPT来进行复习，有些公式的推导最好能够自己演算一遍。由于作者水平有限，笔记中难免有些差错，欢迎大家评论留言。
完整版跳转

9. 聚类

9.1 距离

聚类的主要思想是将无标签的数据分为若干个组，其中类内聚集、类间分离。
想要衡量“相似度”，我们需要有对距离的定义。距离必须满足以下条件：

• $D(A,B)=D(B,A)$
• $D(A,A)=0$
• $D(A,B)=0⟺A=B$
• $D(A,B)\le D(A,C)+D(C,B)$
  闵可夫斯基距离定义了一系列距离，$r$阶闵可夫斯基距离是：
  $$d(x,y)=\sqrt[r]{\sum _i|x_i-y_i{|}^r}$$
  显然，$r=1$时为曼哈顿距离，$r=2$时为欧几里得距离（L2范数），$r=+\infty$时是两个向量各个维度之差的绝对值的最大值。
  还有各种其他的距离，例如汉明距离、最小编辑距离等。
  注意：KL距离不满足以上4点。

9.2 K-Means

给定样本集$D$和划分聚类的数量$k$，聚类需要将样本划分为$k$个不相交的簇$C=\{C_1,\dots ,C_k\}$.
算法：

1. 随机初始化$k$个簇中心${\mu }^{(0)}={\mu }_1^{(0)},\dots ,{\mu }_k^{(0)}$
2. 将每个训练样本打上距离其最近的簇中心的标签
   $$C^{(t)}(j)\leftarrow \arg \underset{i}{\min }||{\mu }_i-x_j|{|}^2$$
3. 根据新的$C$重新计算各类的$\mu$，回到第二步继续迭代求解。
   $${\mu }_i^{(t+1)}\leftarrow \arg \underset{\mu }{\min }\sum _{j:C(j)=i}||\mu -x_j|{|}^2$$
   算法迭代终止的条件：当一轮迭代前后每个点所属的类别都不再变化，或者一轮迭代前后，$\mu$的变化很小，小于某个极小值，则停止迭代。
   K-Means算法优化的实际上是样本中所有点到其所属的类别中心的距离之和
   $$F(\mu ,C)=\sum _{j=1}^m||{\mu }_{C(j)}-x_j|{|}^2$$
   优化目标即
   $$\underset{\mu }{\min }\underset{C}{\min }F(\mu ,C)=\underset{\mu }{\min }\underset{C}{\min }\sum _{i=1}^k\sum _{j:C(j)=i}||{\mu }_i-x_j|{|}^2$$

EM算法角度

1. 固定$\mu$，优化$C$（Expectation step）
   $$\underset{C(1),C(2),\dots ,C(m)}{\min }\sum _{j=1}^m||{\mu }_{C(j)}-x_j|{|}^2=\sum _{j=1}^m\underset{C(j)}{\min }||{\mu }_{C(j)}-x_j|{|}^2$$
   即为每个样本分配一个距离最近的簇中心的类标签。
2. 固定$C$，优化$\mu$（Maximization step）
   $$\underset{{\mu }_1.{\mu }_2,\dots ,{\mu }_k}{\min }\sum _{i=1}^k\sum _{j:C(j)=i}||{\mu }_i-x_j|{|}^2=\sum _{i=1}^k\underset{{\mu }_i}{\min }\sum _{j:C(j)=i}||{\mu }_i-x_j|{|}^2$$
   即为每个类重新选取簇中心。

K-Means与EM算法的比较：

• K-means 算法其实是EM算法的一种特殊情况；
• K-Means算法对数据点进行了硬分配，即认为每个数据点只属于唯一的聚类；而EM算法则认为数据点是由多个分布共同生成的。

产生式模型角度

假设数据集来自于$k$个方差相同的高斯分布的混合，不妨设第$i$个分布的均值为${\mu }_i$，且每个分布的协方差阵均为${\sigma }^{2}I$。
每个训练样本产生步骤：

1. 以$P(y=i)$的概率随机选择第$i$个高斯分布
2. 以第$i$个高斯分布产生样本$x\sim N({\mu }_i,{\sigma }^{2}I)$
   即
   $$\begin{gathered} p(x|y=i)\sim N({\mu }_i,{\sigma }^{2}I) \\ p(x)=\sum _{i}p(x|y=i)p(y=i) \end{gathered}$$
   高斯贝叶斯分类器
   $$\begin{array}{rl}\log \frac{P(y=i|x)}{P(y=j|x)}& =\log \frac{P(x|y=i)P(y=i)}{P(x|y=j)P(y=j)}\\ & =\dots \\ & =w^{T}x+b\end{array}$$
   可得这是一个线性决策面（具体推导可参照贝叶斯判别中的决策面推导）。

最大似然（MLE）

由于$y_i$未知（即无法获知$P(x_i,y_i)$），我们选择最大化边缘似然
$$\begin{array}{rl}\arg \max \prod _{j}P(x_j)& =\arg \max \prod _j\sum _{i=1}^{k}P(y_j=i,x_j)\\ & =\arg \max \prod _j\sum _{i=1}^{k}P(y_j=i)P(x_j|y_j=i)\end{array}$$
而每个$x_i$仅可以属于某一个类别（硬指派），即$P(y_j=i)=1\text{ or }0,1\text{ if }i=C(j)$，则$$\begin{array}{rl}\arg \max \log \prod _j\sum _{i=1}^{k}P(y_j=i)P(x_j|y_j=i)& =\arg \max \sum _j\log \sum _{i=1}^{k}P(y_j=i)P(x_j|y_j=i)\\ & \propto \arg \max \sum _j\log (\exp \{-\frac{1}{2}(x_j-{\mu }_{C(j)}{)}^T({\sigma }^{2}I{)}^{-1}(x_j-{\mu }_{C(j)})\})\\ & =\arg \max \sum _j\log (\exp (-\frac{1}{2{\sigma }^2}||x_j-{\mu }_{C(j)}|{|}^2))\\ & =\arg \max \sum _j-\frac{1}{2{\sigma }^2}||x_j-{\mu }_{C(j)}|{|}^2\\ & \propto \arg \max \sum _j-||x_j-{\mu }_{C(j)}|{|}^2\\ & =\arg \min \sum _j||x_j-{\mu }_{C(j)}|{|}^2\end{array}$$
这与K-means的优化目标是相同的。

特点

• K-Means实际上假设数据呈现球形分布，与之相比，GMM假设数据为高斯分布
• K-Means假设各个簇的先验概率相同，但是各个簇的数量可能不均匀
• K-Means的迭代过程实际上等价于EM算法
• 优点：计算复杂度低（$o(N\cdot k\cdot q)$，其中$q$为迭代次数，通常$k$和$q$均小于$N$）；思想简单，容易实现。
• 缺点：需要确定聚类的数量$k$；分类的结果严重依赖于簇中心的初始化；结果不一定是全局最优的，只能保证局部最优；对噪声敏感，无法解决不规则形状的聚类。

9.3 GMM

GMM中假设各类的分布为高斯分布，多元高斯分布生成的$d$维随机变量$x$的密度函数为：
$$p(x|\mu ,\Sigma )=\frac{1}{(2\pi {)}^{\frac{d}{2}}|\Sigma {|}^{\frac{1}{2}}}\exp (-\frac{1}{2}(x-\mu {)}^T{\Sigma }^{-1}(x-\mu ))$$
其中$\mu$为均值向量，$\Sigma$为协方差矩阵。
这里由于各分布的协方差矩阵不一定相同，所以决策面也不一定是线性的。

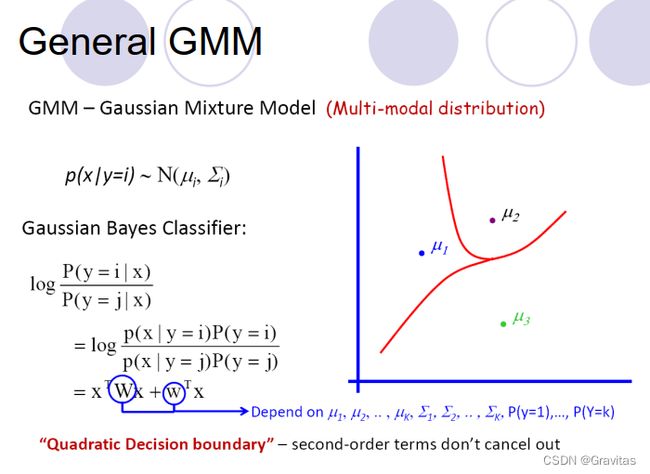
给定训练样本集 $X=\{x_1,x_2,...,x_n\}$，其中$n$为样本数量。对于一个样本$x_i$，我们可以认为它是由多个对应维度的多元高斯分布所生成，可以由⾼斯分布的线性叠加来表征数据，假设数据由$k$个高斯分布混合生成，则
$$p(x_i)=\sum _{j=1}^k{\pi }_{j}p(x_i|u_j,{\Sigma }_j)$$
其中${\mu }_j$和${\Sigma }_j$分别表示第$j$个高斯分布的均值和协方差矩阵，${\pi }_j$为相应的混合系数，满足$\sum _{j=1}^k{\pi }_j=1$。令随机变量$z_j\in \{1,2,...,k\}$表示生成样本$x_j$的高斯混合成分，其取值未知。根据贝叶斯定理，$z_j$的后验分布对应于
$$\gamma (z_j)\equiv p(z_j=i|x_j)=\frac{p(z_j=i)p(x_j|z_j=i)}{p(x_j)}=\frac{{\pi }_{i}p(x_j|{\mu }_i,{\Sigma }_i)}{\sum _{l=1}^k{\pi }_{l}p(x_j|{\mu }_l,{\Sigma }_l)}$$
当后验概率已知时，混合高斯模型将训练样本划分成了$k$个簇$C=C_1,C_2,...,C_k$，对于每一个样本$x_j$，其类别为$i$，满足$i=\arg \underset{i}{\max }\gamma (z_i)$，即选择后验概率最大的类别作为其标签类别。与K-Means类似，由于$y_i$未知（即无法获知$P(x_i,y_i)$），我们选择最大化边缘似然，极大似然函数为
$$LL(D)=\ln p(X|\pi ,\mu ,\Sigma )=\ln \prod _{j=1}^{n}p(x_j)=\sum _{j=1}^n\ln \sum _{i=1}^k{\pi }_{i}p(x_j|{\mu }_i,{\Sigma }_i)$$
使上式最大化，对${\mu }_i$求偏导，并令导数为0，则
$$\frac{\partial \ln p(X|\pi ,\mu ,\Sigma )}{\partial {\mu }_i}=\sum _{j=1}^n\frac{{\pi }_{i}p(x_j|{\mu }_i,{\Sigma }_i)}{\sum _{l=1}^k{\pi }_{l}p(x_j|{\mu }_l,{\Sigma }_l)}{\Sigma }_i^{-1}(x_j-{\mu }_i)=0$$
令
$${\gamma }_{ji}=\frac{p(z_j=i|x_j)}{\sum _{j=1}^{k}p(z_j=i|x_j)}=\frac{{\pi }_{i}p(x_j|{\mu }_i,{\Sigma }_i)}{\sum _{l=1}^k{\pi }_{l}p(x_j|{\mu }_l,{\Sigma }_l)}$$
可解得
$$\begin{array}{rl}{n}_i& =\sum _{j=1}^n{\gamma }_{ji}\\ {\mu }_i& =\frac{1}{n_i}\sum _{j=1}^n{\gamma }_{ji}{x}_j\end{array}$$
同理，对${\Sigma }_i$求导令导数为0：
$$\frac{\partial \ln p(X|\pi ,\mu ,\Sigma )}{\partial {\Sigma }_i}=\sum _{j=1}^n\frac{{\pi }_{i}p(x_j|{\mu }_i,{\Sigma }_i)}{\sum _{l=1}^k{\pi }_{l}p(x_j|{\mu }_l,{\Sigma }_l)}({\Sigma }_i^{-1}-{\Sigma }_i^{-1}(x_j-{\mu }_i)(x_j-{\mu }_i{)}^T{\Sigma }_i^{-1})=0$$
解得
$${\Sigma }_i=\frac{\sum _{j=1}^n{\gamma }_{ji}(x_j-{\mu }_i)(x_j-{\mu }_i{)}^T}{n_i}$$
对于混合系数${\pi }_i$，还需要满足约束条件$\sum _{i=1}^k{\pi }_i=1$。构造拉格朗日多项式：
$$\ln p(X|\pi ,\mu ,\Sigma )+\lambda (\sum _{i=1}^k{\pi }_i-1)$$
对${\pi }_i$求导，令导数为0：
$$\frac{\partial \ln p(X|\pi ,\mu ,\Sigma )+\lambda (\sum _{i=1}^k{\pi }_i-1)}{\partial {\pi }_i}=\sum _{j=1}^n\frac{p(x_j|{\mu }_i,{\Sigma }_i)}{\sum _{l=1}^k{\pi }_{l}p(x_j|{\mu }_l,{\Sigma }_l)}+\lambda =0$$
同乘${\pi }_i$并将$i\in \{1,2,...,k\}$代入相加得：
$$\sum _{i=1}^k{\pi }_i\sum _{j=1}^n\frac{p(x_j|{\mu }_i,{\Sigma }_i)}{\sum _{l=1}^k{\pi }_{l}p(x_{i}j|{\mu }_l,{\Sigma }_l)}+\lambda \sum _{i=1}^k{\pi }_i=0$$
将约束条件代入：
$$\sum _{j=1}^n(\frac{\sum _{i=1}^k{\pi }_{i}p(x_j|{\mu }_i,{\Sigma }_i)}{\sum _{l=1}^k{\pi }_{l}p(x_j|{\mu }_l,{\Sigma }_l)})+\lambda \sum _{i=1}^k{\pi }_i=n+\lambda =0$$
即$$\lambda =-n$$.
又由于
$$\sum _{j=1}^n\frac{p(x_j|{\mu }_i,{\Sigma }_i)}{\sum _{l=1}^k{\pi }_{l}p(x_j|{\mu }_l,{\Sigma }_l)}+\lambda =0$$
且
$${\gamma }_{ji}=\frac{{\pi }_{i}p(x_j|{\mu }_i,{\Sigma }_i)}{\sum _{l=1}^k{\pi }_{l}p(x_j|{\mu }_l,{\Sigma }_l)}$$
故上式可重写为
$$\sum _{j=1}^n\frac{{\gamma }_{ji}}{{\pi }_i}+\lambda =0$$
将$n_i={\sum }_{j=1}^n{\gamma }_{ji}$和$\lambda =-n$代入得
$${\pi }_i=\frac{n_i}{n}$$
GMM算法过程如下：

1. 随机初始化参数${\pi }_i,{\mu }_i,{\Sigma }_i,i\in 1,2,\dots ,k$.
2. E步：根据式${\gamma }_{ji}=\frac{{\pi }_{i}p(x_j|{\mu }_i,{\Sigma }_i)}{\sum _{l=1}^k{\pi }_{l}p(x_j|{\mu }_l,{\Sigma }_l)}$计算每个样本由各个混合高斯成分生成的后验概率.
3. M步：用下面的一系列公式更新参数${\pi }_i,{\mu }_i,{\Sigma }_i,i\in 1,2,\dots ,k$.
   $$\begin{array}{rl}{\mu }_i& =\frac{1}{n_i}\sum _{j=1}^n{\gamma }_{ji}{x}_j\\ {\Sigma }_i& =\frac{\sum _{j=1}^n{\gamma }_{ji}(x_j-{\mu }_i)(x_j-{\mu }_i{)}^T}{n_i}\\ {\pi }_i& =\frac{n_i}{n}\end{array}$$
   其中$n_i={\sum }_{j=1}^n{\gamma }_{ji}$.
4. 重复E步和M步直至收敛.
   算法迭代结束条件：某一次迭代后参数的变化小于一个极小数。

与K-Means算法的对比

• GMM算法收敛前经历了更多次迭代，每次迭代需要更多计算量，通常运行K-Means找到GMM的一个合适的初始化值，接下来使用GMM算法进行微调；
• K-Means算法对数据点进行了硬分配，即每个数据点只属于唯一的聚类；而GMM算法基于后验概率对数据点进行了软分配；
• K-Means算法可以看成GMM算法的特殊形式（没有估计协方差，只估计了聚类的均值）。

10. PCA

10.1 最大方差形式

考虑一个数据集$\{x_1,\dots ,x_N\},x_n\in R^D$，我们的目标是把这些数据投影到一个$M(M<D)$维的空间中。
假设降维至$M$维空间，我们使用$M$个$D$维的单位向量$u_1,u_2,\dots ,u_M$作为这个空间的基向量。由于是单位向量，需满足$u_k^T{u}_k=1,k=1,2,\dots ,M$。
对于数据集中的任意一个样本$x_i$，投影至$u_k$方向后的数据变为$u_k^T{x}_i$，考虑投影后数据的方差（即在$u_k$方向的方差）
$$\frac{1}{N}\sum _{n=1}^N\{u_k^T{x}_n-u_k^T\bar{x}{\}}^2=u_k^{T}S{u}_k$$
其中
$$\begin{array}{rl}\bar{x}& =\frac{1}{N}\sum _{n=1}^N{x}_n\\ S& =\frac{1}{N}\sum _{n=1}^N(x_n-\bar{x})(x_n-\bar{x}{)}^T\end{array}$$
优化函数为
$$\begin{array}{rl}\arg \underset{u_k}{\max }& u_k^{T}S{u}_k\\ s.t.& u_k^T{u}_k=1,k=1,\dots ,M\end{array}$$
对应的拉格朗日函数为
$$L(u_k,{\lambda }_k)=u_k^{T}S{u}_k+{\lambda }_k(1-u_k^T{u}_k)$$
对$u_k$求偏导
$$\frac{\partial L}{\partial u_k}=2S{u}_k-2{\lambda }_k{u}_k=0$$
即
$$S{u}_k={\lambda }_k{u}_k$$
则$u_k$是$S$的特征向量，${\lambda }_k$是对应的特征值。
上式左乘$u_k^T$可以得到
$$u_k^{T}S{u}_k=u_k^T{\lambda }_k{u}_k={\lambda }_k$$
显然，该式对$\forall k=1,2,\dots ,M$均成立。并且由该式可知，最大化方差其实就等价于最大化${\lambda }_k$。因而我们取$S$最大的$M$个特征值对应的特征向量作为基向量。

10.2 最小误差形式

引入$D$维单位正交基集合$\{u_1,\dots ,u_D\}$，且满足
$$u_i^T{u}_j={\delta }_{ij}=\{\begin{array}{ll}1& i=j\\ 0& i\ne j\end{array}$$
这时，每个数据点均可以被精确地表示为基向量的线性组合，即
$$x_n=\sum _{i=1}^D{\alpha }_{ni}{u}_i,{\alpha }_{ni}=x_n^T{u}_i$$
我们的目标时是使用$M(M<D)$维的空间来近似表示原数据点，不失一般性，我们用前$M$个基向量来表示
$${\tilde{x}}_n=\sum _{i=1}^M{z}_{ni}{u}_i+\sum _{i=M+1}^D{b}_i{u}_i$$
其中$z_{ni}$依赖于数据点，$b_i$是常数。
我们的目标是最小化误差
$$J=\frac{1}{N}\sum _{n=1}^N||x_n-{\tilde{x}}_n|{|}^2$$
对上式展开得
$$\begin{array}{rl}J& =\frac{1}{N}\sum _{n=1}^N||x_n-{\tilde{x}}_n|{|}^2\\ & =\frac{1}{N}\sum _{n=1}^N(x_n-{\tilde{x}}_n{)}^T(x_n-{\tilde{x}}_n)\\ & =\frac{1}{N}\sum _{n=1}^N(x_n-\sum _{i=1}^M{z}_{ni}{u}_i-\sum _{i=M+1}^D{b}_i{u}_i{)}^T(x_n-\sum _{i=1}^M{z}_{ni}{u}_i-\sum _{i=M+1}^D{b}_i{u}_i)\\ & =\frac{1}{N}\sum _{n=1}^N(x_n^T-\sum _{i=1}^M{z}_{ni}{u}_i^T-\sum _{i=M+1}^D{b}_i{u}_i^T)(x_n-\sum _{i=1}^M{z}_{ni}{u}_i-\sum _{i=M+1}^D{b}_i{u}_i)\\ & =\frac{1}{N}\sum _{n=1}^N(x_n^T{x}_n-2\sum _{i=1}^M{z}_{ni}{x}_n^T{u}_i-2\sum _{i=M+1}^D{b}_i{x}_n^T{u}_i+\sum _{i=1}^M{z}_{ni}^2+\sum _{i=M+1}^D{b}_i^2)\end{array}$$
$J$对$z_{ni}$和$b_i$分别求偏导得
$$\begin{array}{rl}\frac{\partial J}{\partial z_{ni}}& =\frac{1}{N}(-2x_n^T{u}_i+2z_{ni})=0\\ \frac{\partial J}{\partial b_i}& =\frac{1}{N}\sum _{n=1}^N(-2x_n^T{u}_i+2b_i)=0\end{array}$$
可得
$$\begin{array}{rl}{z}_{ni}& =x_n^T{u}_i\\ b_i& ={\bar{x}}^T{u}_i\end{array}$$
又由于${\alpha }_{ni}=z_{ni},i=1,\dots ,M$，因此
$$\begin{array}{rl}{x}_n-{\tilde{x}}_n& =\sum _{i=1}^D{\alpha }_{ni}{u}_i-(\sum _{i=1}^M{z}_{ni}{u}_i+\sum _{i=M+1}^D{b}_i{u}_i)\\ & =\sum _{i=M+1}^D({\alpha }_{ni}-b_i)u_i\end{array}$$
从而（注意到$u_i^T{u}_j=1⟺i=j$）
$$\begin{array}{rl}||x_n-{\tilde{x}}_n|{|}^2& =(x_n-{\tilde{x}}_n{)}^T(x_n-{\tilde{x}}_n)\\ & =\sum _{i=M+1}^D({\alpha }_{ni}-b_i)u_i^T\cdot \sum _{j=M+1}^D({\alpha }_{nj}-b_j)u_j\\ & =\sum _{i=M+1}^D({\alpha }_{ni}-b_i{)}^2\\ & =\sum _{i=M+1}^D(x_n^T{u}_i-{\bar{x}}^T{u}_i{)}^2\end{array}$$
代入得
$$\begin{array}{rl}J& =\frac{1}{N}\sum _{n=1}^N||x_n-{\tilde{x}}_n|{|}^2\\ & =\frac{1}{N}\sum _{n=1}^N\sum _{i=M+1}^D(x_n^T{u}_i-{\bar{x}}^T{u}_i{)}^2=\sum _{i=M+1}^D{u}_i^{T}S{u}_i\end{array}$$
而$S{u}_i={\lambda }_i{u}_i$，故
$$J=\sum _{i=M+1}^D{\lambda }_i$$
最小化$J$即选择$D-M$个最小特征值对应的特征向量，这实则与最大化方差形式等价。

往年试题

分享了一些往年试题的博客链接，不保证试题的真实性，仅供参考。
哈工大2020秋机器学习期末试题
哈工大2019秋机器学习期末试题

哈工大机器学习复习笔记（一）
哈工大机器学习复习笔记（二）
哈工大机器学习复习笔记（三）
哈工大机器学习复习笔记（四）