手写数字彩色图像识别-Keras实现(基于R语言)
本文摘自《Keras深度学习:入门、实战及进阶》一书。
本小节我们将利用MNIST数据集的训练数据训练模型,MNIST数据集的测试数据评估模型,再利用训练好的模型对本地的50个手写数字图像进行预测,查看预测效果。
在num文件夹中已经保存了50张0~9的彩色数字图像

使用EBImage包的readImage()函数将num文件夹中的所有数字图像读取到R中。
> library(keras)
> library(EBImage)
> # 图像数据读取
> setwd('../num') # 设置num文件夹为默认路径
> temp <- paste(1:50,'png',sep = '.')
> mypic <- list()
> for (i in 1:length(temp)) {mypic[[i]] <- readImage(temp[[i]])}
利用for循环语句,已经将50张数字图像读入到R中。利用plot()函数查看读取的数字图像。
> # 绘制数字图像
> par(mfrow=c(10,5))
> for(i in 1:50) plot(mypic[[i]])
> par(mfrow=c(1,1))

在对数据图像处理前,让我们先查看各个图像的维度大小。以下程序将每张图像的实际值和三个维度的实际大小保存到size对象中,并查看前六张图像的数据情况。
> # 查看各图像的维度大小
> size <- data.frame(pic = 1:50,
+ num = rep(0:9,each = 5),
+ dim1 = sapply(mypic,dim)[1,],
+ dim2 = sapply(mypic,dim)[2,],
+ dim3 = sapply(mypic,dim)[3,])
> head(size)
pic num dim1 dim2 dim3
1 1 0 122 106 3
2 2 0 119 106 3
3 3 0 126 100 3
4 4 0 125 115 3
5 5 0 124 118 3
6 6 1 100 108 3
数据框size中的dim1、dim2、dim3分别对应图像的像素宽度、像素高度和颜色通道。因为dim3列的值均为3,所以这些数字图像均为彩色图像,需利用colorMode()函数将它们转变为灰色图像。因为各图像的dim1和dim2值不相同,故这些图像大小不一致,需利用resize()函数进行处理。
> # 图像处理
> for (i in 1:length(temp)) {colorMode(mypic[[i]]) <- Grayscale} # 转换为灰色图像
> for (i in 1:length(temp)) {mypic[[i]] <- 1-mypic[[i]]} # 转换为背景色为黑色,数字为白色的图像
> for (i in 1:length(temp)) {mypic[[i]] <- resize(mypic[[i]], 28, 28)} # 将图像转换为28*28大小
> for (i in 1:length(temp)) {mypic[[i]] <- array_reshape(mypic[[i]], c(28,28,3))} # 将image转变为list
> new <- NULL
> for (i in 1:length(temp)) {new <- rbind(new, mypic[[i]])}
> newx <- new[,1:784] # 得到50*784的X二维矩阵
> newy <- size$num # 得到每个图像的实际数字
最后,再次使用plot()函数查看经过处理后的数字图像。
> # 绘制处理后的数字图像
> par(mfrow=c(5,10))
> for(i in 1:50) plot(as.raster(array_reshape(newx[i,],c(28,28))))
> par(mfrow=c(1,1))
> # 加载MNIST数据集
> mnist <- dataset_mnist()
> trainx <- mnist$train$x
> trainy <- mnist$train$y
> testx <- mnist$test$x
> testy <- mnist$test$y
> # 改变数据形状和大小
> trainx <- array_reshape(trainx, c(nrow(trainx), 784))
> testx <- array_reshape(testx, c(nrow(testx), 784))
> trainx <- trainx / 255
> testx <- testx /255
> # 独热编码
> trainy <- to_categorical(trainy, 10)
> testy <- to_categorical(testy, 10)
以下是深度学习建模代码。
> # 构建MLP模型函数
> build_model <- function() {
+ model <- keras_model_sequential() %>%
+ layer_dense(units = 512, activation = 'relu', input_shape = c(784)) %>%
+ layer_dropout(rate = 0.4) %>%
+ layer_dense(units= 256, activation = 'relu') %>%
+ layer_dropout(rate = 0.3) %>%
+ layer_dense(units = 10, activation = 'softmax')
+ # 编译
+ model %>% compile(
+ loss = 'categorical_crossentropy',
+ optimizer = optimizer_rmsprop(),
+ metrics = 'accuracy')
+ model
+ }
以下是训练模型代码。
> model <- build_model()
> history <- model %>% fit(
+ trainx,
+ trainy,
+ epochs = 30,
+ batch_size = 32,
+ validation_split = 0.2)
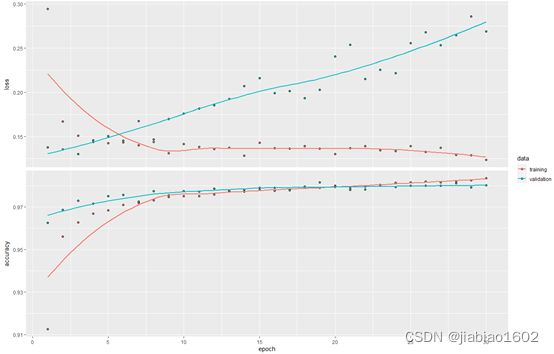
> plot(history)
> # 模型预测
> pred <- model %>% predict_classes(newx)
> t <- table(Actual = newy,Predicted = pred)
> t
Actual 0 1 2 3 4 5 6 7 8 9
0 4 0 1 0 0 0 0 0 0 0
1 0 5 0 0 0 0 0 0 0 0
2 0 0 5 0 0 0 0 0 0 0
3 0 0 1 4 0 0 0 0 0 0
4 0 1 1 0 2 0 0 0 0 1
5 0 0 0 0 0 4 0 0 1 0
6 0 0 0 0 0 4 1 0 0 0
7 0 0 1 1 0 0 0 2 1 0
8 0 0 3 1 0 0 0 0 0 1
9 0 0 0 1 1 1 2 0 0 0
从混淆矩阵可知,除了1、2这两种数字图像全部预测正确外,其他数字图像均有预测结果与实际值不一致情况。
通过以下程序代码绘制预测与实际不一致的数字图像。
> ind <- which(newy!=pred) # 提取预测与实际不一致的下标集
> par(mfrow=c(4,6))
> for(i in ind){
+ plot(as.raster(array_reshape(newx[i,],c(28,28))))
+ title(paste('Actual=',newy[i],'Predicted=',pred[i]))
+ }
> par(mfrow=c(1,1))