Coursera自动驾驶课程第9讲:Visual Features Detection Description and Matching
在上一讲《Coursera自动驾驶课程第8讲:Basics of 3D Computer Vision》中我们学习了计算机视觉基本知识。
本讲我们将学习计算机视觉中的视觉特征模块。
B站视频链接:https://www.bilibili.com/video/BV1PE411D72p
文章目录
-
-
- 1. Introduction to Image features and Feature Detectors
-
- 1.1 Overview
- 1.2 Points of Interest
- 1.3 Feature Extraction
- 2. Image Feature Descriptors
-
- 2.1 Feature Descriptors
- 2.2 Designing Invariant Descriptors: SIFT (重点)
- 3. Feature Matching (重点)
-
- 3.1 Overview
- 3.2 Distance Function
- 3.3 Brute Force Feature Matching
- 4. Handing Ambiguity in Matching
-
- 4.1 Overview
- 4.2 Distance Ratio
- 4.3 Updated Feature Matching
- 5. Outlier Rejection
-
- 5.1 Image Features: Localization
- 5.2 Random Sample Consensus (RANSAC)
- 5.3 Image Features: Localization (Updated)
- 6. Visual Odometry
-
- 6.1 Overview
- 6.2 Problem Formulation
- 6.3 Visual Odometry (重点)
-
1. Introduction to Image features and Feature Detectors
1.1 Overview
视觉特征可用于跟踪目标的运动并识别目标在地图中的位置。 本讲将会介绍如何通过一系列图像来检测和跟踪特征,以及如何与其他来源融合以进行定位。
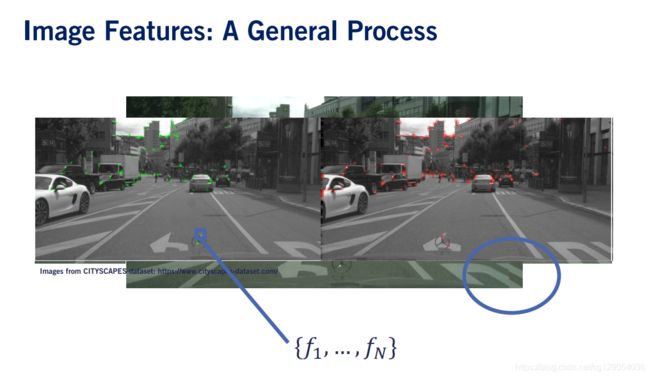
我们以一个实际的应用程序来开始,即图像拼接来描述此过程。 我们从两个不同的相机获得了两张图像,我们希望将它们缝合在一起以形成全景。
1.2 Points of Interest
我们开始定义图像特征的真正含义。特征是图像中的兴趣点。兴趣点通常有以下特征:
- 独特的,可识别的,并且与邻区域所不同。
- 可重复的。这意味着我们应该能够从同一场景的两个独立图像中提取相同的特征。
- 局部的。这意味着,如果远离紧邻区域的图像区域发生变化,则要素不应改变。
- 特征应该在图像中丰富。这是因为许多应用需要最少数量的独特点才能有效执行。
- 最后,生成特征不需要大量的计算。
 |
 |
1.3 Feature Extraction
如左图所示,在进行特征提取时往往有几点是需要考虑的。
重复纹理较少的地方往往很难定位。- 具有
较大对比度变化的色块(在渐变较大的地方)更容易定位,但是沿特定图像边缘的色块可能仍然令人困惑。例如,同一车道标记边缘上的两个红色矩形看起来非常相似。同样,这些位置具有挑战性,很难用作特征。 - 定位图像的最简单概念是角落。
当在至少两个明显不同的方向上的梯度较大时,会出现拐角。角落的示例以红色矩形显示。
现在我们来看看常用的特征检测算法:
- 最著名的检测算法是
哈里斯拐角检测器,它使用图像梯度信息来识别在 x x x和 y y y方向上强度变化很大的像素。但是,Harris拐角检测器检测到的拐角不是比例不变的,这意味着拐角的外观可能会有所不同,具体取决于相机与生成拐角的对象的距离。为了解决这个问题,研究人员提出了Harris-Laplace角检测器。 Harris-Laplace检测器可检测不同比例的拐角,并根据图像的拉普拉斯算子选择最佳比例。- 此外,研究人员还能够通过机器学习角点。快速角检测器是一种杰出的算法,由于其非常高的计算效率和可靠的检测性能,因此是最常用的特征检测器之一。
- 还有例如高斯的拉普拉斯算子检测器等。我们在这里不会深入讨论这些检测器,因为它们代表了正在进行研究的复杂领域,但是我们可以轻松地使用各种特征提取器。多亏了像OpenCV这样强大的开源实现。
现在,让我们看看这些检测器的一些示例。在这里,您可以看到哈里斯角落探测器检测到的角落。
这些功能主要捕获预期的拐角,在此可见强烈的照明变化。在这里,您可以在同一张图片上看到Harris-Laplace特征。通过使用拉普拉斯算子来确定比例,我们可以检测变角,这些变角在车辆相对于场景移动时更容易匹配。比例尺是通过每个要素周围的圆圈大小来表示的。圆圈越大,该要素的比例越大。
 |
 |
 |
 |
2. Image Feature Descriptors
2.1 Feature Descriptors
让我们开始定义什么是特征描述符。在数学上,我们通过特征点在图像中的坐标 u u u和 v v v来定义。我们将描述符 f f f描述为与每个特征相关的 n n n维向量。描述符的任务是在特征本身附近提供图像信息的summaty,可以采用多种形式。
与特征检测器的设计相似,我们还具有描述符设计所需的一些有利特征,以实现可靠的特征匹配。
- 与特征检测器一样,描述符应该是
可重复的,这意味着无论位置,比例和照明如何变化,两个图像中相同的兴趣点都应具有大致相同的描述符。 - 特征描述符的第二个重要特征是
独特性。 - 最后,描述符应该紧凑且有效地进行计算。这是因为我们通常需要对自动驾驶应用程序进行实时匹配。
 |
 |
 |
2.2 Designing Invariant Descriptors: SIFT (重点)
已经开发出多种有效的描述符用于特征匹配。因此,让我们看一下有关单个特征描述符设计的案例,以使您对描述符的工作有所了解。我们将描述如何计算由David Lowe在1999年专门设计的变速SIFT描述符。计算过程如下:
给定图像中的特征,移位描述符在其周围占据16 x 16像素的窗口,我们将此窗口称为特征局部邻域。- 然后,我们将此窗口分为
四个4×4单元格,以便每个单元格包含16个像素。 - 接下来,我们使用
梯度滤波器,计算每个像素的边缘和边缘方向。 - 为了使描述符稳定,我们
使用预定义的阈值抑制了弱边缘,因为它们的方向可能会发生很大变化,而图像之间的噪声很小。 - 最后,我们为每个单元格计算方向的32维直方图。并将所有四个单元格的直方图连接起来,以获得针对当前特征的最终128维直方图,我们称此直方图为描述符。
SIFT是人为设计的特征描述符的一个示例,并且在许多最新系统中使用。通常会在多个比例和方向上进行计算,以获得更好的比例和旋转不变性。最后,当与尺度不变特征检测器(例如高斯检测器的差)结合使用时,它会生成高度健壮的特征检测器和描述符对。
值得一提的是,关于特征检测器和描述符的文献很多。例如,SURF描述使用与SIFT类似的概念,但计算速度明显更快。文献中还存在许多其他变体,包括GLOH描述符,BRIEF和ORB描述符。
这里有很多首字母缩写词要记住,但是不用担心,我们不希望您记住所有这些。但是您可以在可用于开源计算机视觉库的实现中看到它们。现在,我们已经完成了关于特征检测器和描述符的讨论。尽管讨论的大多数算法都具有开源实现,但SIFT和SURF之类的专利已获得专利,未经作者批准,不得在商业上使用。
 |
 |
 |
3. Feature Matching (重点)
3.1 Overview
这里有一个特征匹配问题的例子。 给定一个特征及其在图像1中的描述符,我们想尝试在图像2中找到该特征的最佳匹配。 那么如何解决这个问题呢? 匹配问题的最简单解决方案称为暴力特征匹配,描述如下。
- 首先,定义
距离函数d d d,该距离函数比较两个特征 f i f_i fi和 f j f_j fj的描述符,并定义二者之间的距离。 两个描述符彼此之间越相似,则它们之间的距离越小。 - 其次,对于图像1中的每个特征 f i f_i fi,我们应用距离函数 d d d来计算图像2中每个特征 f j f_j fj的
距离。 - 最后,我们将返回图像2中称为 f c f_c fc的特征,并将其与图像1中特征 f i f_i fi的最小距离作为匹配。

3.2 Distance Function
下面介绍一些常见的距离函数:
- 用于比较描述符的最常见距离函数是
平方和(SSD)。 平方项惩罚两个描述符之间的变化,使其对描述符中的大变化敏感,但对较小的变化不敏感。 - 其他距离函数(如
绝对差(SAD))也是可行的替代方法, 绝对差之和等于均等地惩罚所有变化。 Hamming Distance用于二进制特征,对此所有描述符元素都是二进制值。

3.3 Brute Force Feature Matching
下面我们看几个特征匹配的例子,第一种情况,看看我们的暴力匹配器在实际中是如何工作的。考虑黄色边框内的特征。
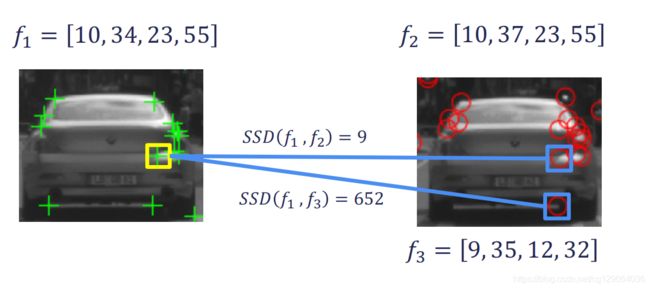
为简单起见,此功能具有一个二维描述符,我们将其称为 f 1 f_1 f1。让我们计算 f 1 f_1 f1和图像2中第一个特征之间的距离,我们将其标记为 f 2 f_2 f2。得到的SSD值为9。然后,我们计算 f 1 f_1 f1和图像2中第二个特征之间的距离,我们将其标记为 f 3 f_3 f3。在这里,我们得到的SSD值为652。现在,我们可以对第二张图像中的所有其他特征重复此过程,最终我们选择特征 f 2 f_2 f2作为我们的匹配项,因为它与 f 1 f_1 f1的距离最小。
现在,让我们考虑第二种情况,即特征检测器尝试匹配图像一中的特征,而在图像二中没有相应的特征。让我们看看当特征检测器遇到这种情况时,暴力方法会做什么。按照与之前相同的步骤,我们在图像1中特征 f 1 f_1 f1的描述符和图像2中所有特征的描述符之间计算SSD。得出 f 2 f_2 f2的得分最低。虽然为441,它仍然与原始图像中的 f 1 f_1 f1特征描述符完全不同。最终 f 2 f_2 f2为我们的最佳匹配。显然,这是不正确的。因为特征 f 1 f_1 f1与场景中的特征 f 2 f_2 f2不是相同的兴趣点。那么如何解决这个问题呢?我们可以通过设置距离阈值 δ \delta δ来解决此问题。这意味着,即使图像2中任何特征距 f 1 f_1 f1的距离都大于 δ \delta δ,也不会被视为匹配。
 |
 |
现在,让我们用阈值更新蛮力匹配算法。我们通常根据经验定义 δ \delta δ,它取决于应用程序和所使用的描述符。再次,我们定义距离函数以量化两个特征描述符的相似性。我们为可接受的匹配设置了最大距离阈值 δ \delta δ。然后,对于图像1中的每个特征,我们计算到图像2中每个特征的距离,并将最短距离作为最可能的匹配项。
当我们要匹配的特征数量较少时,暴力匹配是可行的。当特征数量增大时,使用特殊数据结构(例如k-d树)来加速匹配。不过好在OpenCV都已经提供了其实现。
4. Handing Ambiguity in Matching
4.1 Overview
我们先回顾几个特征匹配的例子。第一种情况下,我们有一个有效的特征 f 1 f_1 f1,第二个图片中匹配的特征为 f 2 f_2 f2。
第二种情况,在图像2中无法找到与图像1中相匹配地描述符。在这种情况下,我们使用`阈修改了暴力匹配算法,以消除不正确的匹配。由于特征和图像两者的距离都大于距离阈值 δ \delta δ,因此暴力匹配器将特征 f 2 f_2 f2和 f 3 f_3 f3都拒绝为潜在匹配,并且不返回任何匹配。
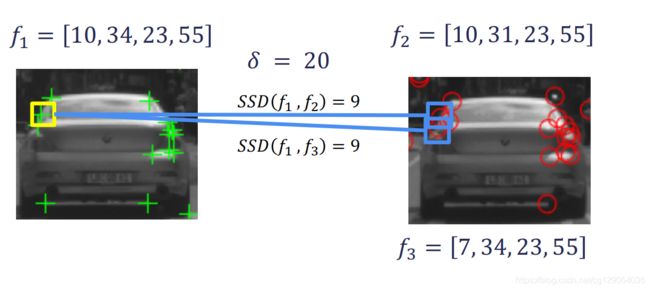
但是,让我们考虑第三种情况,我们再次尝试将图像1中的特征 f 1 f_1 f1与图像2中的对应特征进行匹配。利用此处提供的特征向量,特征 f 1 f_1 f1与特征$f_2$2的SSD值为9。另一个特征f3,SSD值仍为9。这两个特征都具有小于 δ \delta δ的SSD(在这种情况下为20),两者都是有效的匹配。我们该怎么办呢?
 |
 |
 |
4.2 Distance Ratio
对第三种情况,我们将特征 f i f_i fi称为具有模糊匹配的特征。 David Lowe在1999年提出了一个解决该问题的精巧解决方案。解决方案如下。
- 首先,我们计算特征 f i f_i fi与图像2中的所有特征 f j f_j fj之间的距离。
- 我们选择图像2中的特征 f c f_c fc,为与特征 f i f_i fi为最接近的匹配特征。
- 然后,我们继续选取特征 f s f_s fs,即与 f i f_i fi第二接近的特征。
- 最后,我们发现最接近的匹配 f c f_c fc比我们的第二接近的匹配 f s f_s fs接近多少。这可以通过
距离比来完成,其公式为:
0 ≤ d ( f i , f c ) d ( f i , f s ) ≤ 1 0 \leq \frac{d\left(f_{i}, f_{c}\right)}{d\left(f_{i}, f_{s}\right)} \leq 1 0≤d(fi,fs)d(fi,fc)≤1
如果距离比接近于1,则意味着根据我们的描述符和距离函数, f i f_i fi匹配 f s f_s fs和 f c f_c fc。在这种情况下,我们不想在以后的处理中使用此匹配项,因为我们的匹配器显然不知道图像2中的哪个位置对应于图像1中的特征。

4.3 Updated Feature Matching
让我们用距离比公式更新暴力匹配算法。
将距离替换为距离比,作为我们保持匹配的指标。 通常,我们将距离比阈值设置为0.5左右,这意味着我们要求最佳匹配至少要比初始特征描述符的第二最佳匹配接近两倍。

5. Outlier Rejection
5.1 Image Features: Localization
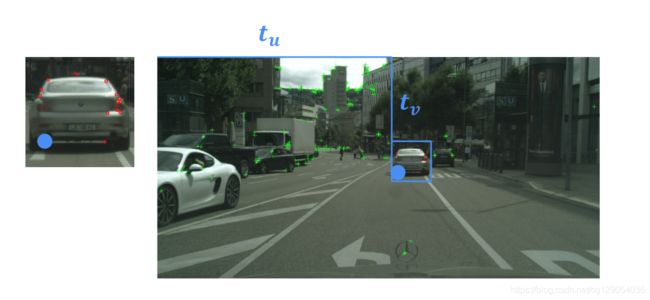
定位问题定义如下:从不同的角度给出同一场景的任意两个图像,找到第一幅图像的坐标系(以红色显示)和第二幅图像的绿色系之间的平移T。 要解决此定位问题,我们需要执行以下步骤。
- 首先,我们需要找到图像1在图像2的 u u u图像轴上的位移。 我们称这个位移为 t u t_u tu。
- 其次,我们需要在图像2的 v v v轴上找到图像1的位移,我们将其称为位移 t v t_v tv。
- 最后求解最能使这些匹配特征对齐的
位移。
 |
 |
我们首先从图像1和图像2中计算特征及其描述符开始。首先,让我们根据匹配特征从数学上定义问题的解决方案。
我们将图像1和图像2中的特征对表示为 f i ( 1 ) f^{(1)}_i fi(1)和 f i ( 2 ) f^{(2)}_i fi(2)。其中 i i i介于0和 N N N之间,即我们的匹配算法返回的特征对总数。特征对中的每个特征均由其像素坐标 u i u_i ui和 v i v_i vi表示。请注意,在应用平移之后,图像中的每个像素应与图像2中的相应像素重合。然后,我们可以使用特征对转换进行建模,转换公式为:
u i ( 1 ) + t u = u i ( 2 ) v i ( 1 ) + t v = v i ( 2 ) u_{i}^{(1)}+t_{u}=u_{i}^{(2)} \\v_{i}^{(1)}+t_{v}=v_{i}^{(2)} ui(1)+tu=ui(2)vi(1)+tv=vi(2)
通过模型参数 t u t_u tu和 t v t_v tv将图像1平移到图像2中的相应位置。这里,所有特征的平移都是相同的,我们假设刚体运动。
然后使用最小二乘估计。最小二乘求解是 t u t_u tu和 t v t_v tv的值,该值最小化所有像素对之间的平方误差之和。现在我们已经定义了定位问题。
 |
 |
让我们返回特征匹配的结果。通过视觉观察特征位置,可以看到紫色圆圈中的特征对实际上是不正确的匹配。即使使用距离比方法,也会发生这种情况,这在特征匹配中很常见。我们称此类特征对为离群值(outlier)。

5.2 Random Sample Consensus (RANSAC)
让我们看看是否可以识别这些离群值,并避免在最小二乘求解中使用它们。可以使用称为RANSAC的基于模型的异常值排除方法来处理异常值。由Martin Fischler和Robert Bolles于1981年开发。
RANSAC算法的过程如下:
- 首先,给定一个用于从一组数据点中识别问题解决方案的模型,找到计算该模型的参数所需的最小数量的数据点或样本。在我们的案例中,模型参数是最小二乘解的 t u t_u tu和 t v t_v tv。
- 其次,从数据中随机选择 M M M个样本。
- 第三,仅使用从数据集中选择的 M M M个样本来计算模型参数。
- 第四,使用计算出的参数并计算剩余多少数据点与此计算出的解决方案相符。并将其称为
内部值。 - 第五,如果 C C C大于内部阈值,或者算法已迭代超过预设的最大迭代数,则终止并返回计算出的解和内线集。否则,返回第二步并重复。
- 最后,重新计算并从最佳内部值集返回模型参数。

5.3 Image Features: Localization (Updated)
要估计 t u t_u tu和 t v t_v tv,我们需要一对特征。现在,让我们通过RANSAC算法来解决这个问题。
-
首先,我们从匹配的样本中随机选择一个特征对。
-
现在,我们需要使用计算出的特征对来估计模型。使用特征对,我们计算沿 u u u图像轴的位移 t u t_u tu和沿 v v v图像轴的位移 t v t_v tv。
现在,我们需要通过计算内部数来检查我们的模型是否有效。在这里,我们使用公差来确定内部值,因为我们不太可能以100%的精度满足模型。不幸的是,我们的第一次迭代选择了较差的特征匹配来计算模型参数。当使用该模型计算图像一中有多少特征转换为图像二中它们的匹配位置时,我们注意到它们都没有。由于我们的内部数为零,因此我们返回并随机选择另一个特征对,然后重新启动RANSAC流程。
 |
 |
 |
我们使用新的随机采样特征对来获得新的模型参数。这次我们选择两个特征来计算模型参数, 这次我们可以看到大多数特征实际上都适合此模型。 实际上,在12个特征中有11个被视为内部特征。 由于我们的大多数功能都是inliers,因此我们对此模型感到满意,并且可以停止RANSAC算法。
使用特征匹配时,离群值移除是提高鲁棒性的关键过程,并且可以大大提高定位结果的质量。
 |
 |
 |
6. Visual Odometry
6.1 Overview
视觉里程计可以定义为通过检查车载摄像机图像上的运动变化来逐步估计车辆姿态的过程。
下面是视觉里程计的优势:
- 视觉里程计不会受车轮打滑地影响。
- 并且与车轮里程计相比,能够产生更准确的轨迹。这是因为可从图像获得更多信息。但是,我们通常无法从单个摄像机估计绝对姿态。这意味着需要通过调整两个图像之间的相对运动估算。
因此我们就得到了视觉里程计的劣势:
- 通常我们需要至少一个附加地传感器,如第二个摄像头或惯性测量单元,以便在使用VO时能够提供精确缩放的轨迹。
- 此外,摄像机对极端的光照变化敏感,因此很难在夜间以及有前灯和路灯的情况下进行VO。
- 最后,从其他里程计估计机制可以看出,随着VO估计误差的累积,来自VO的姿态估计将始终随时间漂移。因此,我们经常将VO性能表示为单位行驶距离的百分比误差。

6.2 Problem Formulation
让我们以数学方式定义视觉里程计问题。 给定两个连续的图像帧 I k − 1 I_{k-1} Ik−1和 I k I_k Ik,我们想估计由平移 T T T和两个帧之间的旋转 R R R定义的变换矩阵 T k T_k Tk。
当我们有连续的 m m m帧图像时,我们能够恢复相机的全部轨迹,由于相机被固定在自动驾驶汽车上,这也代表了车辆轨迹的估计。

6.3 Visual Odometry (重点)
现在,我们来描述视觉里程计处理的一般过程。 给定两个连续的图像帧, I k I_k Ik和 I k − 1 I_{k-1} Ik−1,我们想估计这两个帧之间的变换 T k T_k Tk。
- 首先,我们进行
特征检测和描述。 我们最终得到一组特征 f k f_k fk和 f k − 1 f_{k-1} fk−1,然后,我们进行特征匹配。 - 之后,我们使用匹配的特征来估计由变换 T k T_k Tk表示的两个摄像机帧之间的运动。
- 最后,我们扩展到多个帧进行定位优化。

运动估计是VO中最重要的一步,它将成为本课程的主题。我们执行运动估计步骤的方式取决于我们拥有哪种类型的特征表示。
- 在 2 D − 2 D 2D-2D 2D−2D运动估计中,两个帧中的特征匹配仅在图像坐标中描述。这种视觉测距法非常适合跟踪图像框中的对象。例如,这对于摄像中的视觉跟踪非常有用。
- 在 3 D − 3 D 3D-3D 3D−3D运动估计中,特征匹配在世界3D坐标系中描述。这种方法需要能够在 3 D 3D 3D空间中定位新的图像特征,因此与深度相机,立体相机和其他可提供深度信息的多相机配置一起使用。
- 3 D − 2 D 3D-2D 3D−2D运动估计,其中在 3 D 3D 3D世界坐标中特征为 f k − 1 f_{k-1} fk−1,而在图像坐标中指定对应投影为 f k f_k fk。
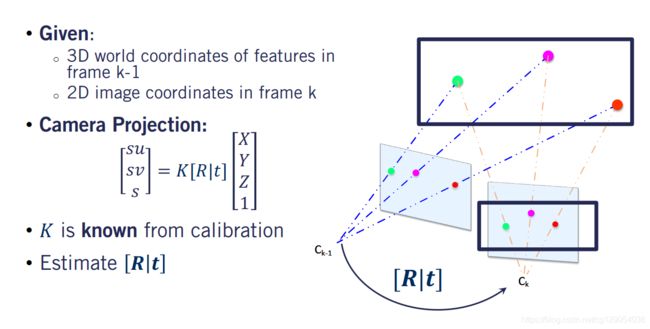
下面介绍 3 D − 2 D 3D-2D 3D−2D运动估计的方法。已知在 k − 1 k-1 k−1帧中图像特征和其对应 3 D 3D 3D坐标,通过特征匹配,我们还可以在新帧 k k k中获得相同特征的 2 D 2D 2D图像坐标。
我们希望使用此信息来估计两个相机帧之间的旋转矩阵 R R R和平移矢量 t t t。这会让您想起我们以前学到的东西吗?如果您正在考虑相机标定,那是正确的。实际上,我们也使用与在视觉里程计中进行标定所使用的投影几何方程式相同的方法。标定和VO之间要注意的简化区别是,照相机固有内参矩阵k是已知的。因此,我们不必再次解决它。现在,我们的问题简化为使用所有匹配特征构建的方程组对变换分量 R R R和 t t t进行估计。
 |
 |
求解旋转矩阵和平移向量的一种常用算法是PNP算法。给定 3 D 3D 3D中的特征位置,中其对应的 2 D 2D 2D投影以及相机固有标定矩阵 k k k,PnP算法处理流程如下:
- 首先,PnP使用
直接线性变换来求解 R R R和 t t t的初始值。用于估计 R R R和 t t t的DLT方法需要一个线性模型,并构建一组线性方程式,以使用诸如SVD进行求解。 - 在下一步中,我们将使用
迭代非线性优化技术(例如Luvenburg Marquardt方法)来优化我们的解决方案。 - PnP算法
至少需要三个特征点才能求解 R R R和 t t t。当仅使用三个特征时,将得出四个可能的解决方案,因此,将使用第四个特征点来确定哪个解决方案最有效。 - 最后,通过假设PnP在四个点上求解的结果是我们想要的,可以将RANSAC算法合并到PnP中。然后,我们选择所有特征匹配的子集来评估该模型,并计算内在点百分比以确认所选点匹配的有效性。
实现VO算法时,还有许多有趣的细节需要考虑。幸运的是,PnP算法在OpenCV中已经得到实现了。实际上,OpenCV甚至包含一个带有RANSAC的PnP版本,以实现异常排除。
 |
 |