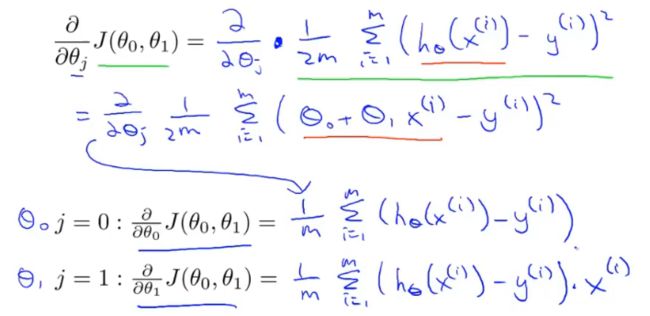机器学习笔记
监督学习
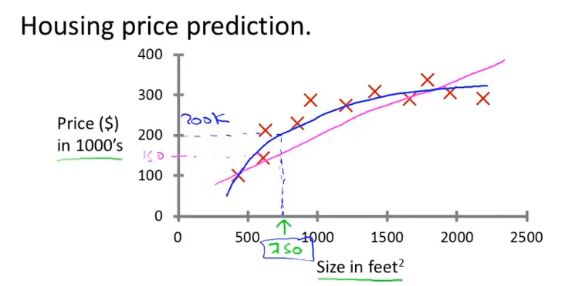
监督学习是已经知道数据的label,例如预测房价问题,给出了房子的面积和价格
回归问题是预测连续值的输出,例如预测房价。
分类问题是预测离散值输出,例如判断肿瘤是良性还是恶性
无监督学习
无监督学习是不知道数据具体的含义,比如给定一些数据但不知道它们具体的信息,对于分类问题无监督学习可以得到多个不同的聚类(聚类算法),从而实现预测的功能。
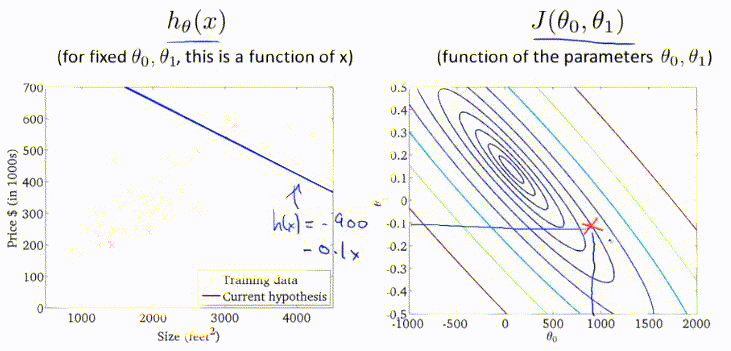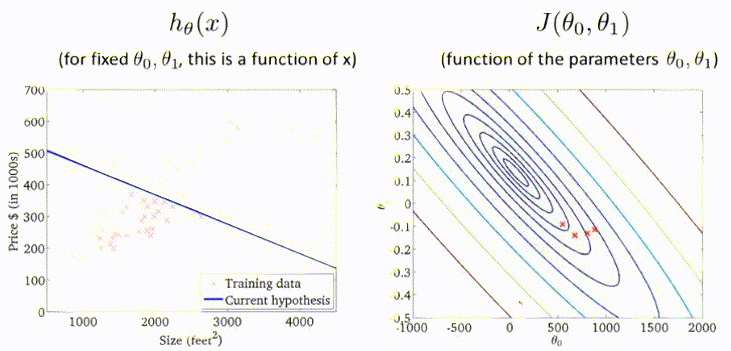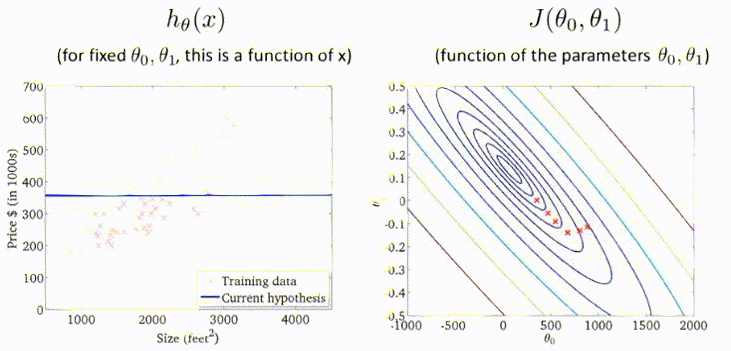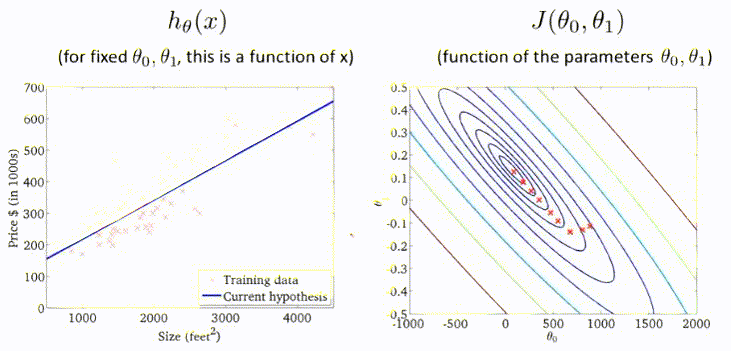
单变量线性回归(Linear Regression with One Variable)
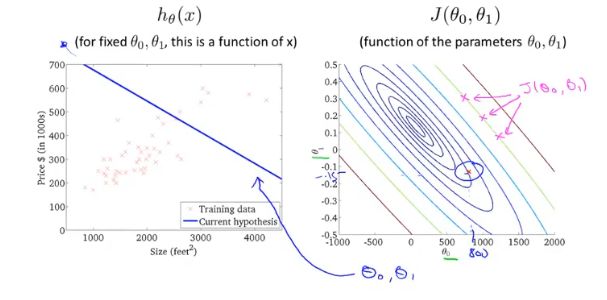
线性回归是拟合一条线,将训练数据尽可能分布到线上。另外还有多变量的线性回归称为多元线性回归。
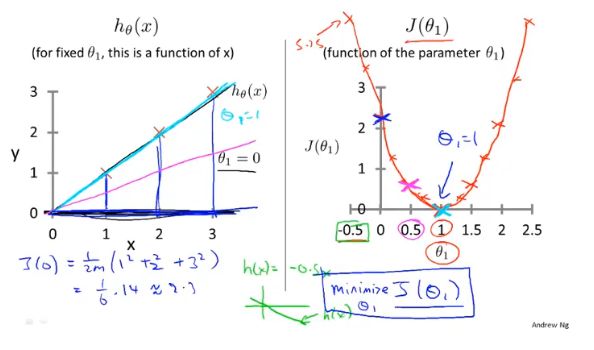
代价函数
cost function,一般使用最小均方差来评估参数的好坏。
梯度下降
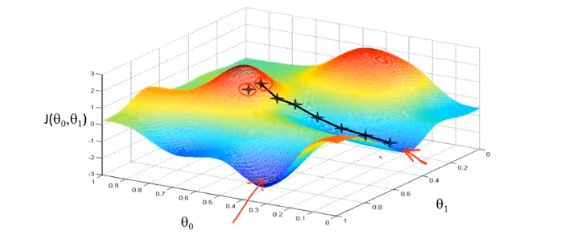
梯度下降,首先为每个参数赋一个初值,通过代价函数的梯度,然后不断地调整参数,最终得到一个局部最优解。初值的不同可能会得到两个不同的结果,即梯度下降不一定得到全局最优解
确定每次补偿,每次在通过微积分求导确定最大斜率及方向,进而确定下一个取值点
梯度下降在具体的执行时,每一次更新需要同时更新所有的参数。
梯度下降公式中有两个部分,偏导数和学习率
偏导数,用来计算当前参数对应代价函数的斜率,导数为正则θ减小,导数为负则θ增大,通过这样的方式可以使代价函数的函数值不断减小。
通过分别对θ0和θ1,分别求偏导,获得梯度下降最大的方向。同时获得更新后的θ0和θ1
α用来描述学习率,即每次参数更新的步长。α的大小不好确定,如果太小则需要很多步才能收敛,如果太大最后可能不会收敛甚至可能发散。
当θ处于局部最优解时,θ的值将不再更新,因为偏导为0。
这也说明了如果学习率α不改变,参数也可能收敛,假设偏导>0,因为偏导一直在向在减小,所以每次的步长也会慢慢减小,所以α不需要额外的减小。
单元梯度下降
梯度下降每次更新的都需要进行偏导计算,这个偏导对应线性回归的代价函数。即对代价函数分别求偏导。
对代价函数求导的结果为:
梯度下降的过程容易出现局部最优解:(函数复杂,多元,有多个极值点)
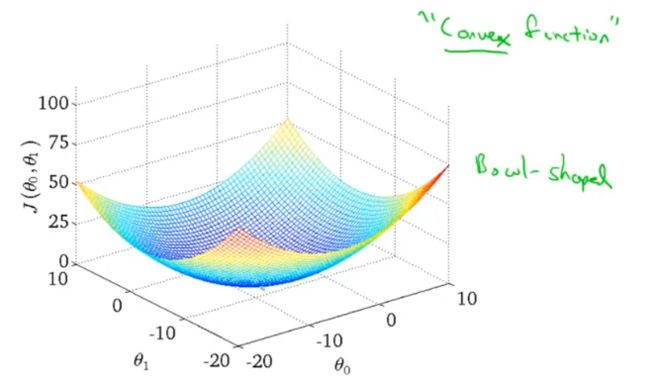
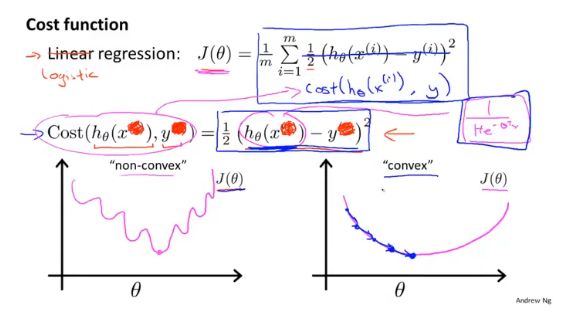
但是线性回归的代价函数,往往是一个凸函数(局部最优解即全局最优解)。它总能收敛到全局最优。
梯度下降过程的动图展示:
多元梯度下降
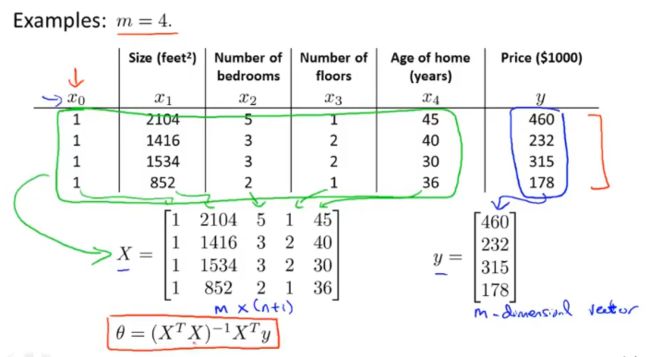
通常问题都会涉及到多个变量,例如房屋价格预测就包括,面积、房间个数、楼层、价格等
因此代价函数就不再只包含一个变量,为了统一可以对常量引入变量x0=1
每一个x是一个向量,是特征,含有多个属性(除x0=1,为常数)
虽然参数的个数增多,但是对每个参数求偏导时和单个参数类似
(仍然是分别对每个参数即特征求偏导)
Batch梯度下降
每一步梯度下降,都需要遍历整个训练集样本。
特征缩放
特征的特征值之间大小可能相差很多,进行计算距离如欧几里距离时,距离会被特征值大的特征主导,因此需要对特征进行特征缩放,即归一化或标准化
特征缩放也可以加快梯度收敛的速度
归一化(受异常值影响)
标准化
矩阵和向量
数学计算转化为矩阵形式,可以简化代码书写、提高效率、代码易理解
矩阵乘法不满足交换律:
矩阵乘法满足结合律:
单位矩阵:
矩阵的逆:
首先是方阵
不是所有的矩阵都有逆
转置矩阵:
正则方程
正则方程和梯度下降都是求最优解θ,使得代价函数最小
利用线性代数的方法直接求解θ
逻辑回归
Logistic Regression
逻辑回归用于解决分类的问题,如果使用线性回归可能会造成很大的误差;假如样本的标签值为0、1,线性回归输出值是连续的存在>1和小于0的情况,不符合实际。
如果对于一个均匀的数据,使用线性回归,选取0.5作为分界线,可能会得到一个比较准确的模型,但是如果数据不太均匀就会存在很大的误差。
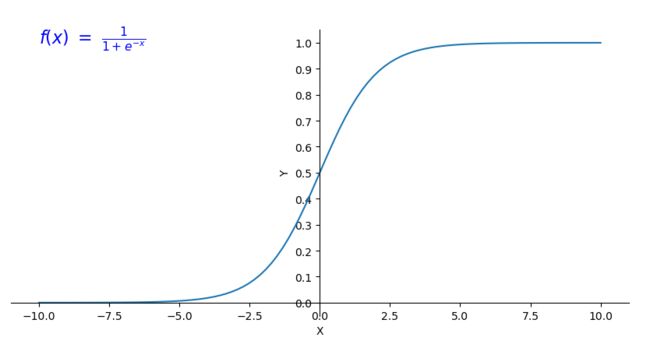
激活函数sigmoid
激活函数的y值分布在[0,1]内,对于分类问题,我们可以使用激活函数的值来表示满足特征的概率。
激活函数是在神经网络层间输入与输出之间的一种函数变换,目的是为了加入非线性因素,增强模型的表达能力。
决策界限(Dicision Boundary)
决策边界是假设函数(构造假设函数是为了寻找一条与数据拟合的直线)的一个属性,取决于函数的参数(θ),而不是数据集。
需要使用数据训练集确定参数(θ),确定参数进而确定决策边界,调整参数调整决策边界,提高模型预测精度。
决策边界为
代价函数(Cost Function)
逻辑回归一般使用对数函数作为代价函数:
首先对于分类函数来说,他的输出值范围为[0,1],得到的对数图像如下:
当评估模型参数对y=1(恶性肿瘤)进行预测的好坏时,如果实际为恶性,预测值也为1(恶性),此时的代价为0;如果实际为恶性,预测为0(良性),此时的代价为+∞,这时代价函数就很好的评估了参数θ的表现。
同样对于y=0(良性肿瘤)的代价函数为:
y的取值只有0、1,可以将上面两个函数合成一个,评估当前参数的J(θ)为:
梯度下降(Gradient Descent)
在确定代价函数之后的任务是,如何最小化代价函数,因为代价函数是凸的,所以可以使用梯度下降求解。
具体的偏导推导过程:
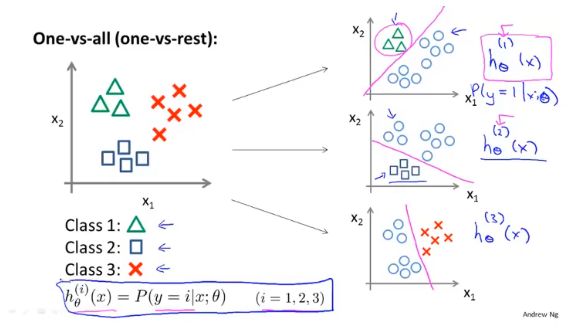
多元分类
对每个特征单独训练,在做预测的时候,取三个分类器结果最大的。
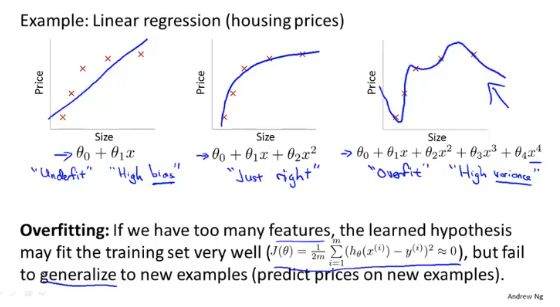
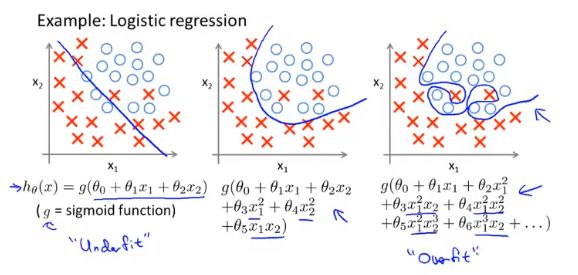
过拟合
存在多个特征,但是数据很少,或者模型函数不合理,都会出现过拟合的现象。过拟合可能对样本数能够很好的解释,但是无法正确的预测新数据。(对特征学习过强,无法泛化)
欠拟合:模型对特征学习不够,没有学习到特征的,考虑增加新的特征或者尝试非线性模型解决
正则化
Regularization
解决过拟合的方法:
正则化处理过拟合问题:
在代价函数中加入正则项,通过lambda的来平衡拟合程度和参数的大小,θ越大越容易出现过拟合的现象。
模型评估
训练、测试集
将数据集分为训练集和测试集,训练集得到参数θ,然后使用测试集的数据对参数θ\thetaθ进行评估,即计算误差。
线性回归问题的评估:
逻辑回归问题的评估:
训练、验证、测试集
首先用训练集得到一个最优的参数θ,然后用测试集进行评估误差。通过这样的方式可以在众多模型中选择一个理想的模型。
但是这样做并不能评估模型的泛化能力,通过测试集评估选择的模型,可能刚好适合测试集的数据,并不能说明它对其他数据的预测能力,这时就引入了验证集。
将数据集分为:训练集、验证集、测试集。
对于每个集合都可以计算相应的误差。
这样在选择模型的时候,可以先使用测试集得到每个模型的θ,然后使用验证集评估得到误差最小的模型,最后使用测试集评估他的泛化能力。
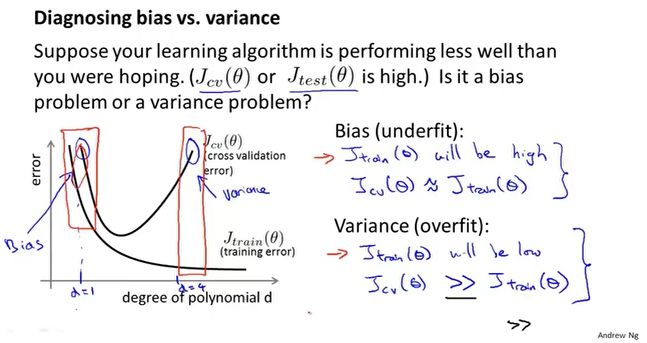
偏差、方差
当多项式次数增大时,训练集的误差慢慢减小,因为多项式次数越高,图像拟合的就越准确。但是验证集不同,它的趋势是先减少后增大,这分别对应着欠拟合和过拟合。
那么我们可以根据误差的不同表现来区分偏差和方差
高偏差:训练误差和验证误差都很大。(欠拟合)
高方差:训练误差小,验证误差大。(过拟合)
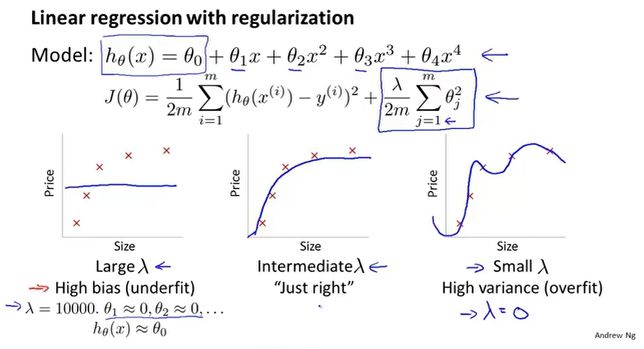
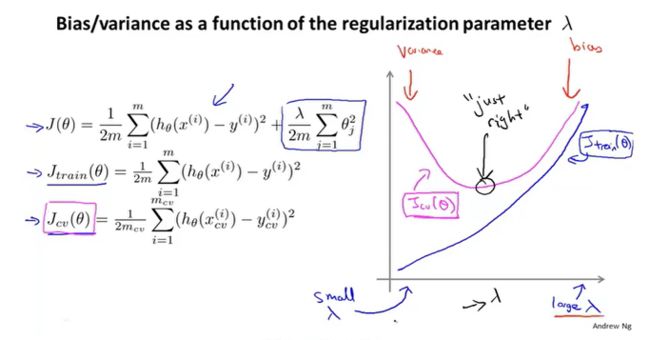
正则化
通过引入λ来平衡多形式的权重。
当λ太大,参数θ≈0,模型近似直线,即欠拟合。当λ太小,就会出现过拟合。
学习曲线
高偏差的模型的学习曲线:
高方差的特点是训练误差和验证误差之间有很大的差距,这时可以选择增加数据,随着图像右移可以看出训练误差和验证误差会慢慢接近。
如何抉择
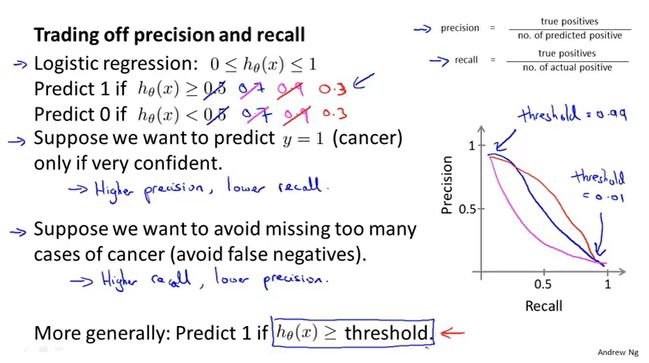
查准率、召回率
例如对癌症的预测,相对于样本数据真实得癌症的人非常少,大概只有0.5%的概率,这样的问题称为偏斜类,一个类中的样本数比另一个类多得多。
对于偏斜类的问题,如何评估模型的精准度呢?可能一个只输出y=1的函数都比你的模型准确。
这里引入了查准率和召回率,对于稀有的样本有:
通常如果阈值设置的比较高,那么对应的查准率高、召回率低;相反如果阈值设置的低,那么查准率低、召回率高。
F1 score
神经网络
大多数的机器学习所涉及到的特征非常多,对于非线性分类问题,往往需要构造多项式来表示数据之间的关系,多项式的组成方式千变万化,这对计算带来一定困扰。
大脑中的神经元结构:
机器学习中的神经网络一般包括三部分,输入层,隐藏层,输出层。
数据从输入层开始,通过激活函数前向传播到第一隐藏层,经过多个隐藏层,最后到达输出层,神经网络表示复杂的逻辑关系,主要是对隐藏层的构造。
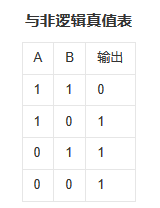
逻辑运算
OR或,AND与,XOR异或,NOR或非,NAND与非,XNOR异或非
XOR异或:相同为零,不同为一。
NOR或非:即作一次或者多次“或”运算后再做一次“非”运算.
NAND与非:即先作一次“与”运算后,再做一次“非”运算。
XNOR异或非:相同为一,不同为零。
如上为一个XNOR的分类问题,$xnor=(x_1 & x_2) or (\bar{x_1} & \bar{x_2})$,我们可以搭建出每种逻辑运算的神经网络,最终整合得到XNOR的神经网络模型。
AND运算
OR运算
NOT运算
XNOR运算