PID控制算法
PID
- 1. 什么是PID控制算法
-
- 1.0 棒棒控制(启停式控制)
- 1.1 KP比例参数的引入
- 1.2 KI积分参数的引入
- 1.3 KD微分参数的引入
- 2. 位置式PID
-
- 2.1 原理
- 2.2 C语言代码实现
- 3. 增量式PID
-
- 3.1 原理
- 3.2 C语言代码实现
- 4. 参数整定
-
- 4.1 PID手动整定
- 参考资料
1. 什么是PID控制算法
PID控制就是对偏差进行比例、积分、微分的计算从而去达到用户的期望目标的控制
由于3个单元组成:比例(P)单元、积分(I)单元、微分(D)单元。

U ( t ) = K p [ e ( t ) + 1 K i ∫ 0 t e ( t ) d t + K d d e ( t ) d t ] U(t) = Kp[e(t)+\frac1{Ki}\int_{0}^{t}e(t)dt+Kd\frac{de(t)}{dt}] U(t)=Kp[e(t)+Ki1∫0te(t)dt+Kddtde(t)]
-
u(t)为控制器输出的控制量;(输出)
-
e(t)为偏差信号,它等于给定量与输出量之差;(输入)
-
KP 为比例系数;(对应参数 P)
-
KI 为积分时间常数;(对应参数I)
-
KD 为微分时间常数。(对应参数 D)
(2022/3/20编辑)
1.0 棒棒控制(启停式控制)
若我想进行一个温度控制的时候,则对温度引入反馈调节,即:当温度小于目标温度的时候就加热,目标大于目标温度的时候就停止加热或者降温,这么做就是棒棒控制。
1.1 KP比例参数的引入
但是棒棒控制的缺陷在于,我不知道每次的加热和降温给多少会比较好,所以人们引入了比例项来对棒棒控制进行改进,即:当我加热接近到目标温度时候就减少加热量,这样引入了对误差*比例参数项,当误差减小的时候,输出也减小了。
U ( t ) = K P ∗ e ( t ) U(t)=KP*e(t) U(t)=KP∗e(t)
1.2 KI积分参数的引入
若仅有KP比例控制的缺陷是:无法达到目标温度,因为每次我接近目标温度之后,误差变为0,输出则为0,很快温度就又低下来了。(这种则称为静态误差)。
所以人们引入了积分项来对纯比例P控制进行改进。即:我一直累加你的误差,当我很接近目标误差趋向于0的时候,我的积分项可以把我的输出再抬一点抬上去,从而去弥补静态误差;
U ( t ) = K P ∗ e ( t ) + K I ∗ ∫ 0 t e ( t ) d t U(t)=KP*e(t)+KI*\int_0^t {e(t)}dt U(t)=KP∗e(t)+KI∗∫0te(t)dt
1.3 KD微分参数的引入
但是人们又发现PI控制的一些缺陷:曲线在目标直线附近一直在高频的小幅度波动,一段时间后才接近目标值,若参数不好可能还达不到目标值。
所以人们引入了微分项,去抑制这种振荡(波动)。
U ( t ) = K P ∗ e ( t ) + K I ∗ ∫ 0 t e ( t ) d t + K D d e ( t ) d t U(t)=KP*e(t)+KI*\int_0^t {e(t)}dt+KD\frac{de(t)}{dt} U(t)=KP∗e(t)+KI∗∫0te(t)dt+KDdtde(t)
(编辑结束)
离散化PID
因为采样数据是离散的,所以我们需要使用离散的差分方程代替连续的微分方程,来根据采样时刻的偏差值计算控制值
(1)用一阶差分代替一阶微分
(2)用累加代替积分
(编辑于2021/12/12)
为什么要用PID
- 在驱动电机给电机PWM波的时候,输出给电机的电压可能是不稳定的,具有尖峰,不够平滑,所以需要有PID(反馈增加稳定性)
- 同时由于电压的掉电也会影响速度;
(编辑结束)
2. 位置式PID
2.1 原理
U ( t ) = K p × e ( k ) + K i × ∑ e ( k ) + K d × [ e ( k ) − e ( k − 1 ) ] U(t)=Kp×e(k)+Ki×∑e(k)+Kd×[e(k)-e(k-1)] U(t)=Kp×e(k)+Ki×∑e(k)+Kd×[e(k)−e(k−1)]
- 比例P : e(k) 本次偏差(用户设定的值(目标值) - 控制对象的当前的状态值)
- 积分I : ∑e(i) 误差的累加(连续域上的积分对应离散的求和)
- 微分D : e(k) - e(k-1) 这次误差-上次误差(连续域上的微分对应差分)
- U(t):代表输出
目的:
位置式PID是当前系统的实际位置,与你想要达到的预期位置的偏差,进行PID控制
优点
- 直接赋值新的PWM调节更加灵敏
缺陷:
- Ki会不断的积累误差,一旦控制输出出错(控制对象的当前的状态值出现问题 ),u(k)的大幅变化会引起系统的大幅变化,所以在u(k)达到最大和最小时,要停止积分作用,并且要有积分限幅和输出限幅
- 所以在使用位置式PID时,一般我们直接使用PD控制
使用领域:
位置式 PID 适用于执行机构不带积分部件的对象,如舵机和平衡小车的直立和温控系统的控制
2.2 C语言代码实现
int Position_PID (int Encoder,int Target)
{
static float Bias,Pwm,Integral_bias,Last_Bias;
Bias=Encoder-Target; //计算偏差
Integral_bias+=Bias; //求出偏差的积分
Pwm=Position_KP*Bias+Position_KI*Integral_bias+Position_KD*(Bias-Last_Bias);
Last_Bias=Bias; //保存上一次偏差
return Pwm; //输出
}
- 一般在定时中断中执行,为了让它执行的频率是个定值,符合时序
3. 增量式PID
3.1 原理
▲ U ( t ) = K p [ e ( k ) − e ( k − 1 ) ] + K i ∗ e ( k ) + K d [ e ( k ) − 2 e ( k − 1 ) + e ( k − 2 ) ] ▲U(t)=Kp[e(k)-e(k-1)]+Ki*e(k)+Kd[e(k)-2e(k-1)+e(k-2)] ▲U(t)=Kp[e(k)−e(k−1)]+Ki∗e(k)+Kd[e(k)−2e(k−1)+e(k−2)]
- 比例P : e(k)-e(k-1) 这次误差-上次误差
- 积分I : e(i) 误差
- 微分D : e(k) - 2e(k-1)+e(k-2) 这次误差-2*上次误差+上上次误差
- ▲U(t):输出的增量,相当于对位置式进行了微分后返回的东西再积分
增量式PID根据公式可以很好地看出,一旦确定了 KP、TI 、TD,只要使用前后三次测量值的偏差, 即可由公式求出控制增量
而得出的控制量▲u(k)对应的是近几次位置误差的增量,而不是对应与实际位置的偏差没有误差累加
也就是说,增量式PID中不需要累加。控制增量Δu(k)的确定仅与最近3次的采样值有关,容易通过加权处理获得比较好的控制效果,并且在系统发生问题时,增量式不会严重影响系统的工作
缺点
- PWM会不断的积累,如果在我未开启电机驱动而开启了PID计算时输出的PWM会不断攀升
总结:增量型 PID,是对位置型 PID 取增量,这时控制器输出的是相邻两次采样时刻所计算的位置值之差,得到的结果是增量,即在上一次的控制量的基础上需要增加(负值意味减少)控制量。
3.2 C语言代码实现
int Incremental_PI (int Encoder,int Target)
{
static float Bias,Pwm,Last_bias;
Bias=Encoder-Target; //计算偏差
Pwm+=Velocity_KP*(Bias-Last_bias)+Velocity_KI*Bias; //增量式PI控制器计算公式
Last_bias=Bias; //保存上一次偏差
return Pwm; //增量输出
}
4. 参数整定
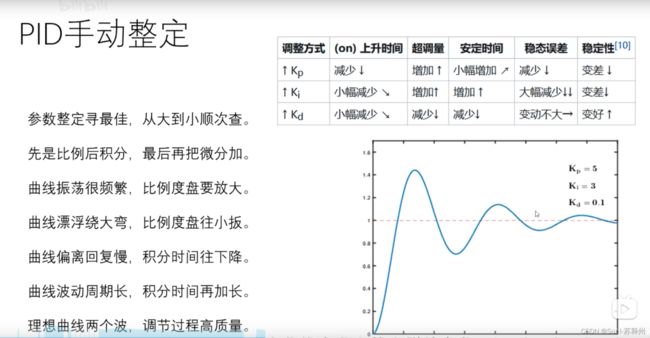
4.1 PID手动整定
参考资料
位置式PID与增量式PID区别浅析
十分钟入门PID控制器
带你认识PID闭环控制 - 增量式PID实现电机速度闭环