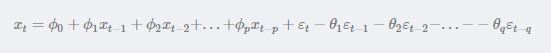CNN做时间序列预测_关于时间序列预测的一些总结

时间序列预测分析就是利用过去一段时间内某事件时间的特征来预测未来一段时间内该事件的特征。这是一类相对比较复杂的预测建模问题，和回归分析模型的预测不同，时间序列模型是依赖于事件发生的先后顺序的，同样大小的值改变顺序后输入模型产生的结果是不同的。首先需要明确一点的是，时间序列可以分为平稳序列，即存在某种周期，季节性及趋势的方差和均值不随时间变化的序列，及非平稳序列。

1.传统时序建模方法

传统预测方法可以分为两种，一种是更加传统的，如移动平均法，指数平均法等；一种是用的还算较多的，即AR,MA,ARMA等，下面主要介绍一下这三种方法，这类方法比较适用于小规模，单变量的预测，比如某门店的销量预测等：

（1）AR模型

具有如下结构的模型称为p阶自回归模型，简记为AR(p)：

随机变量Xt的取值Xt是前p期xt−1,xt−2,...,xt−pxt−1,xt−2,...,xt−p的多元线性回归，认为xt主 要受过去p期的序列值影响。误差项是当前的随机干扰εt，为零均值白噪声序列。

（2）MA模型

具有如下结构的模型称为q阶自回归模型，简记为MA(q)：

即在t时刻的随机变量Xt的取值Xt是前q期的随机扰动εt-1,εt−2,...,εt−qεt−1,εt−2,...,εt−q的多元线性函数。误差项是当期的随机干扰εt,为零均值白噪声序列，μ是序列{Xt}的均值。认为xt主要受过去q期的误差项影响。

（3）ARMA模型

ARMA模型是最常用的平稳序列拟合模型，随机变量Xt的取值xt不仅与以前p期的序列值有 关还与前q期的随机扰动有关。

这三种模型适用的情景也不同，具体的可以查阅一下。总的来说，基于此类方法的建模步骤是，首先需要对观测值序列进行平稳性检测，如果不平稳，则对其进行差分运算直到差分后的数据平稳；在数据平稳后则对其进行白噪声检验，白噪声是指零均值常方差的随机平稳序列；如果是平稳非白噪声序列就计算ACF（自相关系数）、PACF（偏自相关系数），进行ARMA等模型识别，对已识别好的模型，确定模型参数，最后应用预测并进行误差分析。

这类方法本人也几乎没用过，一般是统计或者金融出身的人用的比较多，如果要深入研究这块的话，对统计学或者随机过程知识的要求还是很高的。而在数据挖掘的场景中还是很少用的，比如有一个连锁门店的销售数据，要预测每个门店的未来销量，用这类方法的话就需要对每个门店都建立模型， 这样就很难操作了。

2.现代预测方法

这就指的是机器学习方法以及深度学习方法。

对于机器学习方法，xgboost，随机森林及SVM这些都是可以用的，也没有说哪个模型好用，需要看具体的场景及实验，总之就是看效果说话。那么，用数据挖掘的方法关键在于特征工程，跟其他挖掘任务不同的是，时间序列的特征工程会使用滑动窗口，即计算滑动窗口内的数据指标，如最小值，最大值，均值，方差等来作为新的特征。

对于深度学习方法，循环神经网络RNN用的最多也适合解决这类问题，但是，卷积神经网络CNN，及新出的空间卷积网络TCN都是可以尝试的。

3.一些需要注意的

实际场景中我们需要处理的时间序列往往会是没有趋势，非平稳的，但并不是说非平稳就一点都预测不了了。

(1) 概念漂移

所谓概念漂移，表示目标变量的统计特性随着时间的推移以不可预见的方式变化的现象，也就是每过一段时间序列的规律是会变化的。所以，在这种情况下，拿全部时间内的数据去训练，就相当于是增加了各种噪声，预测精度是会下降的。所以，一种解决办法是不断的取最新的一阶段内的数据来训练模型做预测。之前做过一个变压器油温预测的数据，实验了用全量数据，一年内的数据，半年，3个月，一个月的数据做训练，其后几天的数据做预测，发现一个月的效果是最好的。那么如果你要问我，怎么判断一个序列是否存在概念漂移，我会告诉你，我也不知道，做实验吧！（有相关论文可以查阅一下）

（2）序列的自相关性

做过时间序列的朋友可能常常会有这样的感受，用了某种算法做出来的测试集的平均绝对误差率或者r2系数都很好，但是把测试集的真实值及预测值画出来对比一下，就会发现t时刻的预测值往往是t-1时刻的真实值，也就是模型倾向于把上一时刻的真实值作为下一时刻的预测值，导致两条曲线存在滞后性，也就是真实值曲线滞后于预测值曲线，就像下图右边所显示的那样。之所以会这样，是因为序列存在自相关性，如一阶自相关指的是当前时刻的值与其自身前一时刻值之间的相关性。因此，如果一个序列存在一阶自相关，模型学到的就是一阶相关性。而消除自相关性的办法就是进行差分运算，也就是我们可以将当前时刻与前一时刻的差值作为我们的回归目标。但是，在其他任务进行特征选择的时候，我们是会把目标变量相关性低的特征去掉，留下相关性强的特征。

还有一点需要注意的是，单纯使用平均绝对误差率或者r2系数容易误导，因为即使指标效果很好，但是很有可能这个模型也是没有用的。一种做法是可以计算一个基准值，即如果全部预测值都采用上一时刻的真实值，这时候的平均绝对误差率或者r2系数是多少，如果你以后加了其他特征，依然没办法超过这个基准值或者提升不大，那就放弃吧，这个时间序列可能已经没办法预测了。

（3）训练集和测试集的划分

在时间序列任务上，如果还跟其他任务一样随机划分训练集和测试集那就是甩流氓。随机划分的测试集，跟训练集的分布会是很接近的，效果肯定比一刀切的方法更好。因此，一般是选取某个时间节点之前作为训练集，节点之后作为测试集。比如有2012-2015年预测很多家店的未来的销量，那训练集可以是每家店2012-2014的数据，测试集是每家店2015年的数据。

（4）时间序列分解

这段内容参考自这里。对于无明显周期和非平稳时序数据，直接预测难以达到满意效果，可以利用经验模式分解(empirical mode decomposition,EMD)和长短期记忆(long short-term memory, LSTM)的组合算法应用于时序预测。将时序数据通过EMD算法进行分解,然后将分解后的分量数据分别转化为三维数据样本。对归一化的分量数据和原始数据分别进行预测建模及其 重构。实验结果表明EMD-LSTM更能有效的表达出家庭短期负荷的时序关系，具有更高的预测精度。所谓经验模式分解，能使复杂信号分解为有限个本征模函数（Intrinsic Mode Function，简称IMF），所分解出来的各IMF分量包含了原信号的不同时间尺度的局部特征信号，可以达到降噪的目的。另外看到类似的做法还有小波变换，这一块比较涉及数字信号的知识了。

欢迎各位指出错误或提出建议！orz。