AcWing 1081. 度的数量（数位DP）

一、问题

二 、数位DP

这道题是一道数位DP的题目，其实数位DP更像我们在高中阶段学过的排列组合问题中的分类讨论。

数位DP顾名思义就是按照数字的每一位去讨论。

那么数位DP做题思路分为两步：按位枚举，分类讨论

我们把区间的上限X写出来：

那么怎么分类讨论呢？

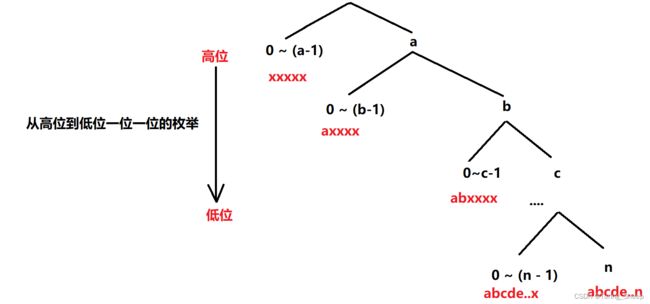
从上到下是从高位到低位枚举的，对于每一位我们的分类依据是：(0 ~ a - 1)和a，那么为什么这么分呢？

一般数位DP都是让我们挑选满足某个条件的数，我们不仅需要考虑某个数是否满足条件，还需要考虑某个数是否小于上限值。

那么我们在分类讨论以后，就发现我们分出的第一类情况中：0~a-1，由于高位都小于了a，那么这个数肯定比上限X小，也就是说此时我们只需要考虑是否满足题目中的某个条件。

我们对每一位都做这样的操作，只不过越往下分，每个数字固定的前缀就越长，最后我们会发现所有二叉树的右儿子恰好组成了我们上限值。

那么有人可能会想，题目中问的有可能是个区间，难道我们不需要考虑这个数必须大于等于下限吗？

这里可以使用一个思路，假设$f[n]$是满足所有小于等于上限值的数的数量，我们只需要再减去小于下限m的数目，即$f[m-1]$的值，就是区间$[n,m]$内符合题目条件的数目。

三、解析

1、题意理解

这道题根据题意可以将问题转化为，如果区间内的某个数转为B进制的表示方式的时候，表示方式中只有$k$个1的条件下，这个数就是合法的，然后我们需要统计所有合法的数字数目。

2、题目分析

按照刚刚题意理解，我们发现符合题意的数字按照B进制展开以后，应该只是由0和1组成的。并且1的个数是k个。

我们拿出某一位进行讨论：

假设这一位是a，该位后面还有n位上的数不确定。

如果该位写的是0 ~ a-1，那么我们就不需要考虑大小，只考虑条件。

那么在不考虑数字大小，仅考虑题目要求的情况下，我们该怎么算呢？

需要注意的是，虽然我们可以在0~a-1之间选数，但是题目要求只能写0或者1。

设：

当前位的后面还有$n$位，并且当前位前面已经写了$last$个$1$，而我们总共需要写$k$个$1$。

如果当前位也写了$1$，那么现在这个数中已经有了$last+1$个$1$，我们只需要在后面的$n$位中拿出$(k-last-1)$个$1$，根据组合数，

这种情况一种有：$C_n^{k-last-1}$种情况。

如果当前位没有写$1$，写的是$0$，则说明我们还需要写$k-last$个数，此时的情况数为$C_{n}_{k-last}。

我们只需要将两个组合数加在一起就是该分类下的情况。

那么对于另一种情况：该位写a。

我们就需要继续分类讨论，但如果a是1的话，我们需要更新一下1的个数。

由于这道题只要0或者1，所以使得题目有了一定的简化。

如果该位最大是a的话，并且a是大于1的，那么我们写0还是1都不会超过上限，所以此时就可以直接不用继续讨论了，直接得出结果就行了。

知道这个规律后，我们可以适当更改一下我们分类讨论的依据，如果该位的最大值a>1，那么我们直接求出两个组合数加在一起，终止讨论。

如果a = 1的话，我们就按照数位DP的方式讨论，分为左支和右支。

如果a = 0的话，这一位只能写0。

分类到最后，我们需要判断一下由刚才描绘的那棵树的右支组成的数，即上限值，是否满足条件，如果满足的话，我们需要对结果+1。

由于涉及到了组合数，所以我们需要预处理出来会用到的组合数。

不会的同学去看作者写的这篇文章：第三十二章 数论——组合数详解（1）

三、代码

 	#include
using namespace std;
const int N = 40;
int C[N][N];
int x, y, k, b;
void init()
{
	for(int i = 0; i <= N; i ++ )
	{
		for(int j = 0; j <= i; j ++ )
		{
			if(!j)C[i][j] = 1;
			else C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
		}
	}
}
int dp(int n)
{
	int res = 0;
	vector<int>v;
	int last = 0;
	while(n)
	{
		v.push_back(n % b);
		n /= b;
	}
	for(int i = v.size() - 1; i >= 0; i -- )
	{
		int a = v[i];
		if(a)
		{
			if(a > 1)//a>1的时候，直接答案返回
			{
				if(k - last - 1 >= 0)
					res += C[i][k - last - 1];
				if(k - last >= 0)
					res += C[i][k - last];
				break;
			}
			else//a = 1的时候
			{
				if(k - last >= 0)
					res += C[i][k - last];//分类讨论中的左支：这一位写0，后面随别写
				last ++;//分类讨论的右边：这一位写了1，所以1的数目++
			}
		}
		if(!i && last == k)res++;
	}
	return res;
}
int main()
{
	init();
	cin >> x >> y >> k >> b;
	cout << dp(y) - dp(x - 1) << endl;
	return 0;
}