(学习笔记)图像处理——Retinex增强
文章目录
-
- 前言
- 原理
- 发展
-
- 单尺度算法(SSR)
- 多尺度算法(MSR)
- 带有色彩恢复的多尺度
- 实现
前言
Retinex算法由Land于1986年在《An alternative technique for the computation of the designator in the retinex theory of color vision》一文中提出,其实质上是一种基于光照补偿的图像增强算法。图像处理领域主要应用在:
- 光照不均匀图像的抑制
- 图像亮度增强,细节的保护,色彩的保护,自然度的恢复等等
- 图像去噪(噪声属于高频信息,可将噪声留在反射分量中再去噪)
- 细节提取(类似于Canny边缘提取)
- 图像结构和纹理的单部分获取
原理
输入图像由照度分量和反射分量两部分组成,即:
I ( x , y ) = L ( x , y ) R ( x , y ) I(x,y)=L(x,y)R(x,y) I(x,y)=L(x,y)R(x,y)
其中, L L L为亮度分量,描述照明,变化缓慢,处于低频部分; R R R为反射分量,描述景物细节,变化较快,处于高频部分。
Retinex算法对图像的处理目的就是从图像 I I I中获取反射分量 R R R。算法流程如下:

发展
Retinex算法理论有两个经典算法:基于路径的Retinex以及基于中心环绕Retinex。基于中心环绕Retinex又从单尺度(Single Scale Retinex)到多尺度(Multi Scale Retinex),再发展至带有色彩恢复的多尺度(Multi Scale Retinex with Color Restoration)以及其他更多的改进。在此只学习基于中心环绕的三个典型算法。
单尺度算法(SSR)
步骤:
第一步:输入原图像 I ( x , y ) I(x,y) I(x,y),分离三个颜色分量;
第二步:构建高斯环绕函数 G ( x , y ) = K e − x 2 + y 2 σ 2 G(x,y)=K e^{-\frac{x^{2}+y^{2}}{\sigma^{2}}} G(x,y)=Ke−σ2x2+y2,确定尺度参数 σ \sigma σ,一般取80至100,K为归一化常数,满足 ∫ ∫ G ( x , y , σ ) d x d y = 1 \int\int G(x,y,\sigma)dxdy=1 ∫∫G(x,y,σ)dxdy=1;
第三步:利用高斯环绕分别对B、G、R三个通道进行滤波 L ( x , y ) = I ( x , y ) ∗ G ( x , y ) L(x,y)=I(x,y)\ast G(x,y) L(x,y)=I(x,y)∗G(x,y),滤波后的图像便是所估计的光照分量 L ( x , y ) L(x,y) L(x,y);
第四步:取对数并对原始图像和光照分量进行相减 log R ( x , y ) = log I ( x , y ) L ( x , y ) = log I ( x , y ) − log L ( x , y ) \log R(x,y)=\log \frac{I(x,y)}{L(x,y)}=\log I(x,y)-\log L(x,y) logR(x,y)=logL(x,y)I(x,y)=logI(x,y)−logL(x,y);
第五步:做指数变换 e log R ( x , y ) = R ( x , y ) e^{\log R(x,y)}=R(x,y) elogR(x,y)=R(x,y),但实际操作中一般先计算出 log R ( x , y ) \log R(x,y) logR(x,y)的最大值Max和最小值Min,然后对每个值Value进行线性量化: R ( x , y ) = ( V a l u e − M i n ) ( 255 − 0 ) ( M a x − M i n ) R(x,y)=\frac{(Value-Min)(255-0)}{(Max-Min)} R(x,y)=(Max−Min)(Value−Min)(255−0);
第六步:输出反射分量作为结果图像。

注: 高斯函数 σ \sigma σ是唯一可调的参数,和高斯滤波一样,对结果有直接影响。
多尺度算法(MSR)
SSR算法在动态范围压缩和色调恢复的两种效果中不能兼得,只能牺牲一种来得到另一种,因此基于该缺点提出了不同尺度下的增强结果线性地组合在一起,将局部信息和整体信息考虑进去的多尺度算法,最终能得到具有良好动态范围压缩、色彩稳定性和色彩恢复的图片。
其基本思想是:将图像依照灰度值分为若干级,分别使用单尺度风阀,最后使用系数加权得到处理结果。
步骤:
第一步:输入原图像 I ( x , y ) I(x,y) I(x,y),按灰度值分为若干尺度级,并分离三个颜色分量;
第二步:构建尺度参数不同的高斯环绕函数: G k ( x , y ) G_{k}(x,y) Gk(x,y),一般建立三个尺度比例为 15 : 80 : 250 15:80:250 15:80:250较为合适;
第三步:利用高斯环绕函数分别对B、G、R三个通道进行卷积滤波,并加权平均得到照度分量 L ( x , y ) = ∑ k = 1 N ω k ( I i ( x , y ) ∗ G k ( x , y ) ) L(x,y)=\sum_{k=1}^{N}\omega_{k}(I_{i}(x,y)\ast G_{k}(x,y)) L(x,y)=∑k=1Nωk(Ii(x,y)∗Gk(x,y)),其中, ∑ k = 1 N ω k = 1 \sum_{k=1}^{N}{\omega_{k}}=1 ∑k=1Nωk=1;
第四步:取对数并对原始图像和光照分量进行相减 log R i ( x , y ) = ∑ k = 1 N ω k ( log ( I i ( x , y ) ) − log ( I i ( x , y ) ∗ G k ( x , y ) ) ) \log R_{i}(x,y)=\sum_{k=1}^{N}\omega_{k}(\log(I_{i}(x,y))-\log(I_{i}(x,y)\ast G_{k}(x,y))) logRi(x,y)=∑k=1Nωk(log(Ii(x,y))−log(Ii(x,y)∗Gk(x,y)));
第五步:将对数域转变到实数域 R ( x , y ) R(x,y) R(x,y);
第六步:输出反射分量作为结果图像。
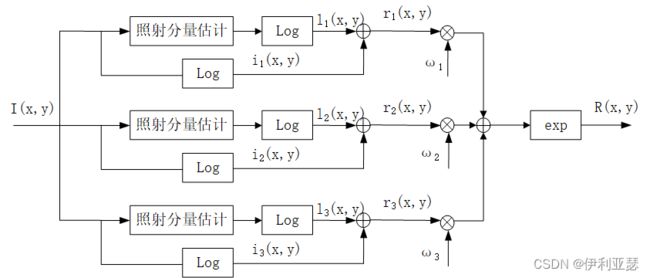
可以发现相对于单尺度,多尺度算法对第二和第三两个步骤进行了改进。
带有色彩恢复的多尺度
MSRCR
在前两种方法中图像可能会有局部细节色彩失真,不能显出物体的真正颜色,所以针对这点Daniel J. Jobson等人于1997年在《A Multiscale Retinex for Bridging the Gap Between Color Images and the Human Observation of Scenes》一文提出了MSRCR该算法在MSR的基础上增加了一个色彩恢复的步骤。

色彩恢复 c i ( x , y ) = I i ( x , y ) ∑ j = 1 N I j ( x , y ) c_{i}(x,y)=\frac{I_{i}(x,y)}{\sum_{j=1}^{N}I_{j}(x,y)} ci(x,y)=∑j=1NIj(x,y)Ii(x,y),其中, I i ( x , y ) I_{i}(x,y) Ii(x,y)是原图像像素值,在RGB色彩空间中N=3, i , j i,j i,j表示三个色彩通道。
对其做对数变换可得:
C i ( x , y ) = β ⋅ log [ α ⋅ c i ( x , y ) ] = β ⋅ { log [ α ⋅ I i ( x , y ) ] − log [ ∑ j = 1 N I j ( x , y ) ] } C_{i}(x,y)=\beta \cdot \log[\alpha \cdot c_{i}(x,y)]=\beta \cdot\{\log[\alpha \cdot I_{i}(x,y)]-\log[\sum_{j=1}^{N}I_{j}(x,y)]\} Ci(x,y)=β⋅log[α⋅ci(x,y)]=β⋅{log[α⋅Ii(x,y)]−log[j=1∑NIj(x,y)]}
其中, α \alpha α 用来调节非线性变换, β \beta β是增益常数。
MSRCR计算公式为:
log R M S R C R i ( x , y ) = C i ( x , y ) ⋅ log R M S R i ( x , y ) = β ⋅ log R M S R i ( x , y ) { log [ α ⋅ I i ( x , y ) ] − log [ ∑ j = 1 N I j ( x , y ) ] } \log R_{MSRCR_{i}}(x,y)=C_{i}(x,y)\cdot \log R_{MSR_{i}}(x,y)=\beta \cdot \log R_{MSR_{i}}(x,y)\{\log[\alpha \cdot I_{i}(x,y)]-\log[\sum_{j=1}^{N}I_{j}(x,y)]\} logRMSRCRi(x,y)=Ci(x,y)⋅logRMSRi(x,y)=β⋅logRMSRi(x,y){log[α⋅Ii(x,y)]−log[j=1∑NIj(x,y)]}
实际中需要对对数域中的像素值进行拉伸处理,可得到MSRCR计算公式为:
log R M S R C R i ( x , y ) = G [ C i ( x , y ) ⋅ log R M S R i ( x , y ) + b ] = G [ C i ( x , y ) { log I i ( x , y ) − log [ I i ( x , y ) ∗ G n ( x , y ) ] } + b ] \log R_{MSRCR_{i}}(x,y)=G[C_{i}(x,y)\cdot \log R_{MSR_{i}}(x,y)+b]=G[C_{i}(x,y)\{\log I_{i}(x,y)-\log[I_{i}(x,y)\ast G_{n}(x,y)]\}+b] logRMSRCRi(x,y)=G[Ci(x,y)⋅logRMSRi(x,y)+b]=G[Ci(x,y){logIi(x,y)−log[Ii(x,y)∗Gn(x,y)]}+b]
其中,G和b为经验参数。
具有颜色恢复的多尺度 Retinex (MSRCR) 将小尺度 Retinex 的动态范围压缩和大规模 Retinex 的色调再现与普遍应用的颜色恢复相结合。
实现
SSR:
# SSR
import cv2
from numpy import nonzero
from numpy import float32
from skimage.metrics import peak_signal_noise_ratio
from skimage.metrics import structural_similarity
import csv
def replaceZeroes(data):
min_nonzero = min(data[nonzero(data)])##data中不为0数字的位置中的最小值
data[data == 0] = min_nonzero##data中为0的位置换为最小值
return data
def SSR(img, sigma):
B, G, R = cv2.split(img)
def channel(C):
L_C = cv2.GaussianBlur(C, (5, 5), sigma)##L(x,y)=I(x,y)∗G(x,y)
h, w = C.shape[:2]
C = replaceZeroes(C)
C = C.astype(float32) / 255
L_C = replaceZeroes(L_C)
L_C = L_C.astype(float32) / 255
dst_C = cv2.log(C) ##logI(x,y)
dst_L_C = cv2.log(L_C) ##logL(x,y)
log_R_C = cv2.subtract(dst_C, dst_L_C) ##logR(x,y)=logI(x,y)−logL(x,y)
minvalue, maxvalue, minloc, maxloc = cv2.minMaxLoc(log_R_C) ##量化处理
for i in range(h):
for j in range(w):
log_R_C[i, j] = (log_R_C[i, j] - minvalue) * 255.0 / (maxvalue - minvalue) ##R(x,y)=(value-min)(255-0)/(max-min)
C_uint8 = cv2.convertScaleAbs(log_R_C)
return C_uint8
B_uint8 = channel(B)
G_uint8 = channel(G)
R_uint8 = channel(R)
image = cv2.merge((B_uint8, G_uint8, R_uint8))
return image
##存储数据
def writeCsv(image, psnr, ssin):
row = [image, psnr, ssim]
out = open("D:/Retinex/SSR/result.csv", "a", newline="")
csv_writer = csv.writer(out, dialect="excel")
csv_writer.writerow(row)
##输入图片执行
for j in range(10, 100):
test = cv2.imread("D:/Infrared_image/00{}.jpg".format(str(j)))
print(f"00{j}.jpg:")
result = SSR(test, 80)
#cv2.imshow("test", test)
#cv2.imshow("result", result)
cv2.imwrite("D:/Retinex/SSR/result/00{}.jpg".format(str(j)), result)
key = cv2.waitKey(0)
cv2.destroyAllWindows()
#writeCsv("image", "psnr", "ssim") ##表头
# 计算psnr及ssim
test = cv2.cvtColor(test, cv2.COLOR_BGR2GRAY) # 转换为灰度图片
result = cv2.cvtColor(result, cv2.COLOR_BGR2GRAY)
psnr = peak_signal_noise_ratio(test, result)
ssim = structural_similarity(test, result)
# print(f"psnr={psnr}")
# print(f"ssim={ssim}")
writeCsv(j, psnr, ssim)
对应psnr为:13.1918870131122
对应ssim为:0.673577787550732
MSR:
# MSR
def MSR(img, sigma_list):
B, G, R = cv2.split(img)
weight = 1 / 3.0
scales_size = 3
def channel(C, sigma_list):
for i in range(0, scales_size):
C = replaceZeroes(C)
C = C.astype(float32) / 255
L_C = cv2.GaussianBlur(C, (5, 5), sigma_list[i])##L(x,y)=I(x,y)∗G(x,y)
print(sigma_list[i])
h, w = C.shape[:2]
log_R_C = zeros((h, w), dtype=float32)
L_C = replaceZeroes(L_C)
L_C = L_C.astype(float32) / 255
log_C = cv2.log(C)##logI(x,y)
log_L_C = cv2.log(L_C)##logL(x,y)
log_R_C += weight * cv2.subtract(log_C, log_L_C)##=logR(x,y)=w(logI(x,y)−logL(x,y))
minvalue, maxvalue, minloc, maxloc = cv2.minMaxLoc(log_R_C)
for i in range(h):
for j in range(w):
log_R_C[i, j] = (log_R_C[i, j] - minvalue) * 255.0 / (maxvalue - minvalue) ##R(x,y)=(value-min)(255-0)/(max-min)
C_uint8 = cv2.convertScaleAbs(log_R_C)
return C_uint8
B_uint8 = channel(B, sigma_list)
G_uint8 = channel(G, sigma_list)
R_uint8 = channel(R, sigma_list)
image = cv2.merge((B_uint8, G_uint8, R_uint8))
return image
输入图片与SSR一样,
sigma_list为15,80,250时输出为:

对应psnr为:13.2062748786571
对应ssim为:0.67356703973411
MSRCR:
def replaceZeroes(data):
min_nonzero = min(data[nonzero(data)])
data[data == 0] = min_nonzero
return data
def colorRestoration(img, alpha, beta):
img_sum = np.sum(img, axis=None, keepdims=True)
color_restoration = beta * (np.log10(alpha * img) - np.log10(img_sum))#求取C
return color_restoration
def simplestColorBalance(img, low_clip, high_clip):
total = img.shape[0] * img.shape[1]
for i in range(img.shape[2]):
unique, counts = np.unique(img[:, :, i], return_counts=True)
current = 0
for u, c in zip(unique, counts):
if float(current) / total < low_clip:
low_val = u
if float(current) / total < high_clip:
high_val = u
current += c
img[:, :, i] = np.maximum(np.minimum(img[:, :, i], high_val), low_val)
return img
def MSR(img, sigma_list):
B, G, R = cv2.split(img)
weight = 1 / 3.0
scales_size = 3
def channel(C, sigma_list):
for i in range(0, scales_size):
C = replaceZeroes(C)
C = C.astype(float32) / 255
L_C = cv2.GaussianBlur(C, (5, 5), sigma_list[i])##L(x,y)=I(x,y)∗G(x,y)
#print(sigma_list[i])
h, w = C.shape[:2]
log_R_C = zeros((h, w), dtype=float32)
L_C = replaceZeroes(L_C)
L_C = L_C.astype(float32) / 255
log_C = cv2.log(C)##logI(x,y)
log_L_C = cv2.log(L_C)##logL(x,y)
log_R_C += weight * cv2.subtract(log_C, log_L_C)##=logR(x,y)=w(logI(x,y)−logL(x,y))
minvalue, maxvalue, minloc, maxloc = cv2.minMaxLoc(log_R_C)
for i in range(h):
for j in range(w):
log_R_C[i, j] = (log_R_C[i, j] - minvalue) * 255.0 / (maxvalue - minvalue) ##R(x,y)=(value-min)(255-0)/(max-min)
C_uint8 = cv2.convertScaleAbs(log_R_C)
return C_uint8
B_uint8 = channel(B, sigma_list)
G_uint8 = channel(G, sigma_list)
R_uint8 = channel(R, sigma_list)
image = cv2.merge((B_uint8, G_uint8, R_uint8))
return image
def MSRCR(img, sigma_list, G, b, alpha, beta, low_clip, high_clip):
img = np.float64(img) + 1.0
img_retinex = MSR(img, sigma_list)#先做MSR处理
img_color = colorRestoration(img, alpha, beta)#计算色彩恢复C
img_msrcr = G * (img_retinex * img_color + b)#MSRCR处理
for i in range(img_msrcr.shape[2]):
img_msrcr[:, :, i] = (img_msrcr[:, :, i] - np.min(img_msrcr[:, :, i])) / \
(np.max(img_msrcr[:, :, i]) - np.min(img_msrcr[:, :, i])) * \
255 #转换为实数域
img_msrcr = np.uint8(np.minimum(np.maximum(img_msrcr, 0), 255))#图片格式恢复
img_msrcr = simplestColorBalance(img_msrcr, low_clip, high_clip)#色彩平衡处理
return img_msrcr
输入图片同上
输出结果为:

对应psnr为:5.7753713026592
对应ssim为:0.0997847741077085
个人学习笔记分享,错误望请指正!

