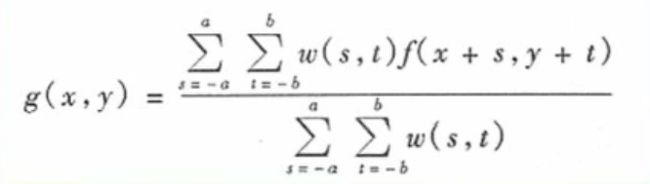数字图像处理——第三章 灰度变换与空间滤波

3.1 灰度变换

灰度变换是在空间域上执行的，灰度变换对图像的单个像素进行操作，主要以对比度和与之处理为目的。空间域处理可由公式g(x,y)=T[f(x,y)]表示，式中，f(x,y)是输入图像，g(x,y)是处理过的图像，T为定义的关于f的一种算子。
在处理过程中，要引入邻域的概念，首先算法定位于处理的（x，y）像素的位置，再处理中心点m个邻域的灰度，最后通过计算得出灰度值。
灰度变换变换公式可以使过亮的、过暗的地方都提升对比度，极端情况下，会产生二值（阈值）图像。

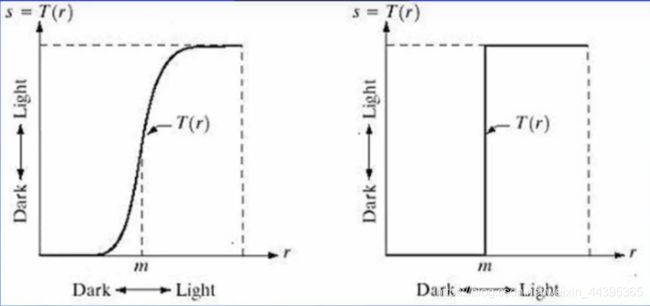
from skimage import data,filters
thresh = filters.threshold_otsu(img)   #返回一个阈值
img004 =(img <= thresh)*1.0   #根据阈值进行分割

plt.figure('thresh',figsize=(8,8))

plt.subplot(121)
plt.title('original image')
plt.imshow(img,plt.cm.gray)

plt.subplot(122)
plt.title('binary image')
plt.imshow(img004,plt.cm.gray)

plt.show()

阈值函数处理后变成黑白图像

3.2 基本灰度变换函数

图像反转 公式：s=L-1-r 适用于嵌入图像暗色区域的白色或灰色细节
对数变换 公式：s=clog(1+r) 用于扩展像素中的像素值，同时压缩更高灰度级的值，结果输出的像素范围要相同,256灰度情况下，s=$\frac{clog(1+r)-clog(1+0)}{clog(1+255)-clog(1+0)}\times 255$,r,s属于[0,255]。
幂次变换 公式：s=cr${}^k$,k互为相反数时结果相反。
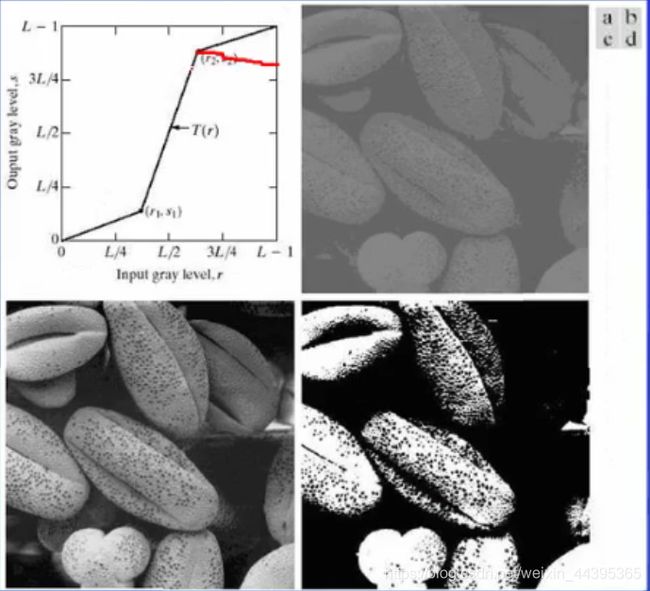
分段线性变换函数，能够使变换结果更加适应实际情况。包括对比拉伸，灰度切割与位图切割。

对比拉伸是设置几个不同的线性关系，使图像更为自然，见第一张下图；
灰度切割是突出关心的区域，使关心区域范围灰度值高，其余范围灰度值不变或是为0；
位图切割是得到某m比特图像的m个比特平面，也是m个灰度图，在图像处理有时是有用的，见第二张下图的应用。

## 图像定义与读取
import matplotlib.pyplot as plt
import cv2 as cv
import numpy as np

def show(img):
    if img.ndim==2:
       plt.imshow(img,cmap='gray')
    else:
       img=cv.cvtColor(img,cv.COLOR_BGR2RGB)
       plt.imshow(img)
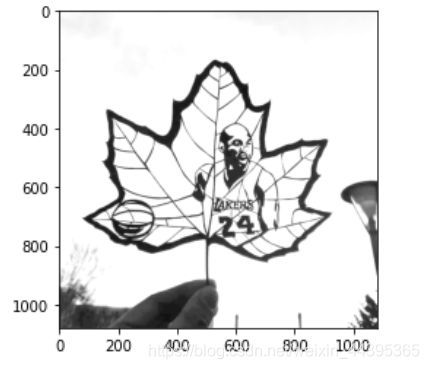
img=cv.imread('pic/kobe_mamba.jpg.',0)   ##打开灰度图 只有[0,255]
show(img)

## 图像反转
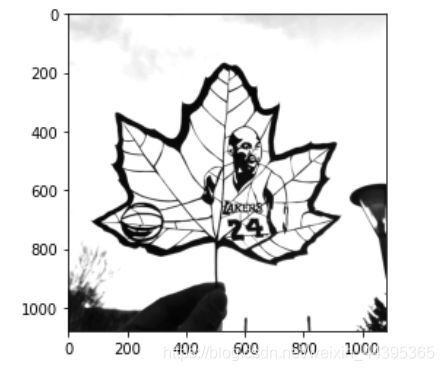
img001=255-img
show(img001)
## 线性变换
b=20
k=2
img2=b+k*img.astype(np.int32)  ##转换为无符号32位
show(img2)
img2=np.clip(img2,0,255)   ## 设置灰度范围
show(img2)
## 非线性变换
img2=np.clip(img2,0,255)
img3=10+np.log(img2+1)/0.5   ##非线性变换
show(img3)
## 幂次变换
img6=img2/255  ##gamma变换
img4=np.power(img6,0.5)*255   ##次方函数
img5=np.power(img6,2)*255
img7=np.hstack([img4,img5])
show(img7)

结果图：
原图与反转：

对数变换：

幂次变换：

线性变换：

3.3 直方图处理

3.3.1 直方图均衡

灰度级范围为[0,L-1]的数字图像的直方图是离散函数h（r${}_k$）=n${}_k$，其中rk是第k级灰度值，n${}_k$是图像中灰度为r${}_k$的像素个数。在实践中，经常用乘积MN表示的图像像素的总数除它的每个分量来归一化直方图，通常M和N是图像的行和列的维数。因此，归一化后的直方图由p（r${}_k$）=n${}_k$/MN给出，其中k=0,1,…,L-1。简单来说，p（r${}_k$）是灰度级r${}_k$在图像中出现的概率的一个估计。归一化直方图的所有分量之和应等于1。

我们注意到，暗图像的分量集中于低端，亮图像相反，低对比度图像集中于灰度图的中部，若直方图均衡化，能得到一幅灰度级丰富且动态范围大的图像，关键是寻找变换函数。
S${}_k$=T($r_k$)=${\sum }_{j=0}^k$P${}_r$(r${}_j$)


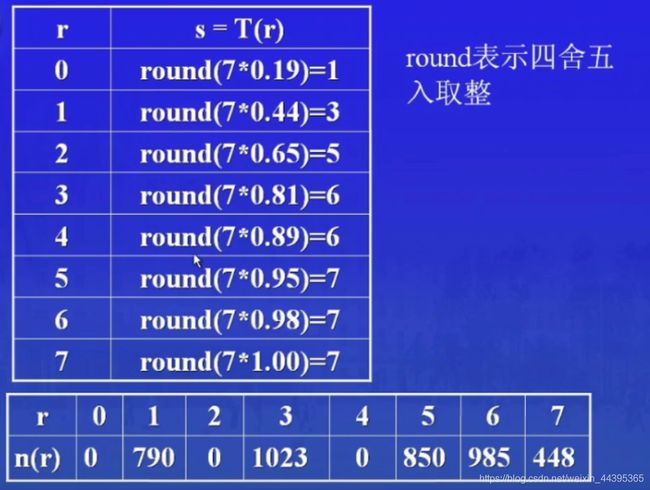
得出灰度变换函数。

均衡化步骤：

统计图像中每个灰度级出现的次数，计算图像中每个灰度级出现的概率；
根据变换公式得到直方图均衡化的变换函数；
根据变换函数映射到每个像素点；
输出映射后的图像；

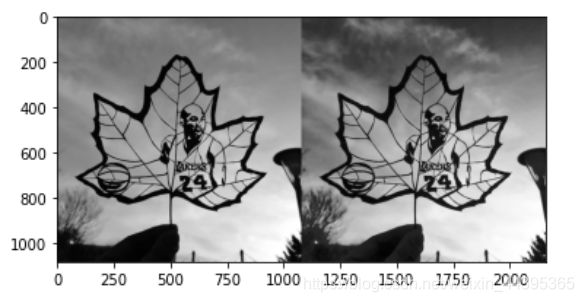
img01=cv.equalizeHist(img)    ##直方图均衡函数
show(np.hstack([img,img01]))   

均衡化的图像对比度增强

##统计原图像直方图
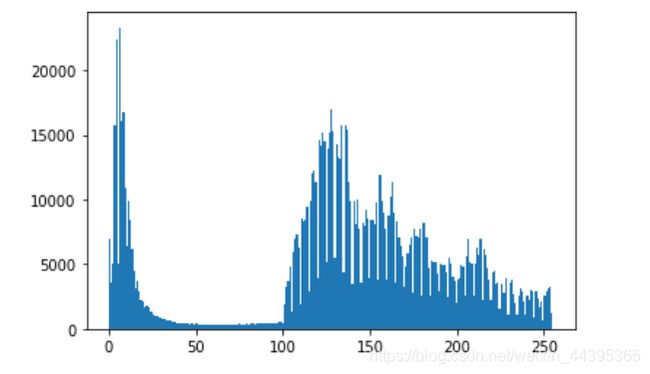
hist=cv.calcHist([img],[0],None,[256],[0,256])   ##通道0（灰度图像） 统计整幅图的灰度值分布
plt.hist(img.ravel(),256)
plt.show()

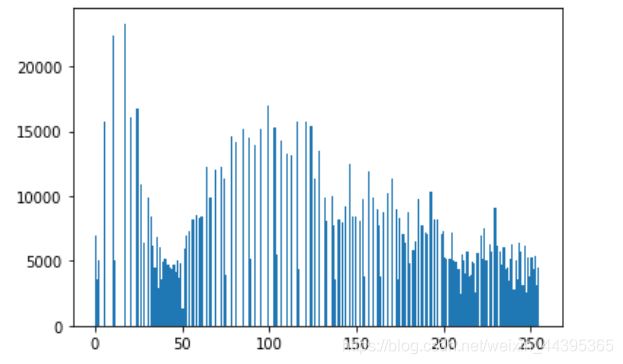
##均衡化后的直方图
hist=cv.calcHist([img01],[0],None,[256],[0,256])   ##通道0（灰度图像） 统计整幅图的灰度值分布
plt.hist(img01.ravel(),256)    ##将图像转换成一维数组
plt.show()

3.3.2 直方图匹配

r和z分别表示输入图像和输出图像（已处理）的灰度级。S=T（r）=${\int }_0^r$p${}_r$(w)dw=${\int }_0^z$p${}_z$(t)dt=G(z),z是G（s）的反函数，V${}_j$=G(z),对S${}_j$寻找最近的V${}_k$，对应的z${}_k$是r${}_j$映射的灰度值。

直方图匹配的映射举例：

## 自适应的均衡化
clahe=cv.createCLAHE(clipLimit=50,tileGridSize=(8,8))
clahe1=clahe.apply(img)
show(np.hstack([img,img01,clahe1]))

原图像+均衡化图像+自适应均衡化图像

3.3.3 应用直方图进行局部增强

平均灰度m=${\sum }_{i=0}^{L-1}$r${}_i$p(r${}_i$),二阶矩${\sum }_{i=0}^{L-1}$（r${}_i$-m）${}^2$=$\sigma (r{)}^2$,即方差。判断暗、亮是将局部平均灰度与全局平均灰度相比较，判断对比度是判断局部标准差和全局标准差。局部增强的方法是在图像的像素领域中，根据灰度级分布设置变换函数。

3.4 空间滤波基础

空间滤波器也被称为空间掩膜，核，模板和窗口。空间滤波器由一个领域（通常是一个矩形），对该领域的图像像素执行预定义操作，预定义操作是处理领域有相同维数的子图像的值，为系数值，不是像素值。
g(x,y)=${\sum }_{s=-a}^a$${\sum }_{t=-b}^b$w(s,t)*f(x+s,y+t)，其中g(x,y)代表的是滤波器响应，w(s,t)代表的是系数值，f(x${}_0$,y${}_0$)所对应的是像素值。由于该公式与频率域中卷积处理概念相似，也称为“掩模与图像的卷积”。
离散卷积公式x${}_1$(n)*x${}_2$(n)=$\sum$x${}_1$(k)x${}_2$(n-k)，通过比较可知，第一个公式是相关公式，卷积要先反转方向，相关和卷积得到的结果是相差180${}^o$的。

3.5 平滑空间滤波器

平滑滤波器用于模糊处理和降低噪声，模糊处理常用于预处理任务中，通过线性滤波和非线性滤波，降低噪声。

3.5.1 平滑线性滤波器

平滑线性滤波器的输出是包含在滤波器模板领域内的像素的简单平均值，使用平均灰度值来代替图像中每个像素的值，但其存在着边缘模糊的效应，有两种平均方法，一种是直接平均，另一种是加权平均。

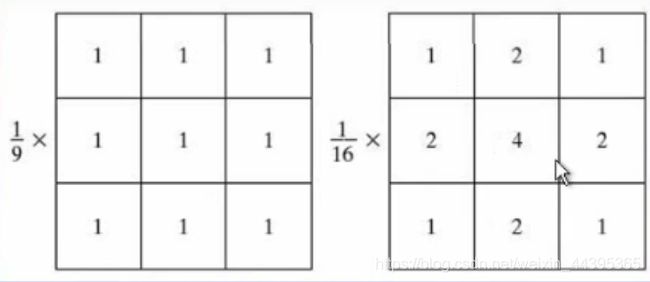
计算过程：

加权公式如下：

均值模糊：cv.blur(img,(x*x))
卷积：cv.filter2D(img,-1,kernel)

左图为噪声图，右图为均值模糊结果图

##卷积
A=np.ones((3,3))
print(A)
B=np.ones((4,4))
print(B)
C=cv.filter2D(A,-1,B)
print(C)

3.5.2 非线性滤波器

分类 ：
中值滤波器： 用像素领域内的中间值代替该像素
主要用途：去除噪声（尤其是椒盐噪声[即以黑白点的形式叠加在图像上的]）
计算公式：R = mid { | k = 1,2,…,n}
最大值滤波器：用像素领域内的最大值代替该像素
主要用途：寻找最亮点
计算公式：R = max { | k = 1,2,…,n}
最小值滤波器：用像素领域内的最小值代替该像素
主要用途：寻找最暗点
计算公式：R = min { | k = 1,2,…,n}

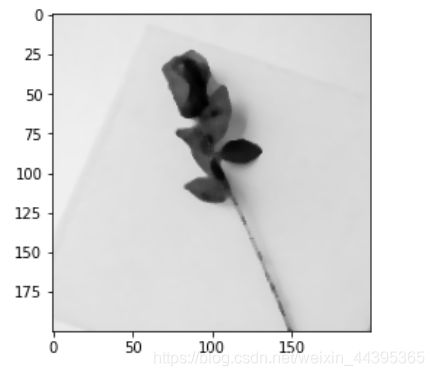
##中值滤波
rose_media=cv.medianBlur(rose_noise,5)
show(rose_media)

与上图噪音图和均衡平均作比较，可发现去除了噪音点。

3.6 锐化空间滤波器

图像模糊可通过空间域用像素领域平均法实现，我们可以由空间微分来实现锐化处理，微分算子的响应强度与图像在用算子操作的这一点的突变程度成正比，图像微分会增强边缘和噪声，削弱灰度变换缓慢的区域。

3.6.1 一阶微分滤波器

定义为$\frac{\alpha f}{\alpha x}$=f(x+1)-f(x),在不平坦的区域一阶微分不为零。二阶微分定义$\frac{{\alpha }^{2}f}{\alpha x^2}$=f(x+1)+f(x-1)-2f(x),除梯度或斜坡起始点外的区域值为零。

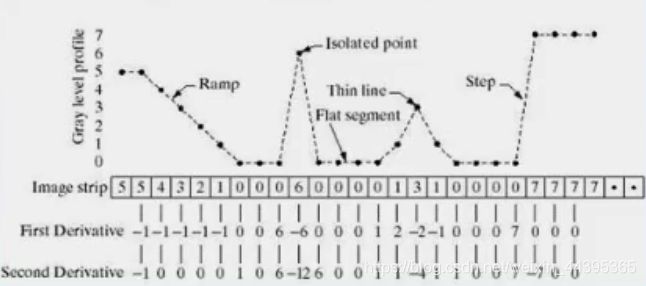
一阶微分在边缘会产生较粗的边缘，二阶微分产生由零分开的一个像素宽的双边缘，在增强细节方面比一阶微分好得多。

3.6.2 基于拉普拉斯算子的二阶微分滤波器

定义为${\nabla }^2$f=$\frac{{\alpha }^{2}f}{\alpha x^2}$+$\frac{{\alpha }^{2}f}{\alpha y^2}$，拉普拉斯变换也是一个线性分子，x方向上：$\frac{{\alpha }^{2}f}{\alpha x^2}$=f(x+1，y)+f(x-1,y)-2f(x,y),y方向上类似。
二维：${\nabla }^2$f（x,y）=f(x+1,y)+f(x-1,y)+f(x,y+1)+f(x,y-1)-4f(x,y)
滤波器响应与图像突变方向无关,求二阶导的方法，即横轴两侧像素值相加-中间像素值×2、纵轴上下像素值相加-中间像素值×2


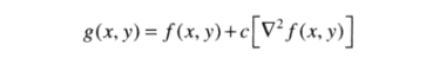
g(x,y)为锐化过的图像，若为上图的a,b,为锐化边缘，令c为-1,如a图，g（x,y）=-4+(4+16)*(-1)=-24,差值为20；c,d图情况，令c为1。

总结

灰度变换引入在空间域内领域处理的概念和映射关系，提供若干个函数处理图像的对比度和轮廓，并引入直方图均衡和匹配的概念，引入直方图能够很好得获取图像的信息；空间滤波主要介绍了一系列的滤波器，滤波器的功能主要是处理像素点，滤波器分为平滑和锐化两种，前者运用了卷积和离散积分的概念，后者运用了微分的概念，分别用于模糊和锐化的情况。