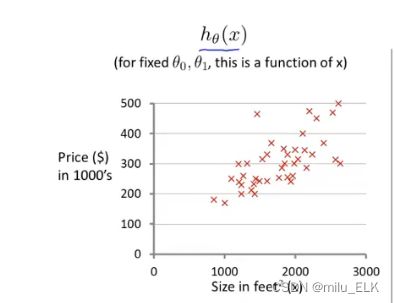
【机器学习】线性回归与代价函数

上一章——监督学习与无监督学习

---

模型描述

回到上一章的第一个例子，依旧是卖房子

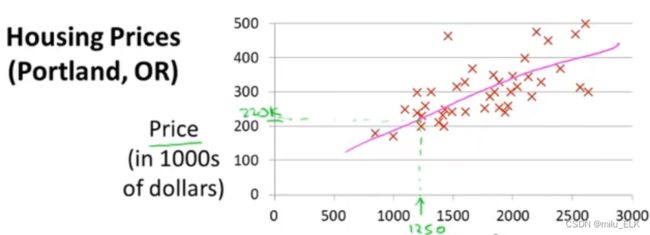
所有的数据点都拥有Price和Size两个属性/特征,我们根据它的属性制作了一个数据表

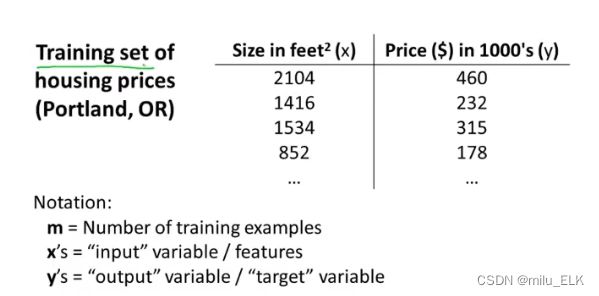
我们将上面这些数据的集合称之为数据集,而若用它来进行机器学习训练便称其为训练集
而机器学习的目的就是通过给出的训练集来学习如何预测房价
其中m代表训练集的数据量
x代表训练集的输入的特征
y代表训练集的输出的目标变量
用($x^{(i)},y^{(i)})$来表示对应的元素，其中i为行索引标号
如($x^{(1)},y^{(1)})$为（2104，460）

一个简单的机器学习流程图如下：

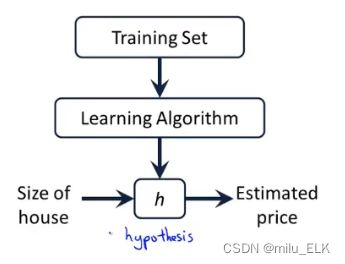
对于学习算法，我们给出一个训练集，用这个训练集来构建假设函数h，最终向h输入自变量x，就可以得到目标变量y

---

线性回归

在这个图片中，我们画出了一条直线来进行拟合，虽然不太准确，不过一条直线是最简单的拟合方式
也就是说我们的假设函数h是一条线性函数，即h=ax+b的形式，我们用θ来表示其中的系数
线性假设方程:$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$

很显然并不是所有点都会落到我们要找的线性方程上，但是我们可以找到一个最合适的线性方程
而判断这个线性方程是否最合适，我们需要用到最小二乘法,借用其他博主的描述:

最小二乘法

————————————————
最小二乘法（又称最小平方法）是一种数学优化技术。它通过最小化误差（真实目标对象与拟合目标对象的差）的平方和寻找数据的最佳函数匹配。利用最小二乘法可以简便地求得未知的数据，并使得这些求得的数据与实际数据之间误差的平方和为最小。

• 最小二乘法还可用于曲线拟合。对于平面中的这n个点，可以使用无数条曲线来拟合。要求样本回归函数尽可能好地拟合这组值。综合起来看，这条直线处于样本数据的中心位置最合理。
  选择最佳拟合曲线的标准可以确定为：使总的拟合误差（即总残差）达到最小
• 最小二乘法也是一种优化方法，求得目标函数的最优值。并且也可以用于曲线拟合，来解决回归问题。回归学习最常用的损失函数是平方损失函数，在此情况下，回归问题可以著名的最小二乘法来解决。

简而言之，最小二乘法同梯度下降类似，都是一种求解无约束最优化问题的常用方法，并且也可以用于曲线拟合，来解决回归问题。
————————————————
【版权声明：本文为CSDN博主「THE@JOKER」的原创文章，遵循CC 4.0 BY-SA版权协议，转载请附上原文出处链接及本声明。
原文链接：https://blog.csdn.net/W1995S/article/details/118153146】
————————————————

下面给出最小二乘法求θ的公式:
$\underset{{\theta }_0,{\theta }_1}{\min }\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$
即最终的${\theta }_0,{\theta }_1$的值使得最小二乘法的结果和最小
其中线性假设方程:$h_{\theta }(x)={\theta }_0+{\theta }_{1}x$
为了方便，我们将其定义为关于${\theta }_0,{\theta }_1$的代价函数$J$,
$J({\theta }_0,{\theta }_1)=\frac{1}{2m}\sum _{i=1}^m(h_{\theta }(x^{(i)})-y^{(i)}{)}^2$
其中乘以$\frac{1}{2m}$是为了使数据标准化来方便图像处理的，
由于回归算法的算术复杂度是$O(n^3)$,因此数据范围不能太大，需要通过标准化数据来控制大小

.
最终得到简化的公式：
$\underset{{\theta }_0,{\theta }_1}{\min }J({\theta }_0,{\theta }_1)$

---

代价函数与假设函数

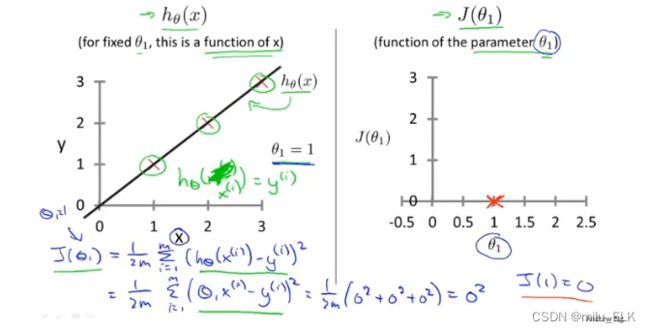
当我们的假设函数$h$如左图所示，此时${\theta }_0=0,{\theta }_1=1$完美拟合了给出的三个点，显然$h$是一条经过原点的直线
那么作出以${\theta }_1$为横轴，$J({\theta }_0,{\theta }_1)$为纵轴的代价函数$J$的图像，用红X标出结果
同理改变$\theta$值作出其他图像

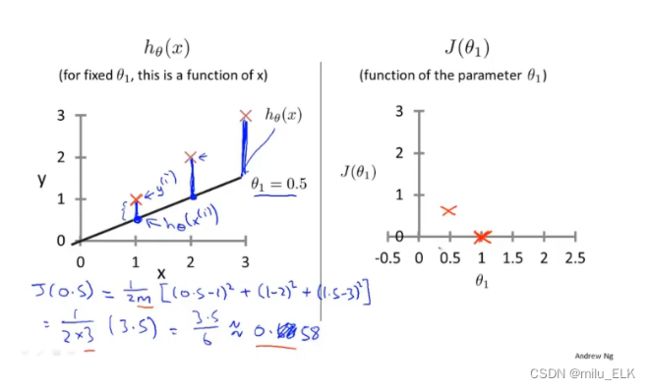
如果你改变的次数足够多，用描点法会发现当${\theta }_0=0$时$J({\theta }_1)$的图像类似于开口向上的二次函数

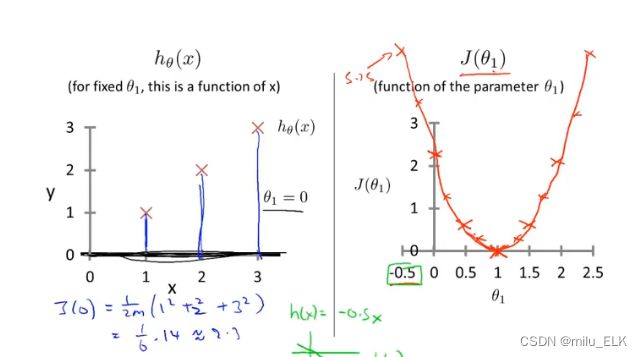
而最佳的位置当然是全部拟合的那幅图，对应的位置是图中二次函数的最低点
因此，实际上机器学习的目的就是找到这个代价函数的最低点
在上述例子中我们将${\theta }_0=0$作为定值，而如果其也作为变量的话，我们会得到一个三维图

比如对于这个训练集，我们得到的三维代价函数图是这样的

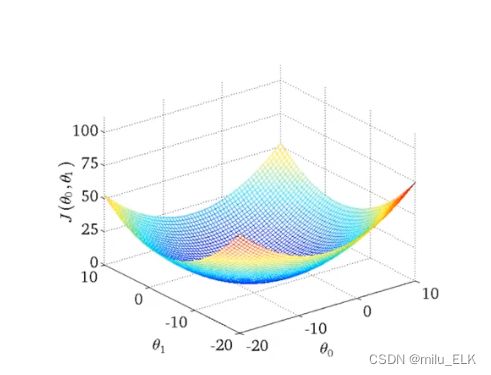
可以看到这是一个碗形图，那么最佳代价函数的位置当然是处于碗底的那个点，如何去找到这个点呢？
虽然我们难以直观地看到三维图像，但是我们可以使用等高线图将其平铺到二维

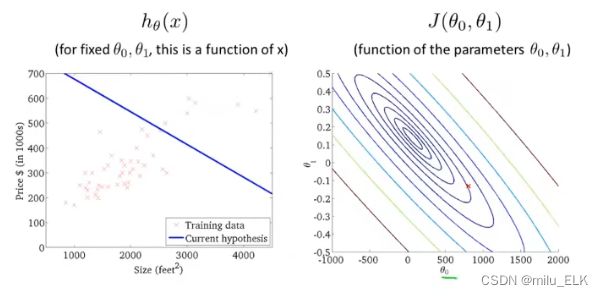
在上面这个等高线图中，越往内越接近图像的最低点，这样就能直观地找到该点对应的$\theta$值

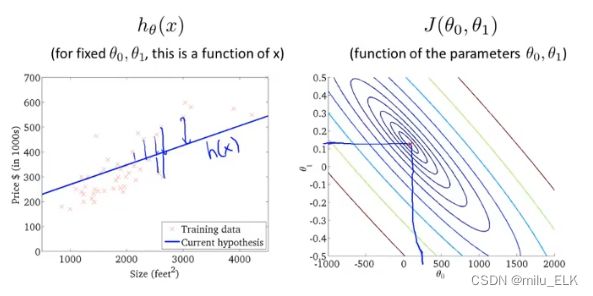
最终我们找到了这个点，使得假设函数中各离散点到拟合直线的距离差的平方之和最小，则此时所取的$\theta$即为最佳的系数。

---

下一章——梯度下降