Python金融学基础——夏普比率(Sharpe-ratio)和资产组合价值(portfolio-value)
前面的课程主要是在研究Pandas的时序分析实现,以及利用statsmodel对时序数据进行ARIMA以及有权重的ARIMA模型的建模,并尝试预测未来的走向。从这节课开始,我们正式进入Python金融学基础,会介绍一些金融学的概念和实现方法。
本节课主要以苹果、亚马逊、IBM、思科以及沃尔玛的股票市场价格为原始数据,分析这几只股票的资产组合的计算方式和夏普比率的计算,其中会涉及到日收益率、累积收益率的计算等等。
本文主要流程:
一、基本概念
1.1 资产组合
我们的资产往往不是单一的,我们会同时购买好几支股票或者基金,这样总资产的收益其实是每个资产的按照比例的权重加和结果,并且如果购买的资产之间具有对冲,我们还能够利用这点来降低风险,减少总资产损失的不确定性。比如王婆一个儿子卖伞和一个儿子卖鞋的故事就是这样,只要天放晴,卖鞋儿子生意好,但是伞卖不出去;同理,天下雨的时候卖伞的儿子生意好,鞋子卖不出去。其实天气就是波动,或说在这里就是风险,但是王婆家两个儿子卖的东西其实有对冲的作用,也就是不管是天晴天阴,家里都会有生意,因此就降低了风险可能带来的损失。这就是一个资产组合。
1.2 夏普比率
夏普指数是一个用于计算根据风险调整过的回报率的测量指标,说白了,就是说我们只要做投资,就肯定会有风险,但在相同的回报率下,风险有可能不一样,正常人在这个时候肯定都会选择风险小的,那么我们需要一个指标来评判在相同单位风险上,哪个收益大?或者说在收益相同的情况下,哪些风险不必要冒?所以夏普比率相当于是用风险把收益率给平均化了,放到太阳底下去看看每份相同的风险下收益率的大小是多少。
计算公式如下:
Sharpe Ratio=(Mean of portfolio return - Risk-free return) / standard deviation of portfolio return
这个公式Mean of portfolio return就是投资组合的收益率的平均值,risk-free return就是当地没有风险的回报率,也就是放在银行当中的回报率,比如美国的银行利率就接近于0,standard deviation of portfolio return就是投资组合的收益率的标准偏差。
以上是原始的夏普比率的计算方法,实际上对于固定时间内的夏普比率还得乘上一个k值。
对于不同采样频率的k值情况:
- Daily=sqrt(252)(最小粒度是按天计)
- Weekly=sqrt(52)(最小粒度是按星期计)
- Monthly=sqrt(12)(最小粒度是按月计)
年利率和日利率的转换:
二、读取数据
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
#%matplotlib inline
aapl=pd.read_csv('AAPL_CLOSE',index_col='Date',parse_dates=True)
cisco=pd.read_csv('CISCO_CLOSE',index_col='Date',parse_dates=True)
ibm=pd.read_csv('IBM_CLOSE',index_col='Date',parse_dates=True)
amzn=pd.read_csv('AMZN_CLOSE',index_col='Date',parse_dates=True)2.1 归一化收盘价格
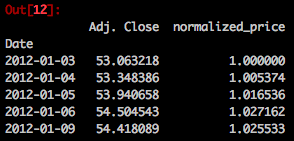
也就是求每天的收盘价格相对于初始第一天的价格的百分率。
for stock in [aapl, cisco, ibm, amzn]:
stock['normalized_price']=stock['Adj. Close']/stock['Adj. Close'].iloc[0]
aapl.head()2.2 资产分配
现在假定我们四种股票都买了,并且是按照一定的权重去买,现在我们需要计算一下每天的收益率总和。
- 30% in Apple
- 20% in Google/Alphabet
- 40% in Amazon
- 10% in IBM
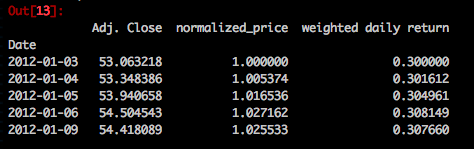
做法是把每只股票的收益率乘以对应的权重,把所有经过权重相乘后的收益率之和加起来就是总的收益率。
for stock, weight in zip([aapl, cisco, ibm, amzn],[0.3, 0.2, 0.1, 0.4]):
stock['weighted daily return']=stock['normalized_price']*weight
aapl.head()大概可以了,然后我们把对应的经过权重计算的归一日回报率全部都整合到一张表当中。
total_stock=pd.concat([aapl['weighted daily return'], cisco['weighted daily return'], ibm['weighted daily return'], amzn['weighted daily return']],axis=1)
total_stock.columns=['aapl', 'cisco', 'ibm', 'amzn']
total_stock.head()2.2 投资
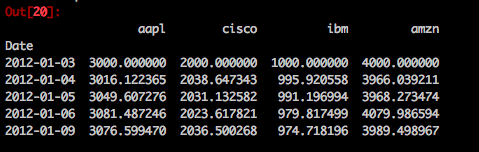
然后假设我们投资10000元,那么就在上面回报率的基础上乘以10000。
total_invest=total_stock*10000
total_invest.head()total_invest['Total Pos']=total_invest.sum(axis=1)
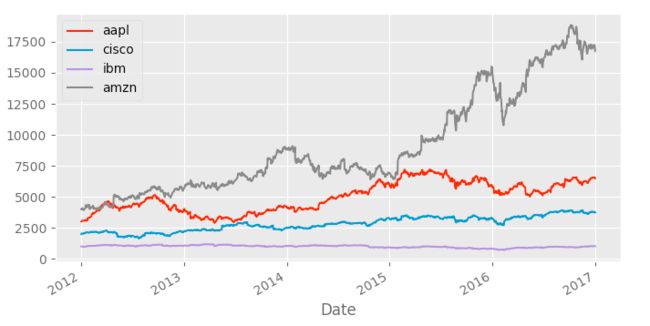
total_invest.head()然后我们绘制下每天的总收益.
plt.style.use('ggplot')
total_invest['Total Pos'].plot(label='Total Pos')
plt.legend(loc='best')
plt.title('Total Portfolio Value')我们绘制一下除了总资产以外的其他单只股票的收益情况
total_invest.drop('Total Pos',axis=1).plot(figsize=(8,4))三、资产的统计学值
3.1 日回报率
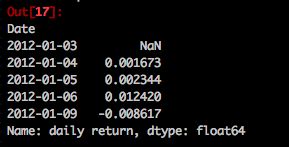
total_invest['daily return']=total_invest['Total Pos'].pct_change(1)
total_invest['daily return'].head()3.2 累积回报率
计算方法是最后一天与一开始第一天的变化百分比,相当于是增加了多少百分比。
cumulative_return=total_invest['Total Pos'].iloc[-1]/total_invest['Total Pos'].iloc[0]-1
print cumulative_return3.3 平均日回报率
也就是对日回报率做平均计算
total_invest['daily return'].mean()3.4 日回报率的标准差
total_invest['daily return'].std()total_invest['daily return'].plot(kind='kde')四、夏普比率
接下来我们计算一下总资产的夏普比率,也就是拿总资产日回报率的均值除以日回报率的标准差。之后由于我们这里的粒度是以天算的,所以要乘以sqrt(252),252代表252天
SR=total_invest['daily return'].mean()/total_invest['daily return'].std()
SRimport numpy as np
ASR=np.sqrt(252)*SR
ASR最后我们绘制一下各个股票的收盘价分布情况
for stock in [aapl, cisco, ibm, amzn]:
stock['Adj. Close'].pct_change(1).plot(kind='kde')